Low-Pressure Small MEMS Accelerometer Using Sigma-Delta Modulation †
Abstract
:1. Introduction
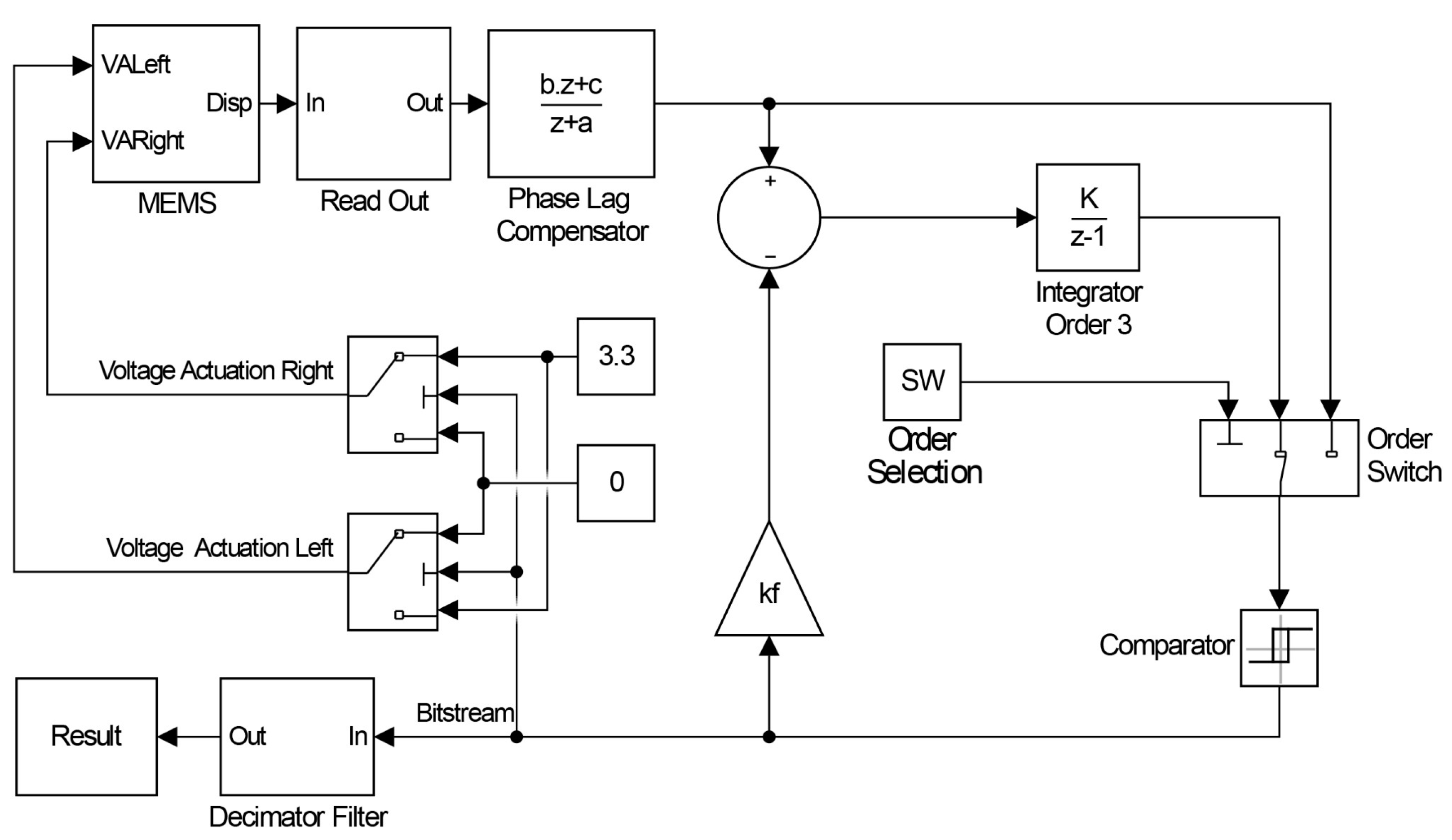
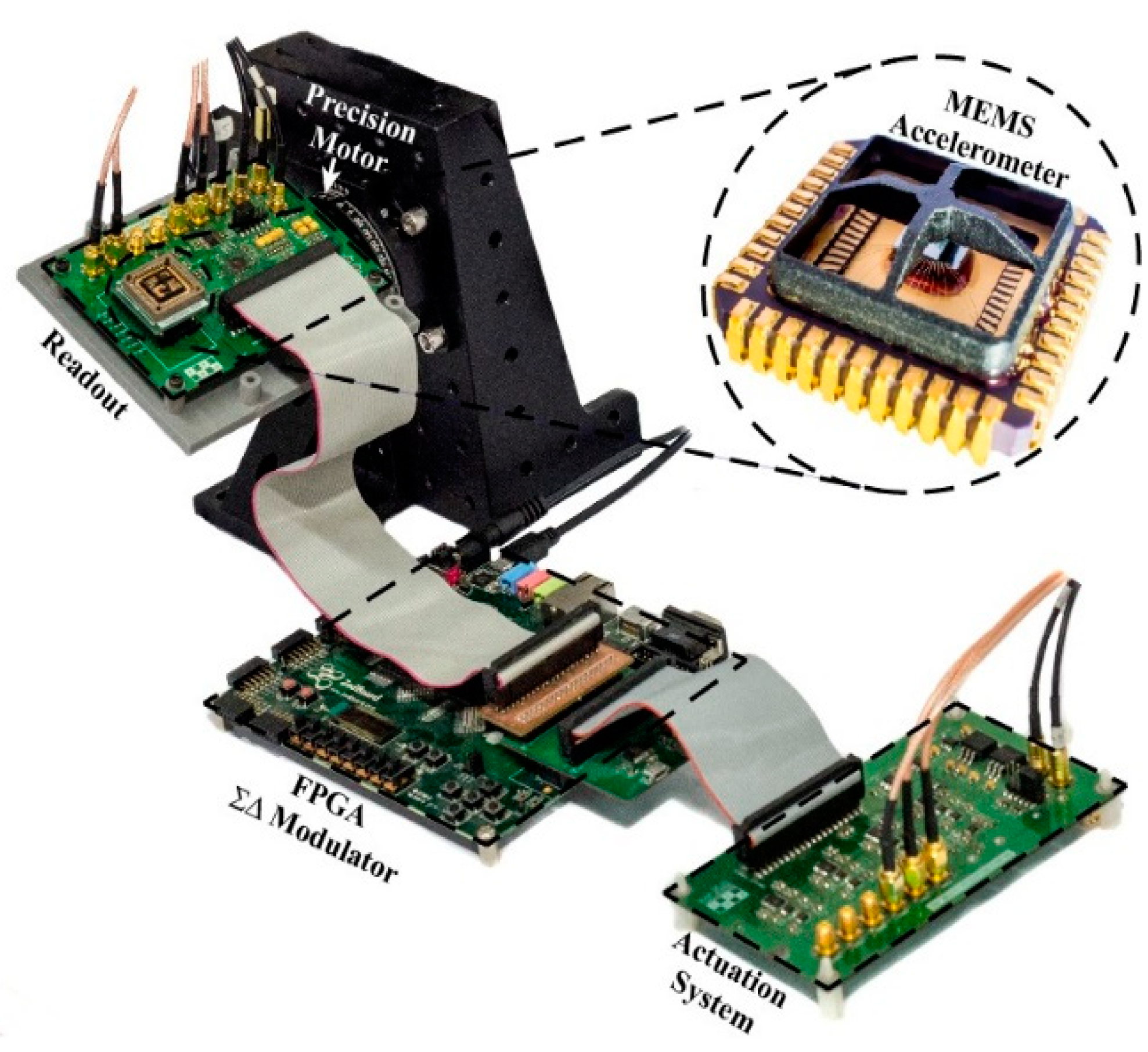
2. System Design
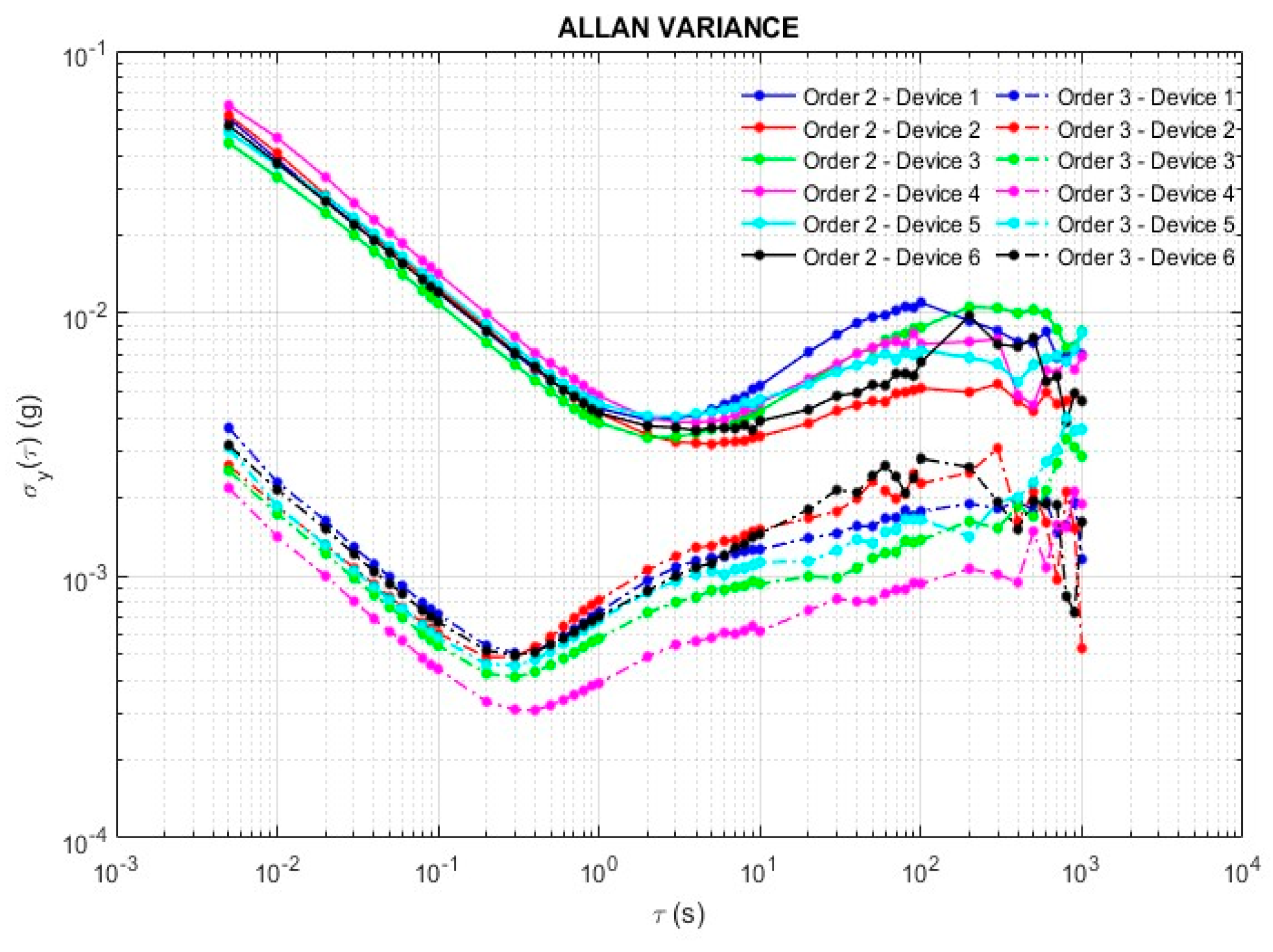
3. Results
4. Conclusions and Future Work
Acknowledgments
References
- Chen, F.; Yuan, W.; Chang, H.; Zeimpekis, I.; Kraft, M. Low noise vacuum MEMS closed-loop accelerometer using sixth-order multi-feedback loops and local resonator sigma delta modulator. In Proceedings of the IEEE 27th International Conference on Micro Electro Mechanical Systems (MEMS), San Francisco, CA, USA, 26–30 January 2014; pp. 761–764. [Google Scholar]
- Amini, B.V.; Abdolvand, R.; Ayazi, F. A 4.5-mW Closed-Loop Δ∑ Micro-Gravity CMOS SOI Accelerometer. IEEE J. Solid-State Circuits 2006, 41, 2983–2991. [Google Scholar] [CrossRef]
- Xu, H.; Liu, X.; Yin, L. A Closed-Loop ∑Δ Interface for a High-Q Micromechanical Capacitive Accelerometer with 200 ng/√Hz Input Noise Density. IEEE J. Solid-State Circuits 2015, 50, 2101–2112. [Google Scholar] [CrossRef]
- Inose, H.; Yasuda, Y.; Murakami, J. A Telemetering System by Code Modulation—Δ-Σ Modulation. IRE Trans. Space Electron. Telem. 1962, SET-8, 204–209. [Google Scholar] [CrossRef]
- Zwahlen, P.; Dong, Y.; Nguyen, A.M.; Rudolf, F.; Stauffer, J.M. Breakthrough in high performance inertial navigation grade Sigma-Delta MEMS accelerometer. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Myrtle Beach, SC, USA, 23–26 April 2012; Volume 37, pp. 15–19. [Google Scholar]
- Wilcock, R.; Kraft, M. Genetic Algorithm for the Design of Electro-Mechanical Sigma Delta Modulator MEMS Sensors. Sensors 2011, 11, 9217–9232. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Kazmierski, T.J. An automated design flow for MEMS accelerometers with Sigma-Delta control. In Proceedings of the IEEE International Conference on Information and Automation, Harbin, China, 20–23 June 2010; pp. 559–564. [Google Scholar]
- Dong, Y.; Zwahlen, P.; Nguyen, A.M.; Frosio, R.; Rudolf, F. Ultra-high precision MEMS accelerometer. In Proceedings of the 16th International Solid-State Sensors, Actuators and Microsystems Conference, Beijing, China, 5–9 June 2011; pp. 695–698. [Google Scholar]
- Lemkin, M.; Boser, B.E. A three-axis micromachined accelerometer with a CMOS position-sense interface and digital offset-trim electronics. IEEE J. Solid-State Circuits 1999, 34, 456–468. [Google Scholar] [CrossRef]
- Nakamura, S. MEMS Inertial Sensor Toward Higher Accuracy & Multi-Axis Sensing. In Proceedings of the IEEE Sensors, 31 October–3 November 2005; pp. 939–942. [Google Scholar]
- Henrion, W.; DiSanza, L.; Ip, M.; Terry, S.; Jerman, H. Wide dynamic range direct digital accelerometer. In Proceedings of the IEEE 4th Technical Digest on Solid-State Sensor and Actuator Workshop, Hilton Head Island, SC, USA, 4–7 June 1990; pp. 153–157. [Google Scholar]
- Sonmez, U.; Kulah, H.; Akin, T. A fourth order unconstrained Δ∑ capacitive accelerometer. In Proceedings of the 16th International Solid-State Sensors, Actuators and Microsystems Conference, Beijing, China, 5–9 June 2011; pp. 707–710. [Google Scholar]
- Messner, W. Formulas for asymmetric lead and lag compensators. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 3769–3774. [Google Scholar]
- Dong, Y.; Kraft, M.; Redman-White, W. Higher order noise-shaping filters for high-performance micromachined accelerometers. IEEE Trans. Instrum. Meas. 2007, 56, 1666–1674. [Google Scholar] [CrossRef]


| Pull-in Voltage (V) | Pull-in Voltage Error (%) | Resonant Frequency (Hz) | Resonant Frequency Error (%) | Quality Factor | Quality Factor Error (%) | |
|---|---|---|---|---|---|---|
| Theorectical | 1.962 | - | 2591 | - | 58.6 | - |
| Device 1 | 1.910 | 2.7 | 2498 | 3.6 | 61.1 | 4.3 |
| Device 2 | 1.839 | 3.5 | 2535 | 2.2 | 58.3 | 0.5 |
| Device 3 | 1.892 | 3.6 | 2537 | 2.1 | 56.0 | 4.4 |
| Device 4 | 1.893 | 3.5 | 2543 | 1.9 | 53.9 | 8.0 |
| Device 5 | 1.888 | 3.8 | 2526 | 2.5 | 61.4 | 4.8 |
| Device 6 | 1.888 | 3.8 | 2536 | 2.1 | 58.6 | 0.0 |
| Sensitivity (bit/g) | ||
|---|---|---|
| Order 2 | Order 3 | |
| Device 1 | 14.511 | 13.640 |
| Device 2 | 14.437 | 13.543 |
| Device 3 | 14.463 | 13.690 |
| Device 4 | 14.330 | 13.760 |
| Device 5 | 14.353 | 13.651 |
| Device 6 | 14.496 | 13.502 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lima, V.; Cabral, J.; Kuhlmann, B.; Rocha, L.A. Low-Pressure Small MEMS Accelerometer Using Sigma-Delta Modulation. Proceedings 2018, 2, 1029. https://doi.org/10.3390/proceedings2131029
Lima V, Cabral J, Kuhlmann B, Rocha LA. Low-Pressure Small MEMS Accelerometer Using Sigma-Delta Modulation. Proceedings. 2018; 2(13):1029. https://doi.org/10.3390/proceedings2131029
Chicago/Turabian StyleLima, Vasco, Jorge Cabral, Burkhard Kuhlmann, and Luis Alexandre Rocha. 2018. "Low-Pressure Small MEMS Accelerometer Using Sigma-Delta Modulation" Proceedings 2, no. 13: 1029. https://doi.org/10.3390/proceedings2131029
APA StyleLima, V., Cabral, J., Kuhlmann, B., & Rocha, L. A. (2018). Low-Pressure Small MEMS Accelerometer Using Sigma-Delta Modulation. Proceedings, 2(13), 1029. https://doi.org/10.3390/proceedings2131029






