Noise Characterization of Vortex-State GMR Sensors with Different Free Layer Thicknesses †
Abstract
:1. Introduction
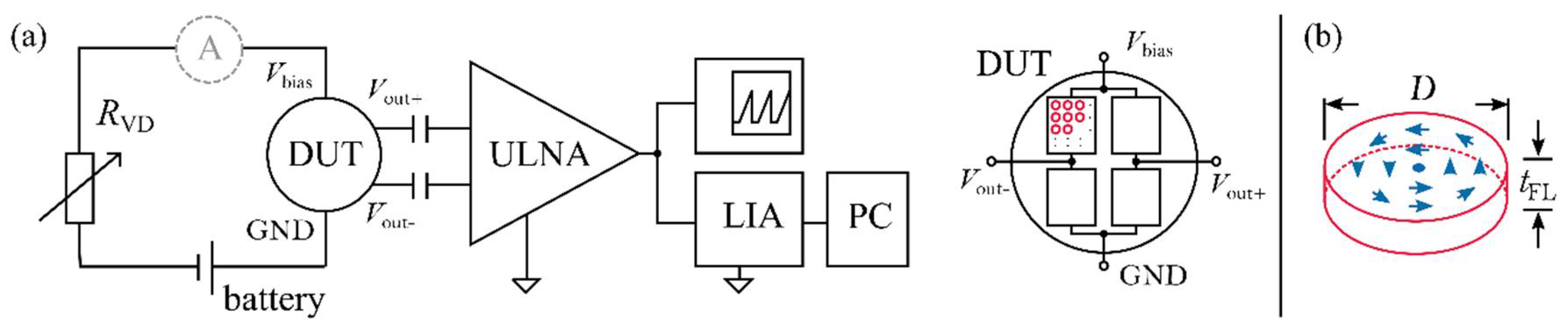
2. Materials and Methods
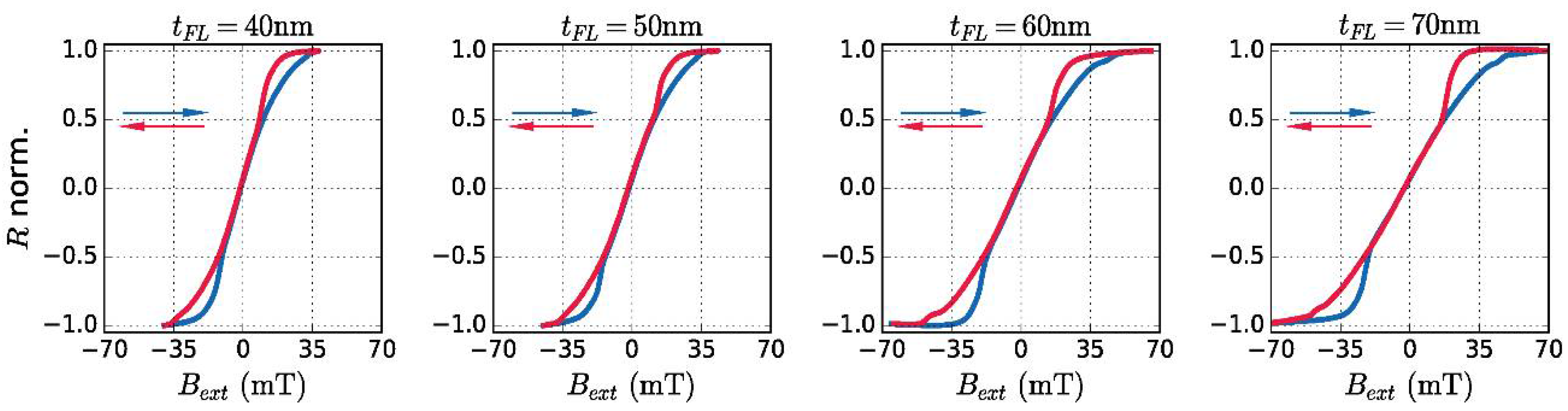
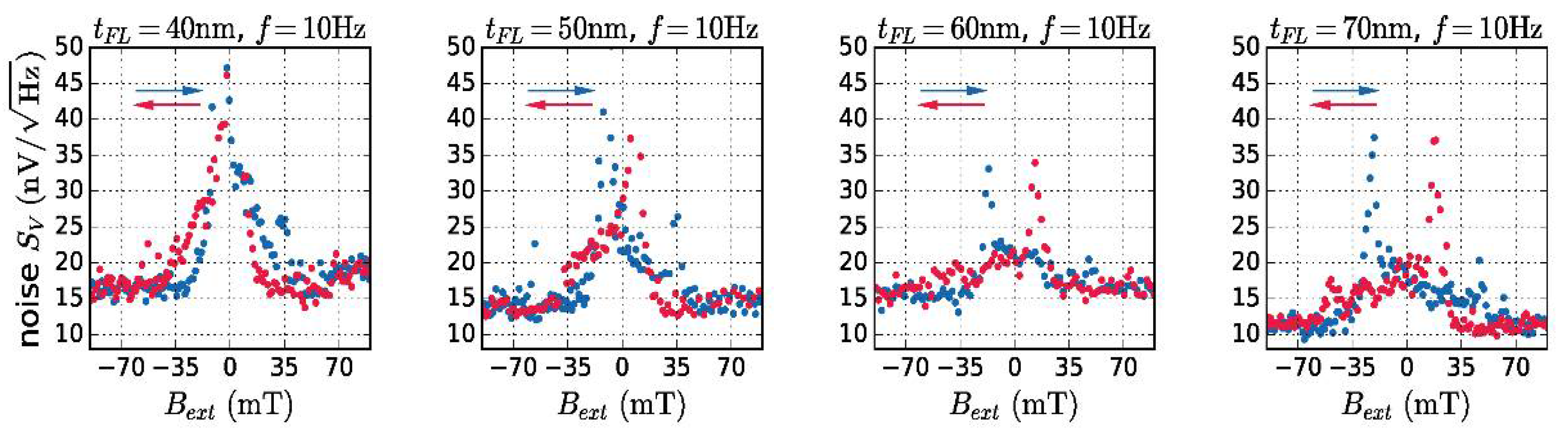
3. Results
4. Discussion
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Zimmer, J.; Satz, A.; Raberg, W.; Brueckl, H.; Suess, D. Device, Magnetic Sensor Device and Method. USA U.S. Application 20150185297A1, 2 July 2015. [Google Scholar]
- Wurft, T.; Raberg, W.; Pruegl, K.; Satz, A.; Reiss, G.; Brueckl, H. The Influence of Edge Inhomogeneities on Vortex Hysteresis Curves in Magnetic Tunnel Junctions. IEEE Trans. Magn. 2017, PP, 1. [Google Scholar] [CrossRef]
- Suess, D.; Bachleitner-Hofmann, A.; Satz, A.; Weitensfelder, H.; Vogler, C.; Bruckner, F.; Abert, C.; Prügl, K.; Zimmer, J.; Huber, C.; et al. Topologically protected vortex structures for low-noise magnetic sensors with high linear range. Nat. Electron. 2018, 1, 362–370. [Google Scholar] [CrossRef]
- Scandurra, G.; Cannat, G.; Ciofi, C. Differential ultra low noise amplifier for low frequency noise 77 measurements. AIP Adv. 2011, 1, 022144. [Google Scholar] [CrossRef]
- Hooge, F.N. 1/f noise sources. IEEE Trans. Electron. Devices 1994, 41, 1926–1935. [Google Scholar] [CrossRef]
- Reig, C.; Cardoso, S.; Mukhopadhyay, S.C. Giant Magnetoresistance (GMR) Sensors: From Basis to State-of-the-Art Applications; Springer-Verlag: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Egelhoff, W.; Pong, P.; Unguris, J.; McMichael, R.; Nowak, E.; Edelstein, A.; Burnette, J.; Fischer, G. Critical challenges for picoTesla magnetic-tunnel-junction sensors. Sens. Actuators A Phys. 2009, 155, 217–225. [Google Scholar] [CrossRef]
- Stutzke, N.A.; Russek, S.E.; Pappas, D.P.; Tondra, M. Low-frequency noise measurements on commercial magnetoresistive magnetic field sensors. J. Appl. Phys. 2005, 97, 10Q107. [Google Scholar] [CrossRef]
- Guslienko, K.Y.; Novosad, V.; Otani, Y.; Shima, H.; Fukamichi, K. Field evolution of magnetic vortex state in ferromagnetic disks. Appl. Phys. Lett. 2001, 78, 3848–3850. [Google Scholar] [CrossRef]
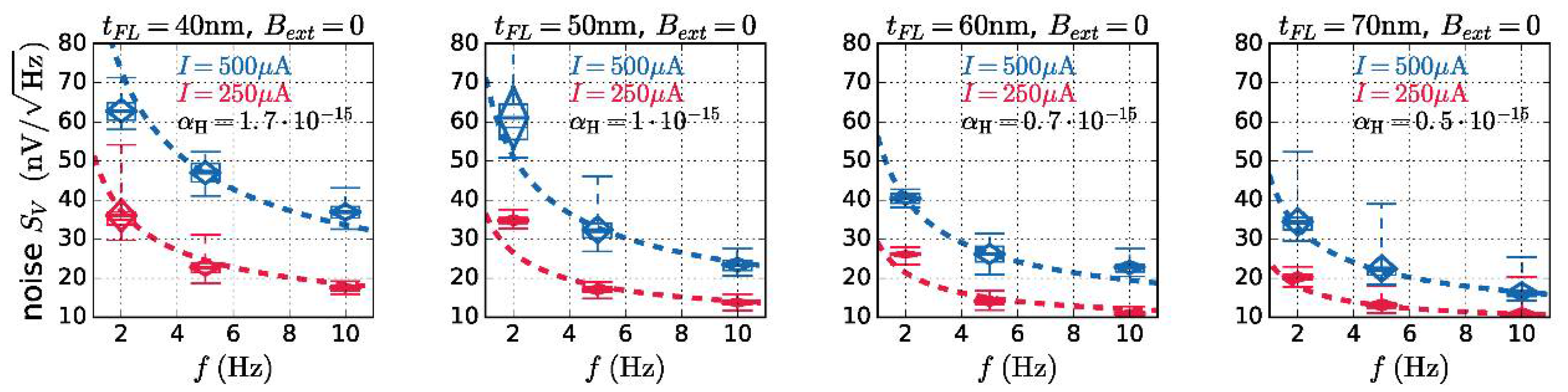
| Thickness tFL [nm] | Noise Parameter αH | Magnetic Contribution αH,mag |
|---|---|---|
| 40 | 1.7 · 10−15 | αH,mag = 0.83 · αH |
| 50 | 1.0 · 10−15 | αH,mag = 0.76 · αH |
| 60 | 0.7 · 10−15 | αH,mag = 0.63 · αH |
| 70 | 0.5 · 10−15 | αH,mag = 0.57 · αH |
| Thickness | Diameter | Resistance | MR Ratio | Sensitivity | Detectivity |
|---|---|---|---|---|---|
| tFL [nm] | D [µm] | R0(B = 0)[Ω] | MR[%] | S[%/mT] | ]@10 Hz |
| 40 | 2 | 4972 | 5.87 | 0.141 | 29.3 |
| 50 | 2 | 4504 | 5.52 | 0.113 | 28.2 |
| 60 | 2 | 4228 | 5.18 | 0.076 | 35.2 |
| 70 | 2 | 4058 | 4.68 | 0.063 | 36.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weitensfelder, H.; Brueckl, H.; Satz, A.; Suess, D. Noise Characterization of Vortex-State GMR Sensors with Different Free Layer Thicknesses. Proceedings 2018, 2, 1013. https://doi.org/10.3390/proceedings2131013
Weitensfelder H, Brueckl H, Satz A, Suess D. Noise Characterization of Vortex-State GMR Sensors with Different Free Layer Thicknesses. Proceedings. 2018; 2(13):1013. https://doi.org/10.3390/proceedings2131013
Chicago/Turabian StyleWeitensfelder, Herbert, Hubert Brueckl, Armin Satz, and Dieter Suess. 2018. "Noise Characterization of Vortex-State GMR Sensors with Different Free Layer Thicknesses" Proceedings 2, no. 13: 1013. https://doi.org/10.3390/proceedings2131013
APA StyleWeitensfelder, H., Brueckl, H., Satz, A., & Suess, D. (2018). Noise Characterization of Vortex-State GMR Sensors with Different Free Layer Thicknesses. Proceedings, 2(13), 1013. https://doi.org/10.3390/proceedings2131013




