Carbon Dioxide Emissions from a Ground Heat Pump for a Detached House ^†

Abstract

Inasmuch as the European Union promotes only energetically viable heat pumps in a given location, the aim of the work is an assessment of whether a ground-to-water heat pump (ground source heat pump: GSHP) can be considered as an ecological heat generator in Polish climatic conditions and those of the energy market. Here, as an estimator, the net seasonal coefficient of performance (SCOP_net) was selected. Estimation was done using 10-year temperature measurements. It was found that in heating mode SCOP_net value equaled 4.83, satisfying European Commission guidelines. According to the guidelines, the minimal SCOP_net value in Polish energy market conditions should exceed 3.5. CO₂ emissions from the GSHP represented two-thirds of CO₂ emissions of an air-to-water heat pump (air source heat pump: ASHP) in the same building. The ground heat pump thus meets the ecological heat generator conditions set by the European Commission.

1. Introduction

Increasing temperature, which has been observed for over a century, has led to international agreements such as the Kyoto Protocol and regulations such as European Union directives [1], where renewable energy sources (RES) are promoted. Heat pumps, which produce heat without the necessity for combustion of fossil fuels directly, represent an area of heat engineering. Generally, there are two low-temperature sources in the case of heat pumps: the Sun and the Earth’s inner core. Air-to-water heat pumps fail EU requirements [1] in Polish energy market conditions [2,3], due to too-low temperature values during the heating season. Since the temperature below the shallow zone is stable and at a sufficiently high level [4], the Earth’s inner core has higher energetic potential in a given location. Hence, the water-to-water heat pump satisfies EU requirements [5]. However, ground water basins are not ubiquitous. Thus, the purpose of the work is to assess whether ground-to-water heat pumps can be considered as ecological heat generators.

2. The Computation Algorithm

Only the heat pump, which produces significantly more heat than it uses with respect to primary energy to drive itself, is able to be promoted in European Economic Area states [1]. The best assessment factor seems to be SCOP_net, which in the case of Polish market conditions should be higher than 3.5 (cf. Rubik [6]). Here, an estimation is made for a case study of a building in which the design heat load is 11 kW, located in the fourth climate zone in Poland. It is based on temperature measurements carried out by the Institute of Meteorology and Water Management—National Research Institute (IMGW-PIB). The number of hours with each temperature value are counted in the 10 consecutive heating seasons. Then, the number of hours is converted to one Julian year (365.25 days) which is denoted as annus (abbr. “a”). The building is supplied with heat by the Vitocal 200-G, type 201.A13 heat pump manufactured by Viessmann (Allendorf, Germany) [1].

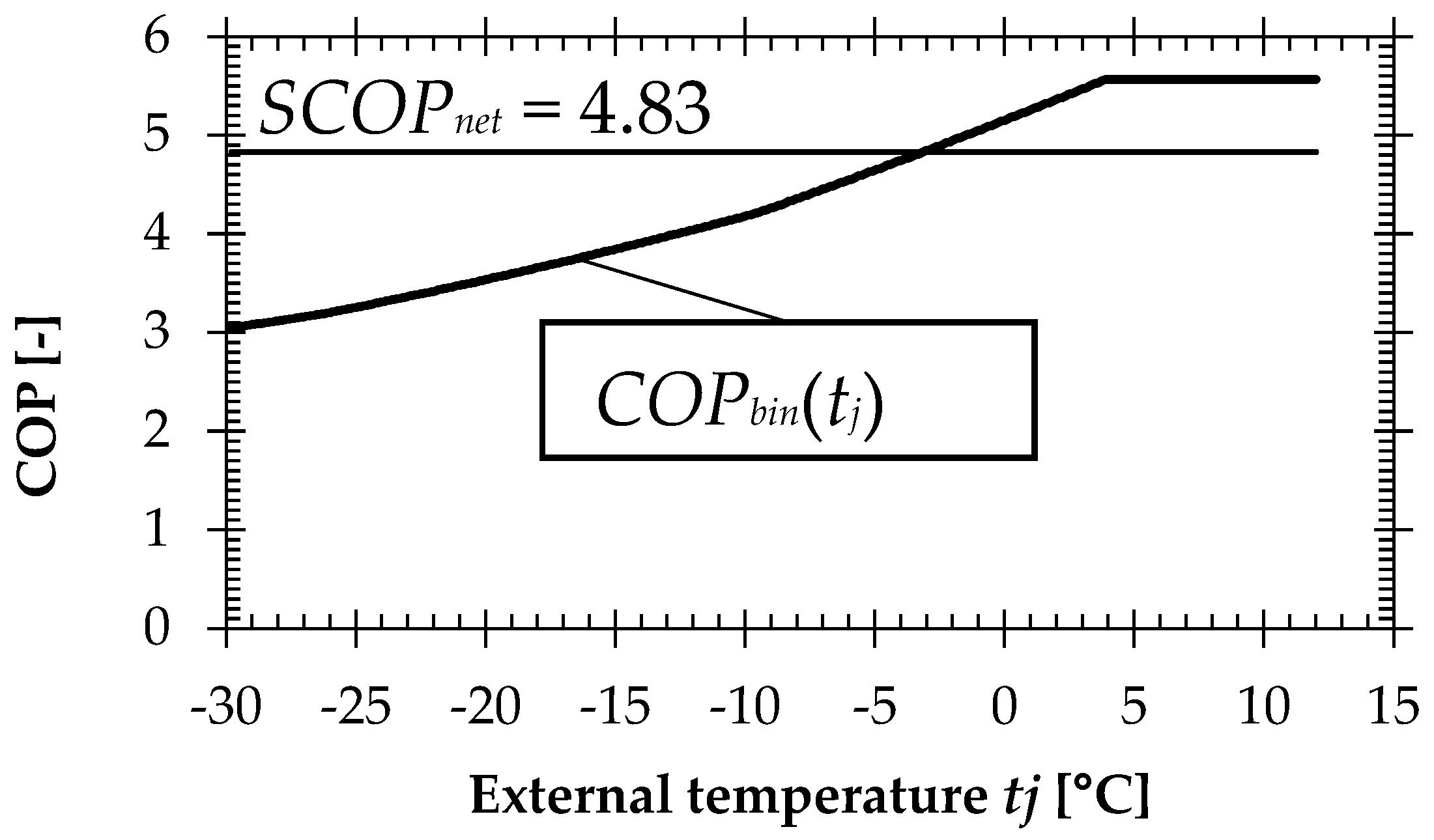
2.1. Seasonal Coefficient of Performance Determination

The calculations are performing using ground temperature determination, which is done using Baggs formula [7,8] after an adaptation to Polish climatic conditions made by Popiel et al. [9]:

$$t\left(z,\mathsf{\tau }\right)=\left(t_a+\Delta t_m\right)-1.07k_v{A}_s\exp \left(-0.00031552z{a}^{-0.5}\right)\cos \left[\frac{2\pi }{365}\left(\mathsf{\tau }-{\mathsf{\tau }}_o-0.018335z{a}^{-0.5}\right)\right]\left[°C\right]$$

(1)

where Δt_m is a difference between ground temperature below shallow zone and average annual air temperature, k_v is vegetation coefficient, A_s is the amplitude of annual air temperature, a is the soil thermal diffusivity, τ_o is the phase shift of the air temperature wave, and t_a is average annual air temperature.

Ground temperature was determined after integral averaging of Equation (1). Then, SCOP_net was determined in all the values of the outside temperature at which the device operates. This depends on the change of the outside air temperature and temperature of the low temperature source. Then, the part load for heating at each bin temperature value is fixed using the standard 14825:2016-08 [10]:

$$P_h\left(t_j\right)={\Phi }_i\frac{(t_i-t_j)}{(t_i-t_e)}[kW]$$

(2)

where Φ_i is total design heat loss obtained using an algorithm from PN-EN 12831 [11], t_i is the internal design temperature, assumed to be 20 °C, t_j is the external air temperature, and t_e is the external design temperature.

The value of SCOP_net is determined according to the standard EN 14825:2016 [10]:

$${SCOP}_{net}=\frac{\sum _{j=1}^n{h}_j\left[P_h\left(t_j\right)\right]}{\sum _{j=1}^n{h}_j[\frac{P_h\left(t_j\right)}{{COP}_{bin}\left(t_j\right)}]}[kW]$$

(3)

where h_j is number of bin hours occurring at external temperature t_j in the heating season, COP_bin(t_j) is the COP value of the unit at external temperature t_j (coefficient of performance at part load), and j is the number of a temperature value (the temperature values are sorted in ascending order).

2.2. Carbon Dioxide Emission Ascertainment

Carbon dioxide emissions are divided into direct and indirect emissions. The former originates from fuel combustion in a location when temperature is below a bivalent point, while the latter results from electricity generation for boiler system operation and heat production by heat pump at or above a bivalent point:

$$E_{}{}_{C{O}_2}={\displaystyle {\sum }_{j=0}^m{h}_j\left[\frac{{\mathsf{\beta }}_{gas}{P}_h\left(t_j\right)}{{\mathsf{\eta }}_b}+{\mathsf{\beta }}_{ag}{W}_{runj}\right]}+{\mathsf{\beta }}_{ag}{\displaystyle {\sum }_{j=m+1}^n{h}_j\left[\frac{P_h\left(t_j\right)}{CO{P}_{bin}\left(t_j\right)}\right]}\left[kgC{O}_2/a\right]$$

(4)

where β_gas represents the carbon dioxide emissions from natural gas combustion, W_run is the energy consumption for boiler system operation, β_ag is the aggregate carbon dioxide generation factor which accounts for direct and indirect emissions amid electrical energy production and considers shares of all the fuels in the Polish energy market (cf. PGE Obrót S.A. [12]), and m+1 is the number of t_j = −2.9 °C, the bivalent temperature when the air-to-water heat pump (ASHP) starts [2]. In the case of the ground-to-water heat pump (GSHP), m = 0, as the GSHP operates during the entire heating season and there is no bivalent heat generator; thus, the left summand in Equation (4) is equal to zero.

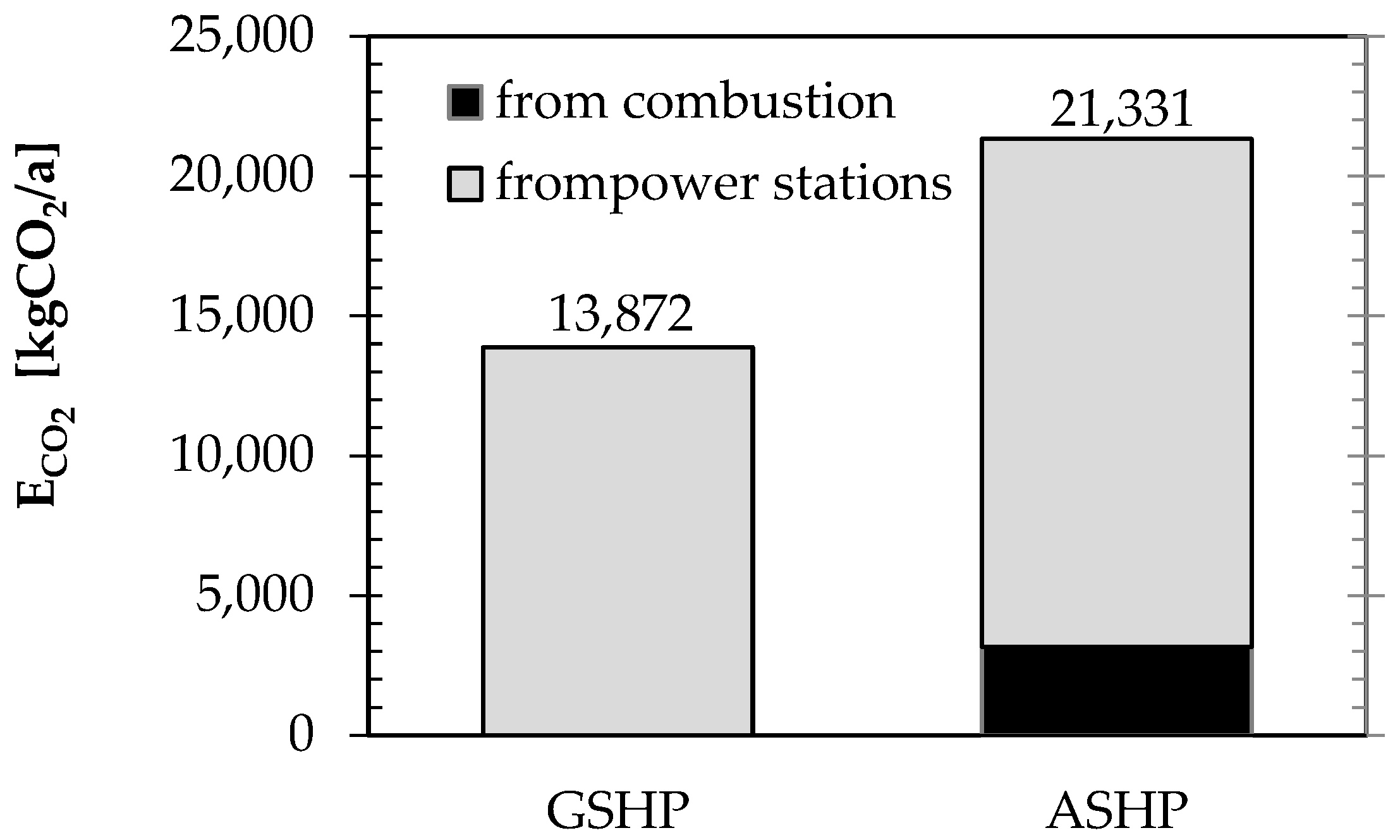
3. Results

COP_bin values increase from 3.05 at −29.8 °C (i.e., the lowest measured temperature during the 10-year period) to 5.57 at 12 °C when the heating system switches off. Here, SCOP_net = 4.83. COP_bin values at each bin temperature value of the analyzed device and the averaged value of the SCOP_net coefficient are presented in Figure 1.

Carbon dioxide emissions are calculated for GSHP and ASHP, as investigated earlier [2]. ASHP (SCOP_net = 2.55) had a condensed gas boiler as a bivalent heat generator [2]. Obtained emissions are plotted in Figure 2.

4. Discussion

The determined SCOP_net value satisfies the guidelines of the European Commission regarding heat pump type devices. According to the guidelines, the minimal SCOP_net value in Polish energy market conditions should be in excess of 3.5. In addition, it is seen that with the increase of outside temperature, the value of COP_bin increases. Moreover, a comparison between GSHP and ASHP, analyzed in an earlier paper [2], is made. The more efficient heat generator is the GSHP pump.

5. Conclusions

Taking into account the value of the energy efficiency coefficient, carbon dioxide emissions, and local climatic conditions, the ground heat pump meets the ecological heat generator conditions set by the European Commission. Thus, it can contribute to counteracting the intensification of the greenhouse effect phenomenon.