Determination of the In-Plane Thermal Diffusivity of Thin Film Based on the Periodic Regime of Local Heating ^†

1. Introduction

The in-plane thermal diffusivity of soft materials is critical for the development of functional thermal materials in nano/microscale integrated devices. Laser-induced localized periodic heating and imaging of spatially distributed periodic temperature responses are key techniques for determining in-plane thermophysical properties [1]. However, this method is significantly influenced by the three-dimensional geometry of the sample and the surface conditions (such as vacuum conditions). To avoid these multidimensional effects in thermal analysis, it is necessary to increase the frequency range of periodic heating as much as possible. This is typically limited by the frame rate of the imaging system.

In this study, we performed thermal imaging and analysis of periodic heating responses on the sample surface at frequencies far exceeding the frame rate of the imaging system. (Figure 1). The in-plane thermal diffusivity of thin polymer film was investigated by analyzing the in-plane periodic temperature response induced by a focused near-infrared laser (λ = 830 nm) in a broad frequency range exceeding the frame rate of an InSb infrared camera (sensitivity range 3 μm–5 μm).

2. Theory

The periodic temperature response at a single point on a sufficiently thin sample is described as follows.

$$T=T_0\mathit{sin}\left\{{\omega }_{1}t+∆\theta \left({\omega }_1\right)\right\}$$

(1)

Here, $T_0$ is the amplitude of temperature modulation, ${\omega }_1$ is the angular frequency of the temperature modulation, and $∆\theta \left({\omega }_1\right)$ is the phase delay due to in-plane thermal diffusion. Under the approximation of a thermally thick medium, the phase delay can be described as follows.

$$∆\theta \left({\omega }_1\right)=-\sqrt{{\displaystyle \frac{{\omega }_1}{2\alpha }}}d+\beta$$

(2)

The amplitude of the temperature modulation is typically sufficiently small to approximate the linear relationship between the signal intensity of the infrared camera and the temperature. The signal intensity of the temperature modulation measured in the mth image at the camera frame rate of $f_2$ can be described as follows.

$$\begin{array}{c}{I}_m=I_0\mathit{sin}\left\{2\pi {\displaystyle \frac{f_1}{f_2}}m+∆\theta \left({\omega }_1\right)\right\}\\ =I_0\mathit{sin}\left\{2\pi ∆f{\displaystyle \frac{m}{f_2}}+∆\theta \left({\omega }_1\right)\right\}\end{array}$$

(3)

Here, $m$ is the number of frames (integer), $f_1$ and $f_2$ represent the temperature modulation frequency and the image acquisition (frame rate) frequency, respectively, and $∆f$ is the difference frequency ($∆f=f_1-n{f}_2$), where n is the integer.

During the experiment, the frame rate of the infrared camera was fixed at $f_2= 80 \mathrm{H}\mathrm{z}$, and the difference frequencies of the acquired image series were also fixed $∆f= 1 \mathrm{H}\mathrm{z}$ by keeping relation of $∆f=f_1-n{f}_2$ and analyzed by Fourier-transform analysis.

3. Experimental Section

The schematic diagram of the focused laser-coupled thermal imaging system is depicted in Figure 1. The diode laser is mounted at diagonal angle to irradiate the sample from the side of the infrared camera (SC6000HS-MID-TH, FLIR Systems, Inc., Wilsonville, OR, USA) with a microscope. The spot size of the laser is approximately 1 μm, which is sufficiently smaller than the pixel size of the thermal imaging camera (3 μm). Therefore, in this study, it is reasonable to assume a single-pixel heating spot for data analysis, and it is also acceptable to ignore the minute extension of the heating spot along the tilt direction of the laser irradiation.

The sample (polymer thin film) was mounted on the hot stage with slide-in mechanics to the chamber. The main body of the chamber was cooled with water and the temperature of the hot stage was controlled using the thermocoupled reading placed near the sample position. The diode laser was driven by the function generator (Wave Factory 1942, NF Corporation, Yokohama, Japan), and the heating frequency was controlled between 0.1 Hz and 1 kHz.

The spatiotemporal temperature response to periodic laser heating on the surface of the sample was analyzed by Fourier-transforming the time dependence of the temperature distribution. The in-plane thermal diffusivity of the sample was analyzed by approximating the solution of the periodic regime heating as shown in Equation (2). This is applicable to the temperature response at a distance sufficiently far from the heating position with a sufficiently high heating frequency [2].

4. Results and Discussion

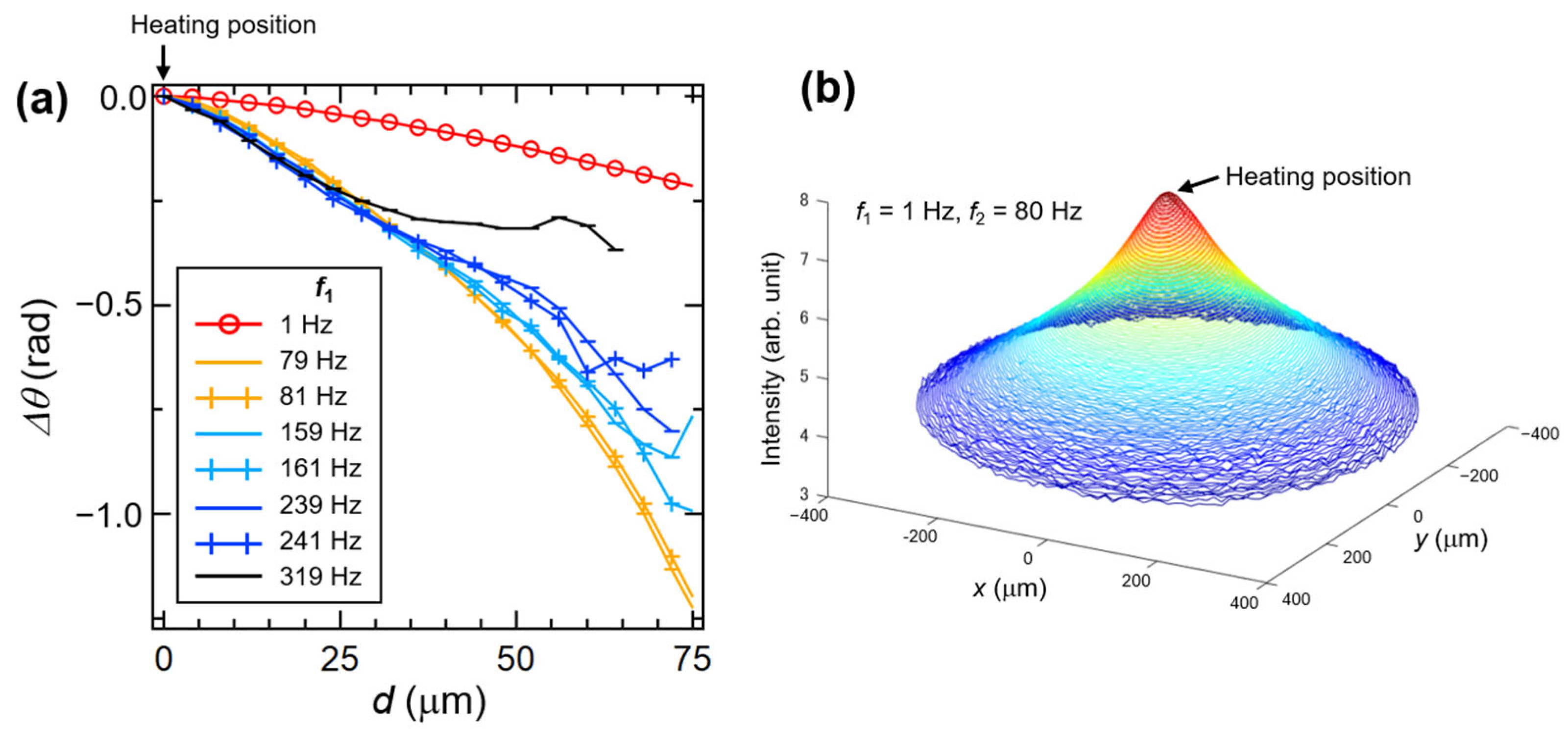
The method was applied in our analysis of the polymer film sample. The results are shown in Figure 2. The phase image at different heating frequencies f₁ were estimated by Fourier-transforming the raw image of the temperature response taken at a frame rate of f₂ = 80 Hz. The frequency of the heating was set to ±1 Hz of nf₂ (n:integer), so that FT analysis was always performed at Δf = 1 Hz. The phase was linearly delayed as a function of the distance from the heating position. The thermal diffusivity of the sample was mainly estimated from the slope of the distance dependency of the phase.

As the heating frequency f₁ increases_, the decay rate of temperature modulation becomes very high, and the amplitude modulation component of the temperature response rapidly decays below the thermal noise level. As a result, phase analysis becomes scattered when moving a certain distance away from the heating position. The position-dependent linear profile was analyzed by averaging the two-dimensional phase distribution along the azimuthal direction (Figure 3a).

The sample demonstrated in the presented results is isotropic; thus, the average value around the heating position represents the averaged in-plane thermophysical properties of the thin film sample. Figure 3b shows the 3D representation of the amplitude of periodic temperature response. The Z axis is the amplitude of the 1 Hz component, and the x–y axis corresponds to the spatial position around the heating spot. A conical surface was obtained for all frequencies, showing that the sample has isotropic thermal diffusivity.

5. Conclusions

The in-plane thermal diffusivity of polymer film was investigated using the focused laser-coupled thermal imaging technique. The thermal diffusivity of the sample was estimated from the distribution of the phase delay from the heating point by near-infrared laser. The method enables non-contact estimation of the thermophysical properties using a wide range of heating frequencies, which can be potentially applied to wide variety of materials.