Abstract
Whereas classical physics generally predicts an exponential trend for the temporal decay of an unstable state, quantum mechanics provides a rather different description. The decay is initially quadratic, while at very large times it follows a power-law. Actually, the latter regime has never been observed experimentally. Here we employ arrays of femtosecond-laser-written optical waveguides to optically realize quantum systems where a discrete state is coupled to and can decay into a continuum. The transverse optical modes represent distinct quantum states of the photon and the temporal evolution of the system is mapped into the longitudinal propagation coordinate. By injecting laser light in the fabricated structures, and by imaging with high dynamic range the scattered light from above, we are able to observe experimentally different decay regimes, including the power-law tail. This process can be viewed as the quantum simulation of a quantum decay phenomenon.
1. Introduction
According to classical physics, the population of an unstable state, coupled to a continuum, decays exponentially with time. A quantum mechanical description, however, predicts quite a different behaviour (see Figure 1a) [1]. The survival probability is initially quadratic: for —the so-called quantum-Zeno regime—where the Zeno time is proportional to the coupling strength. The decay becomes approximately exponential only at intermediate times. Such exponential regime, depending on the system parameters, may persist for quite a long time, but not indefinitely. Indeed, at very large times, a power-law regime is present with superimposed oscillations (with depending on the specific Hamiltonian of the system), under the physically motivated assumption that the spectrum of the Hamiltonian is bounded from below.
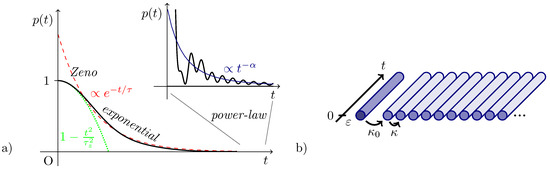
Figure 1.
(a) Typical temporal evolution of the survival probability of a discrete quantum state coupled to a continuum, where different regimes can be observed at short, intermediate and late evolution times. (b) The system is a linear array of optical waveguides, coupled by evanescent-field interaction, excited with coherent light. The first waveguide represents the discrete state and is coupled to the remaining part of the array, which acts as a continuum of states. The temporal evolution of the system is mapped into the longitudinal propagation coordinate t. See the text for details.
The “Zeno” region has been experimentally confirmed on different physical systems [2,3]. On the other hand, power-law tails have escaped so far the experimental observation. In fact, this peculiar regime usually sets in when the preceding exponential decay has strongly depleted the initial state, at a point that makes any subsequent observation prohibitively difficult.
Integrated photonics has provided in the recent years a powerful platform to optically visualize several quantum phenomena [4,5] including Bloch oscillations [6,7], Anderson localization [8] and even the quadratic decay regime [3]. In fact, the optical modes of an engineered array of waveguides may represent distinct quantum states of the photon, which can tunnel from one mode to the other by evanescent-field interaction. The temporal evolution of the system is mapped into the longitudinal propagation coordinate. By exploiting e.g., waveguide fluorescence [6], or scanning-tunneling-optical-microscopy techniques [3], it is possible to measure the light distribution in the array along the propagation, and thus investigate with high resolution the system evolution.
Here we employ arrays of single-mode optical waveguides, fabricated by femtosecond laser direct writing [9], to implement quantum systems where a discrete state is coupled and can decay into a continuum. We fabricate several structures, tuning the system parameters in order to clearly discern different decay regimes. To probe the system we couple coherent light into the array and, by acquiring an image from above of the scattered light, we are able to measure the population of the different states with a high dynamic range. We can observe not only quadratic and exponential decay trends, but also the power-law decay at long evolution times.
2. Results
We investigate linear arrays of 40 single-mode optical waveguides, fabricated in ∼10-cm long fused silica samples, where neighbouring optical modes are coupled by evanescent-field interaction (see Figure 1b). The first waveguide represents the discrete state and is coupled to the second one by a coefficient , while the other ones are coupled by a coefficient , generating a band of states of width . The first waveguide also yields a propagation constant detuning that corresponds to the energy detuning of the site, while all other waveguides are identical. In our photonic structures, the coupling coefficients depend on the relative distance between the waveguides, while the propagation constant detuning can be governed by varying the writing speed [10].
To excite the initial state of the system, with only the discrete state being populated, we inject coherent light from a He:Ne laser, horizontally polarized, into the first waveguide of the array. To acquire a picture from above of the light scattered from the waveguides, we employ a microscope-assembly composed of a 10× objective and an 8-bit monochrome CCD camera, mounted vertically on translation stages. The longitudinal motion is motorized and computer-controlled: we synchronize the CCD image acquisition with the stage motion using a MATLAB script, in order to operate the apparatus similarly to an image scanner. To enhance the dynamic range of the image acquisition, we combine pictures taken at different exposure times. Figure 2 shows a photograph of our experimental setup while a measurement is being taken, and an example of image acquired with this technique. The main quantity to probe the system evolution is the survival probability of the initial state . This is measured, as a function of the propagation coordinate t, as the ratio of the optical power scattered from the first waveguide over the global scattered power at each t.

Figure 2.
Coherent light from a He:Ne laser is injected in the array. To characterize the light distribution in the photonic structure, scattered light is imaged from above using a movable microscope-assembly that scans automatically the full length of the glass chip (a). Panel (b) reports an example of acquired intensity distribution from a waveguide array. The original image is monochrome and corresponds to a physical region of about 88 mm × 640 m; here it is reshaped for better readability and shown in false colors. A horizontal section yields the time evolution of a given state (waveguide). A vertical section gives the probability distribution within the photonic modes at a given time. Laser light is coupled in the array from the left in the topmost waveguide; the intensity of the first line in the picture thus corresponds to the survival probability of the initial state.
The initial Zeno region and the subsequent exponential decay are manifest in the evolution of a system in which the discrete state is weakly coupled to the continuum. Figure 3a reports the measured survival probability for a system with , where a detuning is applied to the first waveguide. After the initial Zeno region, the decay closely follows an exponential curve. The power-law decay tail here would set in at longer times, not investigated in the experiment.
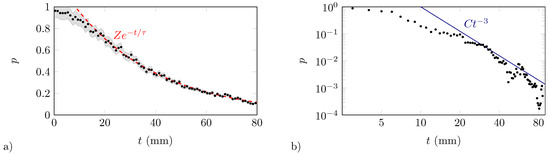
Figure 3.
(a) Experimental survival probability in a weakly coupled system (). The measured points (black dots) are encircled by a gray area indicating the experimental uncertainty. (b) Experimental survival probability in a system with stronger coupling (); the red dashed line is a fitted asymptotic trend.
The power-law tail is better evidenced in systems with stronger coupling. Figure 3b shows the measured decay in a system with and . The system parameters have been tuned to make the polynomial decay evident at times compatible with our experimental constraints (namely, the length of the glass samples). Small superimposed oscillations are also observed.
3. Discussion
We have reported the observation of different decay regimes of a quantum system, including the power-law tail at long evolution times, using an integrated-photonic experimental platform. Our characterization technique, which relies on the scattered light, differs from the one used in many other experiments on quantum-optical analogies reported in the literature [4,5], which was instead based on fluorescence. The use of scattering emission, combined with a multi-exposure imaging technique, indeed allowed for an excellent measurement linearity in an unprecedented dynamic range.
These results may disclose new perspectives in the study of quantum decay dynamics [11], as well as in the experimental investigation of complex interactions between a system and its environment, including non-Markovianity.
4. Materials and Methods
Waveguide Fabrication
Waveguides were fabricated in fused-silica substrates by femtosecond laser direct writing [9]. This technique exploits the nonlinear absorption of focused ultrashort laser pulses to induce a permanent and localized refractive index increase in the bulk of transparent dielectric materials. Waveguides are inscribed by translating the substrate with respect to the laser focus along the desired path. In detail, here we used the second harmonic (520 nm wavelength) of a commercial ytterbium-based femtosecond laser system (HighQ Spirit One), producing 400-fs-duration laser pulses at 20 kHz repetition rate. To obtain single-mode waveguides (at the wavelength of 633 nm) laser pulses with an energy of 350 nJ are focused, by means of a 0.45 NA microscope objective, 170 m below the glass surface, while the substrate is translated at constant speed, comprised between 20 and 34 mm/s.
Author Contributions
S.P., R.O., F.S. and P.M. conceived the experiment; A.C. and R.O. designed, fabricated and characterized the photonic devices; F.V.P., P.F., H.N. and S.P. performed analytical and numerical calculations in order to support the design of the photonic devices and the data analysis; A.C. wrote the paper, which was revised by all authors.
Acknowledgments
R.O. acknowledges the European Research Council (ERC) Advanced Grant—CAPABLE project (grant agreement 742745). P.F. and S.P. are partially supported by Istituto Nazionale di Fisica Nucleare (INFN) through the project “QUANTUM”. F.V.P. is supported by INFN through the project “PICS”. P.F. is partially supported by the Italian National Group of Mathematical Physics (GNFM-INdAM).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nakazato, H.; Namiki, M.; Pascazio, S. Temporal behavior of quantum mechanical systems. Int. J. Mod. Phys. B 1996, 10, 247. [Google Scholar] [CrossRef]
- Wilkinson, S.R.; Bharucha, C.F.; Fischer, M.C.; Madison, K.W.; Morrow, P.R.; Niu, Q.; Sundaram, B.; Raizen, M.G. Experimental evidence for non-exponential decay in quantum tunnelling. Nature 1997, 387, 575–577. [Google Scholar] [CrossRef]
- Biagioni, P.; Della Valle, G.; Ornigotti, M.; Finazzi, M.; Duo, L.; Laporta, P.; Longhi, S. Experimental demonstration of the optical Zeno effect by scanning tunneling optical microscopy. Opt. Express 2008, 16, 3762–3767. [Google Scholar] [CrossRef] [PubMed]
- Longhi, S. Quantum-optical analogies using photonic structures. Laser Photonics Rev. 2009, 3, 243–261. [Google Scholar] [CrossRef]
- Szameit, A.; Nolte, S. Discrete optics in femtosecond-laser-written photonic structures. J. Phys. B 2010, 43, 163001. [Google Scholar] [CrossRef]
- Chiodo, N.; Della Valle, G.; Osellame, R.; Longhi, S.; Cerullo, G.; Ramponi, R.; Laporta, P.; Morgner, U. Imaging of Bloch oscillations in erbium-doped curved waveguide arrays. Opt. Lett. 2006, 31, 1651–1653. [Google Scholar] [CrossRef] [PubMed]
- Corrielli, G.; Crespi, A.; Della Valle, G.; Longhi, S.; Osellame, R. Fractional Bloch oscillations in photonic lattices. Nat. Commun. 2014, 4, 1555. [Google Scholar] [CrossRef] [PubMed]
- Martin, L.; Di Giuseppe, G.; Perez-Leija, A.; Keil, R.; Dreisow, F.; Heinrich, M.; Nolte, S.; Szameit, A.; Abouraddy, A.F.; Christodoulides, D.N.; Saleh, B.E. Anderson localization in optical waveguide arrays with off-diagonal coupling disorder. Opt. Express 2011, 19, 13636–13646. [Google Scholar] [CrossRef]
- Osellame, R.; Cerullo, G.; Ramponi, R. (Eds.) Femtosecond Laser Micromachining: Photonic and Microfluidic Devices in Transparent Materials; Springer: Berlin/Heidelberg, Germany, 2012; ISBN 978-3-642-23365-4. [Google Scholar]
- Crespi, A.; Longhi, S.; Osellame, R. Photonic realization of the quantum Rabi model. Phys. Rev. Lett. 2012, 108, 163601. [Google Scholar] [CrossRef]
- Crespi, A.; Pepe, F.V.; Facchi, P.; Sciarrino, F.; Mataloni, P.; Nakazato, H.; Pascazio, S.; Osellame, R. Experimental investigation of quantum decay at short, intermediate and long times via integrated photonics. Phys. Rev. Lett. 2019, 122, 130401. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).