Degradation and Protection of Entanglement in Open Quantum Systems †
Abstract
:1. Introduction
2. Materials and Methods
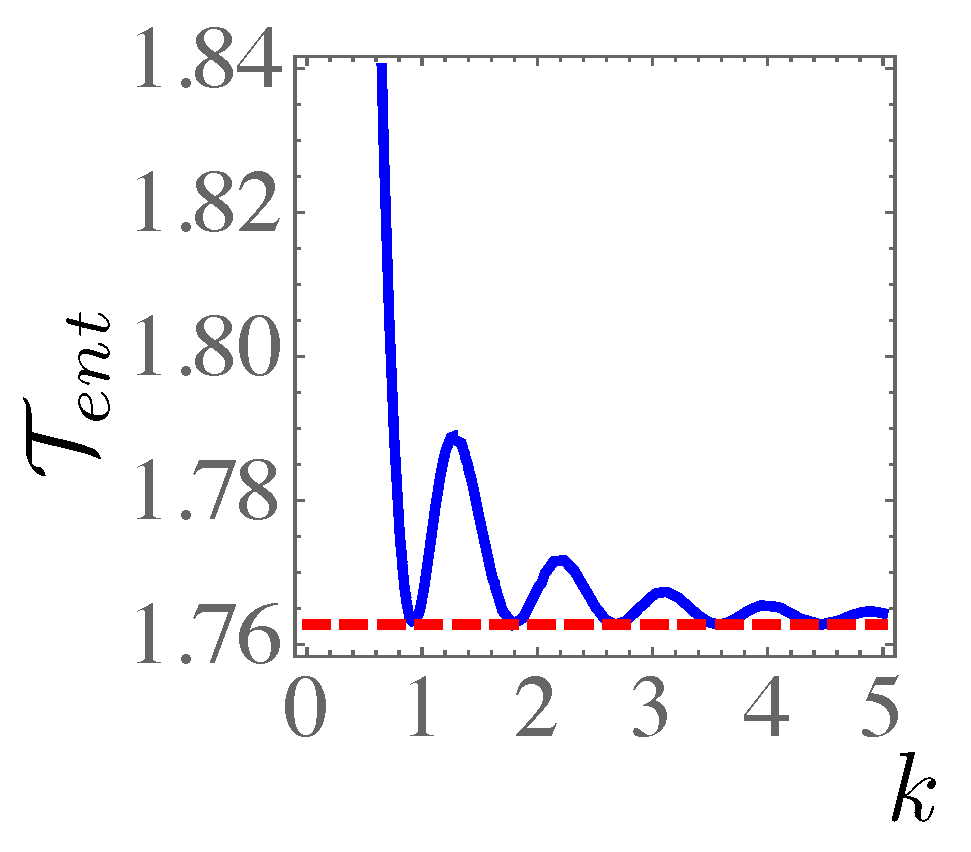
3. Results
Acknowledgments
Conflicts of Interest
References
- Holevo, A.S. Quantum Systems, Channels, Information: A Mathematical Introduction; De Gruyter: Berlin, Germany, 2012. [Google Scholar]
- De Pasquale, A.; Giovannetti, V. Quantifying the noise of a quantum channel by noise addition. Phys. Rev. A 2012, 86, 052302. [Google Scholar] [CrossRef]
- Holevo, A.S. Quantum coding theorems. Russ. Math. Surv. 1999, 53, 1295–1331. [Google Scholar] [CrossRef]
- Bellomo, B.; De Pasquale, A.; Gualdi, G.; Marzolino, U. A tomographic approach to non-Markovian master equations. J. Phys. A Math. Theor. 2010, 43, 395303. [Google Scholar] [CrossRef]
- Gatto, D.; De Pasquale, A.; Giovannetti, V. Degradation of entanglement in Markovian noise. Phys. Rev A 2019, 99, 032307. [Google Scholar] [CrossRef]
- Gorini, V.; Kossakowski, A.; Sudarshan, E. C. G. J. Math. Phys. 1976, 17, 821. [CrossRef]
- Lindblad, G. Commun. Math. Phys. 1976, 48, 119. [CrossRef]
- Rivas, A.; Huelga, S.F.; Plenio, M.B. Entanglement and non-Markovianity of quantum evolutions. Phys. Rev. Lett. 2010, 105, 050403. [Google Scholar] [CrossRef] [PubMed]
- Cuevas, Á.; De Pasquale, A.; Mari, A.; Orieux, A.; Duranti, S.; Massaro, M.; Di Carli, A.; Roccia, E.; Ferraz, J.; Sciarrino, F.; et al. Cut-and-paste restoration of entanglement transmission. Phys. Rev. A 2017, 96, 012314. [Google Scholar] [CrossRef]
- Cuevas, Á.; De Pasquale, A.; Mari, A.; Orieux, A.; Duranti, S.; Massaro, M.; Di Carli, A.; Roccia, E.; Ferraz, J.; Sciarrino, F.; et al. Amending entanglement-breaking channels via intermediate unitary operations. Phys. Rev. A 2017, 96, 022322. [Google Scholar] [CrossRef]
- De Pasquale, A.; Mari, A.; Porzio, A.; Giovannetti, V. Amendable Gaussian channels: Restoring entanglement via a unitary filter. Phys. Rev. A 2013, 87, 062307. [Google Scholar] [CrossRef]
- Rigovacca, L.; Farace, A.; De Pasquale, A.; Giovannetti, V. Gaussian Discriminating Strength. Phys. Rev. A 2015, 92, 042331. [Google Scholar] [CrossRef]
- Bullock, T.; Cosco, F.; Haddara, M.; Raja, S.H.; Kerppo, O.; Leppäjärvi, L.; Siltanen, O.; Talarico, N.W.; De Pasquale, A.; Giovannetti, V.; et al. Entanglement Protection via Periodic Environment Resetting in Continuous Time Quantum Dynamical Processes. Phys. Rev. A 2018, 98, 042301. [Google Scholar] [CrossRef]
- Facchi, P.; Pascazio, S. Progress in Optics; Wolf, E., Ed.; Elsevier: Amsterdam, The Netherlands, 2001; Volume 42, Chapter 3; pp. 147–218. [Google Scholar]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pasquale, A.D. Degradation and Protection of Entanglement in Open Quantum Systems †. Proceedings 2019, 12, 40. https://doi.org/10.3390/proceedings2019012040
Pasquale AD. Degradation and Protection of Entanglement in Open Quantum Systems †. Proceedings. 2019; 12(1):40. https://doi.org/10.3390/proceedings2019012040
Chicago/Turabian StylePasquale, Antonella De. 2019. "Degradation and Protection of Entanglement in Open Quantum Systems †" Proceedings 12, no. 1: 40. https://doi.org/10.3390/proceedings2019012040
APA StylePasquale, A. D. (2019). Degradation and Protection of Entanglement in Open Quantum Systems †. Proceedings, 12(1), 40. https://doi.org/10.3390/proceedings2019012040



