Abstract
The ultrastrong coupling regime of light-matter interaction is achieved when the coupling strength is a significant fraction of the natural frequencies of the noninteracting parts. Physics in this regime has recently attracted great interest, both theoretically and experimentally being a fruitful platform to test fundamental quantum mechanics in a new non-perturbative regime, and for applications to quantum technologies.Here we discuss the generation of photon-pair states, which is a distinctive feature of this new regime, and interesting new dynamicsl effects both in optomechanics and in circuit-QED architectures.
1. Introduction
Light-matter interaction is a fundamental building block of Nature leading to countless applications, including the forefront demonstration of supremacy of quantum technologies [1,2]. Circuit-QED solid-state systems are one of the forefront platforms for quantum hardware [3] implementing paradigmatic models where fundamental physics from measurement theory [4] to quantum thermodynamics [5] and quantum communication [6] can be studied. In the last few years a new ultrastrong coupling (USC) regime, where light-matter coupling is large enough to break the rotating wave approximation (RWA), has been achieved in cavity and circuit QED, THz metamaterials, intersubband polaritons and other physical systems [7,8], and has been subject of extensive theoretical analysis [7,8,9,10,11,12,13,14] showing thatnovel and outstanding physics arises in this non-perturbative regime. In very recent work it has been shown that USC can be a powerful tool for the generation of photon pairs from entangled states in optomechanical systems [15] and circuit-QED architectures [16]. New results on the dynamics of photons are here reported.
2. Casimir Radiation from Optomechanical Systems
Dynamical Casimir effect (DCE) consists in generation of photons from the quantum vacuum due to rapid changes of the boundary conditions. Creation of photons triggered by moving mirrors, was first predicted in 1970 [17], and later it was shown that photons can be generated also by a single mirror [18]. Tho different strategies have been considered for the experimental demonstration of DCE, namely: (1) in a device with a movable mirror able to oscillate very fast [19], or (2) inducing modulated boundary conditions mimicking an effective motion [20,21]. According to the theoretical description [22] the experimental detection of the DCE is still challenging due to the fabrication of very fast movable mirrors. Indeed for the DCE to be observed the mechanical oscillation frequency has to be at least twice the frequency of the lowest cavity mode, . Nowadays, such a condition still represents the biggest issue for the demontration of the mechanical DCE. This is why a lot of interest was driven to the implementation of the analog of DCE by time dependent boundary conditions. In the last decade [21] this strategy was implemented by superconducting circuits coupled to a coplanar transmission line terminated with a SQUID, whose inductance modulated at high frequency results in a time dependent reflectivity. Recently, a very interesting way to overcome the experimental observation of a true mechanical DCE was proposed by Macrí et al. [15]. In this work a careful theoretical description of the optomechanical interaction was studied, showing that the required matching condition can be softened. Indeed the full Hamiltonian, for a single light mode interacting with a mechanical moveable mirror is:
where and , represent respectively the annihilation (creation) operators of cavity mode and mechanical oscillator, G being the coupling strength. Notice that by writing in normal order the interaction term we can identify the standard optomechanical coupling term describing the energy induced by the radiation pressure, , and the additional term . This latter is routinely neglected owing to its perturbative action, since the mechanical frequency is usually considered much smaller than the optical frequency (as it happens in the standard experimental conditions) and because of the weak coupling regime, i.e., G is small compared to the bare energies. However this is not true in the non-perturbative USC regime where cannot be neglected anymore.
Eigenvalues of as a function of for fixed G and are reported in Figure 1b, showing the appearance of a peculiar avoided level crossing between states with 2 photons and 4 phonos, and between 2 photons and 3 phonons (magnified in Figure 1c,d). In general is able to induce resonant optomechanical scattering processes involving , where n (k) labels the photon (phonon) state, the subscript indicates which mechanical manifold is considered, and q is an integer number. Such avoided crossings occur when the energies of the final and initial states coincide, i.e., , marking the coherent exchange of excitations between light and mechanical oscillator. This result shows that the main difficulty for the detection of mechanical DCE, namely very large mechanical frequency are not necessary, is overcome since can be also smaller than even for . Of course for larger q the induced level splitting decreases, and the dynamical detection may become fragile with respect to the decoherence and losses, but for , the splitting is still larger than the losses rate achievable with the best state-of-art optomechanical systems. The reversible dynamics subsumed by , can be tested either by preparing the system in one of the mechanical Fock state and let it evolve, or by an external coherent drive (pulsed or continuous) exciting the oscillator and detecting the photon-conversion of the excitation. In both cases measurement of the generated Casimir photons requires that the optomechanical system is viewed as an open quantum system, whose dynamics is described by a Master Equation accounting for the generalized photodetection scheme appropriate for USC [15].
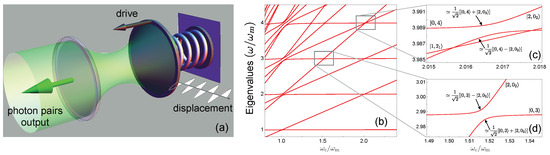
Figure 1.
(a) Schematic picture of optomechanical system: the mechanical motion of the mirror induces the generation of Casimir photons that are detectable outside the optical cavity. (b) The lowest energy levels of as a function of for fixed . (c,d) show the avoided level crossings due to the hybridization of zero- and two-photon states with mechanical states.
In Figure 2 the dynamics of an interacting optomechanical systems prepared in the two-photons Fock state of the mechanical oscillator , exchanging coherently excitations with the electromagnetic mode . Figure 2b shows the strong coupling regime, when the assocated level splitting is much larger than the losses, where an almost complete energy conversion occurs. In Figure 2a larger losses are considered, showing that a non-negligible photon rate is still measurable out of the cavity.
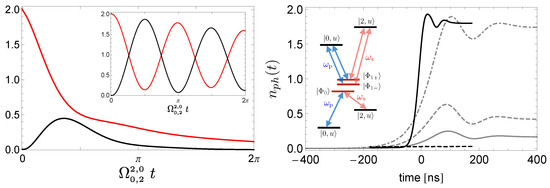
Figure 2.
Left panel. Evolution of phonons (red curves) and photons (black curves) for an optomechanical system prepared in the mechanical Fock state , for matching energy splitting, , in the weak-coupling regime with an oscillator loss rate , and a cavity loss rate . Here the energy splitting of levels and calculated for . The inset shows the same dynamics for , while the coherent exchange of excitations is almost complete. Right panel. Average photon number of STIRAP protocol for Vee (black curves) and (gray curves) scheme. Thick curve represents for the Rabi Hamiltonian including the stray couplings, while dashed lines refer to the case where only the stray RWA coupling is present. The dot dashed gray line refers to the scheme in the absence of stray couplings. The level schemes for STIRAP are shown in the inset: the Stokes (frequency , red arrows) and the pump (, blue arrows) fields couple factorized eigenstates of with selected dressed eigentates. In the scheme they are coupled to the dressed ground state (lower energy levels) while ìn the Vee scheme with the excited states (larger energy levels).
During the last year, such a new theoretical proposal for mechanical DCE has driven particular attention. In particular, in Ref. [23] the authors showed how to exploit a generalized version of DCE, in an interacting tripartite system consisting of two mechanical mirrors coupled to the same optical mode, where an excitation of a mirror can be transferred to the other involving virtual photon processes.
3. Generation of Two-Photon Pairs by STIRAP
Stimulated Raman Adiabatic Passage (STIRAP) is a coherent protocol that in its simplest version, transfers population between two quantum states along a dark state of a three-level atom, enforced by shining two light pulses in a counterintuitive sequence [26]. STIRAP is known to implement faithful complete and robust population transfer. STIRAP in superconducting nanocrcuits has been studied theoretically [27,28,29] and experimentally [30,31] since it can be used for new type of quantum gates [32] possibly resilient to solid state quantum noise [33,34,35,36,37,38]. In the USC scenario STIRAP can be used to detect virtual photons in the dressed eigenstates of the system, by coherently amplifying their conversion to real photons [16,24,25]. We consider a three-level atom (basis ) ultrastrongly coupled to a single light mode of frequency , resonant with the transition energy , described by the Hamiltonian
where is the splitting between levels respectively, and g is the coupling between the mode and the transition. Eigenstates of are partitioned in two sets: (1) factorized states , where is a Fock state, with energy ; (2) eigenstates of the two-level Rabi model with eigenvalue . Due to USC these latter are strongly entangled atom-mode states, dressed by by virtual photon pairs. A unique signature of USC in is the fact that the presence of virtual photon pairs allow in principle to transfer population from to [12]. Coherent amplification of this channel is obtained by using STIRAP. We first consider the configuration, where (see the inset of the right panel of Figure 2). The atom is prepared in and driven by an electric field yieldind , where is the ratio between atomic dipole matrix elements and is a two-tone signal. STIRAP is obtained by taking , and the envelopes where is the Stokes/pump field amplitude, is the delay, T is width of the pulses [16,25]. It may yield coherent population transfer iff , i.e., the Rabi ground state contains pairs of virtual photons. The evolution of the average number of photons in this case is shown in Figure 2 (right panel, dot-dashed gray curve). Calculations are carried out for , and . Field amplitudes and are chosen such that they yield the same Rabi frequencies for the relevant transitions, large enough to guarantee adiabaticity, , with delay . Absolute times reported in the figure correspond to .
Implementation of the protocol in artificial atoms faces the major problem that all the atomic transitions are coupled to the mode. We focus on superconducting artificial atoms where the stray coupling is accounted for by the extra term [16]. The effect is significant since a second channel for population transfer opens. The two channels interfere destructively, lowering the efficiency, as shown in Figure 2 (right panel, thick gray curve) for . Since the stray coupling alone in the RWA may yield the desired population transfer (Figure 2, right panel, dashed gray curve) measuring two photons in the cavity is anymore a smoking gun for USC, unless the stray channel is weak enough not to guarantee adiabaticity in STIRAP. This requires large anharmonicities, , and small stray coupling, , conditions which are not met in available devices.
This problem is circumvented by using the Vee field configuration, where (see the inset of the right panel of Figure 2), with intermediate states (the first excited doublet of the Rabi model). The atom is driven by a two-tone signal with and . Again STIRAP occurs only if is large enough, being nonzero only if the intermediate states contain virtual photons. Figure 2 (right panel, thick black curve) shows how the two-photon state populates under Vee STIRAP. Differently than before, the Vee configuration allows to cancel the effect of the stray coupling with available hardware, for instance flux qubits, as shown in Figure 2 (right panel, dashed black curve). Therefore Vee STIRAP guarantees that we finally observe in the cavity two virtual photons converted in real, i.e., a smoking gun of USC.
Curves for Vee STIRAP in Figure 2 are obtained for , and showing that suppression of the stray channel occurs for much softer spectral constraints than for STIRAP. This remarkable property is due to the fact that the stray pattern for population transfer does not contribute to since transfer via RWA couplings only may in principle occur via a different intermediate state which is largely detuned and so weak to spoil adiabaticity and yield practically zero final population of the target state. This has the important practical consequence that the protocol requires external fields with frequencies not larger than . Moreover since the two-photon components of the dressed intermediate states are larger, the protocol in the Vee scheme is much faster. Indeed black curves in the right panel of Figure 2 are obtained for . Therefore the Vee protocol is less sensitive to decoherence and/or it may be operated with smaller field amplitudes.
4. Conclusions
In conclusion we have shown that Vee STIRAP yields the unambiguous signature of USC in available architectures of superconducting artificial atoms, via detection of two-photons by coherently amplified population transfer. On the contrary the usual scheme for STIRAP is sensitive to the presence of stray coupling, which may allow population transfer also in RWA, unless stringent spectral contraints are met, which is not true for superconducting devices. Observing also that population transfer requires less stringent conditions on the spectrum and on the external fields, we conclude that demonstration of dynamical detection of USC by Vee STIRAP is well feasible in available superconducting hardware.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Haroche, S.; Raimond, J.M. Exploring the Quantum; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Mohseni, M.; Read, P.; Neven, H.; Boixo, S.; Denchev, V.; Babbush, R.; Fowler, A.; Smelyanskiy, V.; Martinis, J. Commercialize quantum technologies in five years. Nature 2017, 543, 171. [Google Scholar] [CrossRef] [PubMed]
- Schoelkopf, R.J.; Girvin, S.M. Wiring up quantum systems. Nature 2008, 451, 664. [Google Scholar] [CrossRef] [PubMed]
- Wallraff, A.; Schuster, D.I.; Blais, A.; Frunzio, L.; Huang, R.S.; Majer, J.; Kumar, S.; Girvin, S.; Schoelkopf, R. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 2004, 421, 162–167. [Google Scholar] [CrossRef] [PubMed]
- Di Stefano, P.G.; Alonso, J.J.; Lutz, E.; Falci, G.; Paternostro, M. Nonequilibrium thermodynamics of continuously measured quantum systems: A circuit QED implementation. Phys. Rev. B 2018, 98, 144514. [Google Scholar] [CrossRef]
- Benenti, G.; D’Arrigo, A.; Falci, G. Enhancement of Transmission Rates in Quantum Memory Channels with Damping. Phys. Rev. Lett. 2009, 103, 020502. [Google Scholar] [CrossRef]
- Kockum, A.F.; Miranowicz, A.; De Liberato, S.; Savasta, S.; Nori, F. Ultrastrong coupling between light and matter. Nat. Rev. Phys. 2019, 1, 19–40. [Google Scholar] [CrossRef]
- Forn-Diaz, P.; Lamata, L.; Rico, E.; Kono, J.; Solano, E. Ultrastrong coupling regime of light-matter interaction. arXiv 2018, arXiv:1804.09275. [Google Scholar] [CrossRef]
- Niemczyk, T.; Deppe, F.; Huebl, H.; Menzel, E.P.; Hocke, F.; Schwarz, M.J.; Garcia-Ripoll, J.J.; Zueco, D.; Hümmer, T.; Solano, E.; et al. Circuit quantum electrodynamics in the ultrastrong-coupling regime. Nat. Phys. 2010, 6, 772. [Google Scholar] [CrossRef]
- Ridolfo, A.; Leib, M.; Savasta, S.; Hartmann, M.J. Photon Blockade in the Ultrastrong Coupling Regime. Phys. Rev. Lett. 2012, 109, 193602. [Google Scholar] [CrossRef]
- Ridolfo, A.; Savasta, S.; Hartmann, M.J. Nonclassical Radiation from Thermal Cavities in the Ultrastrong Coupling Regime. Phys. Rev. Lett. 2013, 110, 163601. [Google Scholar] [CrossRef]
- Stassi, R.; Ridolfo, A.; Di Stefano, O.; Hartmann, M.J.; Savasta, S. Spontaneous Conversion from Virtual to Real Photons in the Ultrastrong-Coupling Regime. Phys. Rev. Lett. 2013, 110, 243601. [Google Scholar] [CrossRef] [PubMed]
- Garziano, L.; Ridolfo, A.; Stassi, R.; Di Stefano, O.; Savasta, S. Switching on and off of ultrastrong light-matter interaction: Photon statistics of quantum vacuum radiation. Phys. Rev. A 2013, 88, 063829. [Google Scholar] [CrossRef]
- Di Stefano, O.; Kockum, A.F.; Ridolfo, A.; Savasta, S.; Nori, F. Photodetection probability in quantum systems with arbitrarily strong light-matter interaction. Sci. Rep. 2018, 8, 17825. [Google Scholar] [CrossRef]
- Macrì, V.; Ridolfo, A.; Di Stefano, O.; Kockum, A.F.; Nori, F.; Savasta, S. Nonperturbative Dynamical Casimir Effect in Optomechanical Systems: Vacuum Casimir-Rabi Splittings. Phys. Rev. X 2018, 8, 011031. [Google Scholar] [CrossRef]
- Falci, G.; Ridolfo, A.; Di Stefano, P.G.; Paladino, E. Ultrastrong coupling probed by Coherent Population Transfer. arXiv 2017, arXiv:1708.00906. [Google Scholar] [CrossRef] [PubMed]
- Moore, G.T. Quantum Theory of the Electromagnetic Field in a Variable-Length One-Dimensional Cavity. J. Math. Phys. (N. Y.) 1970, 11, 2679. [Google Scholar] [CrossRef]
- Fulling, S.A.; Davies, P.C.W. Radiation from a moving mirror in two dimensional space-time: conformal anomaly. Proc. R. Soc. A 1976, 348, 393. [Google Scholar]
- Sassaroli, E.; Srivastava, Y.N.; Widom, A. Photon production by the dynamical Casimir effect. Phys. Rev. A 1994, 50, 1027. [Google Scholar] [CrossRef]
- Johansson, J.R.; Johansson, G.; Wilson, C.M.; Nori, F. Dynamical Casimir Effect in a Superconducting Coplanar Waveguide. Phys. Rev. Lett. 2009, 103, 147003. [Google Scholar] [CrossRef]
- Wilson, C.M.; Johansson, G.; Pourkabirian, A.; Simoen, M.; Johansson, J.R.; Duty, T.; Nori, F.; Delsing, P. Observation of the dynamical Casimir effect in a superconducting circuit. Nature 2011, 479, 376. [Google Scholar] [CrossRef]
- Lambrecht, A.; Jaekel, M.T.; Reynaud, S. Motion Induced Radiation from a Vibrating Cavity. Phys. Rev. Lett. 1996, 77, 615. [Google Scholar] [CrossRef] [PubMed]
- Di Stefano, O.; Settineri, A.; Macrì, V.; Ridolfo, A.; Stassi, R.; Kockum, A.F.; Savasta, S.; Nori, F. Interaction of Mechanical Oscillators Mediated by the Exchange of Virtual Photon Pairs. Phys. Rev. Lett. 2019, 122, 030402. [Google Scholar] [CrossRef] [PubMed]
- Falci, G.; Di Stefano, P.; Ridolfo, A.; D’Arrigo, A.; Paraoanu, G.; Paladino, E. Advances in quantum control of three-level superconducting circuit architectures. Fortschr. Phys. 2017, 65, 1600077. [Google Scholar] [CrossRef]
- Ridolfo, A.; Falci, G.; Pellegrino, F.M.D.; Maccarrone, G.D.; Paladino, E. Photon pair production by STIRAP in ultrastrongly coupled matter-radiation systems. Eur. Phys. J. Spec. Top. 2019, 227, 2183–2188. [Google Scholar] [CrossRef]
- Vitanov, N.V.; Rangelov, A.A.; Shore, B.W.; Bergmann, K. Stimulated Raman adiabatic passage in physics, chemistry, and beyond. Rev. Mod. Phys. 2017, 89, 015006. [Google Scholar] [CrossRef]
- Siewert, J.; Brandes, T.; Falci, G. Advanced control with a Cooper-pair box: Stimulated Raman adiabatic passage and Fock-state generation in a nanomechanical resonator. Phys. Rev. B 2009, 79, 024504. [Google Scholar] [CrossRef]
- Di Stefano, P.G.; Paladino, E.; Pope, T.J.; Falci, G. Coherent manipulation of noise-protected superconducting artificial atoms in the Lambda scheme. Phys. Rev. A 2016, 93, 051801. [Google Scholar] [CrossRef]
- Di Stefano, P.G.; Paladino, E.; D’Arrigo, A.; Falci, G. Population transfer in a Lambda system induced by detunings. Phys. Rev. B 2015, 91, 224506. [Google Scholar] [CrossRef]
- Kumar, K.; Vepsäläinen, A.; Danilin, S.; Paraoanu, G. Stimulated Raman adiabatic passage in a three-level superconducting circuit. Nat. Commun. 2016, 7, 10628. [Google Scholar] [CrossRef]
- Xu, H.K.; Song, C.; Liu, W.Y.; Xue, G.M.; Su, F.F.; Deng, H.; Tian, Y.; Zheng, D.N.; Han, S.; Zhong, Y.P.; et al. Coherent population transfer between uncoupled or weakly coupled states in ladder-type superconducting qutrits. Nat. Commun. 2016, 7, 11018. [Google Scholar] [CrossRef]
- Vepsäläinen, A.; Danilin, S.; Paladino, E.; Falci, G.; Paraoanu, G.S. Quantum Control in Qutrit Systems Using Hybrid Rabi-STIRAP Pulses. Photonics 2016, 3, 62. [Google Scholar] [CrossRef]
- Paladino, E.; Galperin, Y.; Falci, G.; Altshuler, B. 1/f noise: Implications for solid-state quantum information. Rev. Mod. Phys. 2014, 86, 361–418. [Google Scholar] [CrossRef]
- D’Arrigo, A.; Mastellone, A.; Paladino, E.; Falci, G. Effects of low-frequency noise cross-correlations in coupled superconducting qubits. New J. Phys. 2008, 10, 115006. [Google Scholar] [CrossRef]
- Paladino, E.; Mastellone, A.; D’Arrigo, A.; Falci, G. Optimal tuning of solid-state quantum gates: A universal two-qubit gate. Phys. Rev. B 2010, 81, 052502. [Google Scholar] [CrossRef]
- Chiarello, F.; Paladino, E.; Castellano, M. G.; Cosmelli, C.; D’Arrigo, A.; Torrioli, G.; Falci, G. Superconducting qubit manipulated by fast pulses: experimental observation of distinct decoherence regimes. New J. Phys. 2012, 14, 023031. [Google Scholar] [CrossRef]
- Falci, G.; La Cognata, A.; Berritta, M.; D’Arrigo, A.; Paladino, E.; Spagnolo, B. Design of a Lambda system for population transfer in superconducting nanocircuits. Phys. Rev. B 2013, 87, 214515-1–214515-13. [Google Scholar] [CrossRef]
- Paladino, E.; D’Arrigo, A.; Mastellone, A.; Falci, G. Decoherence times of universal two-qubit gates in the presence of broad-band noise. New J. Phys. 2011, 13. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).