Abstract
Quantum enhanced optical measurement protocols aim at reducing the uncertainty in the estimation of some physical quantities of a system below the shot-noise limit, classically unavoidable. In particular when small number of photons is used the shot noise can be the main source of uncertainty, in these cases the use of quantum light is of great interest. Note that there are several situations where the number of photons in the probe can not be increased arbitrarily, as when fragile biological samples are under investigation. Two different imaging protocols are discussed in the following.
1. Introduction
Here we present the potentialities and the achievements of the use of non-classical photon-number correlations in twin-beam states (TWB) in a couple of imaging protocols [1]. The fundamental property of this state is that it is entangled in the photon number meaning that two ideal detectors intercepting each mode respectively always measure the same number of photons (only phase-insensitive intensity measurements are necessary). Each beam presents a thermal statistic, but the fluctuations between the two beams are correlated at the quantum level. Moreover, TWB state can be easily experimentally produced by the spontaneous parametric down conversion process in a non linear crystal (e.g., Barium borate crystal, BBO). Differently respect to the entanglement, quantum correlations are robust against unavoidable experimental losses. In particular the degree of correlation between the modes can be quantified using a figure of merit named noise reduction factor (NRF), defined as . For TWB-state and perfect detection efficiency () it follows , while for classical shot-noise limited bipartite states . It can be shown, see for example [1], that TWB-state for not unitary detection efficiency , leads to , i.e., shows intensity correlations below the shot-noise limit.
Exploitation of quantum correlations could offer advantages in every protocol where the comparison between a probe and a reference beam is considered. The idea is that using one beam of the pair as a probe and the other as a reference, the strong correlation helps to detect slight modifications in the signals when the two beams are compared.
2. Absorption Measurement
On one side we focus on absorption measurements, presenting the work done in [2].
Quantum mechanics laws set the ultimate limit to the sensitivity in this kind of measurement, constrained by the probe mean energy [3]. We demonstrate that TWB allows reaching the ultimate quantum limit for all energy regimes (even less than one photon per mode) with the simplest measurement strategy. One beam of the pair addresses the sample, while the second one is used as a reference to compensate both for classical drifts and for fluctuation at the most fundamental quantum level. We propose and deeply discuss different absorption estimators, focusing on their relation with the ultimate quantum limit and on the role of experimental losses.
Finally we perform the experiment. The experimental set-up is reported in Figure 1. In the BBO crystal two beamswith perfect correlation in the photon number (TWB state) are generated.
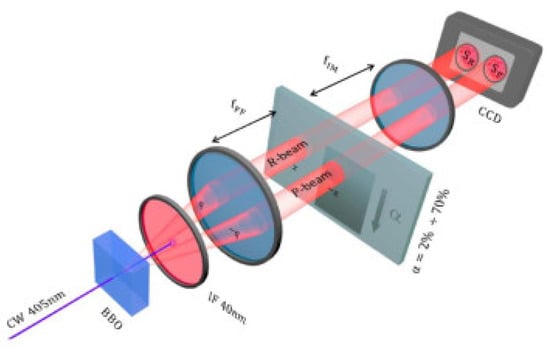
Figure 1.
Experimental set-up used to demonstrate quantum enhancement in absorption measurements.
The probe beam passes trough the sample and is then detected in the region of the CCD, on the contrary the reference beam goes directly to , without interacting with the sample. Absorption levels from 2 to 70% are considered. Different absorption estimators are discussed, in particular:
- . and are the number of photons on in two different moments, when the sample is present and when it has been removed respectively. Since the single beam is well approximated by a coherent beam (being a thermal beam with very low number of photons per mode), the uncertainty on is close to the best classical case (). Note that this strategy does not take into account possible drifts of the source, therefore two mode strategy should be preferred in real situations for having unbiased estimation.
- . and are the number of photons on and respectively and is the unbalance between the two beams, obtained from a preliminary acquisition without the sample inserted. Exploiting the correlation between the two beams it is possible to go below the classical limit, reaching the ultimate quantum limit in the ideal case of unitary efficiencies. The presence of losses leads to a detachment from the ultimate quantum limit .
- . In this case and have been chosen in order to be only classically correlated.
In Figure 2 the experimental data and the theoretical curves are reported. Plain colored curves are the theoretical curves in presence of experimental losses, independently estimated. In particular in our case we have . Green curve and data correspond to the TWB case in our experimental conditions (). Blue curve and data correspond to the classical single mode case (). Orange data refer to the classical two-mode case (). Black curves are relevant theoretical limits in case of unitary efficiency. In particular the dashed-dotted line () is the ultimate quantum limit [3], i.e., the minimum uncertainty on that can be obtained according to the limits imposed by quantum mechanics. The dashed line () is the coherent limit, i.e., the minimum uncertainty on that can be obtained when classical light is used. The dotted line () represents the case of two classically correlated beams of equal intensity. The quantum enhancement is preserved up to a sample loss of ∼70%. For a quantum enhancement of around 40% has been measured, compared to the best classical strategy. It represents, in our knowledge, the best sensitivity per photon ever reported in a loss measurement.
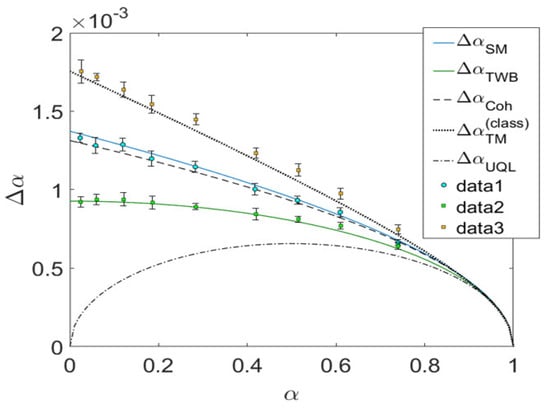
Figure 2.
Uncertainty on varying the mean absorption . A quantum enhancement of ∼40% for is demonstrated. Description of the different estimators and theoretical limits is presented in the text.
3. Optimized Ghost Imaging
On the other side we present some preliminary results about a new ghost imaging protocol, extension of the one presented in [4]. Ghost imaging is an imaging technique where the object image is retrieved by using two spatially correlated beams, proposed for the first time by Pittman [5]: the reference beam, which never interacts with the object and is measured with a multi-pixel detector, and the object beam, which, after illuminating the object is collected with a bucket detector, with no spatial resolution. By correlating the reference beam with the bucket signal, the ‘‘ghost’’ image is retrieved. The use of quantum correlated light, as TWB, leads to an important quantum enhancement, in particular when the number of photons per spatio-temporal mode is remarkably low. Different protocols are presented and some of their peculiarities discussed. The preliminary reconstruction of the transmission profile of a biological object is also presented.
Author Contributions
I.R.-B. and A.M. conceived the idea of the experiment, which were designed and discussed with input from all authors. I.R.-B. and E.L. developed the theoretical model. E.L. and A.M. realized the experimental setup and collected the data in INRIM quantum optics labs (coordinated by M.G.). All authors discussed the results.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Meda, A.; Losero, E.; Samantaray, N.; Scafirimuto, F.; Pradyumna, S.; Avella1, A.; Ruo-Berchera1, I.; Genovese, M. Photon-number correlation for quantum enhanced imaging and sensing. J. Opt. 2017, 19, 094002. [Google Scholar] [CrossRef]
- Losero, E.; Ruo-Berchera, I.; Meda, A.; Avella, A.; Genovese, M. Unbiased estimation of an optical loss at the ultimate quantum limit with twin-beams. Sci. Rep. 2018, 8, 7431. [Google Scholar] [CrossRef] [PubMed]
- Adesso, G.; Dell’Anno, F.; De Siena, S.; Illuminati, F.; Souza, L.A.M. Optimal estimation of losses at the ultimate quantum limit with non-Gaussian states. Phys. Rev. A 2009, 79, 040305. [Google Scholar] [CrossRef]
- Ferri, F.; Magatti, D.; Lugiato, L.A.; Gatti, A. Differential ghost imaging. Phys. Rev. Lett. 2010, 104, 253603. [Google Scholar] [CrossRef] [PubMed]
- Pittman, T.B.; Shih, Y.H.; Strekalov, D.V.; Sergienko, A.V. Optical imaging by means of two-photon quantum entanglement. Phys. Rev. A 1995, 52, R3429–R3432. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).