Speedup of Adiabatic Multiqubit State-Transfer by Ultrastrong Coupling of Matter and Radiation †
Abstract
:1. Introduction
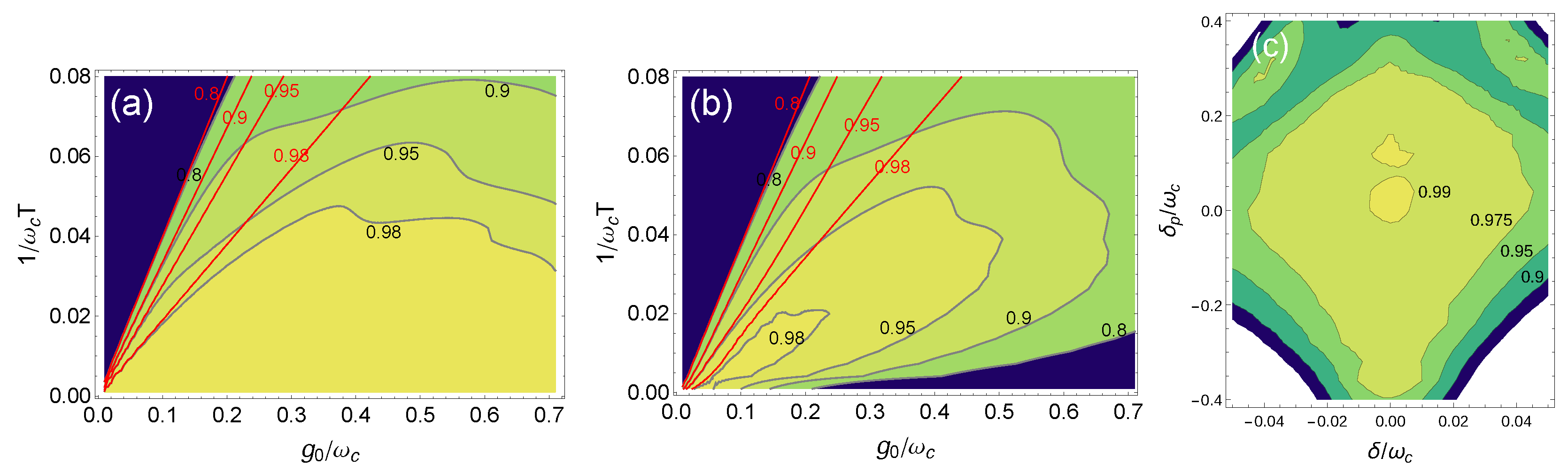
2. Multiqubit Operation in the Ultrastrong Coupling Regime
3. Conclusions
References
- Haroche, S.; Raimond, J.M. Exploring the Quantum; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Wallraff, A.; Schuster, D.I.; Blais, A.; Frunzio, L.; Huang, R.S.; Majer, J.; Kumar, S.; Girvin, S.; Schoelkopf, R. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 2004, 421, 162–167. [Google Scholar] [CrossRef] [PubMed]
- Schoelkopf, R.J.; Girvin, S.M. Wiring up quantum systems. Nature 2008, 451, 664. [Google Scholar] [CrossRef] [PubMed]
- Kelly, J. Engineering superconducting qubit arrays for quantum supremacy. In Proceedings of the American Physical Society March Meeting, Los Angeles, CA, USA, 5–9 March 2018. [Google Scholar]
- Song, C.; Xu, K.; Liu, W.; Yang, C.P.; Zheng, S.B.; Deng, H.; Xie, Q.; Huang, K.; Guo, Q.; Zhang, L.; et al. 10-Qubit Entanglement and Parallel Logic Operations with a Superconducting Circuit. Phys. Rev. Lett. 2017, 119, 180511. [Google Scholar] [CrossRef]
- Di Stefano, P.G.; Alonso, J.J.; Lutz, E.; Falci, G.; Paternostro, M. Nonequilibrium thermodynamics of continuously measured quantum systems: A circuit QED implementation. Phys. Rev. B 2018, 98, 144514. [Google Scholar] [CrossRef]
- Benenti, G.; D’Arrigo, A.; Falci, G. Enhancement of Transmission Rates in Quantum Memory Channels with Damping. Phys. Rev. Lett. 2009, 103, 020502. [Google Scholar] [CrossRef] [PubMed]
- Braak, D.; Chen, Q.H.; Batchelor, M.T.; Solano, E. Semi-classical and quantum Rabi models: in celebration of 80 years. J. Phys. A Math. Theor. 2016, 49, 300301. [Google Scholar] [CrossRef]
- Plastina, F.; Falci, G. Communicating Josephson qubits. Phys. Rev. B 2003, 67, 224514. [Google Scholar] [CrossRef]
- Gu, X.; Frisk Kockum, A.; Miranowicz, A.; Liu, Y.X.; Nori, F. Microwave photonics with superconducting quantum circuits. Phys. Rep. 2017, 718–719, 1–102. [Google Scholar]
- Benenti, G.; D’Arrigo, A. and Siccardi, S.; Strini, G. Phys. Rev. A 2014, 90, 052313. [Google Scholar] [CrossRef]
- Vitanov, N.V.; Rangelov, A.A.; Shore, B.W.; Bergmann, K. Stimulated Raman adiabatic passage in physics, chemistry, and beyond. Rev. Mod. Phys. 2017, 89, 015006. [Google Scholar] [CrossRef]
- Siewert, J.; Brandes, T.; Falci, G. Advanced control with a Cooper-pair box: Stimulated Raman adiabatic passage and Fock-state generation in a nanomechanical resonator. Phys. Rev. B 2009, 79, 024504. [Google Scholar] [CrossRef]
- Di Stefano, P.G.; Paladino, E.; Pope, T.J.; Falci, G. Coherent manipulation of noise-protected superconducting artificial atoms in the Lambda scheme. Phys. Rev. A 2016, 93, 051801. [Google Scholar] [CrossRef]
- Kumar, K.; Vepsäläinen, A.; Danilin, S.; Paraoanu, G. Stimulated Raman adiabatic passage in a three-level superconducting circuit. Nat. Comm. 2016, 7, 1062. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Song, W.Y.; Liu, G.M.; Xue, F.F.; Su, H.; Deng, Y.; Tian, D.N.; Zheng, S.; Han, Y.P.; Zhong, H.; et al. Coherent population transfer between uncoupled or weakly coupled states in ladder-type superconducting qutrits. Nat. Commun. 2016, 7, 11018. [Google Scholar] [CrossRef]
- Vepsäläinen, A.; Danilin, S.; Paladino, E.; Falci, G.; Paraoanu, G.S. Quantum Control in Qutrit Systems Using Hybrid Rabi-STIRAP Pulses. Photonics 2016, 3, 62. [Google Scholar] [CrossRef]
- Wang, Y.D.; Zhang, R.; Yan, X.B.; Chesi, S. Optimization of STIRAP-based state transfer under dissipation. New J. Phys. 2017, 19, 093016. [Google Scholar] [CrossRef]
- Falci, G.; Di Stefano, P.; Ridolfo, A.; D’Arrigo, A.; Paraoanu, G.; Paladino, E. Advances in quantum control of three-level superconducting circuit architectures. Fortschr. Phys. 2017, 65, 1600077. [Google Scholar] [CrossRef]
- Paladino, E.; Galperin, Y.; Falci, G.; Altshuler, B. 1/f noise: implications for solid-state quantum information. Rev. Mod. Phys. 2014, 86, 361–418. [Google Scholar] [CrossRef]
- Falci, G.; La Cognata, A.; Berritta, M.; D’Arrigo, A.; Paladino, E.; Spagnolo, B. Design of a Lambda system for population transfer in superconducting nanocircuits. Phys. Rev. B 2013, 87, 214515-1–214515-13. [Google Scholar] [CrossRef]
- Paladino, E.; D’Arrigo, A.; Mastellone, A.; Falci, G. Decoherence times of universal two-qubit gates in the presence of broad-band noise. New J. Phys. 2011, 13. [Google Scholar] [CrossRef]
- Felicetti, S.; Sanz, M.; Lamata, L.; Romero, G.; Johansson, G.; Delsing, P.; Solano, E. Dynamical Casimir Effect Entangles Artificial Atoms. Phys. Rev. Lett. 2014, 113, 093602. [Google Scholar] [CrossRef] [PubMed]
- Rach, N.; Müller, M.M.; Calarco, T.; Montangero, S. Dressing the chopped-random-basis optimization: A bandwidth-limited access to the trap-free landscape. Phys. Rev. A 2015, 062343, 92. [Google Scholar] [CrossRef]
- Hoeb, F.; Angaroni, F.; Zoller, J.; Calarco, T.; Strini, G.; Montangero, S.; Benenti, G. Amplification of the parametric dynamical Casimir effect via optimal control. Phys. Rev. A 2017, 033851, 96. [Google Scholar] [CrossRef]
- Di Stefano, P.G.; Paladino, E.; D’Arrigo, A.; Falci, G. Population transfer in a Lambda system induced by detunings. Phys. Rev. B 2015, 91, 224506. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stramacchia, M.; Ridolfo, A.; Benenti, G.; Paladino, E.; Pellegrino, F.M.D.; Maccarrone, D.; Falci, G. Speedup of Adiabatic Multiqubit State-Transfer by Ultrastrong Coupling of Matter and Radiation. Proceedings 2019, 12, 35. https://doi.org/10.3390/proceedings2019012035
Stramacchia M, Ridolfo A, Benenti G, Paladino E, Pellegrino FMD, Maccarrone D, Falci G. Speedup of Adiabatic Multiqubit State-Transfer by Ultrastrong Coupling of Matter and Radiation. Proceedings. 2019; 12(1):35. https://doi.org/10.3390/proceedings2019012035
Chicago/Turabian StyleStramacchia, Michele, Alessandro Ridolfo, Giuliano Benenti, Elisabetta Paladino, Francesco Maria Dimitri Pellegrino, Daniele Maccarrone, and Giuseppe Falci. 2019. "Speedup of Adiabatic Multiqubit State-Transfer by Ultrastrong Coupling of Matter and Radiation" Proceedings 12, no. 1: 35. https://doi.org/10.3390/proceedings2019012035
APA StyleStramacchia, M., Ridolfo, A., Benenti, G., Paladino, E., Pellegrino, F. M. D., Maccarrone, D., & Falci, G. (2019). Speedup of Adiabatic Multiqubit State-Transfer by Ultrastrong Coupling of Matter and Radiation. Proceedings, 12(1), 35. https://doi.org/10.3390/proceedings2019012035





