Preserving Nonclassicality in Noisy Communication Channels ^†

Abstract

Nowadays, the transmission of quantum information, especially for the distribution of cryptographic keys, is required on a global scale. The main obstacle to overcome in free-space communication is the presence of turbulence, which causes both spatial and temporal deformations of the light signals that code information. Here we investigate the extent at which the transmission of mesoscopic twin-beam states through asymmetric noisy channels degrades the nonclassical nature of the photon-number correlations between signal and idler. We consider three nonclassicality criteria, all written in terms of measurable quantities, and demonstrate, both theoretically and experimentally, that the asymmetry introduced by losses affects the three criteria in different ways.

1. Introduction

Quantum states of light represent a useful tool for coding and transmitting information. However, under realistic conditions, such as in free space communication, noise sources can affect the communication channels thus impairing the integrity of the information content [1,2].

In order to address the optimal transmission of quantum states of light, it is thus important to investigate which kinds of states and nonclassical features are more robust against losses and can survive under specific conditions.

Motivated by these requirements, we investigate the survival of nonclassical correlations between the two parties of a mesoscopic twin-beam state in the case in which one of the parties is affected by a varying loss. We consider three different nonclassicality criteria, namely the Schwarz inequality, the noise reduction factor, and a high-order inequality [3,4], and explore which one is the strictest for the observation of nonclassical correlations.

At variance with the standard investigations, which are performed with single-photon detectors, our experimental results were obtained detecting the twin-beam states by means of a pair of hybrid photodetectors endowed with partial photon-number-resolving capability [4].

2. Results

Let’s consider the multi-mode twin-beam state [4]

$$|{\psi }_{\mu }\rangle =\sum _{n=0}^{\infty }\sqrt{p_n^{\mu }}|n^{\otimes }{\rangle }_s\otimes {|n^{\otimes }\rangle }_i,$$

(1)

where $|n^{\otimes }\rangle =\delta (n-{\sum }_{h=1}^{\mu }{n}_h){\otimes }_{k=1}^{\mu }|n_k\rangle$ represents the n-photon state coming from $\mu$ equally- populated modes that impinge on the detector and

$$p_n^{\mu }=\frac{(n+\mu -1)!}{n!(\mu -1)!{(N/\mu +1)}^{\mu }{(\mu /N+1)}^n}$$

(2)

is the multimode thermal photon-number probability distribution for N mean-photon number. In order to check the pairwise correlations exhibited by the state in Equation (1), we consider three different nonclassicality criteria, all written in terms of measurable quantities, namely the noise reduction factor (NRF), the Schwarz inequality and a high-order inequality. The NRF for detected photons is defined as

$$R={\sigma }^2(m_1-m_2)/\langle m_1+m_2\rangle ,$$

(3)

where $\langle m_j\rangle$ is the mean number of photons measured in the j-th arm, whereas ${\sigma }^2$ is the variance. In order to deal with the case of a varying lossy channel [5], we assume that the detection chains have the same efficiency, and that the second channel is affected by an additional amount of loss with respect to the first channel, hereafter indicated as $\lambda =1-{\eta }_2/{\eta }_1$, being ${\eta }_2\le {\eta }_1$. By setting $\langle m_1\rangle ={\eta }_1\langle n\rangle \equiv \eta \langle n\rangle =\langle m\rangle$ and $\langle m_2\rangle ={\eta }_2\langle n\rangle =\eta (1-\lambda )\langle n\rangle$, it is possible to demonstrate [5] that for the state in Equation (1), the NRF reads as:

$$R=1-\frac{2\eta (1-\lambda )}{2-\lambda }+\frac{{\lambda }^2}{(2-\lambda )}\frac{\langle m\rangle }{\mu }.$$

(4)

It is easy to verify that the condition $R<1$, which is sufficient for nonclassicality, is satisfied for $0<\lambda <(\sqrt{1+2\langle n\rangle }-1)/\langle n\rangle$, where $\langle n\rangle =\langle m\rangle /\left(\eta \mu \right)$ is the mean number of photons per mode. The upper limit approaches unity for $\langle n\rangle \to 0$ and zero for $\langle n\rangle \to \infty$: the presence of asymmetric loss is less detrimental for sub-shot-noise correlations in the case of weak and/or multimode twin-beam states.

The second criterion we consider is the Schwarz inequality [6], $S>1$, in which

$$S=\frac{\langle m_1{m}_2\rangle }{\sqrt{\left(\langle m_1^2\rangle -\langle m_1\rangle \right)\left(\langle m_2^2\rangle -\langle m_2\rangle \right)}},$$

(5)

In the case under examination, i.e., in the presence of the asymmetric loss,

$$S=1+\frac{\mu }{\mu +1}\frac{\eta }{\langle m\rangle },$$

(6)

which always satisfies $S>1$. Nonclassicality can be also investigated by means of high-order correlation functions. Written in terms of detected photons, the generic $(j+k)$th-order correlation function is defined as $g^{jk}=\langle m_1^j{m}_2^k\rangle {\left({\langle m_1\rangle }^j{\langle m_2\rangle }^k\right)}^{-1}$. By applying the same assumption on the detection efficiencies used above, the high-order correlation functions up to the fourth order read as follows:

$$\begin{array}{ccc}\hfill g^{11}& =& G_{\mu }^1+\frac{\eta }{\langle m\rangle },\hfill \\ \hfill g^{21}& =& G_{\mu }^2+G_{\mu }^1\frac{1+2\eta }{\langle m\rangle }+\frac{\eta }{{\langle m\rangle }^2},g^{12}=G_{\mu }^2+G_{\mu }^1\frac{1+2\eta (1-\lambda )}{(1-\lambda )\langle m\rangle }+\frac{\eta }{(1-\lambda ){\langle m\rangle }^2},\hfill \\ \hfill g^{22}& =& G_{\mu }^3+G_{\mu }^2\left(\frac{1+2\eta }{\langle m\rangle }+\frac{1+2\eta (1-\lambda )}{(1-\lambda )\langle m\rangle }\right)+G_{\mu }^1\frac{1+2{\eta }^2(1-\lambda )+2\eta +2\eta (1-\lambda )}{(1-\lambda ){\langle m\rangle }^2}+\frac{\eta }{(1-\lambda ){\langle m\rangle }^3},\hfill \\ \hfill g^{31}& =& G_{\mu }^3+3G_{\mu }^2\frac{1+\eta }{\langle m\rangle }+G_{\mu }^1\frac{1+6\eta }{{\langle m\rangle }^2}+\frac{\eta }{{\langle m\rangle }^3},\hfill \\ \hfill g^{13}& =& G_{\mu }^3+3G_{\mu }^2\frac{1+\eta (1-\lambda )}{(1-\lambda )\langle m\rangle }+G_{\mu }^1\frac{1+6\eta (1-\lambda )}{{(1-\lambda )}^2{\langle m\rangle }^2}+\frac{\eta }{{(1-\lambda )}^2{\langle m\rangle }^3},\hfill \end{array}$$

(7)

where $\langle m\rangle =\sqrt{\langle m_1\rangle \langle m_2\rangle }$ is the average number of detected photons in the absence of loss and $G_{\mu }^k={\prod }_{j=1}^k(j+\mu )/\mu$. For $\lambda =0$, $g^{12}=g^{21}$ and $g^{13}=g^{31}$. Quite recently [3], we have introduced a sufficient nonclassicality criterion, $B>1$, based on correlation functions up to the fourth order. In the case of asymmetric losses, the parameter B reads:

$$B={\langle m\rangle }^2(1-\lambda )\frac{g^{22}-{\left[g^{13}\right]}_s}{g^{11}}+\langle m\rangle \sqrt{(1-\lambda )}\frac{{\left[g^{12}\right]}_s}{g^{11}},$$

(8)

where ${\left[g^{jk}\right]}_s=(g^{jk}+g^{kj})/2$ is the symmetrized version of the $g^{jk}$ function. It can be demonstrated that there is a threshold value of $\lambda$ beyond which the inequality is no more satisfied and that this value increases at increasing the mean number of photons: the behaviour of this criterion is the opposite of the noise reduction factor.

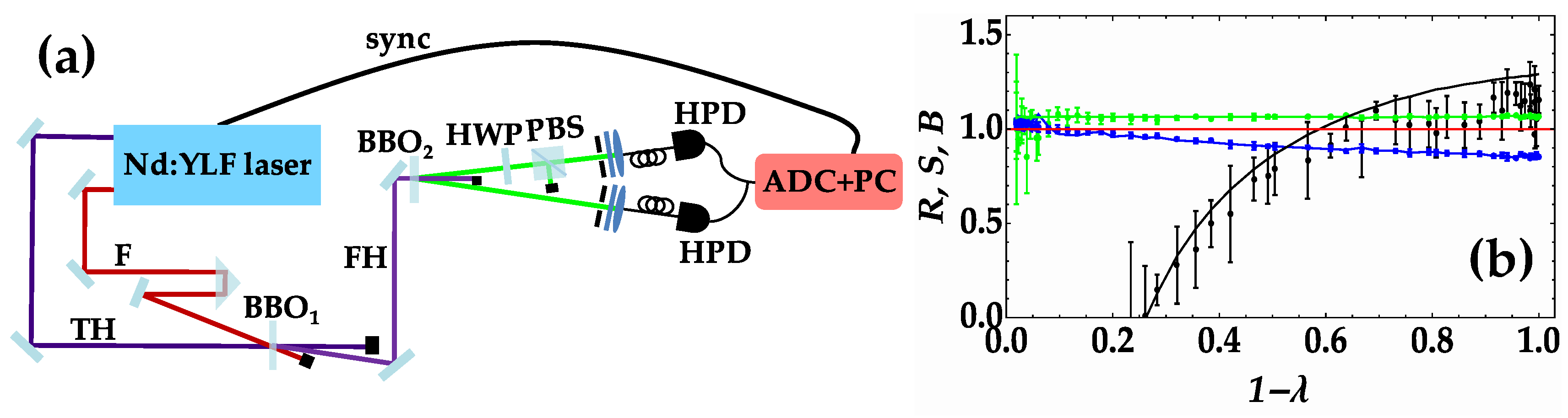
By exploiting the setup shown in the left panel of Figure 1 and described in Section 4, we generated a multi-mode TWB state in the mesoscopic intensity regime and used a pair of photon-number resolving detectors to measure the number of photons contained in every single pulse.

The right panel of Figure 1 displays the three inequalities introduced above as functions of $(1-\lambda )$, that is the fraction of photons surviving the asymmetric loss. The experimental data, shown as dots, are plotted together with the corresponding theoretical expectations evaluated in the experimental values of $\langle m_1\rangle$, $\langle m_2\rangle$, $\mu$, $\eta$ and $\lambda$. While the Schwarz inequality is always satisfied, thus proving the very quantum nature of TWB, the other two inequalities exhibit a threshold. $B>1$ is satisfied only for high values of $(1-\lambda )$, that is only for a small amount of loss. On the contrary, the NRF has a threshold for a high amount of loss.

3. Discussion

The three nonclassicality criteria introduced above exhibit different behaviors as a function of an asymmetric loss. In particular, the Schwarz inequality is satisfied for each value of $(1-\lambda )$, so that it cannot be used to highlight the presence of a disturbance in the transmission of the light signal. Viceversa, the fulfillment of the other two criteria depends on the value of the loss and there is a threshold value beyond which nonclassicality is not detected anymore. The threshold value behaves differently as a function of the mean number of photons in the twins beam, thus making the two criteria useful in different regimes. The nonclassicality criterion based on NRF is more robust at low intensity and it has been exploited in imaging protocols. In particular, the differential ghost-imaging protocols, both classical [7] and quantum [8], are the most demanding. In fact, for balanced loss, while the condition $R<1$ guarantees the quantum protocol a better signal-to-noise ratio, compared to the classical counterpart, $R<0.5$ is required to outperform the standard imaging with Poissonian light. The presence of an asymmetric loss tightens the requirements on R, which must be smaller at increasing values of $\lambda$. Also high-order correlations can be exploited for imaging [9,10] to achieve better signal-to-noise ratios. Work is in progress to demonstrate that the evaluation of the quantity B can be used to recover ghost images, with $B>1$ qualifying the quantumness of the employed resources. Finally, as a further step in the field of Quantum Communication, the data corresponding to different loss values can be suitably combined to simulate noisy channels characterized by specific statistical features [11].

4. Materials and Methods

According to the setup shown in the left panel of Figure 1, the fundamental and the third harmonic fields of a mode-locked Nd:YLF laser regeneratively amplified at 500 Hz produced the fourth harmonic (FH) at 262 nm in a type I $\beta$-Barium borate crystal (BBO${}_1$, cut angle = 37 deg, 8-mm long). The FH beam was used as pump field to generate a multi-mode TWB state by spontaneous parametric downconversion in a second type-I BBO crystal (BBO${}_2$, cut angle = 46.7 deg, 6-mm long). Two twin portions at frequency degeneracy, i.e., at 523 nm, were then spectrally and spatially filtered. We simulated the asymmetric lossy channel by inserting in one of the twin arms a half-wave plate (HWP) followed by a polarizing cube beam splitter (PBS). We changed the amount of loss by rotating the HWP by 50 deg in steps of 2 deg. For each angle, 100,000 acquisitions were performed. As the detectors we used two hybrid photodetectors (HPDs, mod. R10467U-40, Hamamatsu Photonics), whose outputs were amplified, synchronously integrated and digitized (ADC + PC). As already explained elsewhere [4], the detection apparatus can be calibrated in a self-consistent way by using the data corresponding to the same light under examination. In such a way, we have axcess to the shot-by-shot numbers of detected photons and we can thus investigate the statistical properties of light.