Machine Learning for Quantum Metrology ^†

Abstract

Phase estimation represents a significant example to test the application of quantum theory for enhanced measurements of unknown physical parameters. Several recipes have been developed, allowing to define strategies to reach the ultimate bounds in the asymptotic limit of a large number of trials. However, in certain applications it is crucial to reach such bound when only a small number of probes is employed. Here, we discuss an asymptotically optimal, machine learning based, adaptive single-photon phase estimation protocol that allows us to reach the standard quantum limit when a very limited number of photons is employed.

1. Introduction

Quantum metrology represents one of the most promising application of quantum theory. The aim in this context is to exploit quantum resources to measure an unknown physical quantity with better precision than any classical strategy [1]. In a general framework, this is achieved by preparing $\nu$-particle probes in an appropriate quantum state, leading to an improved sensitivity scaling as ${\nu }^{-1}$ (Heisenberg limit) with respect to the standard quantum limit (SQL) ${\nu }^{-1/2}$ that represents the ultimate bound for classical strategies that only allow the probes to interact with the target system once before measurement. Then, the process is repeated N times to acquire appropriate statistics on the parameter. A paradigmatic scenario to investigate the advantages of a quantum approach is provided by optical phase estimation [2], where the parameter to be estimated is a phase difference embedded within an interferometric setup. Several experiments have been reported, with a first unconditional violation of the standard quantum limit achieved recently in Ref. [3].

Most reported techniques and experiments that investigated phase estimation protocols have addressed the limit of a large number of probes $\nu$. In this asymptotic regime, general recipes have been defined that guarantee the capability to reach the ultimate precision bounds [4]. However, in several applications such as sampling in biological systems [5], it is crucial to optimally acquire information on the parameter by using only a limited amount of probes. To this end, a possible approach would involve the adoption of adaptive protocols, where the agent has access to a set of additional parameters that can be controlled during the estimation process. Such parameters (for instance, an additional phase) can be set to different values according to the knowledge acquired on the unknown parameter. To determine the optimal sequence of values for the additional parameters, machine learning techniques can represent a promising approach. Machine learning [6] is an emerging field which includes all those methods that are employed to make data-driven decisions. Recently, the application of such approach for quantum metrology has been suggested in Refs. [7,8,9].

Here, we discuss the application of machine learning techniques to design an optimal adaptive protocol based on Bayesian inference for single-photon phase estimation [10]. Such a protocol yields an unbiased estimate of the phase that saturates the standard quantum limit after a very limited number of probes. Finally, we conclude by discussing the possibility to extend machine learning based approaches in the multiparameter scenario and by adopting quantum states.

2. Results

In a phase estimation scenario, the aim is to measure a phase difference within an interferometric setup. The general strategy is to prepare an input N-photon probe state $\rho$. The prepared state is then sent through the interferometer, whose $\varphi$-dependent action can be parametrized by a unitary evolution $U_{\varphi }$. Information on the unknown phase is then encoded in the probe state ${\rho }_{\varphi }$, which is detected at the output according to a set of measurement operators ${\Pi }_x$. Such a process is then repeated $\nu$ times, leading to a final output string of outcomes $\mathbf{x}=(x_1,\dots ,x_{\nu })$. Finally, a suitable estimator function $\overline{\varphi }\left(\mathbf{x}\right)$ provides an estimate of the unknown phase.

Examples of commonly used estimators include the maximum likelihood estimator, which gives the unique unbiased estimate of the phase that is most likely to be correct given a uniform prior distribution over phase. We take a different approach here and instead use a Bayesian approach that explicitly tracks prior beliefs and use the posterior mean as our estimator instead. Within this approach, initial knowledge on the parameter is encoded in a probability distribution $P\left(\varphi \right)$ (prior distribution). Such knowledge is updated after each probe k according to the Bayes rule $P\left(\varphi \right|\{x_1,\dots x_k\})=P\left(x_k\right|\varphi )P\left(\varphi \right|\{x_1,\dots ,x_{k-1}\})/\mathcal{M}$, where $\mathcal{M}$ is a normalization factor, and $P\left(x\right|\varphi )$ is the likelihood function of the system. Bayesian protocols present several key characteristics. The most important characteristic is that they track prior beliefs about the estimated parameter. This ability not only means that information about the unknown phase can be easily used in the protocol, but also means that adaptive protocols can be easily developed and analyzed in this framework. Furthermore, since at the end of the estimation process the information is encoded in a probability distribution, it is possible to retrieve an estimate of the error in the parameter by calculating appropriate quantities (such as the variance) from $P\left(\varphi \right|\{x_1,\dots x_N\})$.

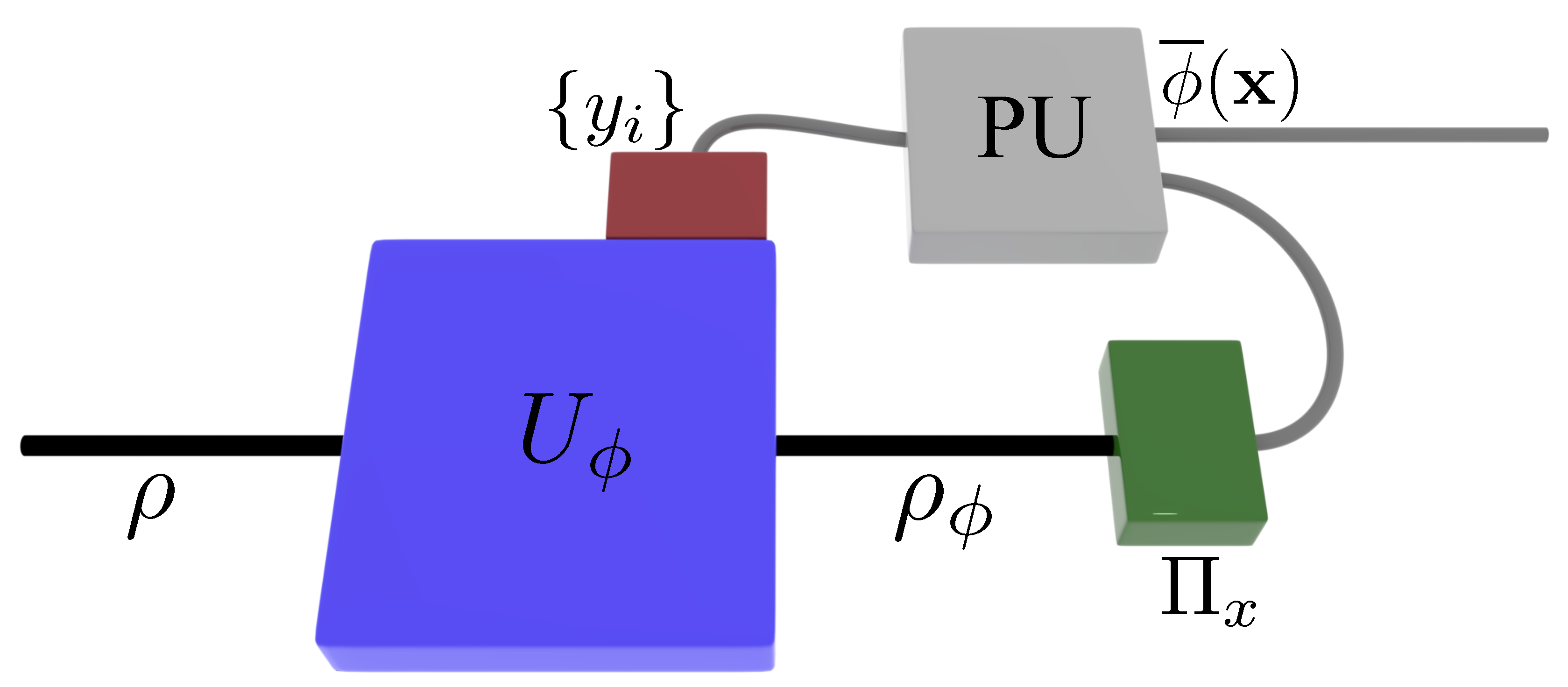
Let us now consider a generalized scheme shown in Figure 1. When additional parameters $\left\{y_i\right\}$ can be inserted within the evolution of the interferometer $U_{\varphi }$, the agent performing the estimation task has freedom of changing the value of these parameters at each step of the protocol to optimize the estimation process by using an adaptive approach. In this scenario, a crucial aspect is to find the optimal rule to decide how to tune at each step the values of parameters $\left\{y_i\right\}$. This is in general a complex task, since the agent has to choose from an exponentially increasing number of possible sequences of operations. Machine learning can then represent a powerful tool in this context, since it provides several optimization methods that can be employed for this task.

We have then devised [10] an optimal Bayesian protocol, named Gaussian Optimal (GO), to be applied in single-photon phase estimation ($\nu =1$). More specifically, we consider the case of a two-mode Mach-Zehnder interferometer, where the phase $\varphi$ between the arms is the unknown parameter. To perform adaptive strategies, a controlled phase shift $\Phi$ is introduced within the apparatus. At each step k of the protocol, the GO approach searches for the feedback phase value ${\Phi }_k$ that minimizes the variance for the next step. More specifically, the GO method assumes at step k a Gaussian prior $P\left(\varphi \right|\{x_1,\dots x_{k-1}\})\sim \mathcal{N}(\mu ,\sigma )$. Then, the processing unit computes the value of ${\Phi }_k$ to be applied that is expected to provide the minimum value of $V\left(\varphi \right)$, that is, the variance on the posterior $P\left(\varphi \right|\{x_1,\dots x_k\})$, averaged over all possible outcomes $x_k$. Such approach is guaranteed to be optimal (in terms of variance on the estimated parameter) when the assumption of a Gaussian prior is valid, which in general holds for $N\ge 5-10$. Furthermore, it can be shown that this method allows to reach the standard quantum limit $N^{-1/2}$ after a very limited number of probes have been employed [10].

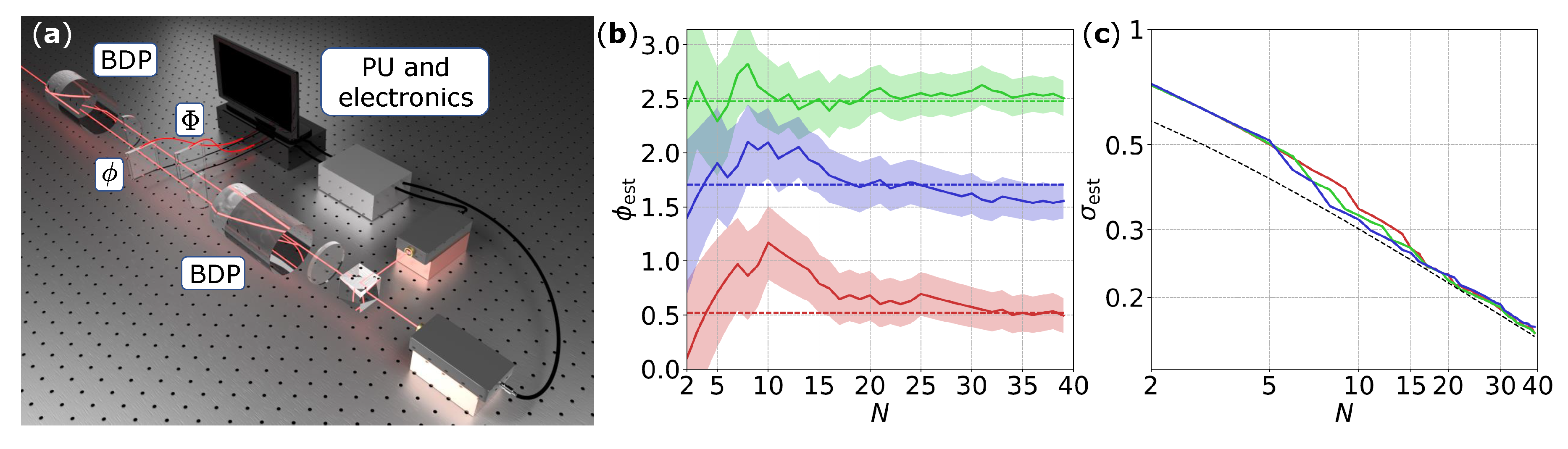
To verify the performances of the protocol, we performed an experimental test [10] in a two-mode interferometer injected by single photons. Input states have been prepared by means of the spontaneous parametric down-conversion process occurring in a nonlinear 2 mm long BBO crystal, injected by a $\lambda =392.5$ nm, 76 MHz repetition rate, 180 fs long pulsed laser beam. One of the two photons generated by the source is directly measured to herald the presence of the twin one, which is injected in the interferometer. The latter has been implemented by exploiting an intrinsically stable configuration (see Figure 2a) that does not require active stabilization mechanisms. The unknown phase $\varphi$ and the control phase $\Phi$ are tuned by two independent liquid crystal devices, whose action is determined by a processing unit (PU) that performs a completely automized control of the estimation process. More specifically, the value of $\Phi$ required for the adaptive protocol is calculated and set by the PU during the acquisition process after each event by following the GO rule outlined above. The experimental results for different values of the phases are shown in Figure 2b,c. The starting point of each estimation process is a uniform prior $P\left(\varphi \right)={\left(2\pi \right)}^{-1}$, quantifying the absence of a priori knowledge on the parameter. We observe that the algorithm converges to the true value and approaches the standard quantum limit after a very limited number of probes ($N\sim$ 10–15). Furthermore, the perfomances are analogous for different values of the phases, thus allowing the protocol to be independent from the phase value.

3. Discussion

In this paper we have discussed the development and the experimental implementation of a machine learning approach for adaptive single-photon phase estimation protocols. Such approach is an online method based on Bayesian inference that calculates the optimal value for the control phase to be applied at each step of the protocol. By using this approach, it is possible to reach the ultimate bound, provided in this case by the standard quantum limit, after a very limited number of probes. Several open perspectives can be envisaged starting from these results. Our approach is able to optimally extract the information on the unknown parameter can be combined with finite size analysis [11,12] of the ultimate bounds. On the other hand, generalization of this work can be found in different directions. These include the adoption of quantum resources as input states, where machine learning driven adaptive approaches can be a significant tool to obtain quantum-enhanced performances with limited number of probes. Furthermore, another relevant direction is the extension of this approach to the multiparameter case [13,14,15]. Furthermore, the application of different machine learning techniques can be investigated to identify the most appropriate one depending on the configuration.