The Friedrichs-Lee Model and Its Singular Coupling Limit ^†

Abstract

Lee’s field-theoretical model describes the interaction between a qubit and a structured bosonic field. We study the mathematical properties of the Hamiltonian of the single-excitation sector of the theory, including a possibly “singular” qubit-field coupling (i.e., mediated by a non-square integrable form factor). This result allows for a rigorous description of qubit-field interactions in many physically interesting systems and may be extended to higher-excitation sectors of the theory.

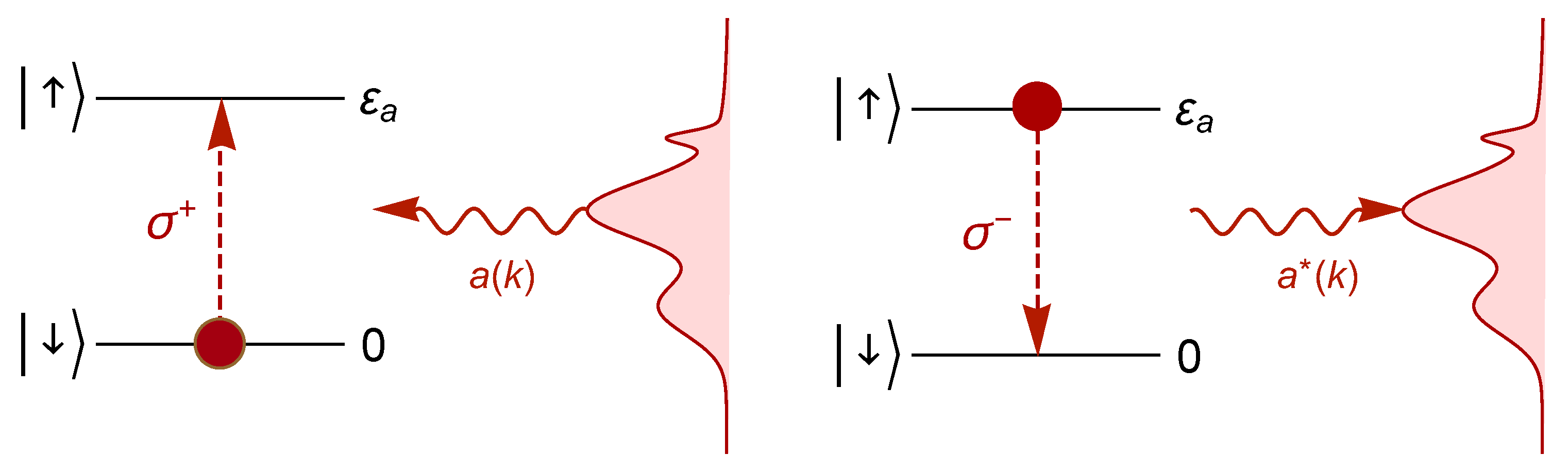
1. Introduction

Consider a two-level quantum system with ground and excitation energies equal to 0 and ${\epsilon }_{\mathrm{a}}$, respectively, and a bosonic field with momentum space given by some measure space $(X,\mathrm{d}\mu )$, where the measure $\mu$ contains all information about the field structure. The Hamiltonians which describe the qubit and the field are

$$H_{\mathrm{qubit}}={\epsilon }_{\mathrm{a}}|\uparrow ⟩⟨\uparrow |,$$

(1)

$$H_{\mathrm{field}}={\int }_X\omega \left(k\right)a^{†}\left(k\right)a\left(k\right)\mathrm{d}\mu ,$$

(2)

with $|\uparrow ⟩$, $|\downarrow ⟩$ being the excited and ground states of the qubit, $\omega \left(k\right)$ being the boson dispersion relation, and $a\left(k\right)$, $a^{†}\left(k\right)$ being annihilation and creation operators satisfying the canonical commutation relations $[a\left(k\right),a^{†}\left(k^{\prime }\right)]=\delta (k-k^{\prime })$ and $[a\left(k\right),a\left(k^{\prime }\right)]=[a^{†}\left(k\right),a^{†}\left(k^{\prime }\right)]=0$. Lee’s interaction Hamiltonian between the qubit and the field reads [1]

$$V_g={\int }_X\left({\sigma }^{+}\otimes \overline{g\left(k\right)}a\left(k\right)+{\sigma }^{-}\otimes g\left(k\right)a^{†}\left(k\right)\right)\mathrm{d}\mu ,$$

(3)

with $g\in L^2(X,\mathrm{d}\mu )$ being the form factor of the interaction, ${\sigma }^{+}=|\uparrow ⟩⟨\downarrow |$ and ${\sigma }^{-}=|\downarrow ⟩⟨\uparrow |$; its action is represented in Figure 1. Lee’s Hamiltonian $H_{\mathrm{L}}=H_{\mathrm{qubit}}+H_{\mathrm{field}}+V_g$ preserves the total number of excitation

$$N={\int }_X{a}^{†}\left(k\right)a\left(k\right)\mathrm{d}\mu +|\uparrow ⟩⟨\uparrow |,$$

(4)

and hence we can consider its restriction to any sector with a fixed number of excitation. We will focus on the one-excitation sector, $N=1$, whose generic normalised state can be written as

$$\mathsf{\Psi }=\left(\begin{array}{c}x\\ \xi \end{array}\right),x\in \mathbb{C},\xi \in L^2{(X,\mathrm{d}\mu ),\left|x\right|}^2+{\int }_X{\left|\xi \left(k\right)\right|}^2\mathrm{d}\mu =1,$$

(5)

Figure 1. Schematic representation of the allowed qubit-field interactions in the theory.

$\xi$ being the boson wave function in the momentum space and x being the probability amplitude of the excited state of the qubit. In particular, the vector

$${\mathsf{\Psi }}_0=\left(\begin{array}{c}1\\ 0\end{array}\right)$$

(6)

corresponds to the state in which the field is in the vacuum state and the qubit is excited.

The restriction of the Lee Hamiltonian to this sector, first studied in [2], will be referred to as the Friedrichs-Lee Hamiltonian $H_{\mathrm{FL}}$, and its action can be written in matrix form:

$$H_{\mathrm{FL}}=\left(\begin{array}{cc}{\epsilon }_{\mathrm{a}}& ⟨g|\\ g& \Omega \end{array}\right),$$

(7)

with $\Omega$ being the multiplication operator by the function $\omega \left(k\right)$, $\Omega \xi \left(k\right)=\omega \left(k\right)\xi \left(k\right)$. The domain of $H_{\mathrm{FL}}$ is the set of all states (5) with boson wave function $\xi$ in the domain $D\left(\Omega \right)$ of $\Omega$, i.e., such that ${\int }_X{\left|\omega \left(k\right)\xi \left(k\right)\right|}^2\mathrm{d}\mu <\infty$: physically, this means that states with finite variance of the full (qubit+field) energy are all the states with finite variance of the field energy.

However, many cases of physical interest cannot be consistently described by a square-integrable form factor, $g\in L^2(X,\mathrm{d}\mu )$. Two notable examples:

• No square-integrable form factor implementing an exponential decay of the survival probability of ${\mathsf{\Psi }}_0$ exists, since ${\mathsf{\Psi }}_0$ is in the domain of the Hamiltonian [3,4]. An exponential decay can be formally obtained e.g. in a one-dimensional setting $(X,\mathrm{d}\mu )=(\mathbb{R},\mathrm{d}k)$, with $\omega \left(k\right)=k$ and $g\left(k\right)=1$, but such a form factor obviously fails to be square-integrable;
• The standard choices of parameters in waveguide QED (see e.g., [5]) are

  $$\omega \left(k\right)=\sqrt{k^2+m^2},g\left(k\right)=\frac{1}{\sqrt[4]{k^2+m^2}},$$

  (8)
  m being the effective photon mass; the form factor g fails to be square-integrable because of its behaviour at large momenta $\left|k\right|$ (UV divergence).

We will show that the model (7) can be extended in such a way that a proper class of singular couplings can be included; besides, its spectrum and resonances can be completely characterised. This accounts for a systematic study of bound states, scattering states and resonances in many physical systems.

2. Singular Coupling

Let $\mathcal{H}=L^2(X,\mathrm{d}\mu )$, and define, for any $s>0$, the space of functions

$${\mathcal{H}}_{-s}=\left\{g:X\to {\mathbb{C}|\parallel g\parallel }_{-s}:={\int }_X\frac{{\left|g\left(k\right)\right|}^2}{{\left(\left|\omega \right(k\left)\right|+1\right)}^s}\mathrm{d}\mu <\infty \right\};$$

(9)

${\left\{{\mathcal{H}}_{-s}\right\}}_{s\ge 0}$, each endowed with the norm ${\parallel ·\parallel }_{-s}$, is known to be a “scale” of Banach spaces. i.e., with ${\mathcal{H}}_{-s}\supset {\mathcal{H}}_{-s^{\prime }}$ for every $s>s^{\prime }$, every inclusion being dense with respect to the topology of the smaller space (see e.g., [6]).

The case $s=2$ is of particular interest for our purposes: indeed, given $g\in {\mathcal{H}}_{-2}$, we have $\frac{1}{{\omega }^2+1}g\in \mathcal{H}$, and using this property we can prove that a generalized Friedrichs-Lee Hamiltonian can be defined for a singular coupling $g\in {\mathcal{H}}_{-2}$ [7]:

Theorem 1.

Let $\epsilon \in \mathbb{R}$, $g\in {\mathcal{H}}_{-2}$, and consider an operator $H_{g,\epsilon }$ with domain

$$D\left(H_{g,\epsilon }\right)=\left\{\left(\begin{array}{c}x\\ \xi -x\frac{\omega }{{\omega }^2+1}g\end{array}\right)|x\in \mathbb{C},\xi \in D\left(\Omega \right)\right\}$$

(10)

such that

$$H_{g,\epsilon }\left(\begin{array}{c}x\\ \xi -x\frac{\omega }{{\omega }^2+1}g\end{array}\right)=\left(\begin{array}{c}\epsilon x+⟨g|\xi ⟩\\ \omega \xi +x\frac{1}{{\omega }^2+1}g\end{array}\right).$$

(11)

Then $H_{g,\epsilon }$ is self-adjoint and, if $g\in \mathcal{H}$, $H_{g,\epsilon }$ coincides with a Friedrichs-Lee Hamiltonian $H_{\mathrm{FL}}$ in (7) with form factor g and excitation energy

$${\epsilon }_{\mathrm{a}}\left(g\right)=\epsilon -{\int }_X\frac{\omega \left(k\right)}{\omega {\left(k\right)}^2+1}{\left|g\left(k\right)\right|}^2\mathrm{d}\mu .$$

(12)

Moreover, if $Q\left(H_{g,\epsilon }\right)\supset D\left(H_{g,\epsilon }\right)$ is the form domain of $H_{g,\epsilon }$ (i.e., the space of vectors with finite mean energy, but possibly infinite variance) then the following characterisation holds:

• $g\in \mathcal{H}\iff {\mathsf{\Psi }}_0\in D\left(H_{g,\epsilon }\right)$;
• $g\in {\mathcal{H}}_{-1}\setminus \mathcal{H}\iff {\mathsf{\Psi }}_0\in Q\left(H_{g,\epsilon }\right)\setminus D\left(H_{g,\epsilon }\right)$;
• $g\in {\mathcal{H}}_{-2}\setminus {\mathcal{H}}_{-1}\iff {\mathsf{\Psi }}_0\notin Q\left(H_{g,\epsilon }\right)$,

and, for $g\in {\mathcal{H}}_{-1}$, $⟨{\mathsf{\Psi }}_0|H_{g,\epsilon }{\mathsf{\Psi }}_0⟩={\epsilon }_{\mathrm{a}}\left(g\right)$, with ${\epsilon }_{\mathrm{a}}\left(g\right)$ as in Equation (12).

Notice that a domain change has been performed: in order to obtain a well-defined operator up to $g\in {\mathcal{H}}_{-2}$, a “singular term” $x\frac{\omega }{{\omega }^2+1}g$—which is outside the domain $D\left(\Omega \right)$ whenever $g\notin \mathcal{H}$—must be subtracted to the boson wave function $\xi$ in (10). This also causes a change of the energy parameter of the qubit from ${\epsilon }_{\mathrm{a}}\left(g\right)$ to $\epsilon$: physically, $\epsilon$ can be interpreted as the “dressed” excitation energy of the qubit, as opposed to the “bare” one ${\epsilon }_{\mathrm{a}}\left(g\right)$. It is important to note that, in the most singular case $g\in {\mathcal{H}}_{-2}\setminus {\mathcal{H}}_{-1}$, the qubit bare energy ${\epsilon }_{\mathrm{a}}\left(g\right)$is not well defined at all, since the integral in Equation (12) diverges; this is due to the fact that ${\epsilon }_{\mathrm{a}}\left(g\right)$ is the mean energy of ${\mathsf{\Psi }}_0$, which however diverges when $g\in {\mathcal{H}}_{-2}\setminus {\mathcal{H}}_{-1}$. These results are summarized in Table 1.

Table 1. Mean value and variance of the total energy of the state ${\mathsf{\Psi }}_0$ for the three classes of coupling described in the theorem.

Coupling		${⟨{\mathit{H}}_{\mathit{g},\mathit{\epsilon }}⟩}_{{\mathit{\Psi }}_0}$		${⟨{\mathit{H}}_{\mathit{g},\mathit{\epsilon }}^2⟩}_{{\mathit{\Psi }}_0}-{⟨{\mathit{H}}_{\mathit{g},\mathit{\epsilon }}⟩}_{{\mathit{\Psi }}_0}^2$
$g\in \mathcal{H}$		${\epsilon }_{\mathrm{a}}\left(g\right)$		${\parallel g\parallel }^2$
$g\in {\mathcal{H}}_{-1}\setminus \mathcal{H}$		${\epsilon }_{\mathrm{a}}\left(g\right)$		∞
$g\in {\mathcal{H}}_{-2}\setminus {\mathcal{H}}_{-1}$		∞		∞

Moreover, one can prove that a singular coupling can be obtained as the limit of square-integrable form factors [7]:

Theorem 2

(Singular coupling limit). For every singular (i.e., $g\notin \mathcal{H}$) Friedrichs-Lee Hamiltonian (11), there is a sequence ${\left(g_n\right)}_{n\in \mathbb{N}}\subset \mathcal{H}$ such that $H_{g_n,\epsilon }$ converges to $H_{g,\epsilon }$ in the norm resolvent sense. Conversely, given a sequence ${\left(g_n\right)}_{n\in \mathbb{N}}\subset \mathcal{H}$ and some $g\in {\mathcal{H}}_{-2}$, if $\parallel g_n{-g\parallel }_{-2}\to 0$, then $H_{g_n}\to H_g$ in the norm resolvent sense.

Therefore, the absence of a well-defined bare excitation energy for the qubit can be physically interpreted as the consequence of a renormalisation procedure, and $\epsilon$ as a renormalized energy. Indeed, Equation (12) implies

$${\epsilon }_{\mathrm{a}}\left(g_n\right)=\epsilon -{\int }_X\frac{\omega \left(k\right)}{\omega {\left(k\right)}^2+1}{\left|g_n\left(k\right)\right|}^2\mathrm{d}\mu ,$$

(13)

but the integral diverges as $n\to \infty$ whenever $g\in {\mathcal{H}}_{-2}\setminus {\mathcal{H}}_{-1}$ and hence, being $\epsilon$ fixed, the bare excitation energy ${\epsilon }_{\mathrm{a}}\left(g_n\right)$ diverges as well; in other words, if we keep the dressed excitation energy of our model finite, the bare energy must diverge.

3. Conclusions

We have constructed a Hamiltonian model which allows for a rigorous description of the single-excitation interaction between a qubit and a bosonic field, which includes a large class of singular coupling, and we have classified the form factors by the energy properties of the vacuum state ${\mathsf{\Psi }}_0$. The extension to singular couplings requires a domain change, which implies, on the physical level, that the field energy of the boson component must have infinite variance, and in some case infinite mean value, in order for the variance of the whole qubit-field system to be finite; an operator-theoretical renormalisation procedure is also involved.

The model is self-consistent and its spectral properties can be studied in full generality [7]; the extension to an arbitrary number of qubits is straightforward and may be applied to many systems of physical interest. Finally, the strategy of including singular couplings through a domain change and a renormalisation of the excitation energies might be extended to Lee’s field theory, and pave the way to a new approach to renormalisation of quantum field theories.