Parity Doubling in QCD Thermodynamics ^†

Abstract

Motivated by the recent lattice study by FASTSUM collaboration, effective masses of the baryon parity-doublers are shown for various pion masses. A general trend of the nucleon and delta parity-doublers is consistent with the lattice Quantum Chromodynamics (QCD) observation, whereas the hyperon masses exhibit a qualitatively different behavior, traced back to the lattice set-up with the heavy pion comparable to the kaon. As an application to hot QCD, we demonstrate the fluctuations and correlations involving baryon number in hot hadronic matter with modified masses of negative-parity baryons, in the context of the hadron resonance gas. Confronting the baryon number susceptibility, baryon–charge and baryon–strangeness correlations as well as their ratios with the lattice QCD data for the physical pion mass, we find that the strong downward mass shift in the hyperons can accidentally reproduce some correlation ratios, however it also tends to overshoot the individual fluctuations and correlations of lattice simulations. Another application of nucleon parity doubling is the physics of neutron stars. Under beta equilibrium and charge neutrality, hadronic matter with unbroken chiral symmetry can be favored in the core of the neutron stars.

1. Introduction

Spectral properties of hadrons are expected to change in a medium. A search for those modifications because of partial restoration of the chiral symmetry has been one of the central subjects in heavy-ion collisions where hot and/or dense matter is supposed to be created. Substantial medium modifications of the lowest-lying hadrons have been predicted in a large class of chiral models, whereas their reliable estimates in lattice QCD are thus far limited to the screening masses. Recently, the thermal masses of non-strange and strange baryons with positive and negative parity have been extracted from the temporal correlation functions by the FASTSUM collaboration [1,2]. The negative-parity states clearly show downward mass shifts, whereas the positive-parity baryons are rather insensitive to temperature. The obtained spectra follow qualitatively an expectation from parity doubling of the chiral symmetry, indicating that the states with the same spin but opposite parity tend to become degenerate when the symmetry gets partially restored.

In this contribution, we briefly summarize our recent study on the thermodynamics of parity doubling: the in-medium masses of baryon octet and decuplet and their potential influence over fluctuations and correlations in the context of a chiral effective theory [3] and in-medium Hadron Resonance Gas (HRG) model [4,5], as well as the physics of neutron stars in a hybrid approach for hadrons and quarks [6].

2. Parity Doubling

The baryon octet and decuplet with opposite parity can be modeled in an effective chiral approach with $N_f=2+1$ [3], where the masses are described as certain functions of the light-quark ${\sigma }_q$ and strange-quark ${\sigma }_s$ condensates as well as the degenerate mass of parity doublers $m_0$, which is not anchored to dynamical chiral symmetry breaking. Their modifications are therefore driven entirely by the in-medium quark condensates. We use the thermal profiles of the condensates for the physical pion and kaon masses measured at $0.6<T/T_c<1.2$ in lattice QCD by the HotQCD collaboration [7].

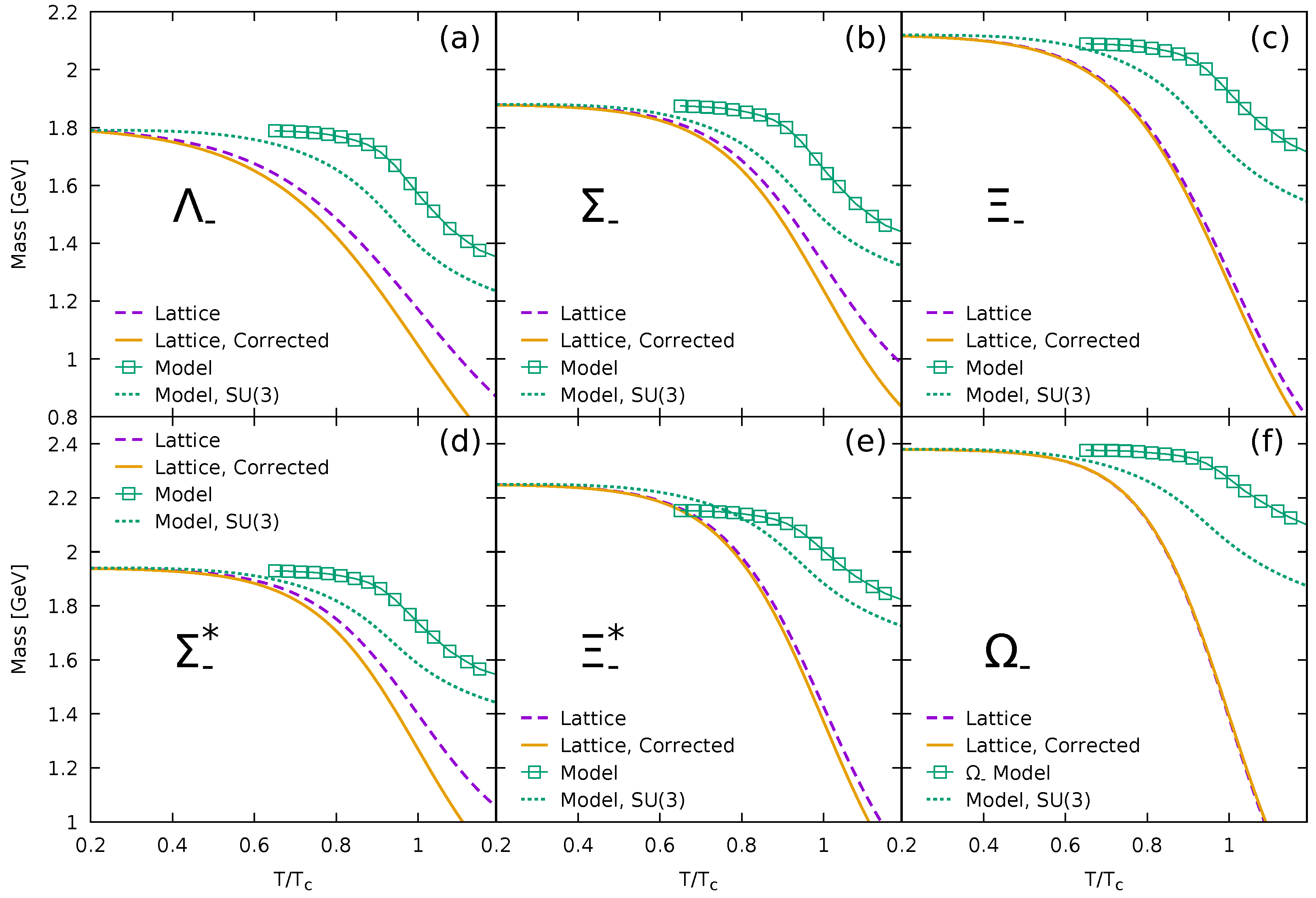
In Figure 1, we present the results from this effective chiral model as well as the masses based on a parameterization motivated by the lattice results in [1,4].

$$\begin{array}{ccc}\hfill M_{-}^i\left(T\right)& =& M_{-}^i(T=0)\omega (T,b_i)+M_{-}^i\left(T_c\right)(1-\omega (T,b_i)),\hfill \\ \hfill \omega (T,b_i)& =& tanh[(1-T/T_c)/b_i]/tanh(1/b_i),\hfill \end{array}$$

(1)

for a given baryonic state i with negative parity, and with $M_{-}^i\left(T_c\right)$ and $b_i$ the fitting parameters to be fixed for each channel. The data are given as a function of $T/T_c$; the value of $T_c$ does not affect the fit but later it is set to the physical value of 154 MeV. The parameter $b_i$ corresponds to the width of the chiral crossover. A complete set of those values is given in

Table 1. Assignment of the negative-parity states in in-medium HRG [5].

P${}^{-}$ State	N	$\mathbf{\Lambda }$	$\mathbf{\Sigma }$	$\mathbf{\Xi }$	$\mathbf{\Delta }$	${\mathbf{\Sigma }}^{*}$	${\mathbf{\Xi }}^{*}$	$\mathbf{\Omega }$
Mass LGT [1,4]	1779	1899	1823	1917	2138	2131	2164	2193
$M_{-}^i\left(T_c\right)$ [MeV]	1254	1172	1329	1295	1405	1398	1426	1383
$b_i$	0.338	0.369	0.257	0.275	0.312	0.257	0.246	0.213
Assignment A	1535	1405	1750	1690	1700	1670	1820	2250
Assignment B	1535	1670	1750	1950	1700	1940	1820	2250
Mass [MeV]	1535	1790	1880	2090	1710	1930	2150	2380
Assignment C	1535	1800	1880	2120	1700	1940	2250	2380

.

We note that the simulations [1,2] were performed for heavier light-quark mass than the physical one, leading to $m_{\pi }=384$ MeV, whereas the strange quark is set to the physical one. To correct the unphysical effect from the heavy up and down quarks, $M_{-}^i(T=0)$ is set to its PDG value in the following calculation. We need to correct the value of $M_{-}\left(T_c\right)$ as well and re-scale it by multiplying the factor $M_{+}^{\mathrm{PDG}}(T=0)/M_{+}^{\mathrm{lattice}}(T=0)$ with $M_{-}\left(T_c\right)$. It is uncertain how to assign the negative-parity states to the observed ones because of unknown quantum numbers of some of the candidates. In fact, one finds, e.g. three low-lying Lambda baryons with negative parity on the PDG table: ${\mathrm{\Lambda }}_{-}\left(1405\right),{\mathrm{\Lambda }}_{-}\left(1670\right),{\mathrm{\Lambda }}_{-}\left(1800\right)$. Hence, we follow the suggestion in [4] (Set C) and further adopt two different assignments, Sets A and B. Set A includes the lighter state for ${\mathrm{\Lambda }}_{-}$, ${\mathrm{\Xi }}_{-}$, and ${\mathrm{\Sigma }}_{-}^{*}$ while Set B the heavier ones.

When the $SU\left(3\right)$ limit with a common quark-mass is taken, the chiral model yields a quite similar trend to the lattice observation up to $T_c$. In the realistic setup with the physical $m_{\pi }$, one observes a sizable difference between the model and Equation (1), which sets in at a rather low temperature, $T/T_c\sim 0.6$. The distinct features are understood as remnants of the underlying flavor symmetries and their universality [3]; the $SU\left(3\right)$ leads to a first-order chiral phase transition, whereas the $SU\left(2\right)$ to a second-order. The physics with $N_f=2+1$ near $T_c$ is to a large extent governed by the $O\left(4\right)$ universality class, so that such a drastic decrease based on Equation (1) is rather an $SU\left(3\right)$ artifact and would not be expected in the realistic QCD thermodynamics.

This becomes more striking in strange baryons. The hyperon masses from the chiral model and from Equation (1) are shown in Figure 2. It is clearly seen that the discrepancy increases with larger strangeness. It would be intriguing to confirm whether such a strong mass-reduction of the hyperons still persists in simulations with a lighter pion.

3. Fluctuations and Correlations

In Ref. [4], the observed medium modification was used to possibly explain a missing contribution in correlations among the conserved charges, in the context of the in-medium Hadron Resonance Gas (HRG) model. In the following, we examine the fluctuations and correlations of the net-baryon with net-charge and net-strangeness on the basis of the standard HRG, the in-medium HRG and the chiral approach [5]. In particular, we focus on the quantities ${\chi }_2^B$, ${\chi }_{11}^{BQ}$, and ${\chi }_{11}^{BS}$ at ${\mu }_B={\mu }_Q={\mu }_S=0$. Since mesons do not contribute to those susceptibilities, they are good measures of in-medium effects in the baryonic sector. We neglect an intrinsic chemical-potential dependence in the baryon masses in the present calculations for simplicity, which is well justified at small chemical potential.

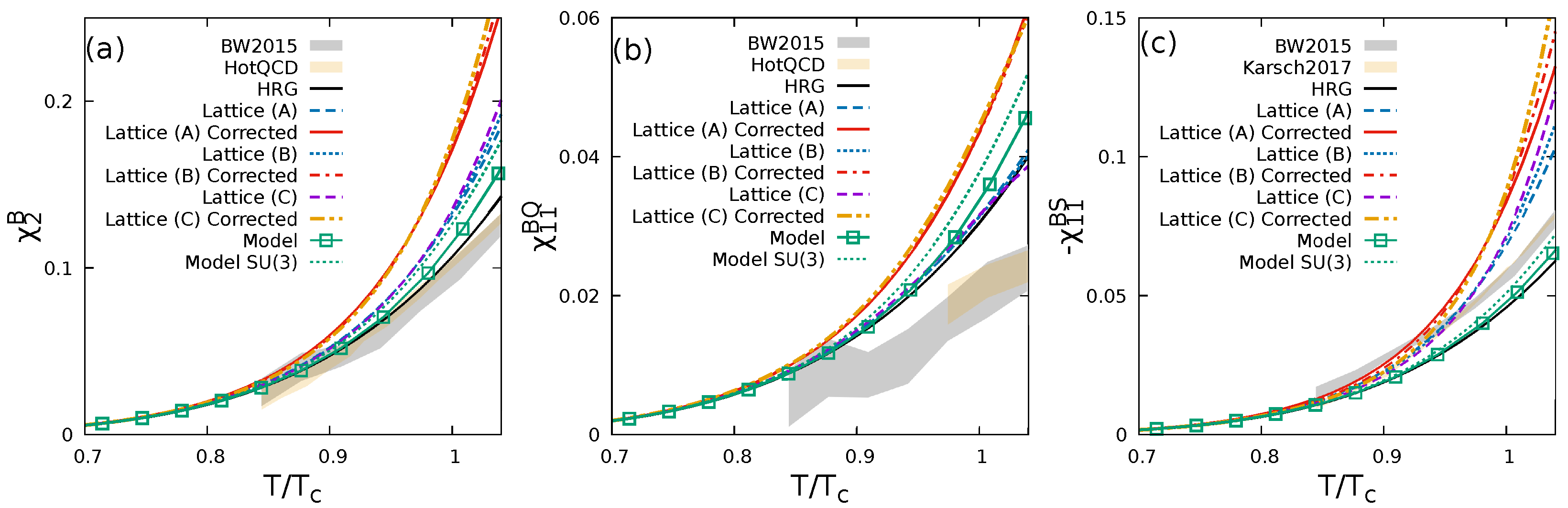
By the standard thermodynamic calculations, we obtain the thermal properties of the ${\chi }_2^B$, ${\chi }_{11}^{BQ}$ and $-{\chi }_{11}^{BS}$, as shown in Figure 3.

The in-medium HRG apparently overshoots individual susceptibilities of lattice QCD because of the strong decrease in the masses of the negative-parity states. We see a moderate enhancement in all the three assignments, Lattices with assignments A, B and C in Table 1, and it becomes stronger when $M\left(T_c\right)$ is corrected, since the correction further reduces the masses near $T_c$. The results from the chiral effective model follows the same trend, but the amount of the enhancement is much smaller than the tanh-parameterization (Equation (1)), because of the much weaker mass shifts particularly in the hyperon sectors.

In Figure 4, we present the ratios ${\chi }_{11}^{BQ}/{\chi }_2^B$ and $-{\chi }_{11}^{BQ}/{\chi }_{11}^{BS}$ together with corresponding lattice results.

The results with Lattices (A) and (B) follow the trend seen in the HotQCD data. As becomes clear in Figure 3, however, the individual susceptibilities cannot be reproduced by the in-medium HRG. The coincidence comes from the strong mass reduction in the charge asymmetric states. The chiral approach leads to the opposite trend that the ratio is above the standard HRG, due to the much milder mass-reduction in the hyperon sector. Therefore, we conclude that the lattice data cannot be explained solely by the mass reduction of the negative-parity baryons.

4. The Structure of Neutron Stars

Parity doubling is expected to play a central role in cold but dense matter as well. We recently applied the chiral effective model with nucleon parity doubling to the physics of neutron stars under $\beta$ equilibrium and charge neutrality [6]. We utilize a hybrid model where both quarks and hadrons are treated as dynamical degrees of freedom together with a mechanism to suppress the quarks (nucleons) at low (high) density [11,12]. The model yields the chiral symmetry restoration as a first-order, a second-order phase transition or a smooth crossover, depending on two major parameters; one is the degenerate mass of nucleon parity doublers with restored chiral symmetry, $m_0$, and the other is the infra-red cutoff of the quark thermal distribution function in matter-free space, $\alpha b_0$ [11]. The most characteristic feature is that at increasing baryon density, the chiral symmetry is restored within the hadronic phase by lifting the mass splitting between chiral partner states, before quark deconfinement takes place, as depicted in Figure 5 where the energy–density profiles of the stars are shown as a function of the radius.

The two parameters $m_0$ and $\alpha b_0$ can be restricted by imposing the following astrophysical constraints:

• The maximum mass of the neutron stars [13];
• the onset of the direct Urca process relevant for the cooling of neutron stars [14,15]; and
• the dimensionless tidal deformability in the binary merger [16].

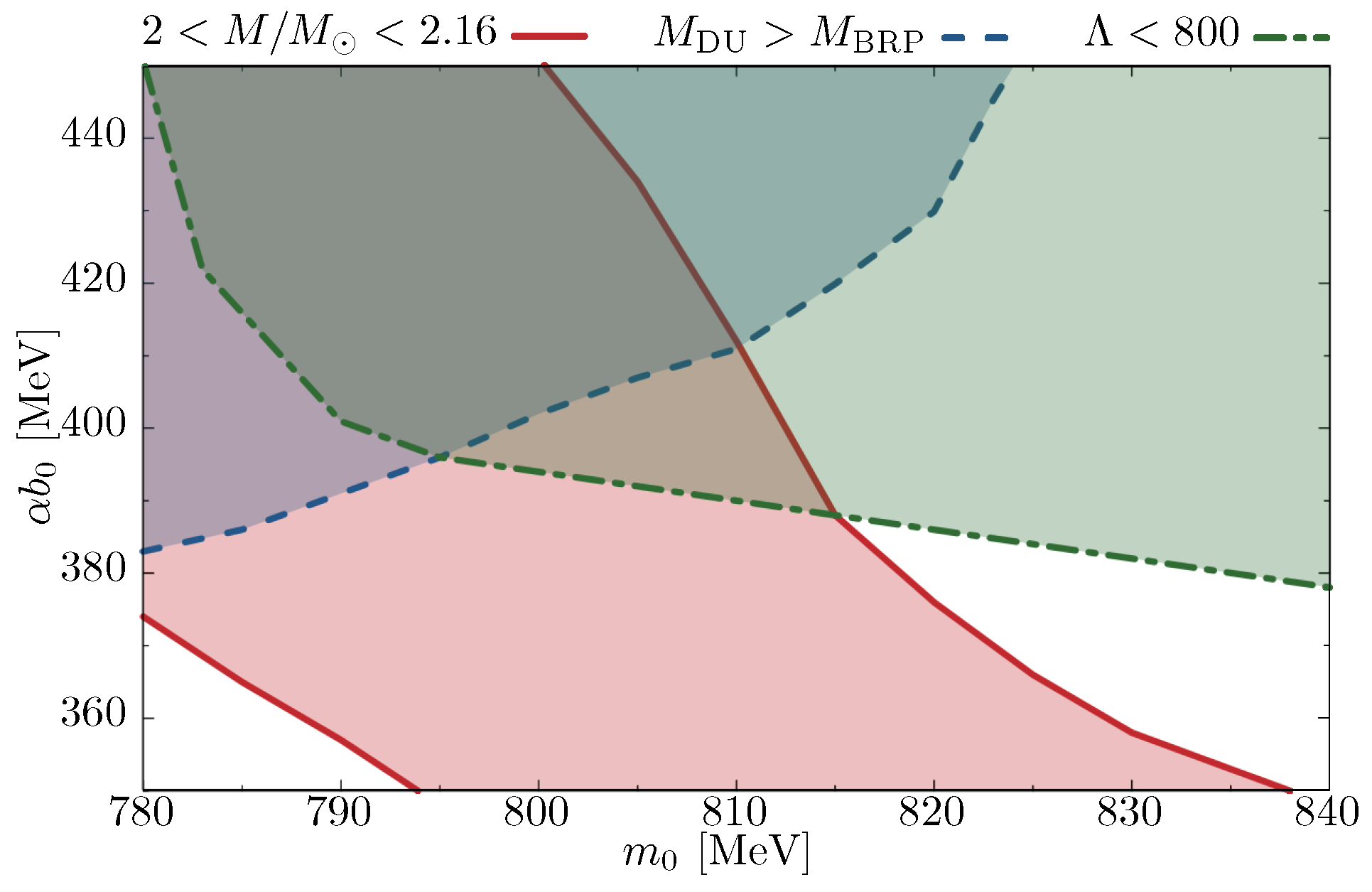
In Figure 6, we compile those three constraints in the $(\alpha b_0,m_0)$-plane.

The region where they overlap gives the most preferable sets of the parameters.

The observational neutron-star data provide useful constraints on the structure of strongly interacting matter. They may constrain the phase diagram of isospin-symmetric QCD matter, which is of major relevance for the heavy-ion physics. In Figure 7, we show the phase diagram obtained in the model in the $(T,{\mu }_B)$-plane, for the case of $m_0=790$ MeV and various values of $\alpha b_0$.

In view of the constraints given in Figure 6, the scenarios with $\alpha b_0=350$ MeV and $\alpha b_0=370$ MeV are rather excluded. Hence, either rather low temperature for the critical end point or even its absence in the phase diagram for isospin-symmetric matter is favored.

5. Conclusions

Motivated by the recent lattice QCD result on the baryon-octet and -decuplet masses at finite temperature, we formulated thermal masses of baryon parity doublers as functions of the chiral order parameter. We examined the consequences of several scenarios with in-medium masses for the negative-parity octet and decuplet baryons, adopting a lattice-motivated parameterization and that from a chiral effective theory. We showed that the reproduction of the lattice QCD results of the ratios ${\chi }_{11}^{BQ}/{\chi }_2^B$ and $-{\chi }_{11}^{BQ}/{\chi }_{11}^{BS}$ is rather accidental when the in-medium masses are naively introduced in the conventional HRG approach. Since the strong mass shifts of the hyperons observed by FASTSUM is a consequence of the approximate flavor $SU\left(3\right)$ due to a heavy pion mass, it is critical to confirm if the large hyperon mass-shift persists for the physical pion mass.

We emphasize that the treatment of the resonances in the conventional HRG model is insufficient and a proper inclusion of the widths improves the thermodynamics (see, e.g., [17]). Hence, our results do not rule out the manifestation of parity doubling. To correctly account for the influence of the chiral symmetry restoration over the thermodynamic quantities, a consistent framework beyond the mass shifts is required.

We also presented the consequences of a recently developed model for the equation of state of dense QCD matter under neutron-star conditions and the phenomenology of compact stars. It was shown that the chiral symmetry restoration by parity doubling within the hadronic phase can be archived in the core of massive neutron stars. The high-mass stars, such as the PSR J0348 + 0432 pulsar with the mass $2.01\left(4\right)M_{\odot }$, can be realized in three different ways: (1) single-phase nuclear matter with broken chiral symmetry; (2) its core is made of a mixed phase surrounded by chirally broken and confined nuclear matter; or (3) two-phase nuclear matter where the core with restored chiral symmetry but still confined is surrounded by chirally broken and confined matter.