Continuous and Pulsed Quantum Control †
Abstract
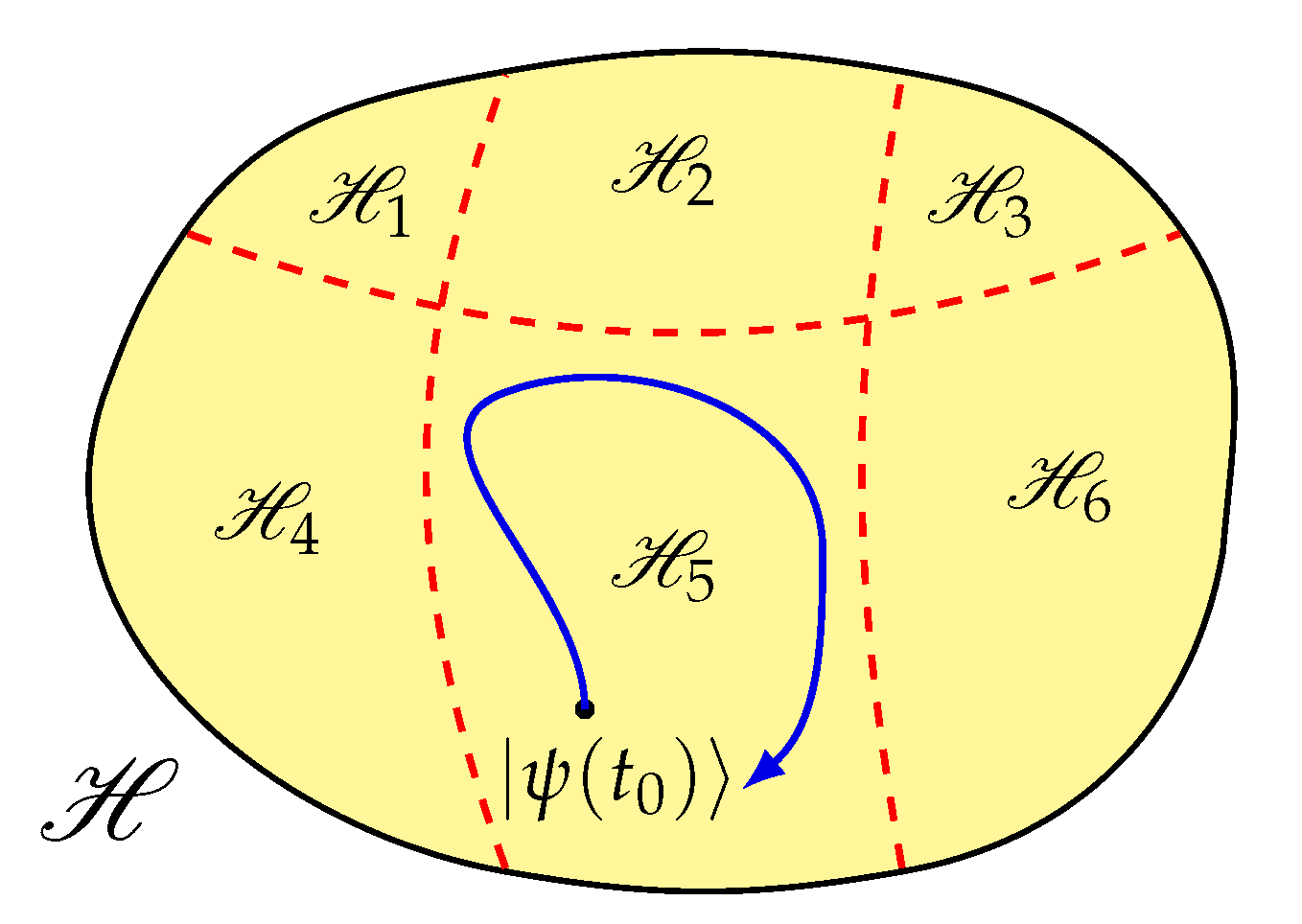
:1. Introduction
2. Strong Continuous Coupling
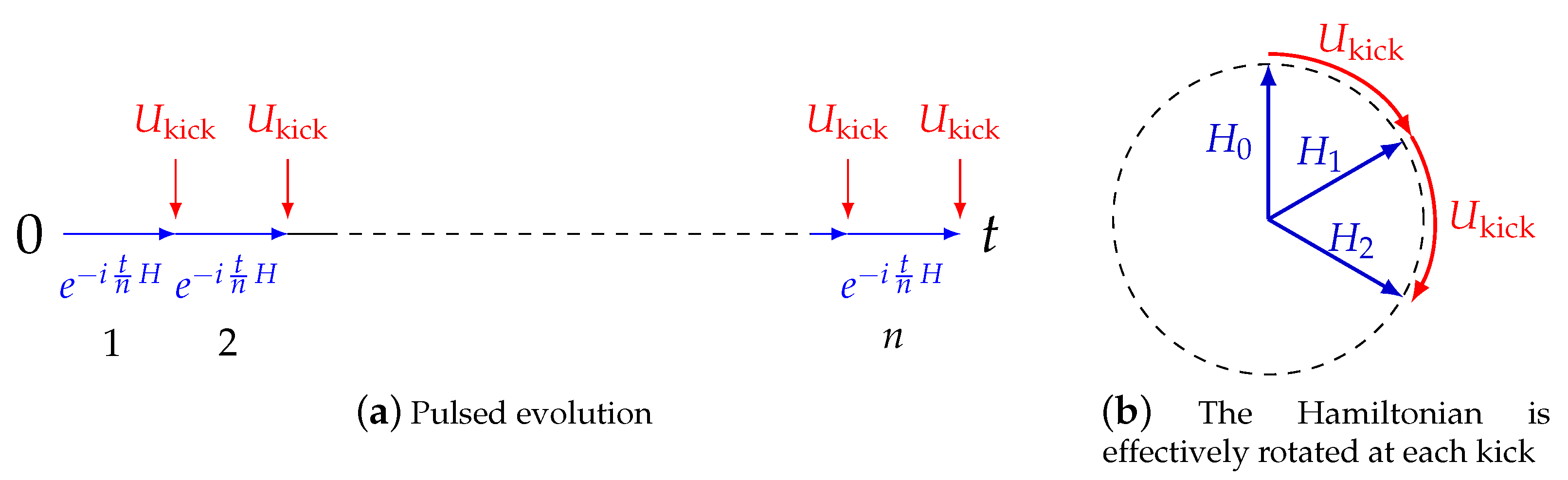
3. Pulsed Decoupling
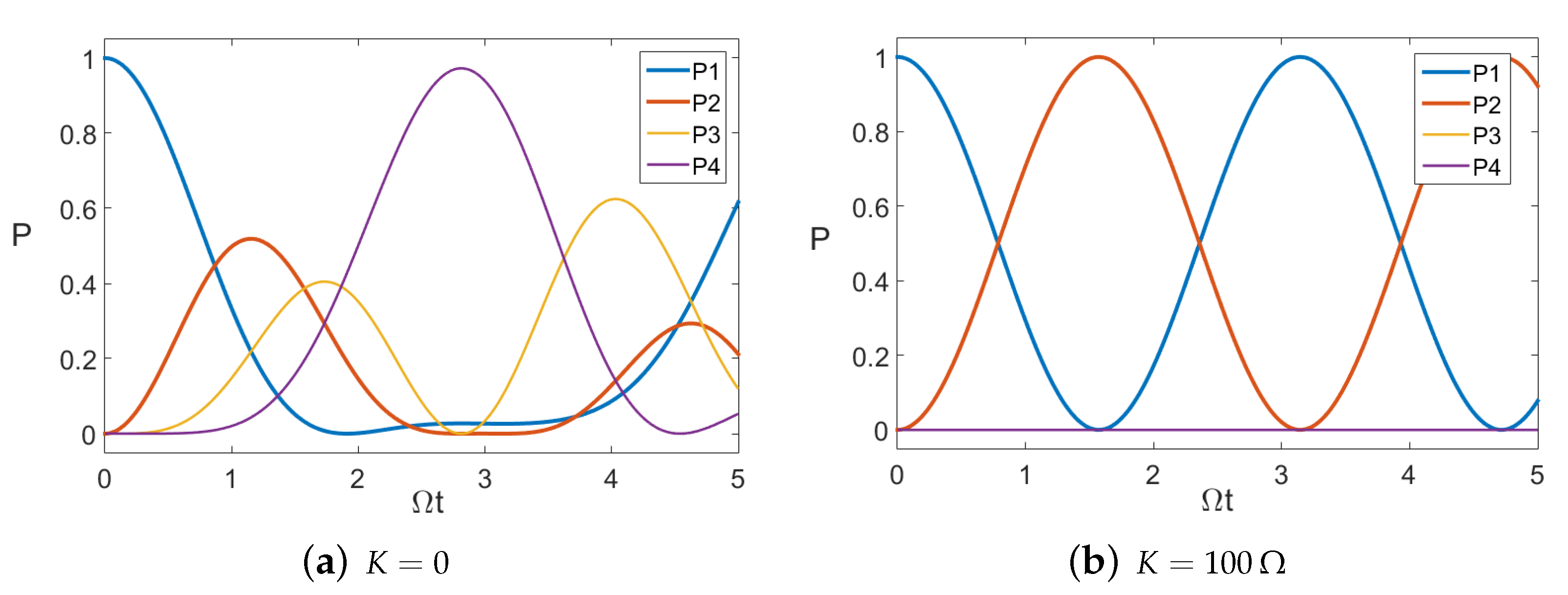
4. Example: Four-Level System
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Misra, B.; Sudarshan, E.G. The Zeno’s paradox in quantum theory. J. Math. Phys. 1977, 18, 756–763. [Google Scholar] [CrossRef]
- Facchi, P.; Pascazio, S. Quantum Zeno Subspaces. Phys. Rev. Lett. 2002, 89, 080401. [Google Scholar] [CrossRef]
- Burgarth, D.; Facchi, P.; Gramegna, G.; Pascazio, S. Generalized Product Formulas and Quantum Control. arXiv 2019, arXiv:1906.04498. [Google Scholar] [CrossRef]
- Facchi, P. Quantum Zeno effect, adiabaticity and dynamical superselection rules. In Fundamental Aspects of Quantum Physics, Proceedings of the Quantum Probability and White Noise Analysis XVII, Tokyo, Japan, 27–29 September 2001; World Scientific: Hackensack, NJ, USA, 2001; Volume 197. [Google Scholar] [CrossRef]
- Kato, T. On the Adiabatic Theorem of Quantum Mechanics. J. Phys. Soc. Japan 1950, 5, 435–439. [Google Scholar] [CrossRef]
- Facchi, P.; Lidar, D.; Pascazio, S. Unification of Dynamical Decoupling and the Quantum Zeno Effect. Phys. Rev. A 2004, 69, 032314. [Google Scholar] [CrossRef]
- Schäfer, F.; Herrera, I.; Cherukattil, S.; Lovecchio, C.; Cataliotti, F.S.; Caruso, F.; Smerzi, A. Experimental realization of quantum Zeno dynamics. Nat. Comm. 2014, 5, 3194. [Google Scholar] [CrossRef] [PubMed]
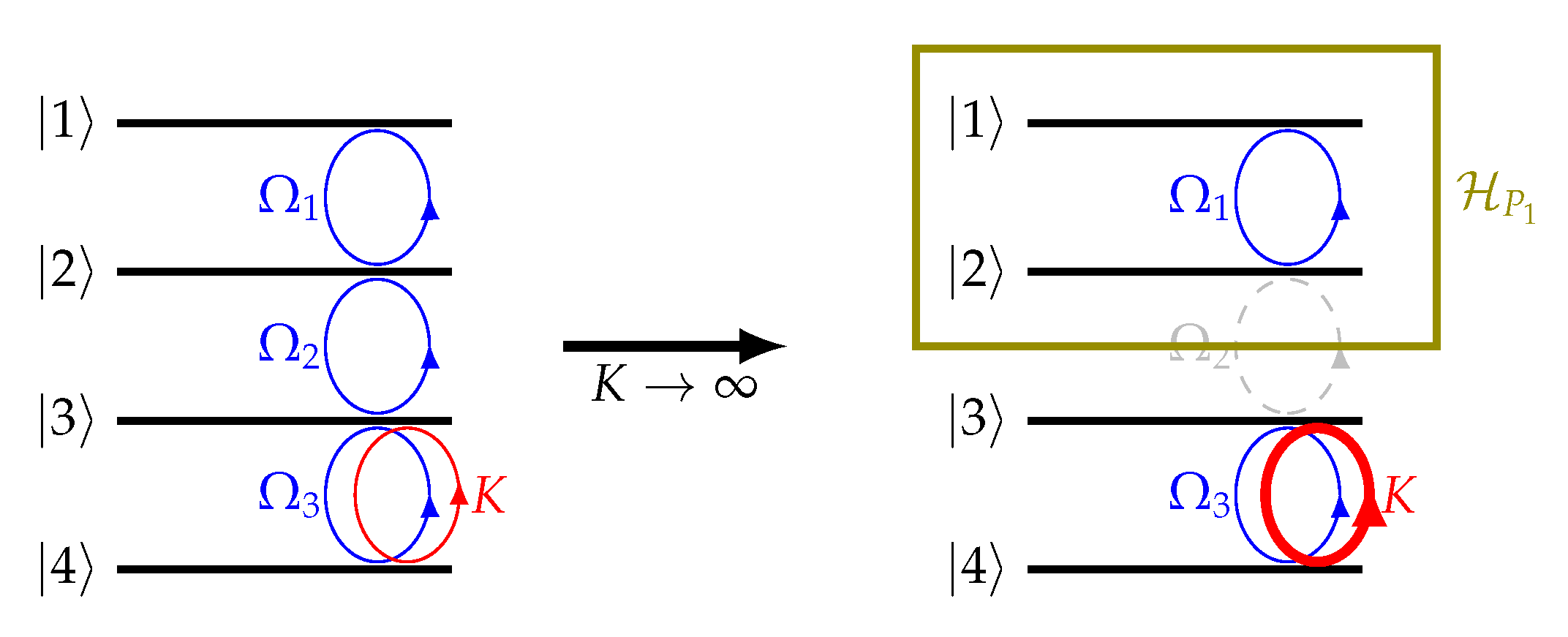
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gramegna, G.; Burgarth, D.; Facchi, P.; Pascazio, S. Continuous and Pulsed Quantum Control. Proceedings 2019, 12, 15. https://doi.org/10.3390/proceedings2019012015
Gramegna G, Burgarth D, Facchi P, Pascazio S. Continuous and Pulsed Quantum Control. Proceedings. 2019; 12(1):15. https://doi.org/10.3390/proceedings2019012015
Chicago/Turabian StyleGramegna, Giovanni, Daniel Burgarth, Paolo Facchi, and Saverio Pascazio. 2019. "Continuous and Pulsed Quantum Control" Proceedings 12, no. 1: 15. https://doi.org/10.3390/proceedings2019012015
APA StyleGramegna, G., Burgarth, D., Facchi, P., & Pascazio, S. (2019). Continuous and Pulsed Quantum Control. Proceedings, 12(1), 15. https://doi.org/10.3390/proceedings2019012015




