Privacy in Quantum Estimation ^†

Abstract

We introduce the notion of privacy in quantum estimation by considering an one-parameter family of isometries taking one input into two output systems. It stems on the separate and adversarial control of the two output systems as well as on the local minimization of the mean square error. Applications to two-qubit unitaries (with one qubit in a fixed input state) are presented.

1. Introduction

Parameter estimation is becoming important in quantum information processing which takes place by quantum channel maps (see e.g., [1]). It is well known that any quantum channel admits an isometry as a dilation [2]. Hence we can conceive the estimation of a family of isometries through quantum channels. This models a realistic situation where not all information concerning the measured systems is accessible. More precisely, given a one parameter family of isometries $\left\{V_{\alpha }^{A\to BF}\right\}$, we consider the parameter $\alpha$’s estimation by accessing only the system B. This amounts to use the quantum channel between A and B of which $V_{\alpha }^{A\to BF}$ represents the Stinespring dilation [2].

In communication theory channels are also characterized by their privacy [3]. This notion captures the ability to convey more information through the channel than the one that is lost into environment. To link this notion with estimation we assume system F is under control of a malicious being. Then the problem we are facing with becomes of what are the conditions under which a legitimate user controlling the B system (besides A ones) can perform a better estimation. We address this issue by minimizing mean square error.

2. Private Quantum Estimation

Consider a family of isometries $V_{\alpha }:{\mathcal{H}}_A\to {\mathcal{H}}_B\otimes {\mathcal{H}}_F,$ which is parametrized by $\alpha \in \mathcal{I}\subset \mathbb{R}$. Assume parameter $\alpha$ has an a priori probability distribution function $p\left(\alpha \right)$ over $\mathcal{I}$, the probe system A is prepared in the state ${\rho }_A$. Then the output on B reads

$${\rho }_B\left(\alpha \right)={\mathrm{Tr}}_F\left(V_{\alpha }{\rho }_A{V}_{\alpha }^{†}\right)=:\mathcal{N}\left({\rho }_A\right).$$

(1)

We perform measurement on this state, and estimate of the unknown parameter $\alpha$ using the measurement outcome. As goodness of this process, we consider average quadratic cost function:

$${\overline{C}}^B:={\int }_{\mathcal{I}}p\left(\alpha \right)\mathrm{Tr}\left[{\rho }_B\left(\alpha \right){\left({\widehat{S}}_B-\alpha I\right)}^2\right]d\alpha ,$$

(2)

where ${\widehat{S}}_B$ is the measurement operator used to estimate $\alpha$. The best of such operator is obtained by minimizing ${\overline{C}}^B$. Personik’s theorem [4] provided the solution to this optimization problem through the following operator equation

$$W_B^{\left(0\right)}{\widehat{S}}_B+{\widehat{S}}_B{W}_B^{\left(0\right)}=2W_B^{\left(1\right)},$$

(3)

where $W_B^{\left(0\right)}:={\int }_{\mathcal{I}}p\left(\alpha \right){\rho }_B\left(\alpha \right)d\alpha$ and $W_B^{\left(1\right)}:={\int }_{\mathcal{I}}\alpha p\left(\alpha \right){\rho }_B\left(\alpha \right)d\alpha .$ On the other hand we can consider the state emerging from the channel complementary to $\mathcal{N}$ in Equation (1), namely

$${\rho }_F\left(\alpha \right)={\mathrm{Tr}}_B\left(V_{\alpha }{\rho }_A{V}_{\alpha }^{†}\right)=:\tilde{\mathcal{N}}\left(\rho \right).$$

(4)

If this is controlled by an adversary, a strategy similar to the above can be employed to estimate $\alpha$ and leading to ${\overline{C}}_{min}^F$ with a suitable optimal measurement ${\widehat{S}}_F$.

By considering the system B (as well as A) hold by a legitimate user, we define the privacy of estimation through the difference between the minimum of the average quadratic cost functions

$${\mathcal{P}}_e:=max\left\{{\overline{C}}_{min}^F-{\overline{C}}_{min}^B,0\right\}.$$

(5)

Whenever it results positive, it means that ${\overline{C}}_{min}^B<{\overline{C}}_{min}^F$ and hence B can better estimate $\alpha$ than F. This definition of the privacy assumes that the adversary can control the system F and at the same time has information about the input state. A weaker notion of privacy can be introduced by assuming the adversary with no information about the input state. This amounts to consider ${\overline{C}}_{min}^F$ in (5) averaged overall possible input states.

3. Application to Two-Qubit Unitaries

For a two-qubit system we consider $V_{\alpha }=U_{\alpha }{|0\rangle }_E$, where $U_{\alpha }:{\mathcal{H}}_A\otimes {\mathcal{H}}_E\to {\mathcal{H}}_B\otimes {\mathcal{H}}_F$ (${\mathcal{H}}_A={\mathcal{H}}_E={\mathcal{H}}_B={\mathcal{H}}_F\simeq {\mathbb{C}}^2$) are entangling unitaries that can be parameterized as [5]:

$$U({\alpha }_x,{\alpha }_y,{\alpha }_z)=exp\left[-\frac{i}{2}\left({\alpha }_x{\sigma }_x\otimes {\sigma }_x+{\alpha }_y{\sigma }_y\otimes {\sigma }_y+{\alpha }_z{\sigma }_z\otimes {\sigma }_z\right)\right],$$

(6)

with the parameter space

$$\mathcal{S}=\left\{({\alpha }_x,{\alpha }_y,{\alpha }_z):\frac{\pi }{2}\ge {\alpha }_x\ge {\alpha }_y\ge {\alpha }_z\ge 0\right\}.$$

(7)

The state in the system A (probe’s state) will be generically considered as

$${\rho }_A=\left(\sqrt{x}|0\rangle +e^{i\phi }\sqrt{1-x}|1\rangle \right)\left(\sqrt{x}\langle 0|+e^{-i\phi }\sqrt{1-x}\langle 1|\right),$$

(8)

with $x\in [0,1]$ and $\phi \in [0,2\pi ]$. Below we will consider the estimation of a single parameter be either ${\alpha }_x$ or ${\alpha }_y$ or ${\alpha }_z$, by assuming the values of the other two to be known. To this end the states ${\rho }_B$ of Equation (1) and ${\rho }_F$ of Equation (4) can be readily calculated. There, the parameter $\phi$ appears as added to ${\alpha }_z$. Thus it has no effect in the estimation of the latter. But it can affect the estimation of ${\alpha }_x$ and ${\alpha }_y$.

(i)

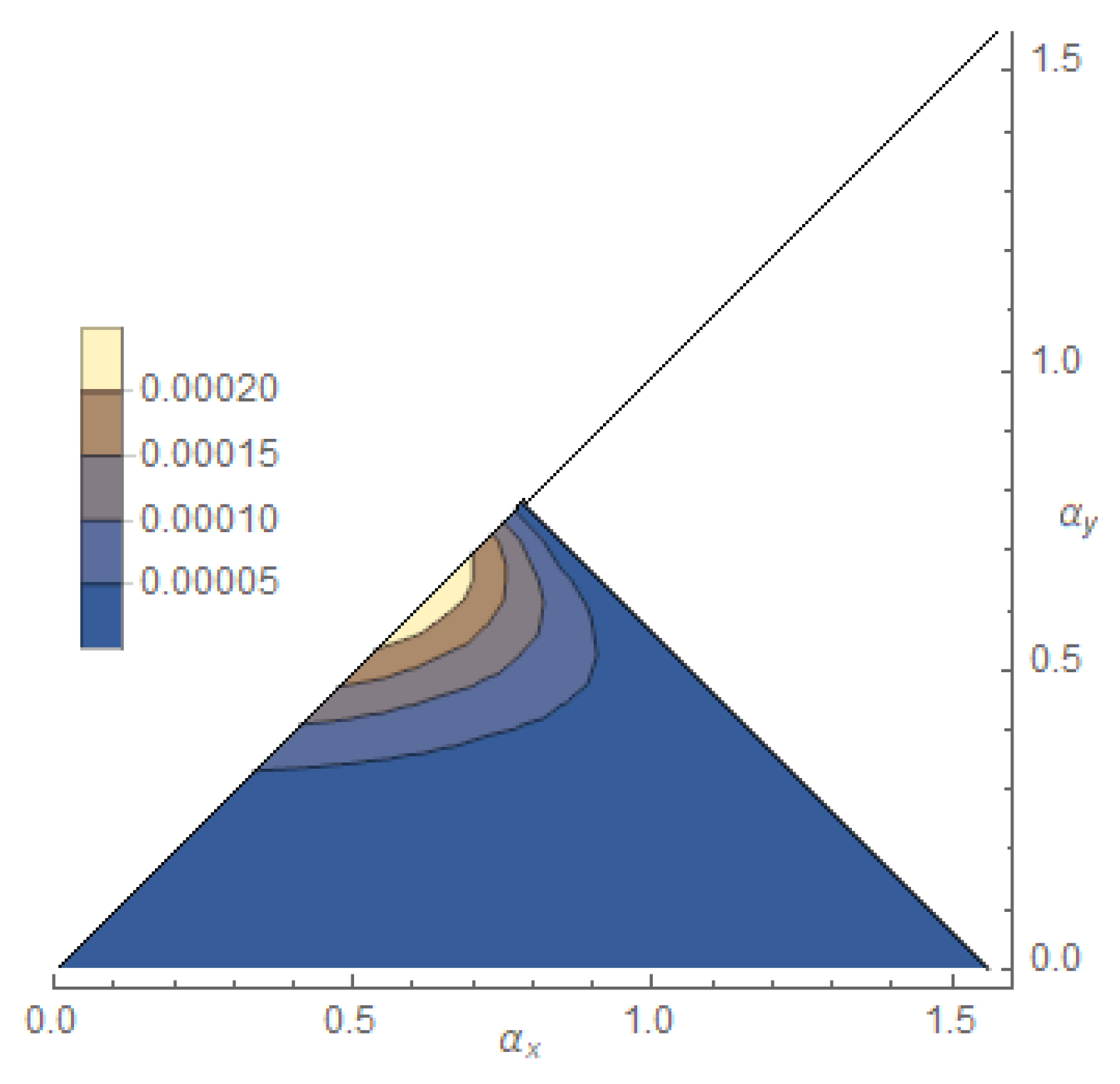
Estimation of ${\alpha }_z$. We took 325 points in the region $0\le {\alpha }_y\le {\alpha }_x\le \frac{\pi }{2}$ and for each point we estimated ${\alpha }_z$ through ${\rho }_B$ and independently through ${\rho }_F$. This is done by also optimizing the privacy (5) over the probe’s state, i.e., by considering

$${\mathcal{P}}_e({\alpha }_x,{\alpha }_y)=max\left\{\underset{x}{max}\left[{\overline{C}}_{min}^F({\alpha }_x,{\alpha }_y,x)-{\overline{C}}_{min}^B({\alpha }_x,{\alpha }_y,x)\right],0\right\},$$

(9)

whose contour plot is reported in Figure 1.

On the line ${\alpha }_x+{\alpha }_y=\frac{\pi }{2}$ we have ${\overline{C}}_{min}^B={\overline{C}}_{min}^F$ and this divides the region $0\le {\alpha }_y\le {\alpha }_x\le \frac{\pi }{2}$ into two triangles. Only in the lower one the estimation is private (in the upper one ${\overline{C}}_{min}^F$ results smaller than ${\overline{C}}_{min}^B$). Furthermore there is a specific and small region where the privacy increases with respect to the background.

(ii)

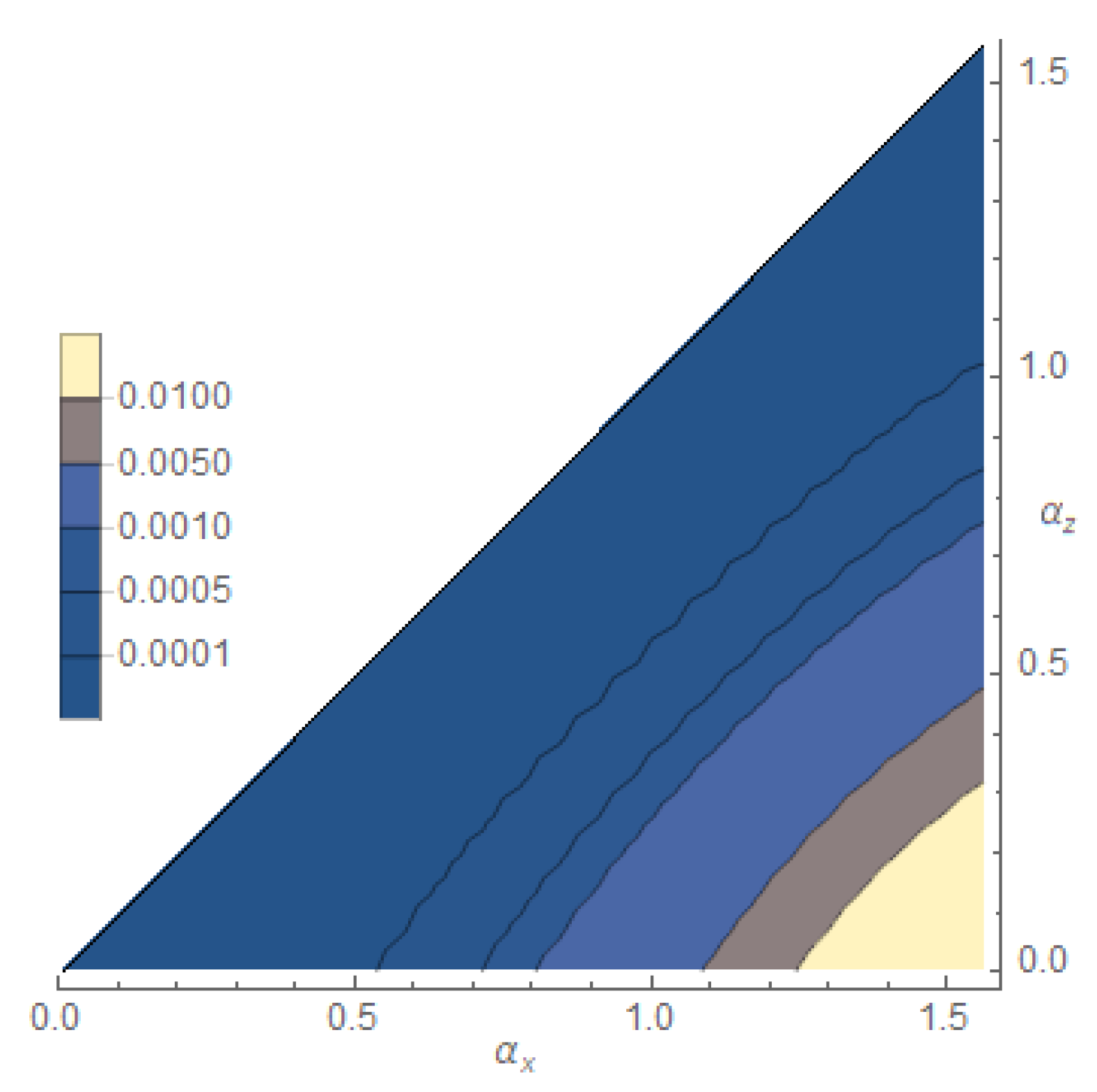
Estimation of ${\alpha }_y$. In this case we took 325 points in the region $0\le {\alpha }_z\le {\alpha }_x\le \frac{\pi }{2}$, and for each point we estimated ${\alpha }_y$ through ${\rho }_B$ and independently through ${\rho }_F$ likewise the previous case. Then we evaluated the privacy

$${\mathcal{P}}_e({\alpha }_x,{\alpha }_z)=max\left\{\underset{x,\phi }{max}\left[{\overline{C}}_{min}^F({\alpha }_x,{\alpha }_z,x,\phi )-{\overline{C}}_{min}^B({\alpha }_x,{\alpha }_z,x,\phi )\right],0\right\},$$

(10)

whose contour plot is reported in Figure 2. Notice that although ${\overline{C}}_{min}^B$ can be made zero by choosing ${\alpha }_z={\alpha }_x$1, this does not give the maximum privacy since in such a case also ${\overline{C}}_{min}^F$ turns out to be zero. The maximum privacy is obtained when ${\alpha }_z$ decrease to 0 and ${\alpha }_x$ increase to $\pi /2$.

(iii)

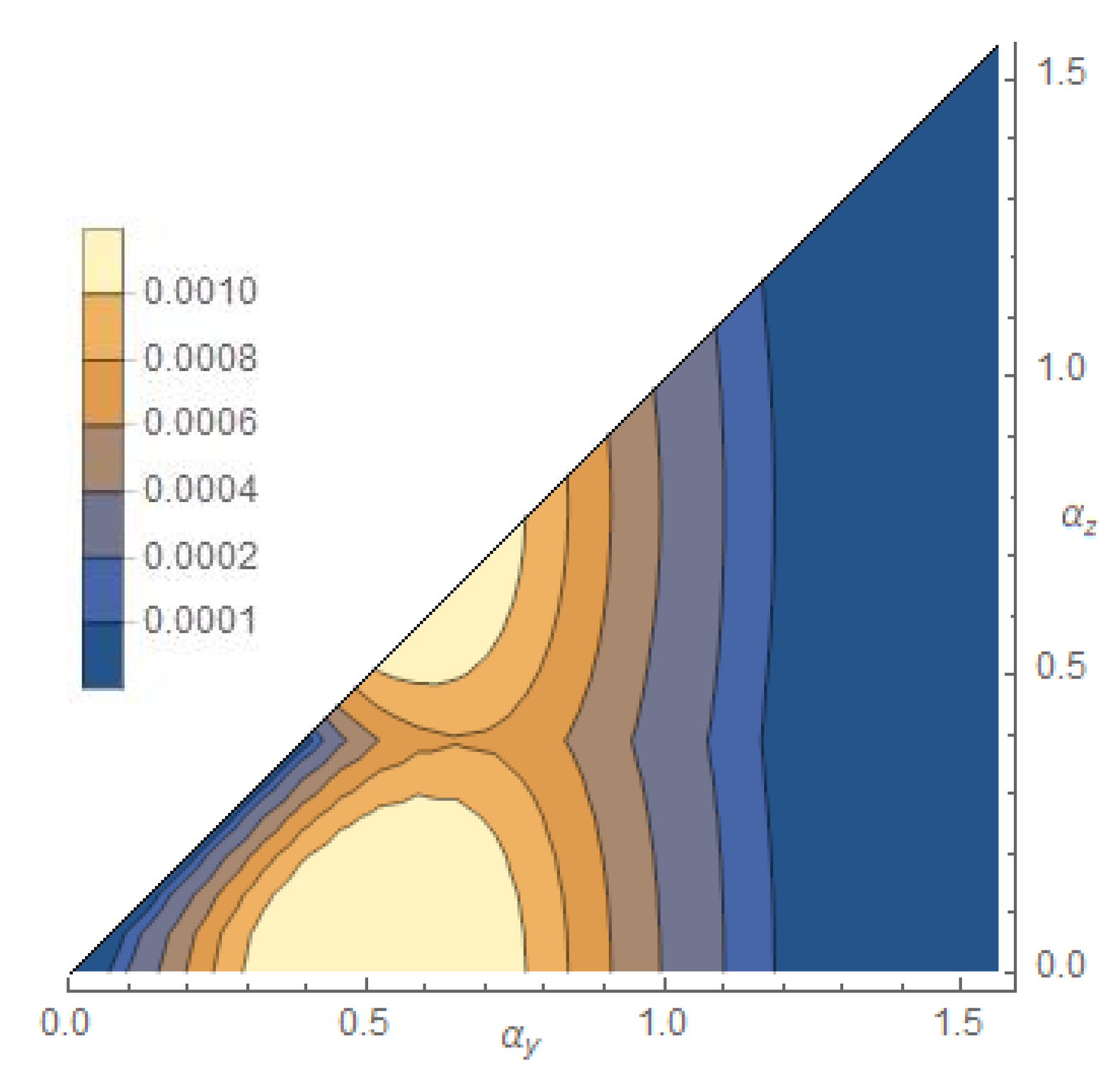
Estimation of ${\alpha }_x$. In this last case we took 325 points in the region $0\le {\alpha }_z\le {\alpha }_y\le \frac{\pi }{2}$ and for each point we estimated ${\alpha }_x$ through ${\rho }_B$ and independently through ${\rho }_F$. We actually computed

$${\mathcal{P}}_e({\alpha }_y,{\alpha }_z)=max\left\{\underset{x,\phi }{max}\left[{\overline{C}}_{min}^F({\alpha }_y,{\alpha }_z,x,\phi )-{\overline{C}}_{min}^B({\alpha }_y,{\alpha }_z,x,\phi )\right],0\right\},$$

(11)

whose contour plot is shown in Figure 3.

Comparing the three cases we can see that the highest privacy is achievable for the estimation of ${\alpha }_y$, while it decreases by one order of magnitude for ${\alpha }_x$ and by a further order of magnitude for ${\alpha }_z$. In this latter case the privacy is also not guaranteed in half of the parameter space. It is worth saying that ${\mathcal{P}}_e({\alpha }_x,{\alpha }_y)$ is not affected by the maximization over $\phi$, while the quantities ${\mathcal{P}}_e({\alpha }_x,{\alpha }_z)$ and ${\mathcal{P}}_e({\alpha }_y,{\alpha }_z)$ are, but in a different way. In particular the former is almost insensible to $\phi$, instead the latter strongly depends on it.

4. Conclusion

In conclusion we have considered the single parameter estimation of isometries representing Stinespring dilations of quantum channels, in which the environment is under control of an adversary and the goal is to allow the legitimate user of the channels to outperform the estimation. The optimal strategy has been found by minimizing the average quadratic cost. Applications to two-qubit unitaries show that the largest privacy is obtainable when estimating ${\alpha }_y$, i.e., the parameter in front of the generator ${\sigma }_y\otimes {\sigma }_y$. The developed approach can be extended to conceive the possibility of separate but cooperative control (instead of adversarial) of the two output systems [6].