Heavy Hadrons Production by Coalescence Plus Fragmentation in AA Collisions at RHIC and LHC ^†

Abstract

The hadronization process of heavy hadrons with bottom and charm quarks, especially for baryons ${\mathsf{\Lambda }}_c$, in a dense QGP medium is largely not understood. We present within a coalescence plus fragmentation model the predictions for $D^0$ and ${\mathsf{\Lambda }}_c$ spectra and the related baryon to meson ratios at RHIC and LHC. We will discuss how our model can predict values for ${\mathsf{\Lambda }}_c$/$D^0$ of the order of O(1), which is much larger than the expectations from fragmentation, and in agreement whit early data from STAR collaboration. Furthermore in the same scheme can be predicted a baryon to meson ratio ${\mathsf{\Lambda }}_c$/$D^0$ in pp collisions assuming that at the LHC top energies there can be the formation of QGP matter. The results show a considerable volume effects that significantly reduce the ratios, but still predict quite larger values with respect to fragmentation, in agreement with recent data from ALICE in pp collisions.

1. Introduction

Ultra-relativistic heavy ion collision at Large Hadron Collider (LHC) and at Relativistic Heavy-Ion Collider (RHIC) have been designed to reach a new state of matter composed of a strongly interacting plasma of deconfined quark and gluons the so called Quark-Gluon Plasma (QGP). The bulk properties of the matter created are governed by the light quarks and gluons while heavy quarks like charm or bottom quarks are useful probes of the QGP properties [1,2,3,4,5,6,7,8,9,10,11,12]. In their final state the charm quarks appear as constituent of charmed hadrons mainly D mesons and ${\mathsf{\Lambda }}_c$, ${\mathsf{\Sigma }}_c$ baryons. Recent experimental results from STAR collaboration have shown an enhancement of the baryon/meson ratio in the heavy flavor sector like the one observed for light and strange hadrons compared to the one for p-p collision [13,14,15]. In particular the experimental data in 10%–60% central $Au+Au$ collisions have shown a ${\mathsf{\Lambda }}_c/D^0\sim 0.8÷1.5$ for $3<p_T<6GeV$ which is a very large enhancement compared to the value predicted by the charm hadron fragmentation ratio for p+p collisions [16]. The idea of the coalescence model comes from the fact that comoving partons in the QGP combine their transverse momentum to produce a final-state meson or baryon with higher transverse momentum [17,18,19,20]. Few studies have investigated the modification of the relative abundance of the different heavy hadron species produced. In particular this can manifests in a baryon-to-meson enhancement for charmed hadrons [21,22].

2. Coalescence plus Fragmentation Model

The coalescence approach is based on the Wigner formalism, the momentum spectrum of hadrons formed by coalescence of quarks can be written as:

$$\frac{d^2{N}_H}{d{P}_T^2}=g_H\int \prod _{i=1}^n\frac{d^3{p}_i}{{\left(2\pi \right)}^3{E}_i}{p}_i·d{\sigma }_i{f}_{q_i}(x_i,p_i)f_H(x_1...x_n,p_1...p_n){\delta }^{\left(2\right)}\left(P_T-\sum _{i=1}^n{p}_{T,i}\right)$$

(1)

where $d{\sigma }_i$ denotes an element of a space-like hypersurface, $g_H$ is the statistical factor to form a colorless hadron while $f_{q_i}$ are the quark (anti-quark) phase-space distribution functions for i-th quark (anti-quark). $f_H(x_1...x_n,p_1...p_n)$ is the Wigner function and describes the spatial and momentum distribution of quarks in a hadron and can be related to the hadron wave function. The Wigner distribution function used has a Gaussian shape in space and momentum, $f_M(x_1,x_2;p_1,p_2)=A_{W}exp(-\frac{x_{r1}^2}{{\sigma }_r^2}-p_{r1}^2{\sigma }_r^2)$ where $x_{r1}$ and $p_{r1}$ are the 4-vectors for the relative coordinates. $A_W$ is a normalization constant fixed to guarantee that in the limit $p\to 0$ we have all the charm hadronizing. While ${\sigma }_r$ is the covariant width parameter and it can be related to the oscillator frequency $\omega$ by $\sigma =1/\sqrt{\mu \omega }$ where $\mu =\left(m_1{m}_2\right)/(m_1+m_2)$ is the reduced mass. The width of $f_M$ can be related to the size of the hadron and in particular to the root mean square charge radius of the meson. For $D^{+}$ meson ${⟨r^2⟩}_{ch}=0.184f{m}^2$ corresponding to a ${\sigma }_p={\sigma }_r^{-1}=0.283GeV$; for ${\mathsf{\Lambda }}_c^{+}$ the widths are fixed by the mean square charge radius of ${\mathsf{\Lambda }}_c^{+}$ which is given by ${⟨r^2⟩}_{ch}=0.15f{m}^2$.

We compute the coalescence probability $P_{coal}$ for each charm quark then we can assign a probability of fragmentation as $P_{frag}\left(p_T\right)=1-P_{coal}\left(p_T\right)$. Therefore the hadron momentum spectra from the charm spectrum $d{N}_{fragm}/d^2{p}_{T}dy$ that do not undergo to coalescence is given by the convolution with the fragmentation function,for D and ${\mathsf{\Lambda }}_c^{+}$ we employ the Peterson fragmentation function [23]$D_{had}(z,Q^2)\propto 1/\left[z{\left[1-\frac{1}{z}-\frac{{ϵ}_c}{1-z}\right]}^2\right]$, where ${ϵ}_c$ is a free parameter to fix the shape of the fragmentation function and is determined assuring that the experimental data on D and ${\mathsf{\Lambda }}_c$ production in $p+p$ collisions are well described by a fragmentation hadronization mechanism. The value it has been fixed to ${ϵ}_c=0.06$ and ${ϵ}_c=0.12$ as discussed in [5]. The relative ratios between different hadron channels are properly calculated and normalized according to the ratio of fragmentation fraction in [16].

2.1. Fireball parameters and quark distribution

We consider the systems created at RHIC in Au+Au collisions at $\sqrt{s_{NN}}=200$ GeV and at LHC in Pb+Pb collisions at $\sqrt{s_{NN}}=2.76TeV$. Our approach is based on a fireball where the bulk of particles is a thermalized system of gluons and $u,d,s$ quarks and anti-quarks. The fireball is considered at $\tau =7.8fm/c$, for LHC, and $\tau =4.5fm/c$, for RHIC, and the system has a temperature of $T_C=165\mathrm{MeV}$. To take into account for the collective flow, we assume a radial flow profile as ${\beta }_T\left(r_T\right)={\beta }_{max}\frac{r_T}{R}$, where R is the transverse radius of the fireball. For partons at low transverse momentum, $p_T<2GeV$, hence we consider a thermal distribution, instead for $p_T>2.5GeV$, we consider the minijets that have undergone the jet quenching mechanism. For heavy quarks we use the transverse momentum distribution obtained by solving the relativistic Boltzmann equation [5] giving a good description of $R_{AA}$ and $v_2$ of D mesons. The heavy quark numbers are estimated to be $d{N}_c/dy\simeq 2$ at RHIC and $d{N}_c/dy\simeq 15$ at LHC in agreement with the energy dependence of charm production cross section [24]. In the following calculation the charm quark mass used is $m_c=1.3GeV$.

3. Results

The coalescence probability is a decreasing function with $p_T$, and at low $p_T$ having a coalescence probability for ${\mathsf{\Lambda }}_c$ even larger than for $D^0$ is a quite peculiar feature of the coalescence mechanism that we expect to lead to large values of the ${\mathsf{\Lambda }}_c/D^0$ ratio [22].

In Figure 1a are shown the transverse momentum spectra at midrapidity for $Au+Au$ collisions at $\sqrt{s}=200\mathrm{GeV}$ and for (0%–10%) centrality for $D^0$ meson (left panel) and for ${\mathsf{\Lambda }}_c^{+}$ baryon (right panel) [25], we can see that for $D^0$ the contribution of both mechanism is about similar for $p_T<3\mathrm{GeV}$ and at higher $p_T$ the fragmentation becomes the dominant. For ${\mathsf{\Lambda }}_c^{+}$ and $D^0$ we have included the main hadronic channels that comes from $D^{*0}$, $D^{*+}$,${\mathsf{\Sigma }}_c^{*}\left(2520\right)$ and ${\mathsf{\Sigma }}_c\left(2455\right)$. The coalescence mechanism is the dominant mechanism for the ${\mathsf{\Lambda }}_c^{+}$ production for $p_T<7\mathrm{GeV}$ and it is mainly related to the fragmentation fraction from the analysis in Ref. [16], where this fraction is about the $6\%$ of the total produced heavy hadrons.

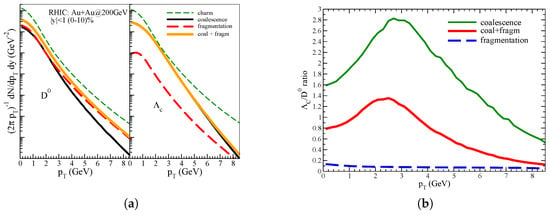
Figure 1. (Color online) (a) (left) Transverse momentum spectra at mid-rapidity for $Au+Au$ collisions at $\sqrt{s}=200\mathrm{GeV}$ and for (0%–10%) centrality for $D^0$ meson (left panel) and for ${\mathsf{\Lambda }}_c^{+}$ baryon (right panel). (b) (right) ${\mathsf{\Lambda }}_c^{+}$ to $D^0$ ratio as a function of $p_T$ and at mid-rapidity for $Au+Au$ collisions at $\sqrt{s}=200\mathrm{GeV}$ and for (10%–60%) centrality.

In Figure 1b we show the results for the ${\mathsf{\Lambda }}_c^{+}/D^0$ ratio. Coalescence by itself predicts a rise and fall of the baryon/meson ratio, the inclusion of fragmentation reduces the ratio, and we can see a quite good agreement with the experimental data in the peak region (orange solid line) in comparison with the STAR experimental data shown by circle [15,26]. In Figure 2a is shown the comparison between RHIC and LHC for the ${\mathsf{\Lambda }}_c^{+}/D^0$ ratio. Coalescence predicts a similar ratio for both energies, and the same for fragmentation, because the ratio established from the experimental measured fragmentation fraction remains the same changing the collision energy. Even if the only coalescence and the only fragmentation ratio remain similar, the combined ratio is different because, for each species, the production ratio between coalescence and fragmentation is smaller at LHC than at RHIC. Therefore, at LHC the larger contribution in particle production from fragmentation [22,27] leads to a final ratio that is smaller than at RHIC. A baryon over meson ratio that is so large at low momenta, can lead also to a smaller $D^0$$R_{AA}$ in this region. It is consequence of the charm quark number conservation and the dominance of D mesons in the total particle production, in $pp$ collisions.

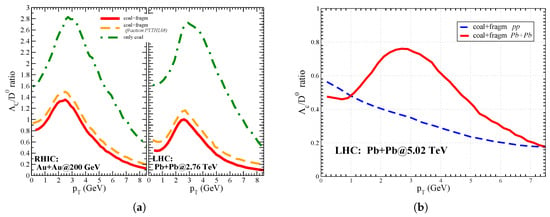
Figure 2. (Color online) (a) (left) ${\mathsf{\Lambda }}_c^{+}$ to $D^0$ ratio as a function of $p_T$ and at mid-rapidity for $Au+Au$ collisions at $\sqrt{s}=200\mathrm{GeV}$ (left panel) and for $Pb+Pb$ collisions at $\sqrt{s}=2.76\mathrm{TeV}$ (right panel). (b) (right) ${\mathsf{\Lambda }}_c^{+}$ to $D^0$ ratio as a function of $p_T$ and at mid-rapidity for $Pb+Pb$ collisions at $\sqrt{s}=5.02\mathrm{TeV}$

In recent years there has been a broadly discussed idea about the possible formation of QGP also in systems smaller than the one formed in heavy ion collision. We have applied our model in the case of $pp$ collisions, assuming that a medium is formed also in this small system like the one simulated in hydrodynamics calculations [28]. In Figure 2b is shown with the blue dashed line the ${\mathsf{\Lambda }}_c^{+}/D^0$ ratio obtained for this kind of system. Our calculations predict the disappearance of the peak, but an enhancement at low momenta that is significantly different from the ratio obtained with the only fragmentation. Moreover, the presence of a coalescence mechanism can have a deep impact on the $pp$ baseline used to evaluate the $R_{AA}$, in particular in the case of ${\mathsf{\Lambda }}_c$, where the presence of coalescence implies a different behavior especially at low momenta. This point is still completely open, because of the not yet available experimental data.