Abstract
We argue that the inferred ratio of shear viscosity to entropy density of the quark-gluon plasma, near the deconfinement temperature , can be understood from perturbative QCD. To rebut opposite views, we first show that the existing leading order result should not be expanded in logarithms. After then settling the question of scale for the running coupling, we establish a temperature dependence of which agrees well with constraints from hydrodynamics.
Experiments at the RHIC and LHC have provided substantial evidence that the quark-gluon plasma (QGP) behaves as an almost ideal fluid [1], with an upper bound on the ratio of shear viscosity to entropy density, . While this remarkably low value clearly indicates a ‘strongly coupled’ system, it remains a theoretical challenge to understand better why it is so low.
One popular approach to this question is via the AdS/CFT correspondence [2]. The conjectured lower limit from supersymmetric Yang-Mills theories does compare favorably with the observations, but a rigorous connection to real-world QCD is lacking. First attempts to compute by lattice QCD corroborate small values [3], but are hampered by the difficulties of applying a static approach for a non-equilibrium observables. On the other hand, there is a widespread belief that QCD perturbation theory fails to explain . This is the perception we will scrutinise here.
It appears to be largely based on the next-to-leading log (NLL) formula
where T is the temperature and the coupling strength. The coefficients b and c were extracted from the leading order (LO) result computed numerically in a QCD effective kinetic framework [4]. In the quenched limit ( quark flavors), the case we will consider mostly for argument’s sake, and . The viscosity should decrease for stronger interactions, which is described by (1) only for , at which point has a minimum. That minimum turns out to be close to the free entropy , see Figure 1. Thus (1) is incompatible with the bound .
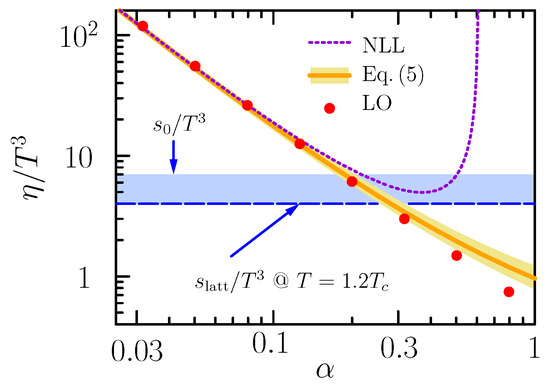
Figure 1.
The viscosity, for , to LO and NLL accuracy, and from our estimate (5). To illustrate that cannot explain (but may), we also show the constraint for the entropy, for (see main text). Near the deconfinement temperature the entropy of the QGP is notably smaller than .
We view the minimum of as a precursor to its singularity at (marking the break-down of the NLL approximation) – which an elementary argument reveals to be unphysical: In kinetic theory we may estimate , from the density n of particles that can transport a typical momentum over a distance . For binary interactions of relativistic particles , where is the transport cross section in terms of Mandelstam variables. (Here s is the centre-of-mass energy squared.) Although the ‘transport weight’ suppresses the influence of small-angle scatterings that prevail in gauge theories, would still diverge logarithmically at tree-level due to the t-channel gluon exchange term in . Since this would imply zero viscosity for any value of the coupling, it is a necessity to go beyond tree-level. In a hot QGP, the exchanged gluon acquires a self-energy of the order and is thus screened, schematically for small t. The typical invariant energy is much larger than for , thus screening can be mimicked by a cut-off on ,
This reproduces (with ) the parametric -dependence of (1), but also shows that the singularity of is related to coinciding integration bounds in (2). Thus the reason why cannot be extrapolated to larger has to do with kinematic simplifications that become illegitimate.
To validate this insight for QCD, the viscosity has to be calculated from the energy-momentum tensor of the particle distribution governed by the Boltzmann equation, , when set up for the case of a collective small-gradient flow u that drives f slightly out of local equilibrium. As detailed in Refs. [4,5], can be obtained by extremizing a functional constructed from the collision term . The essence of this technical calculation is [6]
if depends only on the Mandelstam variables, and omitting terms sub-leading to the dominant small-angle binary scattering contributions. With factorised from a positive weight , the convolution (3) specifies more rigorously the ‘typical’ momentum . We now discuss why the expansion in is ill-defined. To that end, we argue on the basis of (3) applied to the simple model which, now with correct kinematic limits, amends (2) to
Here is a monotonously decreasing, positive function of . Its ‘NLL’ approximation, , becomes obviously unphysical for , leading to the same issues as in (1) and (2). We note first that this problem cannot be cured by higher order terms in the expansion due to the convergence radius, , set by the pole at (off the physical sheet) in . This feature of a finite radius of convergence will carry over to QCD. What is more, expanding in before convoluting it in (3) with is forbidden: The coefficients of (the negative moments of P) are IR-divergent, with increasing severity, since [6].
Unless , estimates of cannot be based on the NLL formula (1) but require at least the unexpanded LO result. As a function of the coupling, is monotonously approaching zero, which begs the question for ‘the’ value of . To back up that perturbative QCD can indeed explain , let us point out that is fairly well reproduced by approximation (3) and (4). Without needing further details of we can simply rewrite the convolution in (3) using the mean value theorem,
Here we sidestepped solving the Boltzmann equation for f and infer that since (5) has to reproduce (1) at LL accuracy. Furthermore, could be determined from a ‘log moment’ of , but we will rather adjust it to match c in (1), viz. . To quantify the uncertainty of this artifice, we vary by factors in Figure 1, which confirms a good agreement of (5) with even for (where the NLL result becomes qualitatively incorrect, as discussed).
Figure 1 also depicts the rigorous bound on the entropy for known from lattice calculations [7], to affirm that cannot explain . For large enough could be compatible with – which brings us back to the task of specifying at a given T. A common prescription is to take as the running coupling
(where and is the QCD parameter) at a ‘typical thermal scale’, like the lowest Matsubara energy . However, quantifying the coupling should be based on firmer grounds.
Having to specify the coupling a posteriori arises because in Ref. [4] is treated as if it was constant. Imposing then as the relevant scale seems counterintuitive given the importance of a range of momenta, parametrically . As put forward early [8] but rarely taken into account in finite-T QCD, the relevant scale of the running coupling in, say, t-channel scattering should be . (Choosing a different scale gives correction terms which are higher order in but can be large.) This rectifies (2) to
hence the overall factor in (1) is to be understood as a geometric mean of the running coupling at and at the soft screening scale .
Running of the coupling emerges from fluctuations, be they in vacuum or in medium. Thus for observables that require thermal screening, the ‘scale setting’ for is unambiguous. For this, several types of radiative corrections are needed but only the gluon self-energy contributes in Coulomb gauge due to its Abelian-like Ward identities [9]. This noteworthy feature simplifies our argument. In Coulomb gauge it is evident that dressing e.g., a t-channel Born amplitude with (in dimensional regularization with scale L, and ) gives the renormalised with the coupling (6) at the scale t. At , the self-energy receives the finite contribution , where depends on and q. Then the renormalised amplitude becomes [10]. This dependence of the running coupling on the virtuality carries over to the other scattering channels and then to .
Now leaving behind the ‘toy’ models discussed, this analysis allows us to re-instate running in the fixed-coupling calculation [4], where IR sensitive terms in were screened with hard thermal loop (HTL) insertions, replacing e.g.,
Here , and is the Coulomb HTL propagator. The matrix element separates into transverse and longitudinal contributions (), with . Promoting to be -dependent gives the renormalised amplitude
The HTL screening in (7) and (8) is justified for soft momenta (which is sufficient for LO accuracy). To probe the sensitivity of higher order contributions, we omit screening for and then vary . Figure 2 shows a factor of two uncertainty of for relevant T, which makes our estimate based on the scale setting and omission of inelastic scatterings sufficiently robust [6].
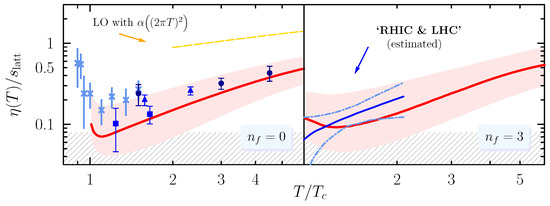
Figure 2.
The viscosity in units of the entropy [7]; full lines show our result with running coupling, the bands give the uncertainty from , see text. The left panel, for the quenched limit, shows lattice results [3], and by the dashed line the LO result with in running coupling. Overlayed on the right, for , are estimates from hydrodynamics [11]. Hatched region: .
In light of the overbearing sensitivity of on we set for the viscosity shown in Figure 2, normalised by the interacting entropy from lattice QCD calculations [7]. For our results are compatible with existing lattice calculations [3] and also recent constraints from hydrodynamics [11]. A mild increase in the ratio reflects the QCD feature of an effective coupling which weakens logarithmically. Figure 2 also illustrates that the LO result, with still overestimates .
We have demonstrated that many estimates for are misleading for two reasons, namely due to compromising the fixed- LO (resummed) result by another (log) expansion and an ad hoc choice for the value of . In fact, both issues are closely related: Resummation accounts for thermal screening which results from loop corrections to tree level amplitudes – as does running coupling. Treating them on an equal footing, we arrive at a consistent position regarding a long-standing question: The reckoned constraint for the QGP produced in heavy-ion collisions can be understood on the basis of the LO viscosity – rather than being a genuinely non-perturbative effect.
Acknowledgments
Greg Jackson was supported by the Swiss National Science Foundation (SNF) under grant 200020-168988.
References
- Aamodt, K.; Quintana, A.A.; Adamova, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agocs, A.G.; Agostinelli, A.; Salazar, S.A.; Ahammed, Z.; et al. Rapidity and transverse momentum dependence of inclusive J/ψ production in pp collisions at = 7 TeV. Phys. Lett. B 2011, 704, 442, Adare, A.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Al-Bataineh, H.; Alexander, J.; Al-Jamel, A.; Aoki, K.; Aphecetche, L.; et al. Heavy Quark Production in p + p and Energy Loss and Flow of Heavy Quarks in Au+Au Collisions at = 200 GeV. Phys. Rev. C 2011, 84, 044905. [Google Scholar] [CrossRef]
- Kovtun, P.; Son, D.T.; Starinets, A.O. Viscosity in strongly interacting quantum field theories from black hole physics. Phys. Rev. Lett. 2005, 94, 111601. [Google Scholar] [CrossRef]
- Meyer, H.B. A Calculation of the bulk viscosity in SU(3) gluodynamics. Phys. Rev. Lett. 2008, 100, 162001, Transport properties of the quark-gluon plasma from lattice QCD. Nucl. Phys. A 2009, 830, 641C; Mages, S.W.; Borsányi, S.; Fodor, Z.; Schäfer, A.; Szabó, K. Shear Viscosity from Lattice QCD. PoS LATTICE 2015, 2014, 232; Astrakhantsev, N.; Braguta, V.; Kotov, A. Temperature dependence of shear viscosity of SU(3)–gluodynamics within lattice simulation. JHEP 2017, 1704, 101. [Google Scholar] [CrossRef] [PubMed]
- Arnold, P.B.; Moore, G.D.; Yaffe, L.G. Transport coefficients in high temperature gauge theories. 1. Leading log results. JHEP 2000, 0011, 001, Transport coefficients in high temperature gauge theories. 2. Beyond leading log. ibid. 2003, 0305, 051. [Google Scholar] [CrossRef]
- Baym, G.; Monien, H.; Pethick, C.; Ravenhall, D. Transverse Interactions and Transport in Relativistic Quark-Gluon and Electromagnetic Plasmas. Phys. Rev. Lett. 1990, 64, 1867. [Google Scholar] [CrossRef] [PubMed]
- Jackson, G.; Peshier, A. Re-running the QCD shear viscosity. J. Phys. G 2018, 45, 095001. [Google Scholar] [CrossRef]
- Borsanyi, S.; Endrodi, G.; Fodor, Z.; Katz, S.D.; Szabo, K.K. Precision SU(3) lattice thermodynamics for a large temperature range. JHEP 2012, 1207, 056, Full result for the QCD equation of state with 2+1 flavors. Phys. Lett. B 2014, 730, 99. [Google Scholar] [CrossRef]
- Cutler, R.; Sivers, D.W. Quantum Chromodynamic Gluon Contributions to Large-pT Reactions. Phys. Rev. D 1978, 17, 196. [Google Scholar] [CrossRef]
- Grozin, A. Asymptotic freedom: History and interpretation. arXiv 2008, arXiv:0803.2589. [Google Scholar]
- Peshier, A. The QCD collisional energy loss revised. Phys. Rev. Lett. 2006, 97, 212301. [Google Scholar] [CrossRef] [PubMed]
- Bernhard, J.E.; Moreland, J.S.; Bass, S.A.; Liu, J.; Heinz, U. Applying Bayesian parameter estimation to relativistic heavy-ion collisions: Simultaneous characterization of the initial state and quark-gluon plasma medium. Phys. Rev. C 2016, 94, 024907. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).