1. Introduction
Heavy quarks are an important tool for the investigation of the quark-gluon plasma (QGP). They are primarily produced in the primordial hard collisions of the heavy ion collision, and their number is conserved until the hadronic freezout. Therefore heavy quarks carry information about the whole evolution of the QGP. Especially the surviving probability of heavy-quark bound states such as or can give an insight to the medium properties.
The potential between two heavy quarks is screened by the surrounding medium. As suggested long ago, the suppression of
could be an evidence for the formation of the deconfined state [
1]. Higher temperatures should lead to larger screening effects with a full suppression of
at very high beam energies. The predicted suppression was found at the SPS at CERN [
2] but measurements at RHIC at higher beam energies did not show an increase of the suppression [
3]. To explain the results the process of recombination of
inside the medium has been suggested. The theoretical investigation of recombination processes is therefore necessary to predict the number of
-mesons measured in the experiments.
The comparatively large masses of heavy quarks makes their motion accessible by Langevin dynamics [
4]. The forces that act on the charm quarks by using the Langevin equation are a drag force and random momentum kicks due to collisions with the medium particles. To enable the formation of bound states we add a potential between the heavy quarks.
2. Formalism
For the realization of the heavy-quark motion we adopt the formalism by Blaizot et al. [
5]. In this description the heavy-quark interaction is reduced to an Abelian model, which means that confinement and color effects are neglected. The Langevin update rules for the coordinate
and the momentum
of a heavy quark with mass
M read
where
is the friction coefficient due to the interaction with the medium,
is the force resulting from the heavy-quark potential,
T is the temperature of the medium, and
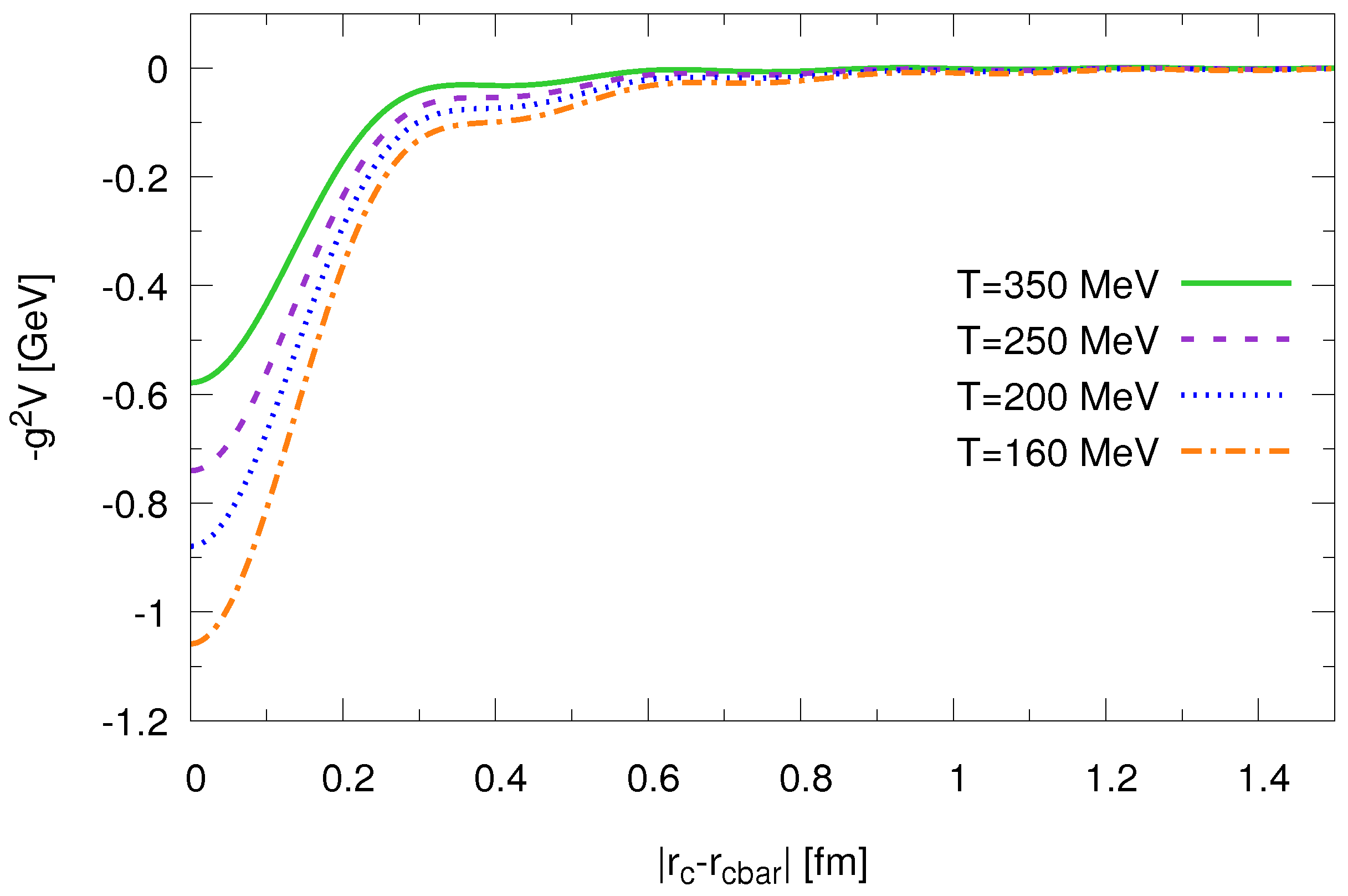
are Gaussian normal-distributed random numbers. For the pertinent diffusion coefficient the usual Einstein dissipation-fluctuation relation has been employed. The quark-anti-quark potential is given by a screened Coulomb potential with a cut-off for large momenta at small distances. Following [
5] the cut-off is taken to be
GeV. The potential for different temperatures is displayed in
Figure 1.
The drag force in [
5] contains a dependence on the distance between the heavy quarks. For simplicity we neglect this dependence in our simulation and use a constant drag coefficient. In a numerical calculation a cut-off is also necessary for the friction. With the same cut-off as for the potential the drag coefficient is given by
where
is the Debye screening mass, defined as
, which is the perturbative expression for a two-flavor quark-gluon plasma. The gauge coupling
g is given by the relation [
6]
where
is the critical temperature. The value of
at different temperatures can be seen in
Figure 2. The charm-quark mass is set to
.
3. Results and Discussion
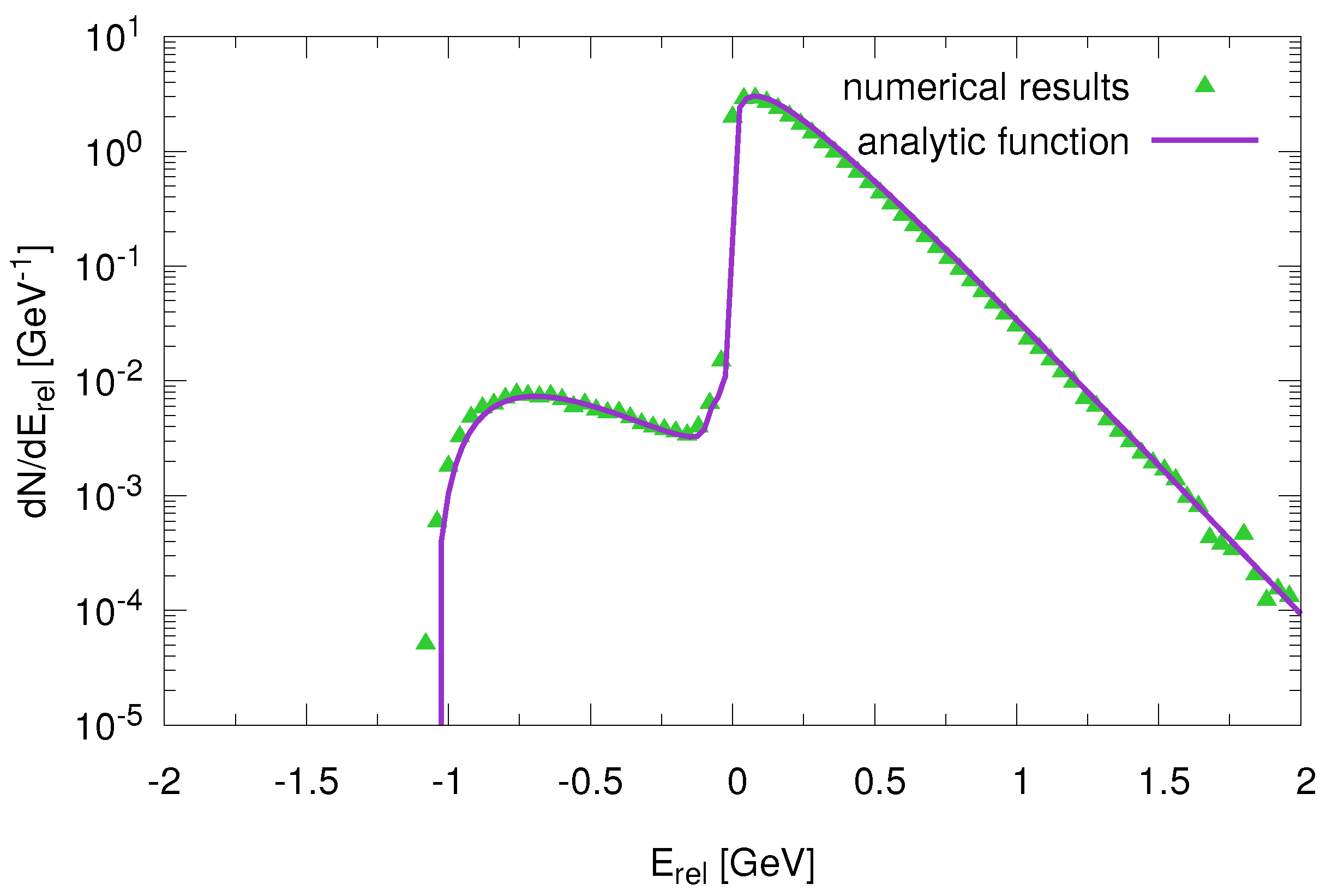
First the simulation was tested with a single charm-anticharm pair in the medium. The following simulations are done inside a cubic box with side-length 8 fm. To define bound states we use the classical condition that two objects are bound if the energy of the pair is negative. We calculate the relative energy
of the pair, which means subtracting the center-of-mass energy from the total energy. After the system reaches equilibrium the distribution of the relative energy should be given by the classical density of states
where
is the Hamiltonian of the pair and
C is a normalization constant. The results are shown in
Figure 3. For this plot both curves are normalized to one. We see that the numerical calculation perfectly fits to the analytic function.
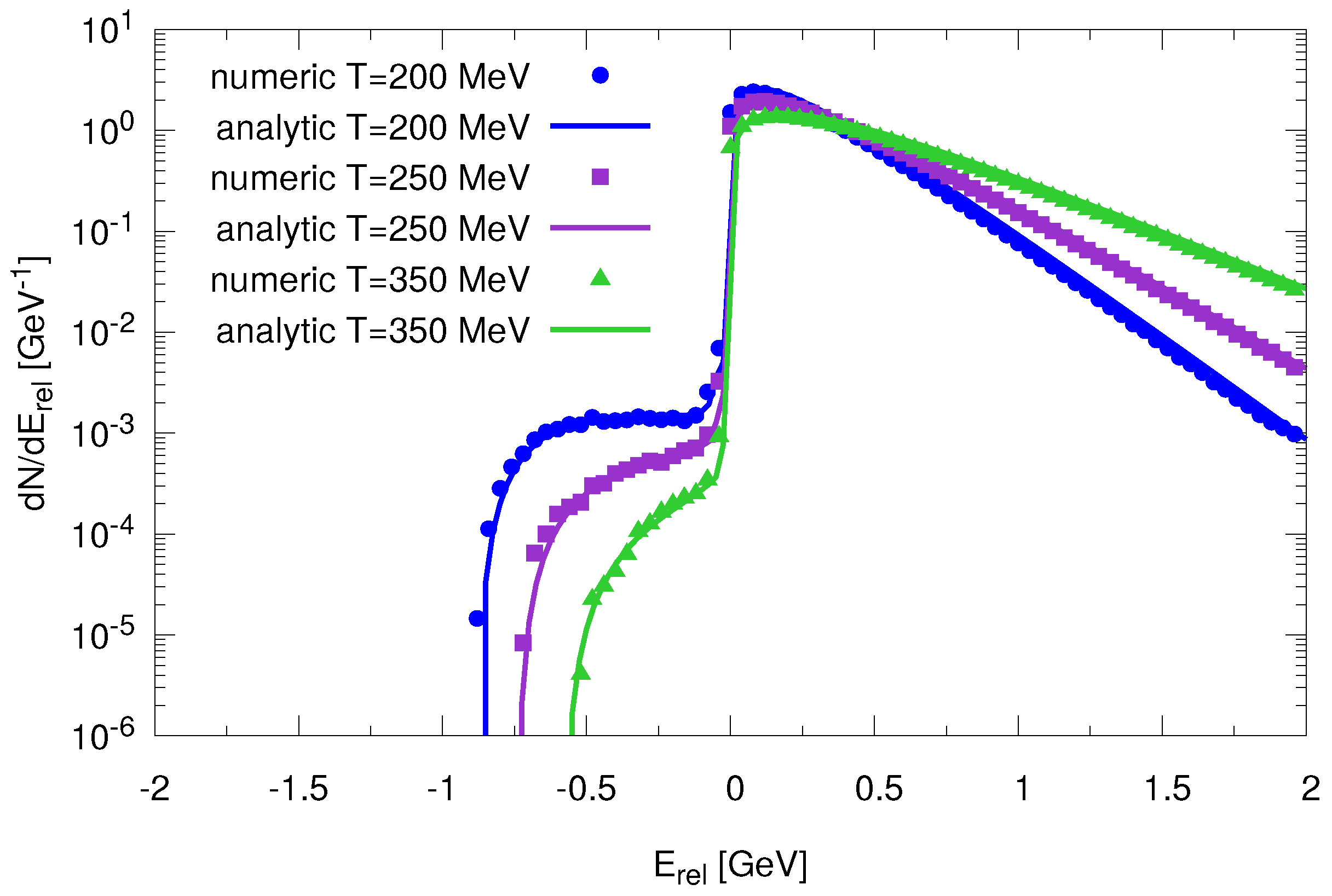
We also found this agreement for different temperatures, as can be seen in
Figure 4. For higher temperatures the number of bound states in equilibrium decreases due to stronger screening effects.
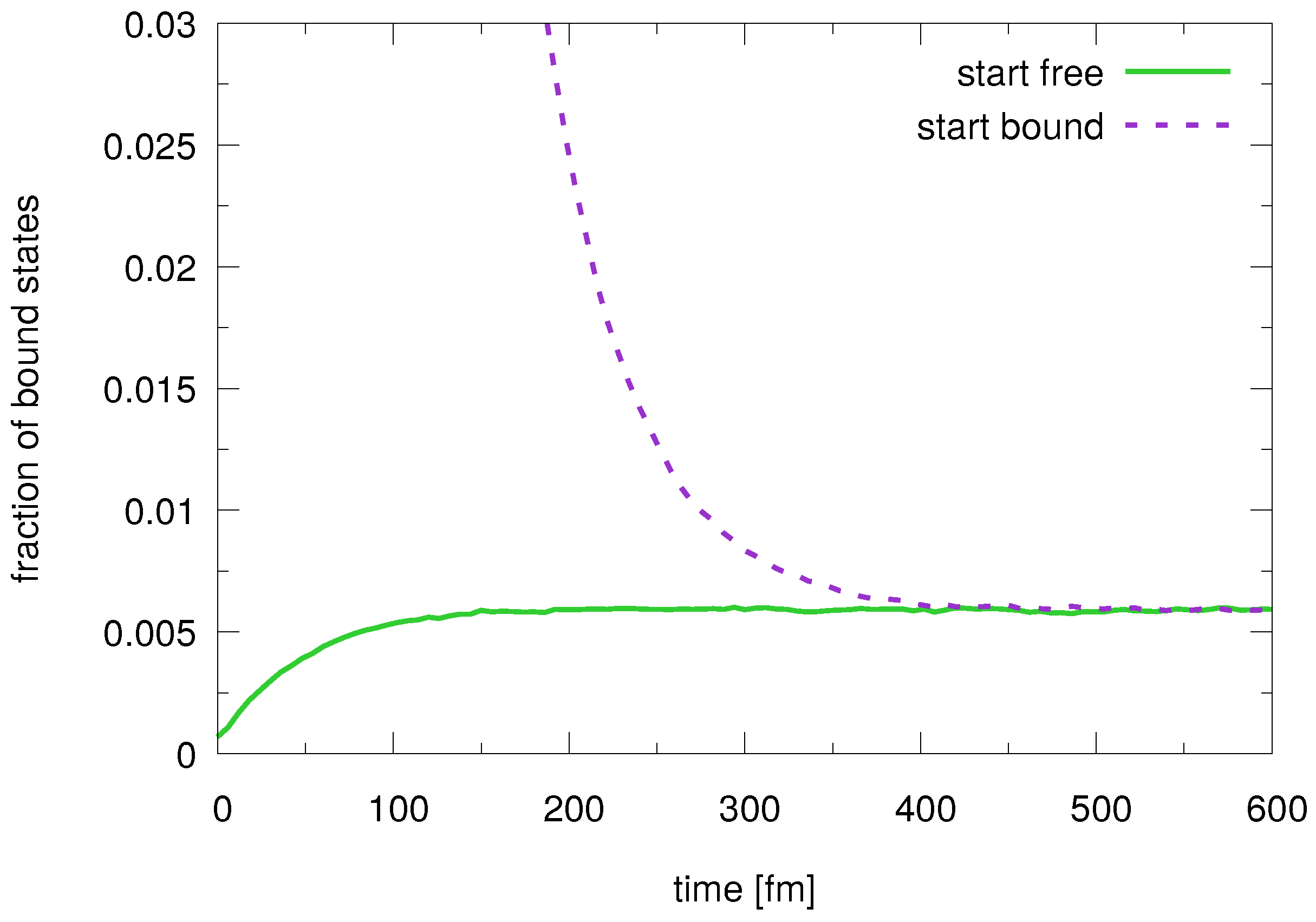
We have also investigated the time evolution of the bound states at a temperature of for two initial conditions.
In the first simulation the charm and anti-charm quarks are initially randomly placed inside the box. For the second simulation the heavy quarks are initially created as bound states with a pair energy of
, which approximately corresponds to the maximum of the peak on the left panel of
Figure 3. The momenta are set back-to-back with a relative velocity that is taken from a Maxwell distribution with its center at the average value of typical relative velocities of charmonium
[
7]. As shown in
Figure 5, in both cases the fraction of bound states in the system equilibrates to the same value as expected. At this point the dissociation and recombination rates are equal and therefore the principle of detailed balance is fulfilled.
To see the influence of the medium’s temperature on the equilibration time we calculated the time evolution at different temperatures. In this simulation we produced five charm-anticharm pairs, initially created as bound states. The results are displayed in
Figure 6.
Larger screening effects at higher temperatures lead to a smaller fraction of bound states at equilibrium. Also the equilibration time decreases. This is expected, because the friction coefficient increases with temperature. The momentum and therefore also the energy transfer in the collisions with the light medium constituents is higher.
To check if our simulation is also in accordance with an equilibrated thermodynamic system, we calculated the particle number using the grand canonical partition function. Since the dissociation and recombination of a
-meson is a process of the kind
the chemical potentials are connected by
which means for the fugacity
. The number of
in the system can then be calculated by knowing the initial number of charm-anticharm-pairs. We compared the results from our simulation with those obtained by using the grand canonical partition function for three different box sizes in
Table 1. We find that both values are of the same order of magnitude.
We could show that our model passes all equilibrium tests. Various extensions are possible to improve the model. The long-time goal of this project is to obtain a full in-medium quantum Langevin treatment of quarkonia.