Abstract
A new form of fragmentation function is presented here, motivated by earlier non-extensive studies of jet fragmentation. We parametrized our Tsallis-like function on pion spectra and compared it to the most common fragmentation function parametrizations. It is shown that the new form is in agreement with earlier parametrizations, furthermore, its scale evolution overlaps better with the experimental data.
1. Introduction
In high energy collisions the energy distribution of the outgoing particles with low transverse momentum ( GeV/c) follows a thermal-like, exponential distribution. Particles with higher transverse momentum ( GeV/c), where perturbative QCD (pQCD) works better, follow power law distributions. The whole spectrum cannot be described by one exponential or power law function, but the Tsallis distribution describes it very well [1].
Statistical systems, like high-energy proton-proton () or electron-positron () collisions are small. The created about 100 particles are far from the thermodynamic limit, highly fluctuating and correlated. Therefore, they could be beyond the validity of statistical mechanics, which was built for weakly interacting systems [2,3,4]. The q entropy is a generalization of Boltzmann’s one, which could lead to a better description of this collision system [5]. The theory has a temperature-like parameter, T and an additional q parameter describing the non-additivity of the entropy for independent systems. Tsallis is the characteristic distribution, derived from this so-called non-extensive entropy, analogue to the Boltzmann distribution. In the limit, Tsallis’ entropy and distribution restores Boltzmann’s.
In Ref. [6], we built a model for jet fragmentation resulting in the so called microcanonical Tsallis distribution, derived from the observed Gamma shape of the multiplicity distribution. This result is extended here, by applying the form as a fragmentation function (FF). Our paper has two aims: (i) to present the validity of our FF assumption by comparing it to widely applied FFs and experimental data, (ii) to investigate the non-extensive parameters of FFs by comparing them to earlier studies [1].
2. The Formalism
In the parton model assuming the factorization, perturbative (e.g., partonic cross sections) and non-perturbative (e.g., parton ditribution and hadronization) processes are treated separately. The normalized cross section of the outgoing h hadrons in annihilation is defined in [7,8] as
where Q is the momentum scale, is the momentum fraction, where hadron energy is and is the center of mass energy. The is the total cross section. The inclusive differential cross section of hadron production is
where functions are calculated from pQCD. The non-perturbative is the fragmentation function, characterizing the probability of an i-type of parton fragmenting into a hadron h at a given z and Q. The Q evolution of the FF is described by DGLAP evolution equations [7],
where run for all (anti)quarks and the gluon. The are the splitting functions from pQCD.
FFs are arbitrary functions satisfying Equation (3) and . The latter is required for the momentum conservation and consequently the probability interpretation. There is no unified theory to determine FFs, thus phenomenological ansatz is used for the form and then it is parametrized with experimental data [8,9]. From Equation (2) one can see that the shape of the hadron spectrum is the result of the convolution integral with the arbitrary shaped FF. Therefore, the spectra are not a pure power law despite the frequently referred statement about pQCD.
The most common FF ansatz is polynomial with Q dependent parameters and ,
Previous studies have determined the parameters of this FF and it uncertainties with experimental data [10,11,12]. This form above works perfectly above 5 GeV/c, however its parameters differ from theoretical expectations, based on the parton splittings [8].
In our previous studies, we determined the parameters of the Tsallis distribution in cases of various spectra for collisions, different hadrons, and kinematic regimes [1]. We determined for at LHC energies, increasing with the collision energy. The temperature-like parameter , weakly depends on the collision energy and in contrast to q, it is independent from the number of valence quarks. We developed a non-extensive jet fragmentation function, the so-called microcanonical Tsallis distribution in Ref. [6] and we postulate the result as an FF ansatz,
where are Q dependent parameters. This FF has the same number of parameters as Equation (4).
3. Results
To obtain the parameters of our FF, we defined Equation (5) at a given . Then we evolved to Q using Equation (3) to minimize the function, by changing the parameters of the FF,
where y and is the measured spectrum value and its uncertainty, and is the number of parameters. We restricted our parameters to be positive, but no further constrains were added, counter to the studies using Equation (4). In this paper, we use data at GeV, from Ref. [10]. We follow all notations and definitions from Ref. [10] in leading order (LO), e.g., independent channels or initial scales GeV for and g, for c and b respectively.
We summarize our first results from minimizing Equation (6). The left panel of Figure 1 shows the measured spectrum and the fit we obtained. As a comparison, we plotted calculations with the HKNS [10] and KKP [11] parametrizations in LO using Equation (4). The smallness of the relative differences highlight that our result is in a good agreement with the data and that there is almost no substantial difference between the various models. The right panel of Figure 1 shows the probability densities, of the fitted microcanonical Tsallis FFs, compared to the HKNS with uncertainties and KKP results at a given Q. The different partonic channels agree mostly, however our formula does not diverge at and its slopes are different. For simplicity, we did not use flavor tagged data in the fit, causing the differences seen in the c and b channels.
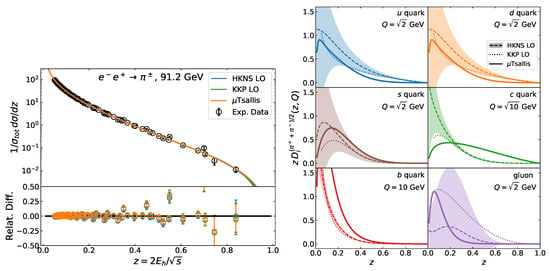
Figure 1.
(Left): The microcanonical Tsallis FF parametrization in pion spectrum from Ref. [10]. HKNS and KKP labels two LO calculations using polynomial FF from Refs. [10,11]. (Right): The microcanonical Tsallis FF parametrization compared to HKNS with uncertainty and KKP FFs for different partonic channels at a given Q.
Figure 2 shows the FF parameters from Equation (4) for HKNS (left) and KKP (middle) and from Equation (5) for microcanonical Tsallis FF (right) parametrization for different Q between GeV. If , then diverges, therefore FF looses the probability interpretation (gray area on Figure 2). With Equation (3), the energy evolution of the pion spectrum from Equation (1) was determined for all three cases. We fitted these spectra with a single function using Equation (4) for HKNS and KKP and Equation (5) for microcanonical Tsallis. On the HKNS and KKP panels one can see, there is a weak correlation between the partonic parameters and parameters obtained from the spectrum fits. However, in the case of the microcanonical Tsallis, the correlation is stronger. In all cases, the FF of u-quark agrees best with the spectra fit, which was expected because of their dominating contribution in pions. For more comparison, we fitted further experimental data with the same way between GeV from Ref. [10], which overlapped with the microcanonical Tsallis description.
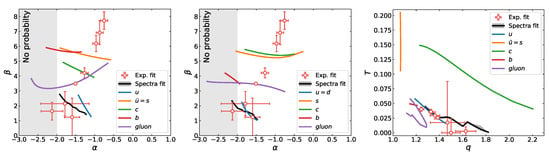
Figure 2.
Parameters of the HKNS (left), KKP (middle) and microcanonical Tsallis FF (right) are plotted for different Q values and partonic channels. Gray area shows where the polynomial FFs loose the probability meaning. Experimental data and the scale evolved spectra was also fitted with a single distribution in respect to Equations (4) and (5), described in the text.
4. Conclusions
In this paper we performed a non-extensive motivated fragmentation function parametrization and we calculated the LO spectra of pions in high-energy collision. We compared and verified our FF with widely used other FF parametrizations and experimental data as well. We obtained that our microcanonical Tsallis FF differs from the HKNS [10] and KKP [11] FFs at lower energy scales and momenta, which could affect the low momentum calculations of proton-proton collisions. The attractor behaviour of the DGLAP evolution could ensure the same behaviour at high Q [13], supporting the power law tailed pQCD observations. Our fragmentation suggests that there could be a more suitable description for the fragmentation, which overlaps better with the experimental data.
Funding
Supported by ÚNKP-18-3 New National Excellence Program of the Ministry of Human Capacities, OTKA K120660, K123815, THOR COST action CA15213, Wigner Data Center and Wigner GPU Laboratory.
Acknowledgments
We would like to thank for Gergely Kalmar and the HKNS group for sharing their software.
References
- Bíró, G.; Barnaföldi, G.G.; Biró, T.S.; Ürmössy, K.; Takacs, A. Systematic Analysis of the Non-Extensive Statistical Approach in High Energy Particle Collisions—Experiment vs. Theory. Entropy 2017, 19, 88. [Google Scholar]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Campa, A.; Dauxois, T.; Fanelli, D.; Ruffo, S. Physics of Long-Range Interacting Systems; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Takacs, A.; Kocsis, B. Isotropic-Nematic Phase Transitions in Gravitational Systems. II. Higher Order Multipoles. Astrophys. J. 2018, 856, 113. [Google Scholar]
- Biró, T.S.; Ván, P.; Barnaföldi, G.G.; Ürmössy, K. Statistical Power Law due to Reservoir Fluctuations and the Universal Thermostat Independence Principle. Entropy 2014, 16, 6497–6514. [Google Scholar] [CrossRef]
- Urmossy, K.; Barnafoldi, G.G.; Biro, T.S. Generalised Tsallis Statistics in Electron-Positron Collisions. Phys. Lett. 2011, B701, 111–116. [Google Scholar]
- Ellis, R.; Stirling, W.; Webber, B. QCD and Collider Physics; Cambridge University Press: Cambridg, UK, 2003. [Google Scholar]
- Patrignani, C. Review of Particle Physics. Chin. Phys. C 2016, 40, 100001. [Google Scholar]
- Bertone, V.; Hartland, N.P.; Nocera, E.R.; Rojo, J.; Rottoli, L. A determination of the fragmentation functions of pions, kaons, and protons with faithful uncertainties. Eur. Phys. J. 2018, C78, 651. [Google Scholar] [CrossRef] [PubMed]
- Hirai, M.; Kumano, S.; Nagai, T.H.; Sudoh, K. Determination of fragmentation functions and their uncertainties. Phys. Rev. 2007, D75, 094009. [Google Scholar] [CrossRef]
- Kniehl, B.A.; Kramer, G.; Potter, B. Fragmentation functions for pions, kaons, and protons at next-to-leading order. Nucl. Phys. 2000, B582, 514. [Google Scholar] [CrossRef]
- de Florian, D.; Sassot, R.; Epele, M.; Hernández-Pinto, R.J.; Stratmann, M. Global analysis of fragmentation functions for pions and kaons and their uncertainties. Phys. Rev. D 2015, 91, 014035. [Google Scholar] [CrossRef]
- Blaizot, J.P.; Mehtar-Tani, Y. Energy flow along the medium-induced parton cascade. Ann. Phys. 2016, 368, 148–176. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).