Coherence Effects in Multiple Medium-Induced Radiation ^†

Abstract

In the first part of this work we study the color coherence phenomenon by considering the well-known quark-antiquark antenna with an in-medium hard gluon emission and an extra very soft emission outside it—double antenna. By discussing the coherence effects in terms of the survival probability, we generalize previous studies of the antenna radiation to the case of more than two emitters. After providing support to the jet quenching picture with effective emitters in the QCD cascade, we present a novel setup of an antenna splitting inside the medium taking into account the finite formation time of the dipole, which turns out to be an important scale. We read into the role of coherence and the relevant time scales which control the scenario, while also providing theoretical support for vacuum-like emissions early in the medium. Finally, by mapping the spectrum of in-medium splittings through the corresponding kinematical Lund diagram, we appreciate regimes of a close correspondence to a semi-classical description.

1. Introduction

The study of jets has turned out into one of the most effective ways to prove the quark-gluon plasma properties in heavy-ion collisions at the LHC. Several approaches try to probe the physics behind jet evolution in matter, but the latest studies of jet substructure are the ones which do it in more detail [1]. However, although detailed analyses of jet substructure shed light on the mechanism of jet-medium interactions, it lacks an accurate description for jet propagation and fragmentation in matter since the problem of parton splittings is crucial in a wide range of high-energy physics scenarios. For instance, the development of a Monte Carlo QCD parton shower requires the splitting vertex along with a calculation of the available phase space.

2. Results

2.1. Double Antenna Radiation

The physical scenario that we present here goes further in the discussion about the coherence effects of QCD radiation when considering in-medium interference processes. In particular, we put forward the extension of the quark-antiquark antenna radiation [2] to a multiple emitters setup with the final goal of extrapolating the results to n-emitters. With this aim, we compute the squared amplitude of the diagrams associated with the processes into consideration—hard and soft gluon radiation off the quark (${\mathcal{R}}_q$), hard gluon radiation off the quark and soft gluon radiation off the antiquark (${\mathcal{R}}_{\overline{q}}$) and hard gluon radiation off the quark and soft gluon radiation off the radiated gluon (${\mathcal{R}}_g$)—as well as the interference terms between these physical processes.

Not surprisingly, the direct terms ${\mathcal{R}}_q$, ${\mathcal{R}}_{\overline{q}}$ and ${\mathcal{R}}_g$ are proportional to a Casimir, i.e., no medium modification is expected. However, we perceive medium modifications explicitly when computing the interference terms between the setups we looked at. For example, considering hard and soft gluon radiation off the quark in amplitude and hard gluon radiation off the quark and soft gluon radiation off the radiated gluon in complex-conjugate amplitude and taking the large-$N_c$ limit, the resulting spectrum is proportional to the convolution of the survival probabilities—which control the stage of color coherence in the soft gluon emission—corresponding to the regions in which the hard splittings take place, as illustrated by Figure 1. Therefore, we recover a novel factorization which remarkably keeps track of the coherence regimes throughout the multiple antennas picture. In other words, the general result of the antenna can be generalized to each of the smaller antennas.

2.2. Finite Formation Time Effects

The generic result introduced above puts forward an interesting extension to the original antenna radiation result [2], but both restrict the problem by not considering the effects of the formation time of the quark-antiquark pair. Let us now consider another scenario to go further in measuring the color coherence phenomena present at jet physics. In order to quantify the finite formation time effects for in-medium splittings, we focus on the splitting of a photon into a quark-antiquark pair—$\gamma \to q\overline{q}$—at a finite distance in the medium as shown in Figure 2 below. It is worthy to point out that in the problem we are raising radiative processes are not taken into account after the formation of the pair. Particularly, we put all our efforts in trying to thoroughly understand the formation of the dipole itself.

Then, considering a singlet antenna with a short formation time and assuming medium averages are local in time, we can treat separately the regions defined by the time-like separation of the splitting vertices in the amplitude and the complex-conjugate amplitude—Region I, between (t,t’)—and the one between the formation time and the end of the medium—Region II, between (t’,L).

In Region I, the Wilson lines—describing the propagation of the partons through the medium— form a dipole with a separation increasing with t, while in Region II we are only left with the average of a trace of four Wilson lines, namely a quadrupole. The appearance of the quadrupole is crucial since it takes into account the in-medium interactions effects from formation time to the end of the medium.

Restricting our study by fixing the trajectories of the particles to follow classical trajectories and neglecting their in-medium transverse momentum broadening, we arrive at a semiclassical picture of the leading partons. The cross section for the splitting process can be written as

$$\frac{d{\sigma }^{med}}{dzd{\overrightarrow{p}}^2}=\frac{d{\sigma }^{vac}}{dzd{\overrightarrow{p}}^2}(1+F_{med}),$$

(1)

where $F_{med}\equiv F_{med}(z,\theta )$ contains all the information about the medium modifications. It reads

$$F_{med}=2{\int }_0^{{\zeta }_L}ds\left[{\int }_0^{{\zeta }_L}d{s}^{\prime }cos(s^{\prime }-s)S_{12}(s^{\prime },s)Q({\zeta }_L,s^{\prime },s)-sin({\zeta }_L-s)S_{12}({\zeta }_L,s)\right],$$

(2)

where $S_{12}(s^{\prime },s)$ and $Q({\zeta }_L,s^{\prime },s)$ are the two- and four-point correlators of Wilson lines which resum medium interactions respectively [3]. In this expression the time coordinates and the intermediate time-integrations are scaled by the formation time, $t_f$, as ${\zeta }_L\equiv L/t_f$ and $s\equiv t/t_f$. The first term in Equation (2) stems from considering an in-medium splitting in both the amplitude and its complex-conjugate, while the second one corresponds to the interference between an in-medium and an outside of the medium splitting.

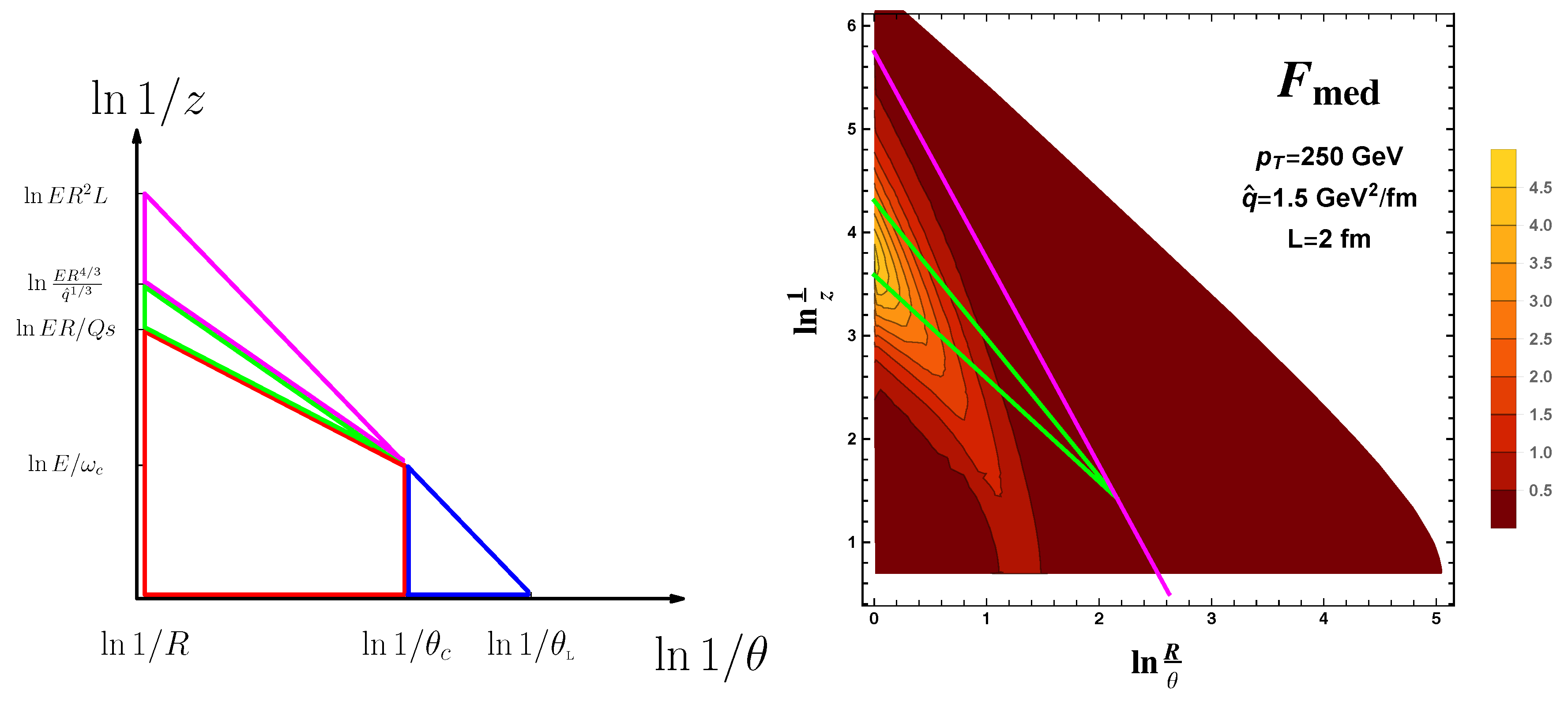
Looking at the analytical expressions of the dipole and the quadrupole, we have elicited four different competing time scales: (i) the formation time $t_f$, (ii) the decoherence time $t_d$, (iii) the broadening time $t_{br}$ and (iv) the length of the medium L.

The decoherence time—$t_d\sim {\left(\frac{1}{\widehat{q}{\theta }^2}\right)}^{1/3}$—controls the color decoherence of the parton pair, while the broadening time—$t_{br}\sim {\left(\frac{1}{\widehat{q}{\theta }^{2}L}\right)}^{1/2}$—governs the transverse momentum broadening through the medium from formation time—$t_f=\frac{2z(1-z)E}{{\overrightarrow{p}}^2}$—to the length of the medium—L. We have drawn the Lund diagram for one splitting in Figure 3 (left panel), where the color areas on the plane are related to the possible time orderings of the scales. Let us get into the details of the regions sketched below:

• (A.1) $t_f<t_{br}<t_d<L$: Particles are created early in the medium but at large angles, so they decohere at a finite distance inside the medium, what corresponds to vacuum-like emissions inside the medium.
• (A.2) $t_{br}<t_f<t_d<L$: In this region, the broadening time is shorter than the quantum-mechanical formation time and thus we expect medium modifications.
• (A.3) $t_{br}<t_d<t_f<L$: In this case, the time ordering implies a strong suppression of the formation of the dipole itself since the decoherence scale controls the stage before formation.
• (A.4) $t_f<L<t_d<t_{br}$: The splitting occurs inside the medium, but at small angles and hence, the created patrons will never decohere in color so that we expect a vacuum emission pattern.
• (B) $t_f>L$: The splitting takes place outside of the medium. Given that, we do not expect medium activity.

All in all, regions (A.1) and (A.4) support the notion of vacuum-like emissions taking place inside of the medium. Finally, we evaluated numerically the medium modification function $F_{med}$ in the Lund plane showed in Figure 3 (left panel), see Figure 3 (right panel), with the final goal of checking the factorization derived in Equation (1). The numerical results are in good agreement with the analytically derived ones since the medium modifications are expected to emerge in regions (A.2) and (A.3).

3. Discussion

The color correlation between highly energetic partons discussed in Section 2 results to be crucial to fully understand jet evolution in QCD matter. The results presented in Section 2.1 show that the two-emitters antenna scenario conclusions can be easily extrapolated to the case of two hard-splittings inside the medium. Additionally, after studying in detail the formation of the antenna itself in Section 2.2, this work also provides support to the idea of in-medium purely vacuum-like emissions, pointing out the importance of the time-scale which controls the splitting process. These developments go further in attaining a complete description of a QCD parton shower.