Testing the Reliability of the Soft-Gluon Approximation for High p⊥ Particles †
Abstract
:1. Introduction
2. Methods
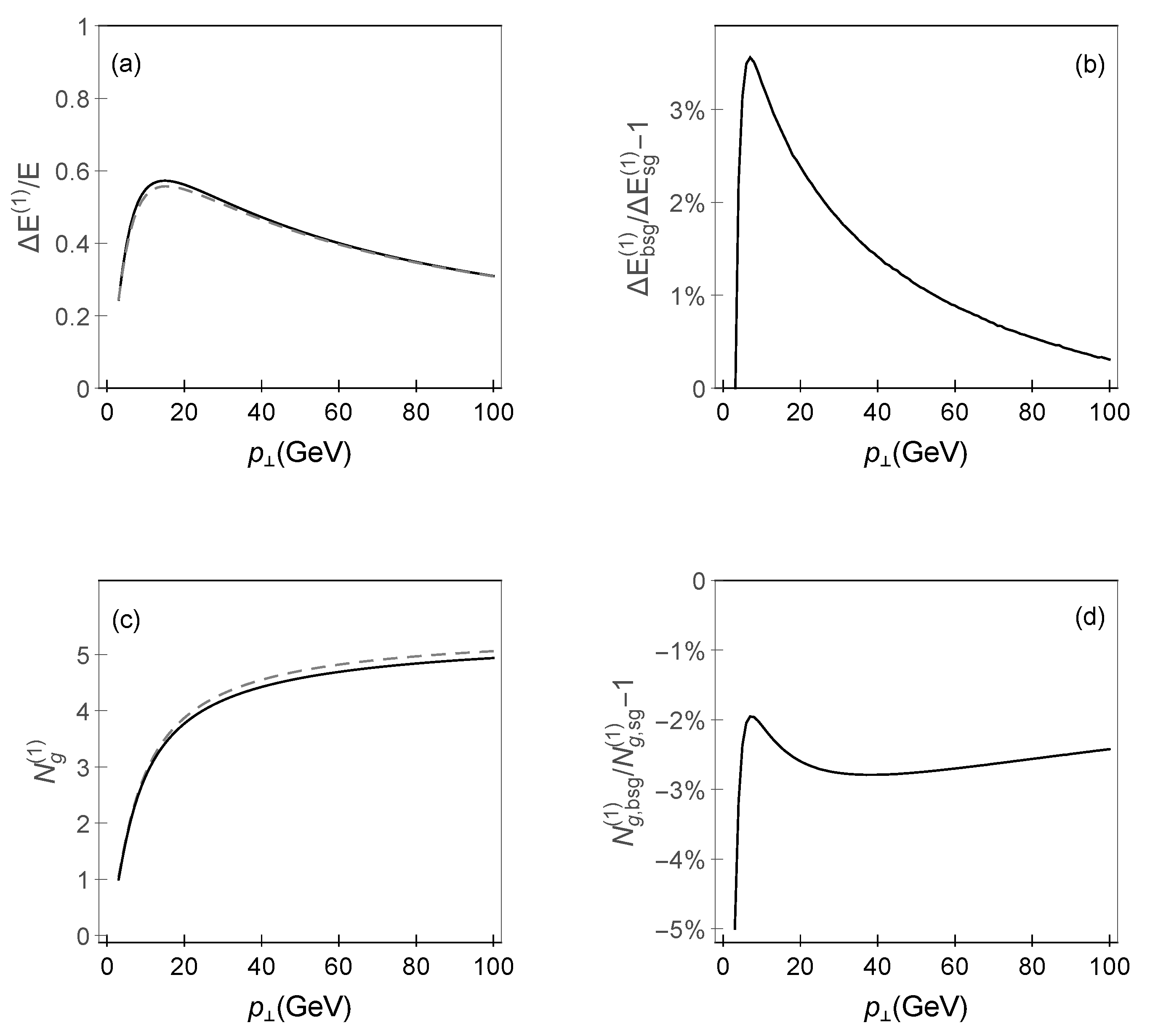
3. Results
4. Discussion
Funding
Conflicts of Interest
References
- Armesto, N.; Salgado, C.A.; Wiedemann, U.A. Medium induced gluon radiation off massive quarks fills the dead cone. Phys. Rev. D 2004, 69, 114003. [Google Scholar] [CrossRef]
- Baier, R.; Dokshitzer, Y.L.; Mueller, A.H.; Peigne, S.; Schiff, D. Radiative energy loss and p(T) broadening of high-energy partons in nuclei. Nucl. Phys. B 1997, 484, 265–282. [Google Scholar] [CrossRef]
- Gyulassy, M.; Levai, P.; Vitev, I. Reaction operator approach to nonAbelian energy loss. Nucl. Phys. B 2001, 594, 371–419. [Google Scholar] [CrossRef]
- Majumder, A.; Van Leeuwen, M. The Theory and Phenomenology of Perturbative QCD Based Jet Quenching. Prog. Part. Nucl. Phys. A 2011, 66, 41–92. [Google Scholar] [CrossRef]
- Apolinario, L.; Armesto, N.; Salgado, C.A. Medium-induced emissions of hard gluons. Phys. Lett. B 2012, 718, 160–168. [Google Scholar] [CrossRef]
- Zhang, B.W.; Wang, X.N. Multiple parton scattering in nuclei: Beyond helicity amplitude approximation. Nucl. Phys. A 2003, 720, 429–451. [Google Scholar] [CrossRef]
- Ovanesyan, G.; Vitev, I. An effective theory for jet propagation in dense QCD matter: Jet broadening and medium-induced bremsstrahlung. JHEP 2011, 1106, 080. [Google Scholar] [CrossRef]
- Ovanesyan, G.; Vitev, I. Medium-induced parton splitting kernels from Soft Collinear Effective Theory with Glauber gluons. Phys. Lett. B 2012, 706, 371–378. [Google Scholar] [CrossRef]
- Djordjevic, M.; Djordjevic, M. LHC jet suppression of light and heavy flavor observables. Phys. Lett. B 2014, 734, 286–289. [Google Scholar] [CrossRef]
- Djordjevic, M.; Djordjevic, M.; Blagojevic, B. RHIC and LHC jet suppression in non-central collisions. Phys. Lett. B 2014, 737, 298–302. [Google Scholar] [CrossRef]
- Blagojevic, B.; Djordjevic, M.; Djordjevic, M. Calculating hard probe radiative energy loss beyond the soft-gluon approximation: Examining the approximation validity. Phys. Rev. C 2019, 99, 024901. [Google Scholar] [CrossRef]
- Djordjevic, M.; Gyulassy, M. Heavy quark radiative energy loss in QCD matter. Nucl. Phys. A 2004, 733, 265–298. [Google Scholar] [CrossRef]
- Gyulassy, M.; Wang, X.N. Multiple collisions and induced gluon Bremsstrahlung in QCD. Nucl. Phys. B 1994, 420, 583–614. [Google Scholar] [CrossRef]
- Djordjevic, M.; Gyulassy, M. The Ter-Mikayelian effect on QCD radiative energy loss. Phys. Rev. C 2003, 68, 034914. [Google Scholar] [CrossRef]
- Dainese, A. Perspectives for the study of charm in-medium quenching at the LHC with ALICE. Eur. Phys. J. C 2004, 33, 495–503. [Google Scholar] [CrossRef]
- Wicks, S.; Horowitz, W.; Djordjevic, M.; Gyulassy, M. Elastic, inelastic, and path length fluctuations in jet tomography. Nucl. Phys. A 2007, 784, 426–442. [Google Scholar] [CrossRef]
- Kang, Z.B.; Vitev, I.; Xing, H. Nuclear modification of high transverse momentum particle production in p+A collisions at RHIC and LHC. Phys. Lett. B 2012, 718, 482–487. [Google Scholar] [CrossRef]
- Sharma, R.; Vitev, I.; Zhang, B.W. Light-cone wave function approach to open heavy flavor dynamics in QCD matter. Phys. Rev. C 2009, 80, 054902. [Google Scholar] [CrossRef]
- Gyulassy, M.; Levai, P.; Vitev, I. Jet tomography of Au+Au reactions including multigluon fluctuations. Phys. Lett. B 2002, 538, 282–288. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blagojevic, B.; Djordjevic, M.; Djordjevic, M. Testing the Reliability of the Soft-Gluon Approximation for High p⊥ Particles . Proceedings 2019, 10, 13. https://doi.org/10.3390/proceedings2019010013
Blagojevic B, Djordjevic M, Djordjevic M. Testing the Reliability of the Soft-Gluon Approximation for High p⊥ Particles . Proceedings. 2019; 10(1):13. https://doi.org/10.3390/proceedings2019010013
Chicago/Turabian StyleBlagojevic, Bojana, Magdalena Djordjevic, and Marko Djordjevic. 2019. "Testing the Reliability of the Soft-Gluon Approximation for High p⊥ Particles " Proceedings 10, no. 1: 13. https://doi.org/10.3390/proceedings2019010013
APA StyleBlagojevic, B., Djordjevic, M., & Djordjevic, M. (2019). Testing the Reliability of the Soft-Gluon Approximation for High p⊥ Particles . Proceedings, 10(1), 13. https://doi.org/10.3390/proceedings2019010013




