Detection of Self-Mixing Interferometric Fringes of a Laser Sensor Using Matched Filter †
Abstract
:1. Introduction
2. Self-Mixing Interferometry
3. MF Based Fringe Detection
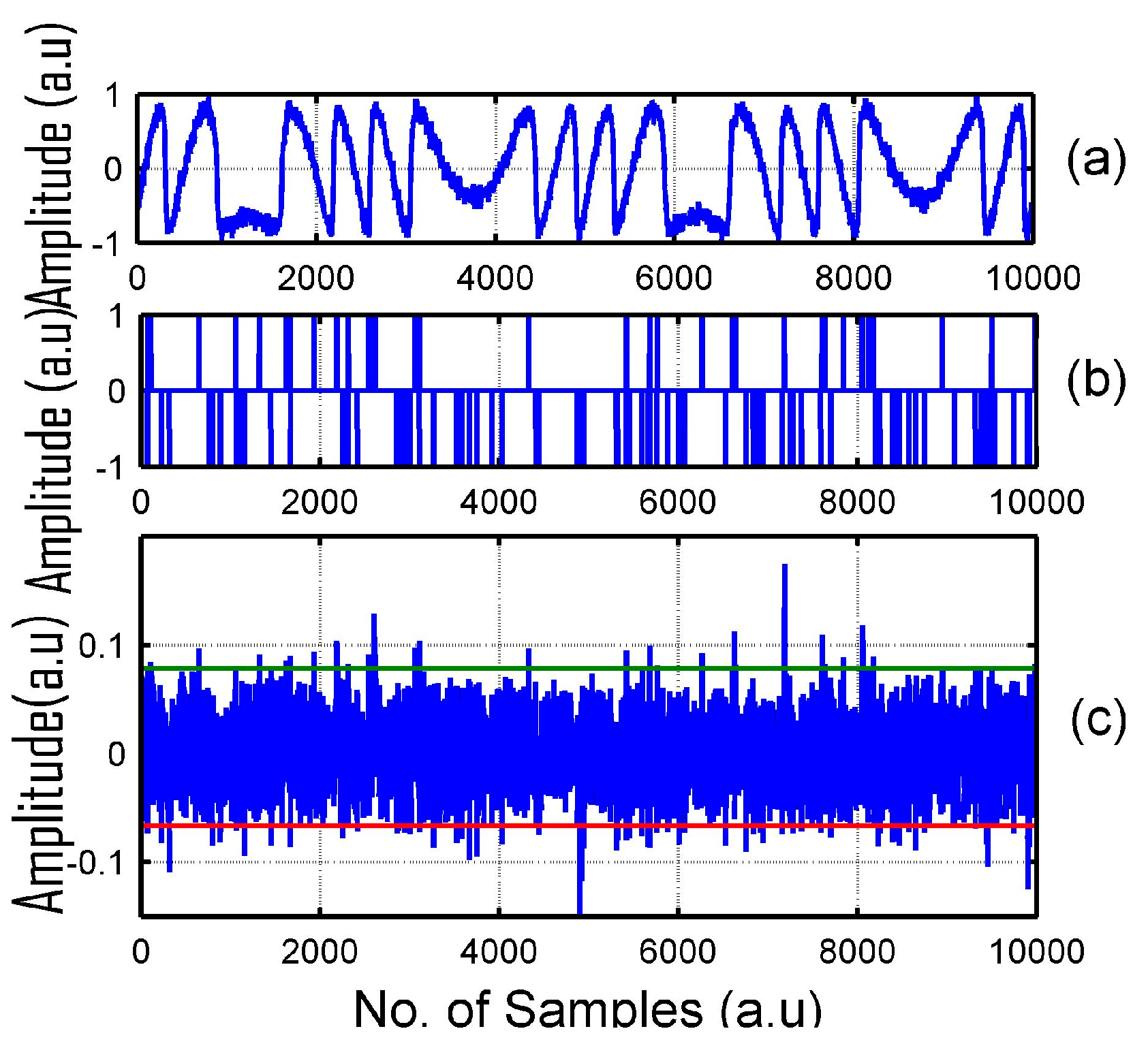
4. Results
5. Conclusions
Conflicts of Interest
References
- Taimre, T.; Nikolić, M.; Bertling, K.; Lim, Y.L.; Bosch, T.; Rakic, A.D. Laser feedback interferometry: A tutorial on the self-mixing effect for coherent sensing. OSA 2015, 7, 570–631. [Google Scholar] [CrossRef]
- Khan, Z.A.; Zabit, U.; Bernal, O.D.; Ullah, M.O.; Bosch, T. Adaptive Cancellation of Parasitic Vibrations Affecting a Self-Mixing Interferometric Laser Sensor. IEEE Trans. Instrum. Meas. 2017, 66, 332–339. [Google Scholar] [CrossRef]
- Donati, S.; Norgia, M. Self-Mixing Interferometry for Biomedical Signals Sensing. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 104–111. [Google Scholar] [CrossRef]
- Bes, C.; Plantier, G.; Bosch, T. Displacement measurements using a self-mixing laser diode under moderate feedback. IEEE Trans. Instrum. Meas. 2006, 55, 1101–1105. [Google Scholar] [CrossRef]
- Zabit, U.; Bernal, O.D.; Bosch, T. Self-mixing Sensor for Real-time Measurement of Harmonic and Arbitrary Displacements. In Proceedings of the 2012 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Graz, Austria, 13–16 May 2012; pp. 754–758. [Google Scholar]
- Bernal, O.; Zabit, U.; Bosch, T. Robust method of stabilization of optical feedback regime by using adaptive optics for a self-mixing microinterferometer laser displacement sensor. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 1–8. [Google Scholar] [CrossRef]
- Arriaga, A.L.; Bony, F.; Bosch, T. Real-time algorithm for versatile displacement sensors based on self-mixing interferometry. IEEE Sens. J. 2016, 16, 195–202. [Google Scholar] [CrossRef]
- Bernal, O.D.; Seat, H.C.; Zabit, U.; Surre, F.; Bosch, T. Robust Detection of Non Regular Interferometric Fringes from a Self-Mixing Displacement Sensor using Bi-Wavelet. Transform. IEEE Sens. J. 2016, 16, 7903–7910. [Google Scholar] [CrossRef]
- Bernal, O.D.; Zabit, U.; Bosch, T. Classification of laser self-mixing interferometric signal under moderate feedback. Appl. Opt. 2014, 53, 702–708. [Google Scholar] [CrossRef] [PubMed]
- Atashkhooei, R.; Royo, S.; Azcona, F.; Zabit, U. Analysis and control of speckle effects in self-mixing interferometry. Proc. IEEE Sens. 2011. Available online: http://ieeexplore.ieee.org/document/6127054/ (accessed on 23 June 2017).
- Kay, S.M. Deterministic Signals. In Fundamentals of Statistical Signal Processing: Detection Theory, 1st ed.; Oppenheim, A.V., Ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1998; Volume 2, pp. 94–101. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akmal, M.; Zabit, U.; Bernal, O.D.; Bosch, T. Detection of Self-Mixing Interferometric Fringes of a Laser Sensor Using Matched Filter. Proceedings 2017, 1, 590. https://doi.org/10.3390/proceedings1040590
Akmal M, Zabit U, Bernal OD, Bosch T. Detection of Self-Mixing Interferometric Fringes of a Laser Sensor Using Matched Filter. Proceedings. 2017; 1(4):590. https://doi.org/10.3390/proceedings1040590
Chicago/Turabian StyleAkmal, Muhammad, Usman Zabit, Olivier D. Bernal, and Thierry Bosch. 2017. "Detection of Self-Mixing Interferometric Fringes of a Laser Sensor Using Matched Filter" Proceedings 1, no. 4: 590. https://doi.org/10.3390/proceedings1040590
APA StyleAkmal, M., Zabit, U., Bernal, O. D., & Bosch, T. (2017). Detection of Self-Mixing Interferometric Fringes of a Laser Sensor Using Matched Filter. Proceedings, 1(4), 590. https://doi.org/10.3390/proceedings1040590




