Photonic Gas Sensor Using a Silicon Strip Waveguide ^†

Abstract

Sensing of gases is a promising area for applications of photonic systems operating in the mid-infrared spectral range. We present an infrared evanescent-field absorption gas sensor based on a silicon strip waveguide, which was specifically designed for CO₂ sensing. We discuss finite element simulations that were used to design the strip waveguide and furthermore present experimental data of quantitative CO₂ measurements with the devised structures. The first demonstrator device detects concentrations down to 5000 ppm CO₂ which is the workplace exposure limit in most jurisdictions.

1. Introduction

We present an infrared-absorption sensor for gas detection based on evanescent-field absorption using a silicon strip waveguide. Due to the sub-wavelength dimensions of the dielectric waveguide, a small fraction of the electromagnetic (EM) modes that propagate along the waveguide also extend outside of the waveguide. The amount of this so called evanescent field, expressed in terms of the evanescent field ratio (EFR), depends on the cross section of the waveguide with respect to the wavelength of the propagating light, as well as on the optical properties of the used materials [1]. A high EFR and low intrinsic damping is crucial for gas sensing since the absorption coefficients are rather low for most gases. If an absorbing medium is brought in the vicinity of the waveguide, the evanescent field is absorbed by the gas attenuating the guided wave, which is detected in terms of a reduced intensity at the output port of the waveguide. Using waveguides for sensors allows incorporating long interactions paths for gas sensing into a small area by using structures like spirals, meanders, or resonators. Small dimensions are crucial for semiconductor mass production and our goal is to develop a fully integrated CMOS compatible sensor.

2. Modeling and Design

The devised sensor test structures are silicon strip waveguides with a length of about 1 cm which were designed for CO₂ sensing. A taper and a launch-pad were added on both ends of the waveguide. On the launch-pad, a grating coupler is placed in order to couple mid-infrared radiation (MIR) from an external MIR source into the waveguide and to out-couple the light onto a detector. The design of the grating coupler, using two dimensional finite element models, was described in [2]. 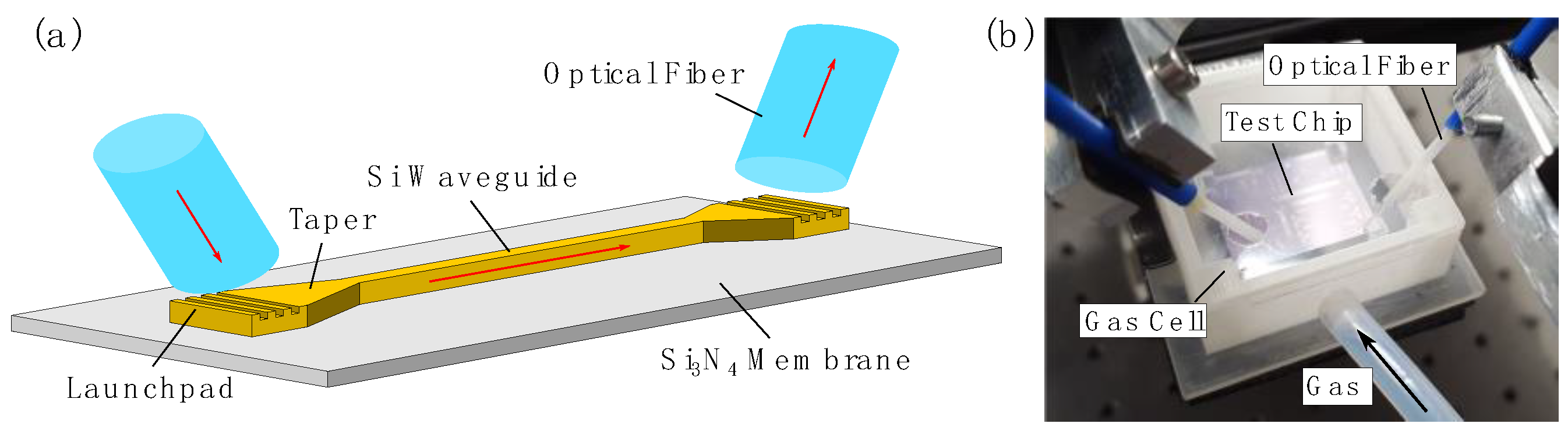Figure 1 shows a schematic representation of the measurement configuration and a gas cell with a test chip, as it was used for the experiments.

The sensor structures were designed for a wavelength of λ = 4.26 µm which is at the center of the CO₂ absorption band. It is expected that an integrated IR source which could be used in the final sensor system will have a rather wide bandwidth that covers the whole CO₂ absorption band. Therefore one needs to design the sensor for the center wavelength of the CO₂ absorption band. A model of the strip waveguide was developed using the finite element method simulation tool COMSOL Multiphysics 5.2a. The material parameters were obtained from the literature [3,4]. A mode analysis was carried out on the cross-section of the waveguide. 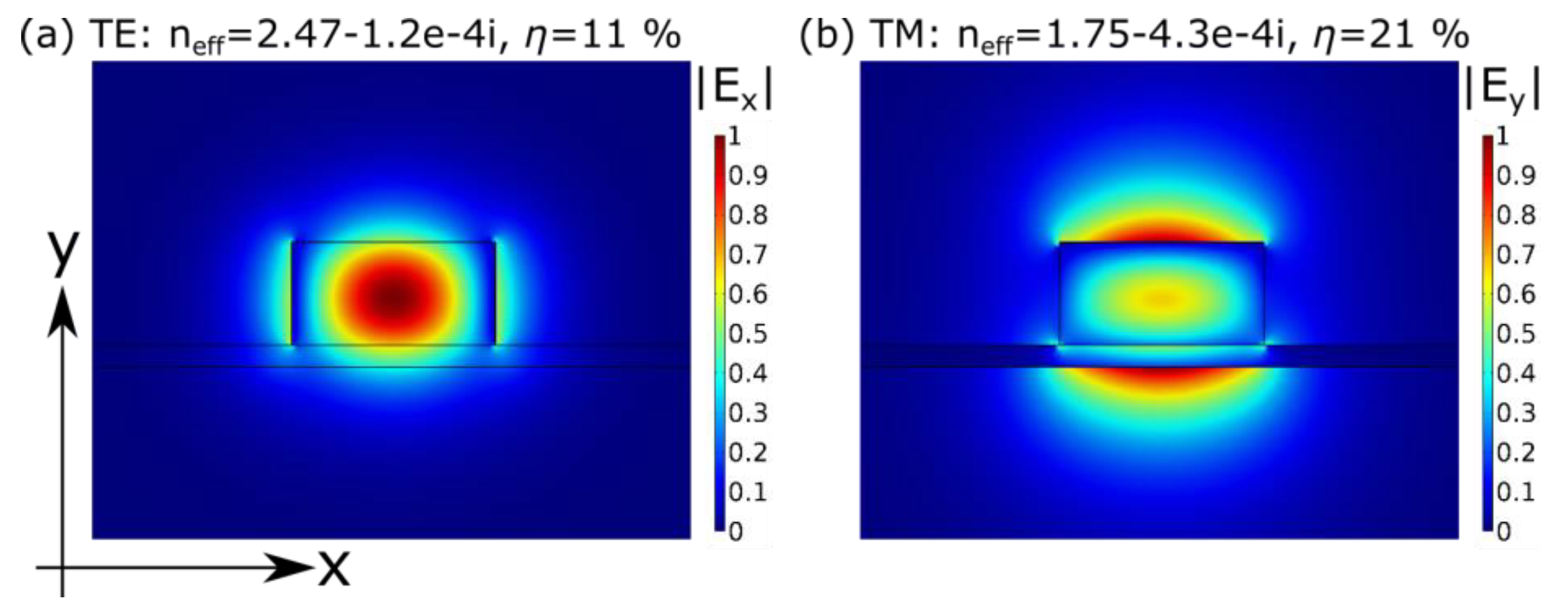Figure 2 shows the normalized electric field distribution of the dominant coordinate |Ex| and |Ey|, respectively, for the fundamental quasi-TE (Figure 2a) and the fundamental quasi-TM mode (Figure 2b). The silicon strip waveguide is located on a thin Si₃N₄ membrane and the rest of the domain is filled by air/gas. For the simulation the domain size was chosen much bigger than shown in Figure 2 to avoid spurious effects at the boundary of the simulation domain.

The (bulk) refractive index of a material $n=n^{\prime }-i·n^{″}$ is a complex material property. It consists of the real part $n^{\prime }$ which indicates the phase velocity or the wavenumber of a plane wave, in said material, and an imaginary part characterized by $n^{″}$, the so called extinction coefficient, which accounts for attenuation (absorption) in the material. The wavenumber and the attenuation of a guided mode can in a similar manner be related to an effective index ${\mathrm{n}}_{\mathrm{eff}}$ and the condition for guided modes is given by [1]:

$${n^{\prime }}_{waveguide}>{n^{\prime }}_{eff}>{n^{\prime }}_{cladding}$$

(1)

If ${n^{\prime }}_{\mathrm{eff}}$ is smaller than ${n^{\prime }}_{\mathrm{cladding}}$, the mode becomes unguided meaning the EM field is oscillatory and not exponentially decaying (evanescent) in the cladding region, leading to an EM field that leaks out into a radiation mode. From the simulation the effective index was evaluated for the two modes and is also shown in Figure 2. At λ = 4.26 µm the real part of the refractive index for Si₃N₄ is $n^{\prime }$ = 2.38 [3]. According to Equation (1), the EM field of the fundamental quasi-TE mode ($n^{\prime }$ = 2.47) is therefore oscillatory in the silicon strip waveguide only and it is evanescent in the Si₃N₄ ($n^{\prime }$ = 2.38) and gas/air region ($n^{\prime }$ = 1). The situation for the fundamental quasi-TM is different since $n^{\prime }$ = 1.75 < 2.38. Thus the quasi-TM mode also extends to the lossy Si₃N₄ membrane. As a consequence the quasi-TM mode has an extinction coefficient that is almost four times higher than the extinction coefficient of the quasi-TE mode. Therefore the transmitted power over the 1 cm long waveguide of the quasi-TM mode is negligible. The EFR η is a measure for the fraction of the EM field that can be used for absorption sensing. It was evaluated from the simulation results as the ratio of the field power in the air/gas area to the total modal power [5]. The evaluated η for the two modes is also shown in Figure 2. The quasi-TM mode reaches almost twice the η as the quasi-TE, but as already explained, the transmitted power of the quasi-TM mode is negligible and it will not contribute to sensing.

3. Experimental

The structures were fabricated on eight inch Si wafers, using standard semiconductor processes leading to polycrystalline silicon strip waveguides on a Si₃N₄ membrane. The membrane was located on a Si/SiO₂ support structure. The fabrication of structures with a similar layer configuration is described in detail in [6].

The CO₂ measurements were carried out using a custom test-bench which was described in [7]. For the quantitative gas measurements, the whole test chip was placed in a 3D printed gas cell (acrylate-type plastic) which was flushed with CO₂/N₂ mixtures at a total flow rate of 100 mL/min (see also Figure 1). To account for the free-beam absorption between the fiber and the launch-pad which happens on both ends of the sensor, a reference measurement was performed and the results were corrected accordingly.

4. Results and Discussion

For the quantitative measurements, the QCL was tuned to 2362.8 cm⁻¹ which corresponds to a wavelength of λ = 4.23 µm and is the position of the CO₂ line with the highest absorption. The time dependent intensity at the output port was recorded, while the gas cell was successively flushed with pure N₂ and a N₂/CO₂ mixture. Although the system reacts immediately to a change of gas concentration due to the sensing principle, every mixture was flushed for a rather long time of 10 min through the cell since a low total flow rate of 100 mL/min was used. 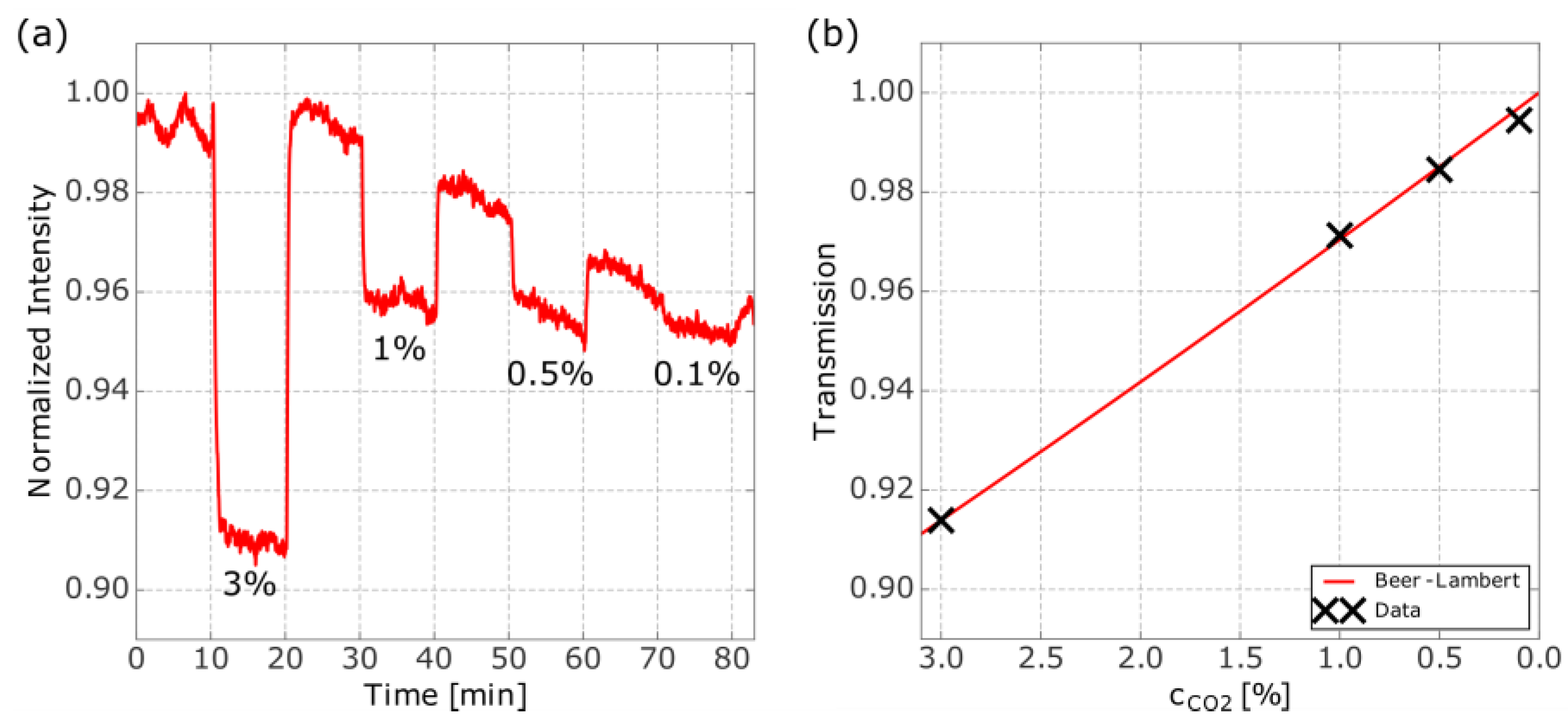The result is plotted in Figure 3a.

The baseline intensity decreased during the measurement due to micro-drift of the used stages (which was not eliminated in Figure 3a). The results show that a concentration of 0.5% (or 5000 ppm) CO₂ can be detected. This is a significant improvement of one order of magnitude, compared to previous work where silicon slab waveguides were used [7]. Even for 0.1% the change in intensity is visible but close to the noise level. The transmission was calculated for the different CO₂ concentrations, where the baseline drift was taken into account. The result is plotted in Figure 3b.

The Beer-Lambert law adapted for our sensor was used to evaluate the possibility for quantitative measurements and converted in order to calculate the absorption coefficient α:

$$I=I_0·e^{-\eta ·c·\alpha ·z} \to \alpha =-\frac{ln\left(\frac{I}{I_0}\right)}{\eta ·c·z}=-\frac{ln\left(T\right)}{\eta ·c·z}$$

(2)

The parameters that were used to calculate α are the transmission T = 0.91, which is the ratio of the transmitted power and the initial power, which was measured for a CO₂ concentration of c = 3%, the evanescent field ratio η = 11% (for the quasi-TE mode) and the path length z = 1 cm (which is the length of the strip). The absorption coefficient was determined as α = 27 cm⁻¹ and with this the transmission according to the Beer-Lambert law was calculated. This is in good agreement with the other experimental data-points as shown in Figure 3b.

When estimating an effective absorption coefficient from literature data [8] taking into account the exact center-wavelength and linewidth of the laser spectrum we obtain an estimated value of α_est = 74 cm⁻¹. The absorption coefficient evaluated from the experimental data was two to three times less than the estimated one, which is probably caused by an EFR which is lower than shown by simulation. This can be due to several reasons, including slightly different dimensions of the fabricated structures and material parameters that differ from literature values.

5. Conclusions

In this work we presented a gas sensor using a sub-wavelength silicon strip waveguide on a Si₃N₄ membrane. The strip waveguides were designed using a finite element method model. The sensor was fabricated with standard silicon MEMS technology and is therefore suitable for semiconductor mass production. Quantitative CO₂ measurements were performed down to 5000 ppm, which is the workplace exposure limit in most jurisdictions. Future work will investigate the intrinsic damping properties of such waveguides in order to be able to enhance the interaction length and therefore to further improve the performance of the sensor.