Wireless Sensing System for Long-Time Assistance in the Parkinson’s Disease ^†

Abstract

A non-invasive wearable wireless sensing system for assisting patients affected by Parkinson’s Disease is proposed. It uses inertial sensors to recognize gait states and involuntary gait freezing. The system is designed for indoor and outdoor long-time monitoring and realizes an individual electronic diary useful for doctors for estimating better the stage of the disease and customizing the pharmacological therapy. Standard tests were performed on a noticeable number of patients. The system performances are the state-of-art in the detection of specific movement disorders of PD patients. The algorithm demonstrated its reliability and robustness respect to individual specific gait and postural behaviors.

1. Introduction

The implications of new technologies involving the use of wearable sensors are becoming increasingly important in healthcare. Information extrapolated from accelerometers and gyroscopes allows a correct reconstruction of the movements and a precise evaluation of the state of the musculoskeletal apparatus. In this frame, patients affected by the Parkinson’s Disease (PD) can benefit mostly from those technological advancements, since PD brings severe ailments and disturbs related to the musculoskeletal apparatus, which include muscular rigidity, tremors, postural instability, bradykinesia, hypokinesia and akinesia [1]. These symptoms vary from one patient to another, are very sensitive to the drug therapy and to the environmental inputs and depend on the progression of the disease. Today, the standard examination of the stage of the disease is done by doctors with the aid of patient and relative reports, which are generally incomplete and arbitrary. In this context, it is easy to understand that a wearable electronic system for monitoring automatically and objectively the motor symptoms of PD patients is strongly desired. The processed data would help doctors in estimating better the disease stage and customizing the pharmacological therapy. The latter point is crucial to mitigate the symptoms and reduce episodes of freezing of gait (FoG). FoG is an involuntary block of movement which can be accentuated by an incorrect drug therapy. It is described by patients as their feet were “stuck on the ground”. In these situations, the patient reacts attempting to make steps, forcing on the lower limbs, thrusting forward the trunk. For this reason, FoG is reported as the main cause of falls of PD patients. It has been demonstrated that a rhythmic sensory stimulation can release the involuntary block [2]. Therefore, a non-invasive wearable system able to provide a reliable detection of the FoG in any context, and timely give a sensorial stimulation would be extremely useful for reducing the catastrophic consequences of falls. Furthermore, a patient electronic diary would help doctors customizing finely the therapy and assessing the disease stage.

2. Materials and Methods

The system consists on two IMU sensors, wireless connected to a portable receiver (a smartphone) and/or directly to a PC collecting data for off-line processing and creating an individual electronic diary (e-diary). The system is depicted in Figure 1. The direct wireless connection to the PC via the home Wifi is preferred in indoor application. The board is a prototype system-on-board designed for processing signals in real-time and transmitting them. The IMU integrates a ±16 g (g-force) 3D accelerometer, and a ±2000 dps 3D gyroscope. The Bluetooth V3.0 module uses the Serial Port Profile (SPP). The processing unit is an ultralow-power 32-bit microcontroller with 33.3 DMIPS peak computation capability and an extremely low power consumption scalable down to 233 uA/MHz. The board size is 25 × 30 × 4 mm³ including the battery. An USB port is included for recharging battery. The PC makes off-line data processing, realizing a friendly interface with remote access to data in a cloud.

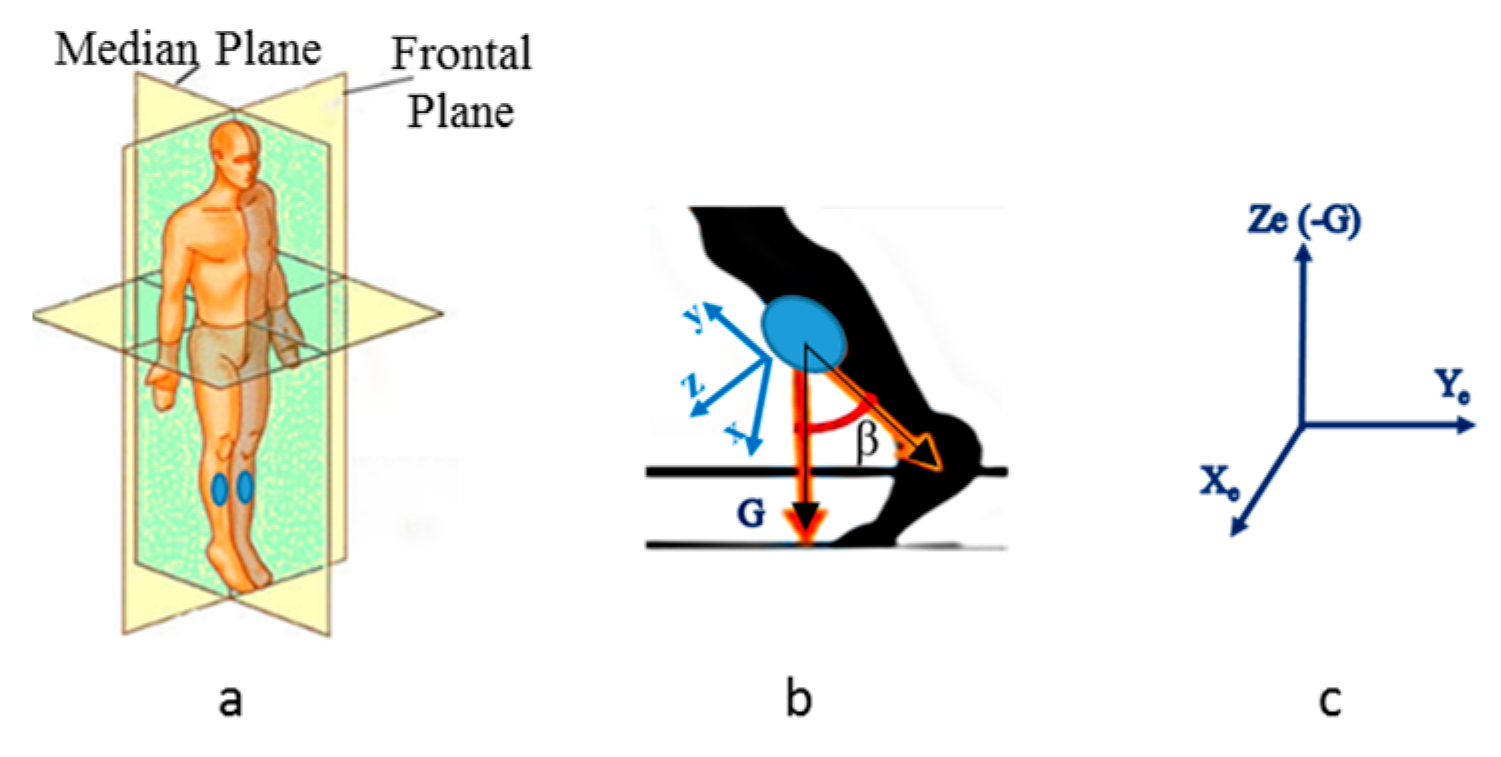
The algorithm is based on a time domain signal analysis. The raw signals of accelerometers and gyroscopes are fused together by using an orientation-estimation algorithm [3]. The sampling frequency (fs) is 60 Hz when a PC is used and 25 Hz when a smartphone is used. Two sensors are positioned on the shins. Gait direction is in the median plane of Figure 2a. The x-y-z sensor reference system sketched in Figure 2b rotates in the Xe-Ye-Ze earth reference system (Figure 2c). Ze coincides with negative G axis. We focus onto the angle β sketched in Figure 2b. It is calculated as the angle formed between two 3D vectors: the negative y-axis and the gravity axis (G). Therefore, the angle β is solid and we need to analyze its projection onto the median plane. Eventual discontinuities of the β angle when it changes the sign, and consequent problems in angle derivation, can be easily overcome by conventional mathematical techniques. The algorithm calculates the first order low-pass filtered angular velocities ω_right, ω_left obtained by β derivation. We define with ω_t and k_t, respectively, the angular velocity and the lowpass filter measured at time t, with k_t-1 the k value at the previous step, with α the smoothing coefficient, with f_cutoff the cutoff frequency:

$$\begin{gathered} kright/left=lowpass(\left|\omega right/left\right|); kt=(1-\alpha )\cdot \omega t+\alpha \cdot kt-1; \alpha ={(1+2\pi \cdot fcutoff/fs)}^{-1}; \\ K=kleft+kright \end{gathered}$$

(1)

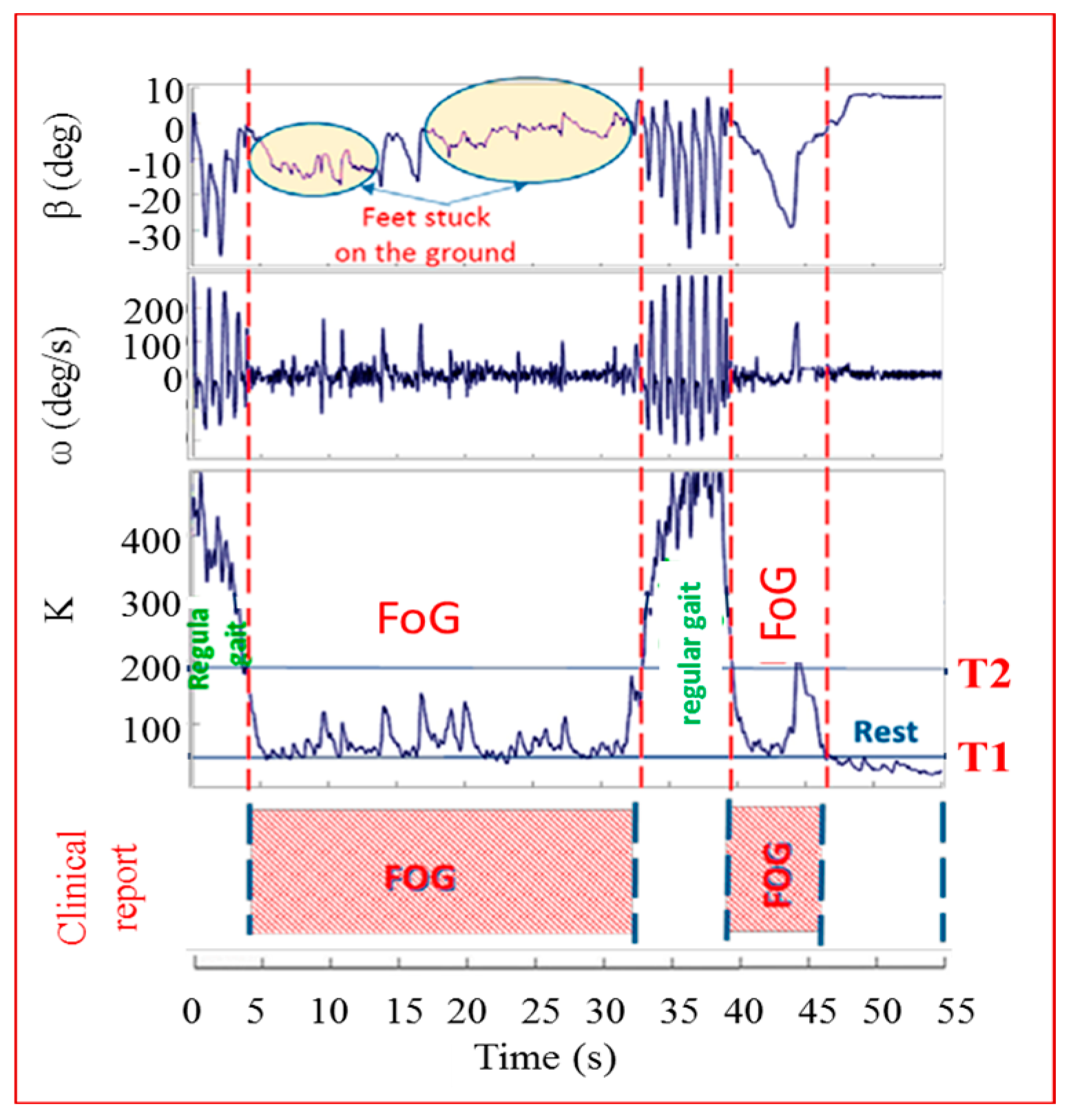
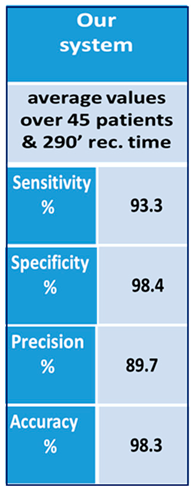
A group of 45 patients of different age, stage of disease and gender was asked to wear the sensors and walk some steps, turn and go back passing through an open door (which is a virtual obstacle inducing FoG). All the tests were filmed and the films were studied by doctors who determined the exact starting and ending times of the FoG episodes. Clinical reports represented our absolute reference. In Figure 3 we can see how the algorithm works. In that test the patient was a female, over 65, in an advanced stage of the disease. The behavior of β, ω and K are shown as function of the test time. As one can see, the β and ω curves varied consistently with time. In particular, it is easy to appreciate an oscillatory behavior of β and ω during the regular gait (0–4 s; 32–39 s) and a flatness during the rest state (46–55 s). The clinical report about the exact FoG timing is indicated in the figure bottom. Doctors referred the occurrence of two FoG episodes, in 4–32 s and 39–46 s. The comparison between the K index and the clinical report allowed defining the T thresholds for the three states classification, as reported in the figure: regular gait (K > T2), FoG state (T2 > K > T1) and rest state (K < T1). Once the values of T1–T2 are fixed for a certain patient, they remain unchanged. A strength of this systems is the possibility to distinguish definitely between the voluntary rest state and the FoG thanks to the fact that sensors on the shins are able to detect any least activity related to leg tremors occurring during FoG times, but not during voluntary rest. This is evident in Figure 3. 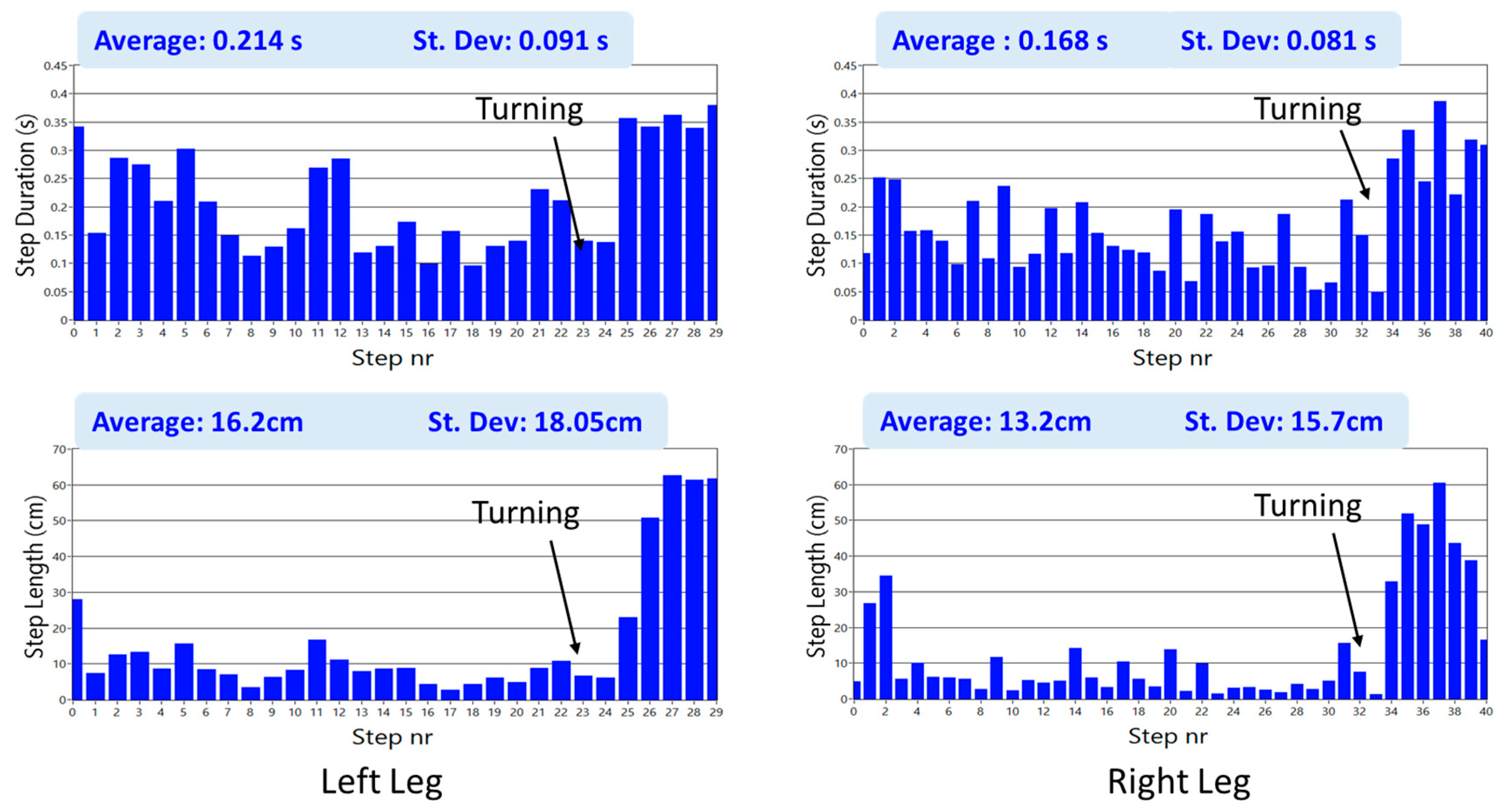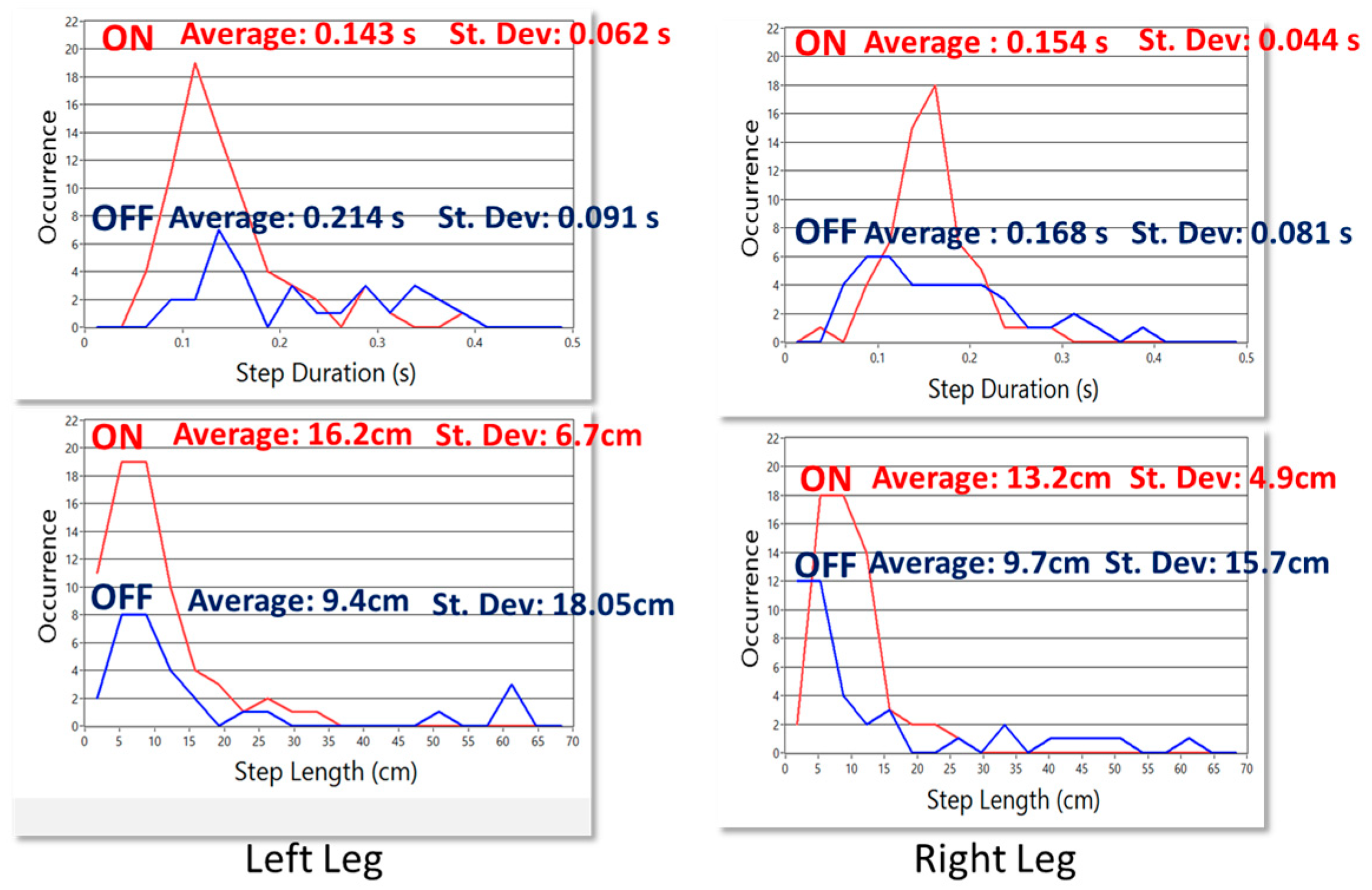To further improve the algorithm and reduce false positives and negatives in FOG detection we introduced two more indices, K_turn and K_swing, especially useful during step shortening associated to turning and in the case of leg tremor due to voluntary body swinging. They are defined as: K_turn = lowpass(|ωy|) and K_swing = lowpass(|ω_Z|). K, K_turn and K_swing indices are calculated, K_turn index is compared with a threshold T_turn and, only in the case K_turn > T_turn, a final index K’ = K + K_turn is calculated. K’ index is then compared with K_swing index and, if K’ < K_swing, the algorithm excludes a body swing and classifies a specific gait state. If K’ > K_swing, the leg movement is interpreted as a body swing.

3. Results and Discussion

The system performance in FoG detection is evaluated averaging over 45 patients (of different age, stage of disease, gender) and 290’ recording times. Results are shown in

Table 1. System performance.

. As a result, our system reported only 6.7% false negative and 1.6% false positive on the overall FoG time. Also 9 healthy persons were studied and we verified the same least occurrence of false positive (1.6%). This is the state-of-art in FoG detection. To realize the e-diary, we evaluated kinematic parameters, as the step length and step duration of the two legs, together with basic statistics outlining eventual leg asymmetry and step uncertainty. Results are shown in Figure 4. The efficacy of the drug therapy during the day can be understood considering the step features before and after the drug administration, as shown in Figure 5. All those results are noticeably interesting to doctors for closely customizing the therapy. Finally, the system can also help doctors in evaluating the disease progress by comparing results on a timescale of months/years.