Contactless Interrogation System for Capacitive Sensors with Time-Gated Technique †
Abstract
:1. Introduction
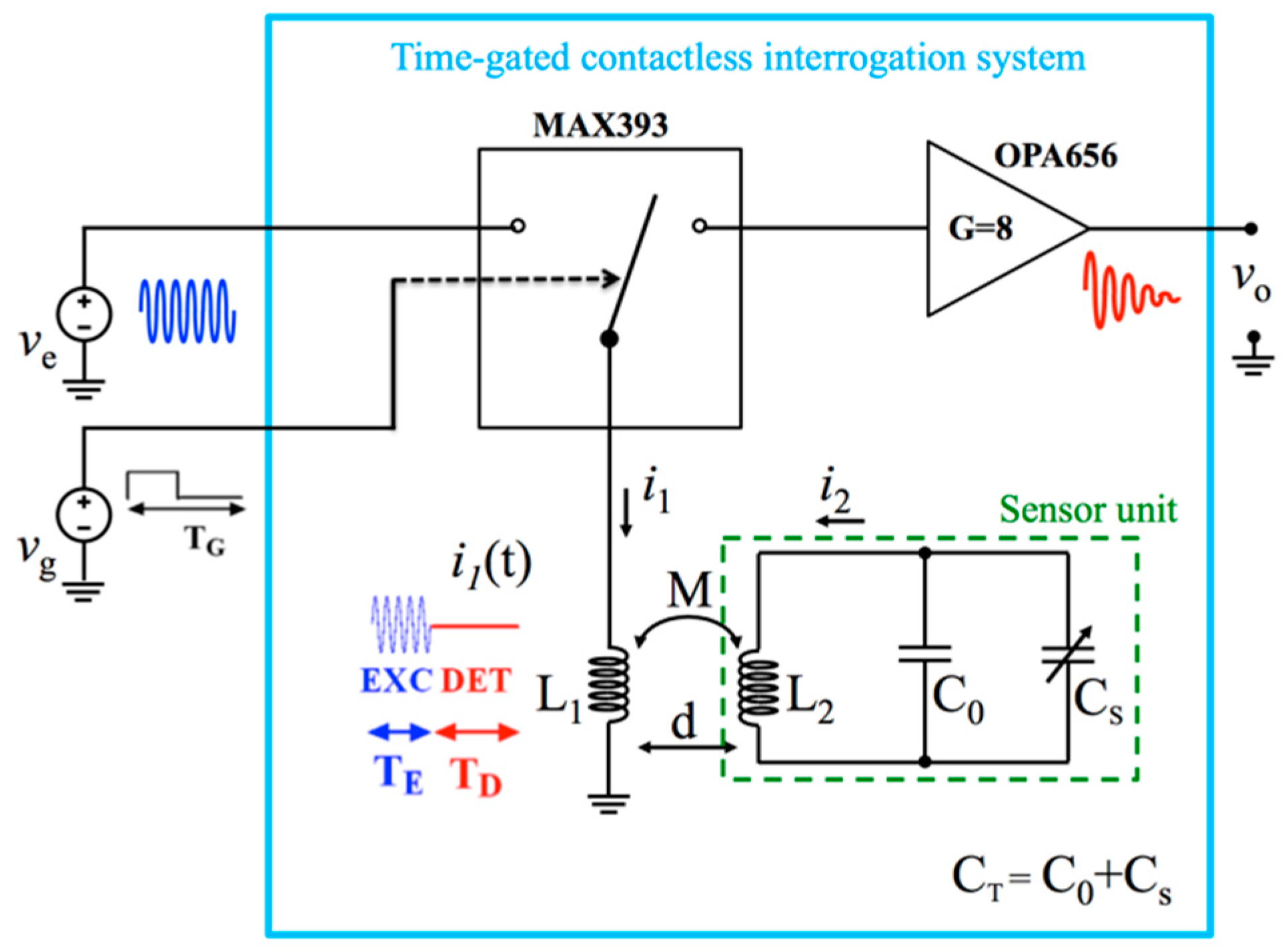
2. Time-Gated Contactless Interrogation System for Capacitive Sensors
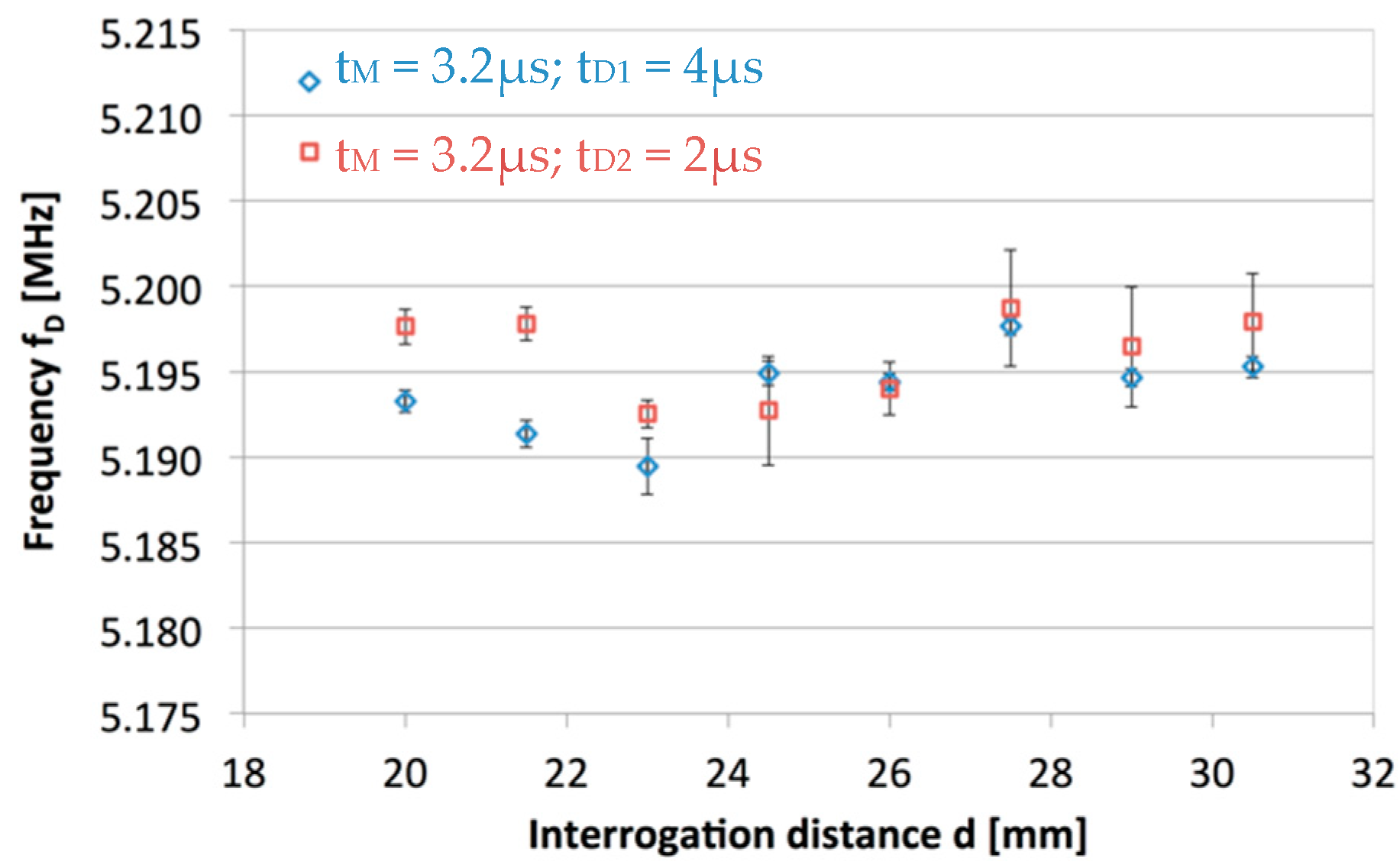
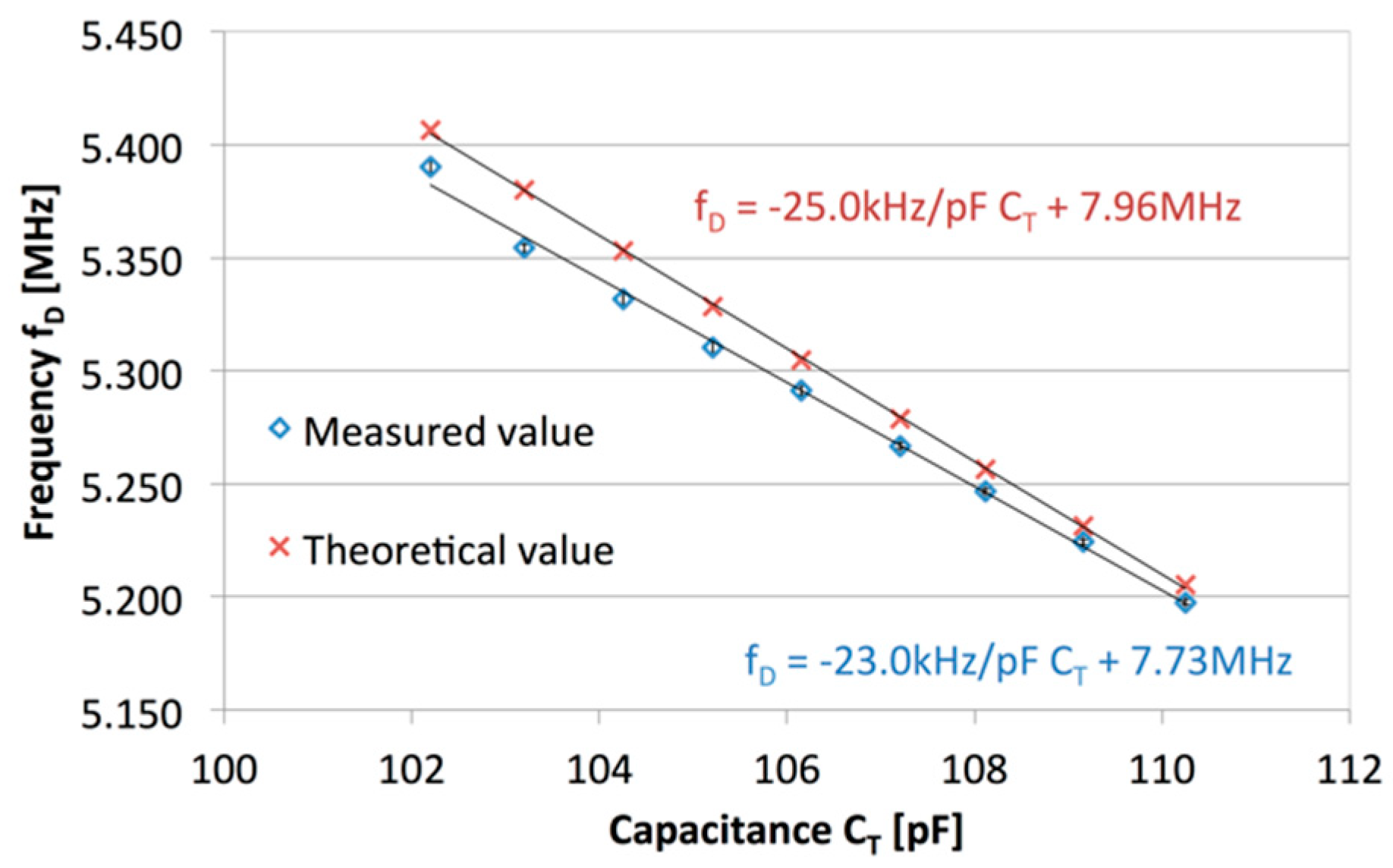
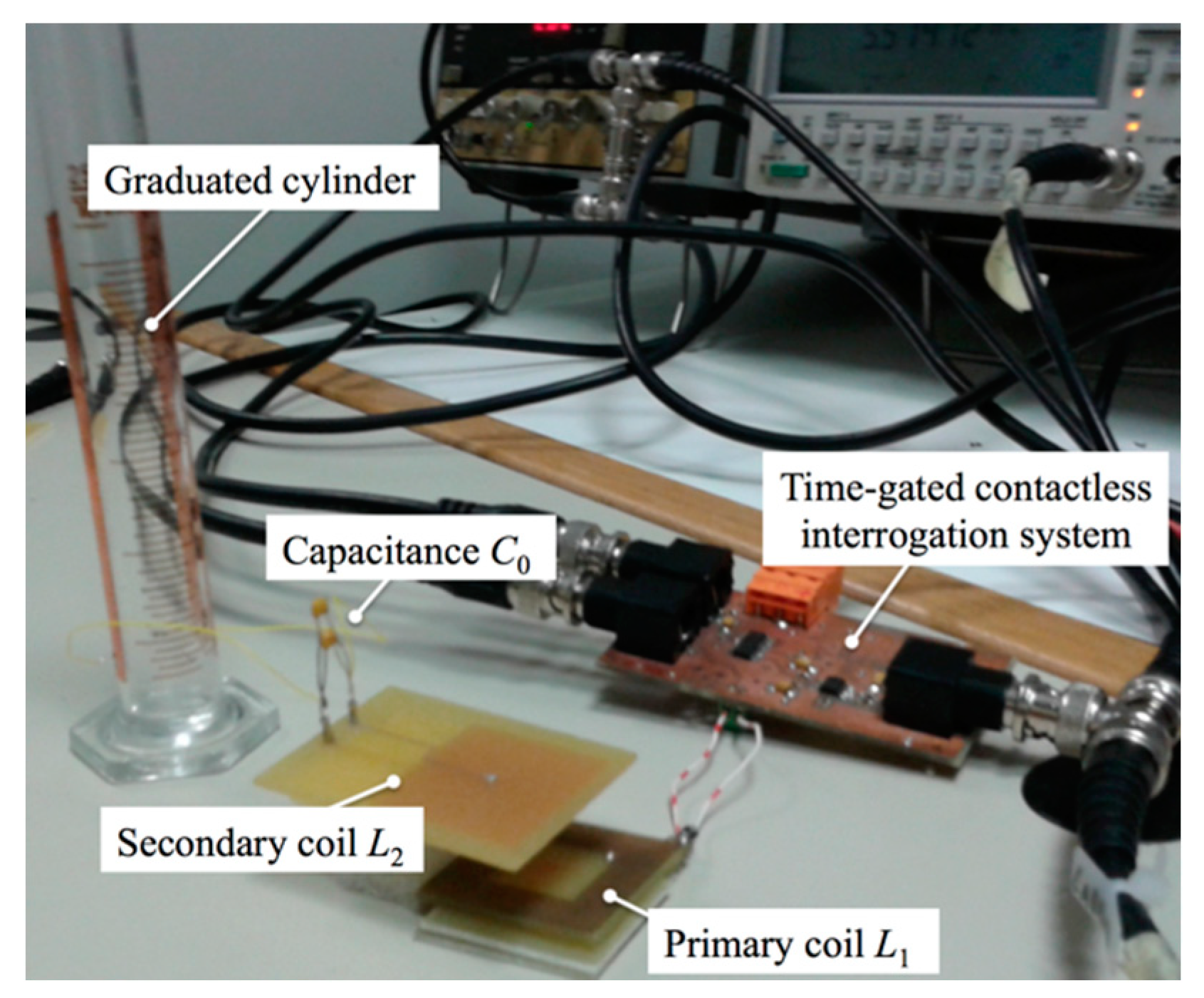
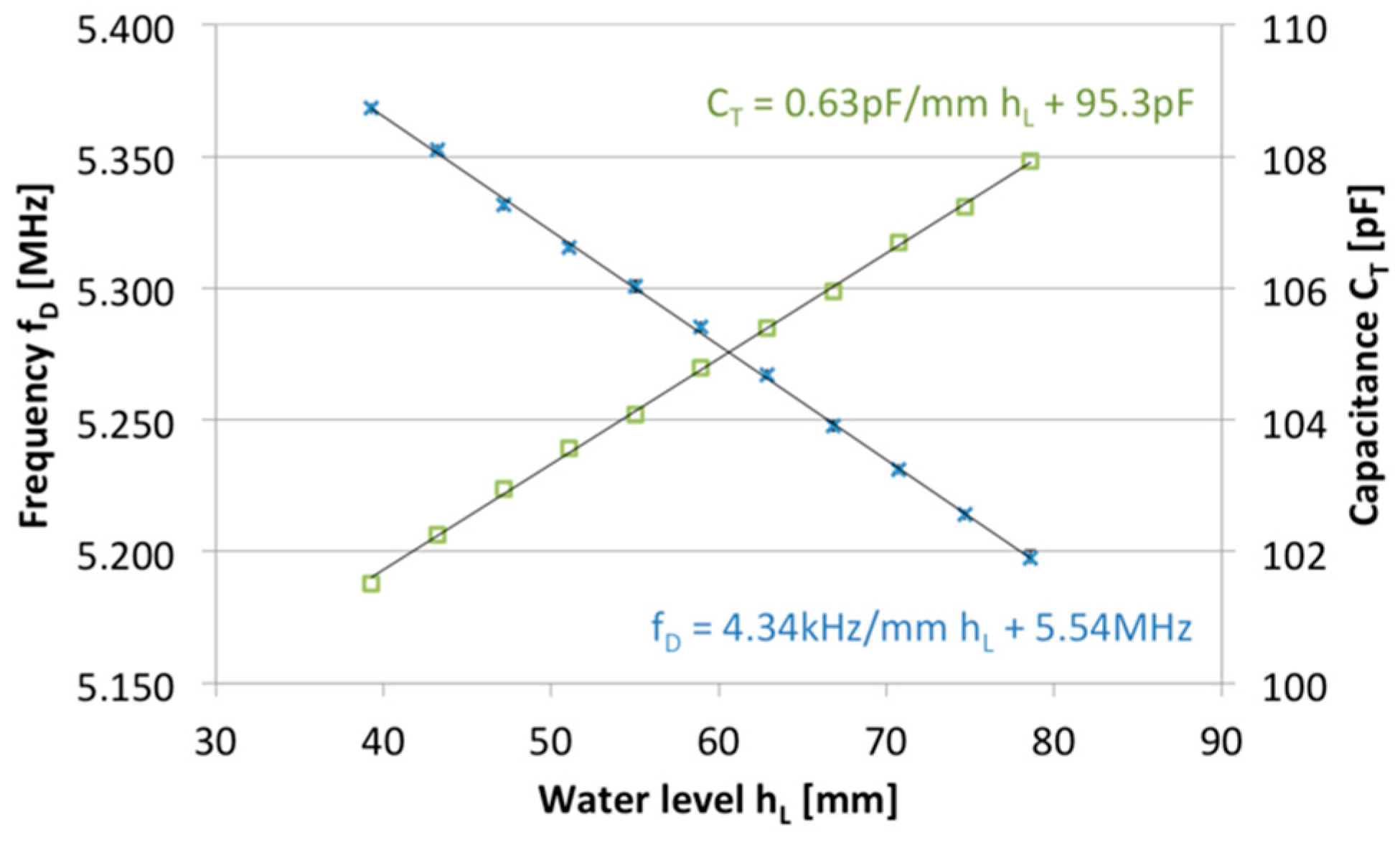
3. Experimental Results
4. Conclusions
Conflicts of Interest
References
- Zhang, C.; Wang, L.F.; Huang, J.Q.; Huang, Q.A. An LC-Type Passive Wireless Humidity Sensor System With Portable Telemetry Unit. J. Microelectromech. Syst. 2015, 24, 575–581. [Google Scholar] [CrossRef]
- Jachowicz, R.S.; Wójtowicz, G.; Weremczuk, J. A non-contact passive electromagnetic transmitter to any capacitive sensor—Design, theory, and model tests. Sens. Actuators A Phys. 2000, 85, 402–408. [Google Scholar] [CrossRef]
- Nopper, R.; Niekrawietz, R.; Reindl, L. Wireless Readout of Passive LC Sensors. IEEE Trans. Instrum. Meas. 2010, 59, 2450–2457. [Google Scholar] [CrossRef]
- Sauer, S.; Marschner, U.; Adolphi, B.; Clasbrummel, B.; Fisher, W.J. Passive Wireless Resonant Galfenol Sensor for Osteosynthesis Plate Bending Measurement. IEEE Sens. J. 2011, 12, 1226–1233. [Google Scholar] [CrossRef]
- Ferrari, M.; Baù, M.; Tonoli, E.; Ferrari, V. Piezoelectric Resonant Sensors with Contactless Interrogation for Mass Sensitive and Acoustic-Load Detection. Sens. Actuators A Phys. 2013, 202, 100–105. [Google Scholar] [CrossRef]
- Baù, M.; Ferrari, M.; Ferrari, V. Analysis and Validation of Contactless Time-Gated Interrogation Technique for Quartz Resonator Sensors. Sensors 2017, 17, 1264. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masud, M.; Baù, M.; Demori, M.; Ferrari, M.; Ferrari, V. Contactless Interrogation System for Capacitive Sensors with Time-Gated Technique. Proceedings 2017, 1, 395. https://doi.org/10.3390/proceedings1040395
Masud M, Baù M, Demori M, Ferrari M, Ferrari V. Contactless Interrogation System for Capacitive Sensors with Time-Gated Technique. Proceedings. 2017; 1(4):395. https://doi.org/10.3390/proceedings1040395
Chicago/Turabian StyleMasud, Mehedi, Marco Baù, Marco Demori, Marco Ferrari, and Vittorio Ferrari. 2017. "Contactless Interrogation System for Capacitive Sensors with Time-Gated Technique" Proceedings 1, no. 4: 395. https://doi.org/10.3390/proceedings1040395
APA StyleMasud, M., Baù, M., Demori, M., Ferrari, M., & Ferrari, V. (2017). Contactless Interrogation System for Capacitive Sensors with Time-Gated Technique. Proceedings, 1(4), 395. https://doi.org/10.3390/proceedings1040395







