Impact of High Coupling Factor in Absolute Distance Measurement with Self-Mixing Interferometry ^†

Abstract

Absolute distance measurement by means of a self-mixing interferometer (SMI) can be obtained by modulating the laser frequency. This modulation is typically achieved through the modulation of the laser injection current with a triangle waveform. Various strategies have been proposed to increase the performances and recent researches have shown real-time performance of SMI with resolution reaching 100 μm for distances up to 2 m. In the present paper, we demonstrate for the first time, both experimentally and by modeling, that with high coupling factors between the laser and the target, disappearance of interferometric fringes occurs that can strongly affect the measurement reliability.

1. Introduction

Self-mixing interferometry has been studied by many research groups in recent years because of its expected lower cost and higher compactness as compared to traditional interferometers, with comparable performances. Sensors under the self-mixing technique use the laser itself as both the light source and the detector. This phenomenon occurs when the light of the laser propagates towards a distant target where it is partially reflected or back-scattered and re-injected into the laser cavity. The back-scattered light interferes with the laser cavity light which creates variations of the threshold gain, the emitted power, and the lasing frequency of the laser. The variation of the laser power is measured with either the monitoring photodiode included in the laser package or through the amplification of the diode voltage itself. Various applications of this phenomenon have already been published such as vibration, absolute distance and velocity measurement [1], and more recently for imaging of acoustic waves [2], micro-scale flow measurement and several biomedical purposes [3].

When the frequency of the laser is modulated in triangle waveform by means of an injection current modulation with a fixed amplitude and frequency, the inner cavity and the back-scattered wave show a phase-shift that is proportional to the target to laser distance. Thus, the interferometric variations of the laser power exhibit periodic fringes which periodicity is proportional to this distance. The most usual method for evaluation of the target distance is by counting the number of peaks that appear on each ramp of the triangle modulation. In this configuration, a simple thresholding on the signal amplitude and a counter is sufficient to perform the distance measurement [3,4]. In this paper, we demonstrate that some fringes disappear when the value of the coupling factor reaches high values. The number of disappeared fringes is proportional to the coupling factor and induces major errors in the measurement.

2. Theory

2.1. Self-Mixing Interferometry Basics

Most of the theoretical modelling on self-mixing is based on the three mirrors model which was initially developed by Petermann [5]. The three mirror cavity is reduced to a two mirrors equivalent cavity where the lasing conditions are established. Thus the laser emission frequency ${\nu }_{}$ is recalculated and compared to the one of the free-running laser ${\nu }_{\mathrm{th}}$,

$$\mathsf{\Delta }{\varphi }_{\mathrm{c}}=2\pi {\tau }_{\mathrm{ext}}\left(\nu -{\nu }_{\mathrm{th}}\right)-C\sin \left(2\pi {\tau }_{\mathrm{ext}}\nu -\arctan \alpha \right),$$

(1)

where ${\tau }_{\mathrm{ext}}=2L_{\mathrm{ext}}/c$ is the round-trip propagation time in the external cavity $L_{\mathrm{ext}}$, and c is the speed of light in vacuum. α is the linewidth enhancement factor of the laser diode and C is the feedback level which describes the strength of the optical feedback changes to the laser behavior. It can be expressed as [6],

$$C=\frac{{\tau }_{\mathrm{ext}}}{{\tau }_{\mathrm{in}}}\epsilon {\kappa }_{\mathrm{ext}}\sqrt{1+{\alpha }^2},$$

(2)

where ${\tau }_{\mathrm{in}}$ is the round-trip delay in the cavity of the solitary laser diode, ε is the fraction of the reflected light coupled back coherently into the lasing mode (normally 0.1 <ε< 0.6), and ${\kappa }_{\mathrm{ext}}$ is the coupling strength between the target and the laser cavity which is expressed as,

$${\kappa }_{\mathrm{ext}}=\frac{r_{\mathrm{ext}}}{r_2}\left(1-{\left|r_2\right|}^2\right),$$

(3)

where $r_{\mathrm{ext}}$ is the ratio of the back-scattered field amplitude and the emitted field amplitude, and $r_2$ is the reflection coefficient of the laser facet. Then the variation of optical power can be expressed as [7],

$$\Delta P=\beta \cos \left({\varphi }_{FB}\right),$$

(4)

where ${\varphi }_{FB}=2\pi {\tau }_{\mathrm{ext}}\nu$, defines the phase response with optical feedback and $\beta$ is the observable signal amplitude that depends on the amount of back-scattered power.

Numerical methods need to be used to solve the laser emission frequency, ${\nu }_{}$, in (1) . A unique solution can be found when the system operates in weak optical feedback (C ≤ 1), and multiple solutions when the laser is operated in moderate and strong optical feedback (C > 1) [8]. In this paper, we are interested in moderate and strong optical feedback where we observe the losses of interferometric fringes [9].

2.2. Absolute Distance Measurement

Absolute distance measurement with the self-mixing technique can be obtained when the laser frequency is modulated with a triangle waveform which is typically achieved by modulating the laser injection current. To model the laser frequency linear dependence on injection current, a characteristic parameter $\mathsf{\Omega }$ is introduced so that [4],

$${\nu }_{\mathrm{th}}\left(I_0+\mathsf{\Delta }I\right)={\nu }_{\mathrm{th}}\left(I_0\right)+\mathsf{\Delta }I\mathsf{\Omega },$$

(5)

where $I_0$ is the bias current and $\Delta I$ is variation of the injection current. However, the linear trend between laser frequency and current is not entirely correct because of several factors such as thermal inertia. With a fixed amplitude and frequency modulation, the output power waveform is a triangle wave with small ripples on the ramps which after filtering of the low frequencies result in a series of sharp peaks. The target distance can be calculated by simply counting the number $N_{\mathrm{f}}$ of these peaks [3,4],

$$L_{ext}=\frac{c{N}_{\mathrm{f}}}{4I_{\mathrm{pk}-\mathrm{pk}}\mathsf{\Omega }},$$

(6)

where $I_{\mathrm{pk}-\mathrm{pk}}$ is the peak-to-peak amplitude of the triangle current modulation waveform is the number of.

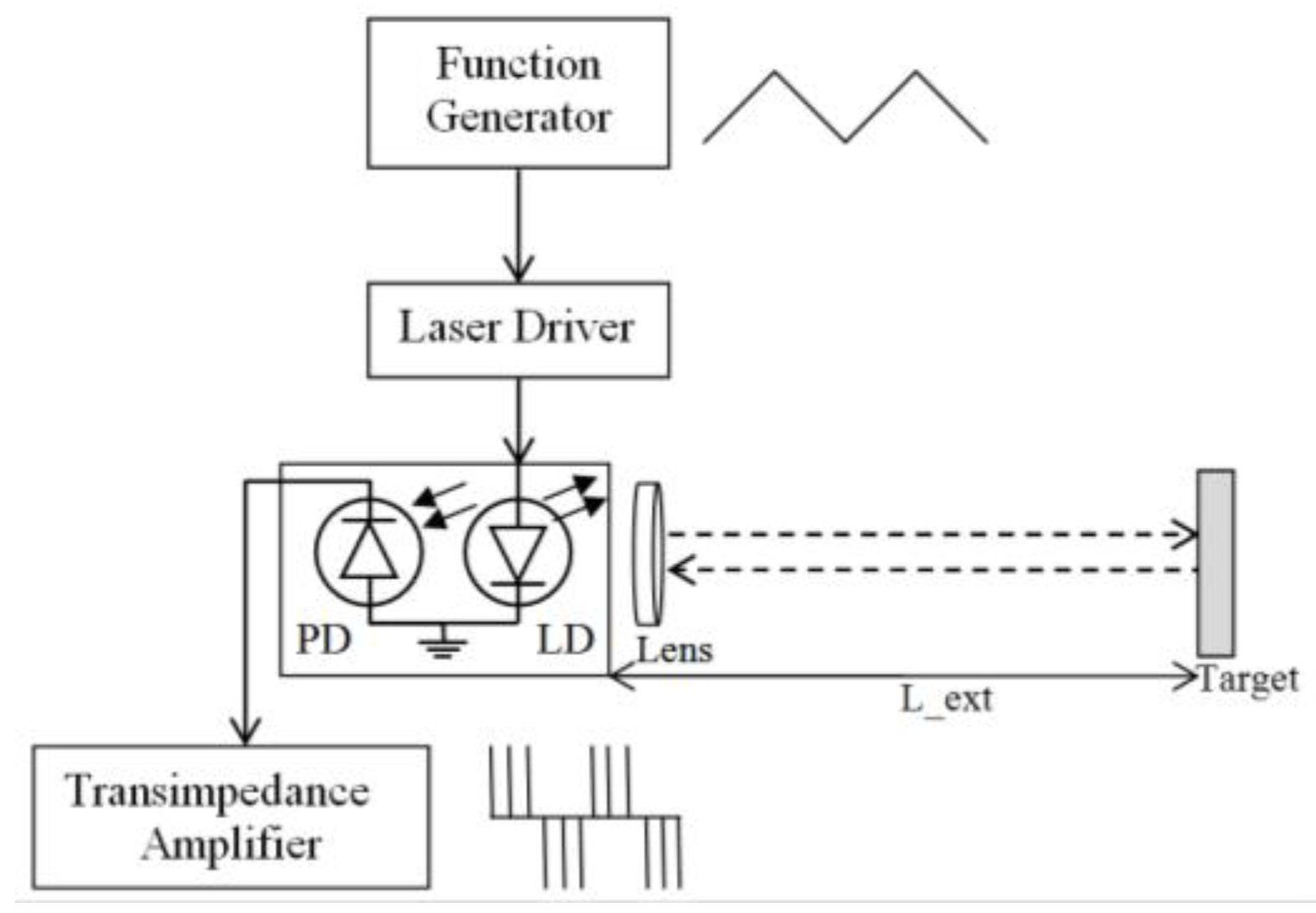
3. Experimental Setup

A block diagram of the experimental setup for absolute distance measurement with SMI is shown in Figure 1. The DFB laser diode (L1550P5DFB, a DFB emitting at 1550 nm) with a package included monitoring photodiode was associated to a lens which focuses the laser beam onto the target surface. The target is a flat metallic surface partially covered by a microspheres reflective tape. The laser was operated with a bias current of 20 mA and modulated with a 10 mA peak-to-peak amplitude triangular waveform. The photodetected signal is converted to voltage by a transimpedance amplifier.

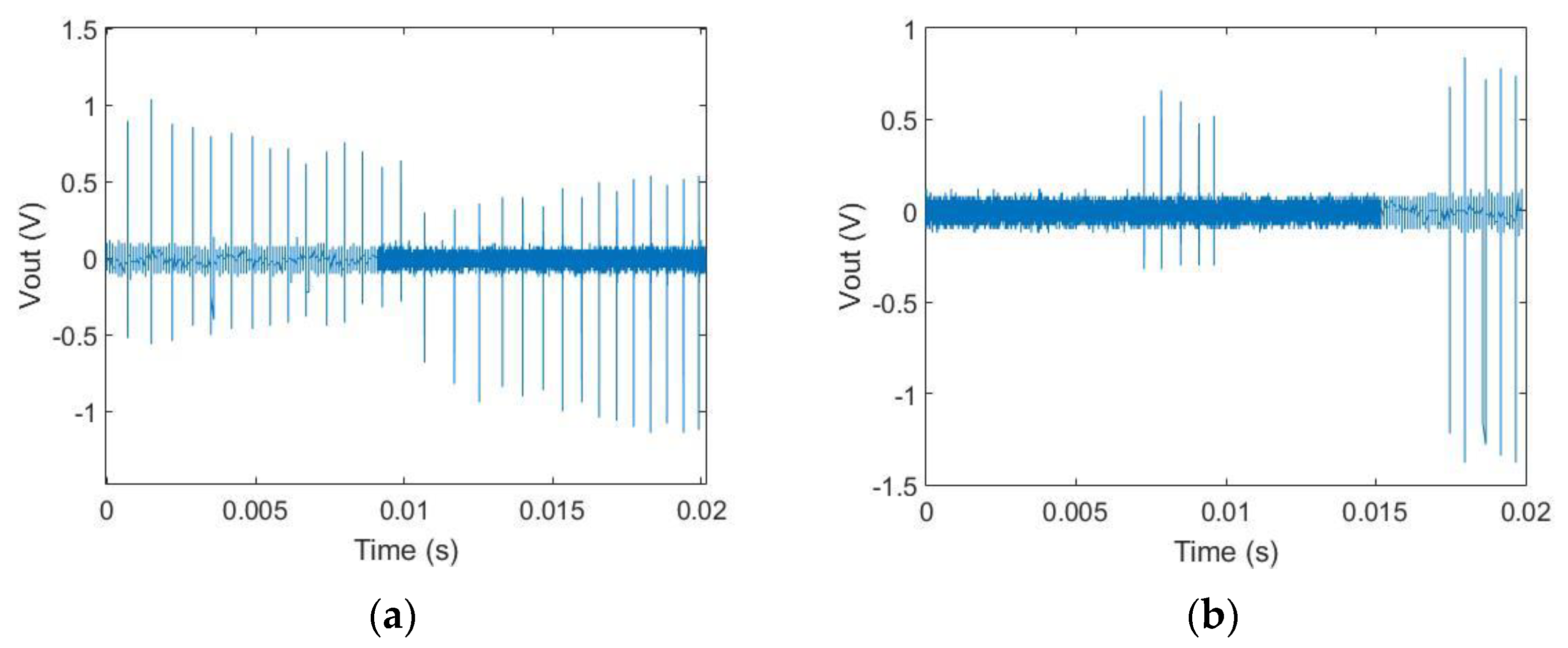
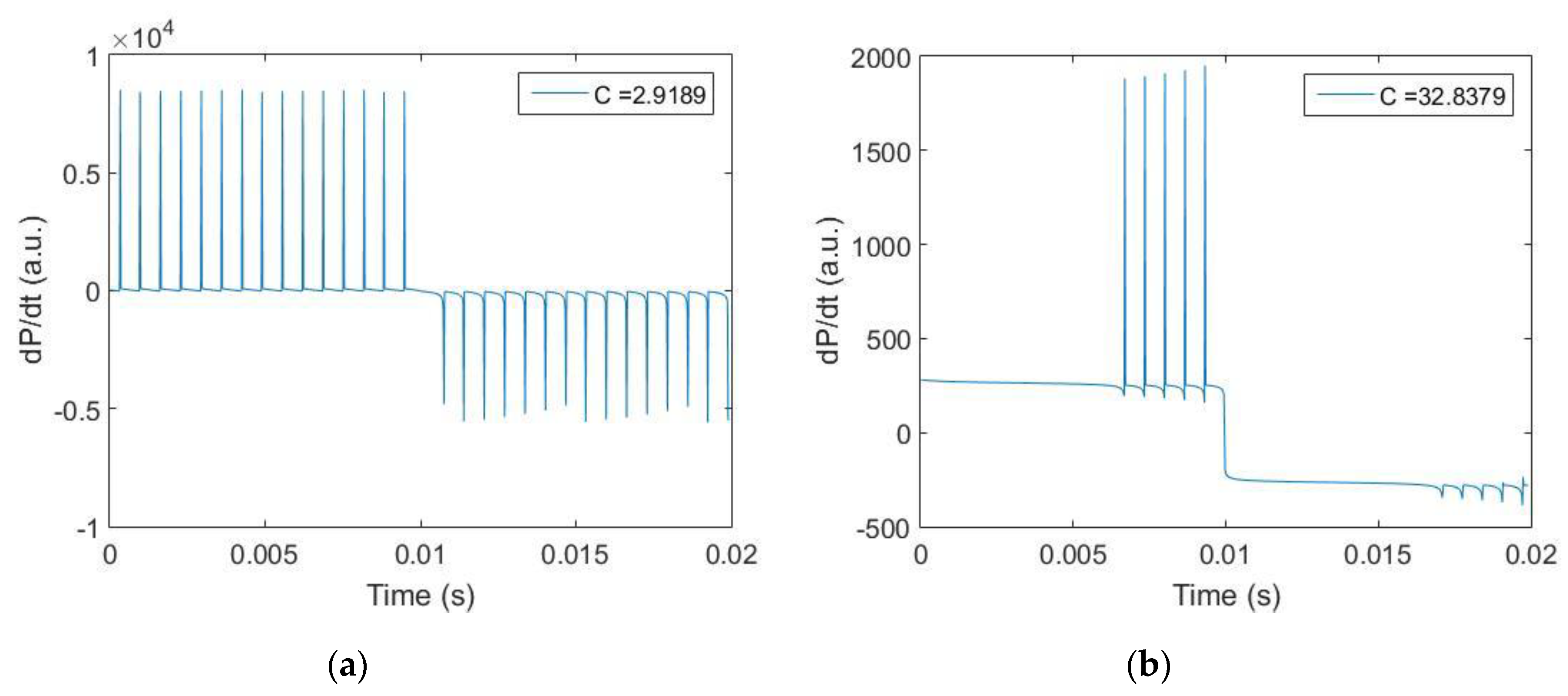
4. Results

Two parameters were measured experimentally: the frequency modulation coefficient $\mathsf{\Omega }$ and the reflectivity coefficient $r_{\mathrm{ext}}$. The coefficient $\mathsf{\Omega }$ is function of many parameters (frequency modulation, feedback level, temperature, modulation frequency, etc). For this experiment, we chose a set of conditions which resulted to a FM coefficient of −380 MHz/mA. The reflectivity coefficient $r_{\mathrm{ext}}$ of the target is one of the most important parameter to the feedback strength C. For a distance of 60 cm, we measured it at 5.2 × 10⁻³ with the metallic surface and 58.5 × 10⁻³ with the microspheres reflective tape. Figure 2 shows the signals obtained for one period of modulation by a triangle signal. While the metallic surface produces a signal with regular periodic fringes, with the microspheres reflective tape, number of fringes have disappeared even if the frequency of the remaining fringes is similar to the one observed with metal. Figure 3 shows the result of the simulation by applying the measured parameters which matched to the experimental results. As can be seen on Figure 3, the simulation of the sensor signal using the set of Equations (1)–(4) provides with a very resembling pattern to the measured one. Moreover, the values of coupling coefficient C that fits the best to obtain this resemblance is multiplied by exactly the same amount as the measured reflectivity $r_{\mathrm{ext}}$, thus validating the modeling approach.

5. Conclusions

The paper proposes a model based and experimental study of high coupling factors impact in absolute distance measurement using the self-mixing interferometry scheme. It is demonstrated for the first time in such measurement that interferometric fringes may disappear. Missing fringes can strongly affect the distance measurement resolution. Further analysis of this phenomenon shall target a clearer understanding of the fringes disappearance process and quantification, in order to propose a better suited absolute distance calculation method.