Metasurface-Based THz Dual-Band Absorber Sensor for the Measurement of Refractive Index Variations of Chemical and Biological Substances ^†

Abstract

In this paper we report on the results of the simulations of the electromagnetic properties of a metasurface composed of a 2D-array of plasmonic nanoantennas acting as polarisation insensitive dual band THz perfect absorber able to achieve absorption coefficients and quality factors up to 99.6% and 122, respectively. The 2D-array is designed on top of a polyimide flexible film separating it from an Ag ground layer. The plasmonic nanoantenna is composed of two Ag quadrangular rings and an Ag diamond-shape dot is placed at their geometrical centre. The absorption resonances show a linear frequency shift with respect to variations of the refractive index of transparent substances adsorbed on the metasurface. This allows the dual-band absorber to be employed as a sensor of the chemical/physical modifications taking place on the substance. In particular, in terms of the refractive index units, the sensor based on the dual-band absorber can achieve sensitivities up to 310 GHz/RIU.

1. Introduction

The study of the electromagnetic (e.m.) properties of MetaSurfaces (MS) used to implement perfect THz absorbers is attracting great attention for their potential applications as imagers and high-sensitive detectors as well as chemical, drug and explosive substance sensors [1,2,3]. In general, MS are 2D-arrays of ordered metal sub-wavelength NanoAntennas (NA) grown on dielectric, semiconductor and/or flexible plastic substrates. The NA shapes, sizes and mutual distances determine the MS spectral behaviour in terms of frequency and polarisation dependent reflection and transmission responses [4]. In particular, for the performance optimisation of the perfect THz absorbers used as sensing devices, it is necessary to study NA geometries and 2D-array structures with an e.m. response insensitive to the polarisation of the incident radiation and characterised by narrow spectral bandwidth, high quality factors (Q-factors) and absorption coefficients approaching 100% [5,6]. In this regard, the main difficulty for the enhancement of the MS-based device sensitivity and resolution is the relatively low value of the achieved Q-factors that limits the detection of extremely small MS resonance frequency shifts occurring in presence of substances close-to or adsorbed-on the MS. To date, the maximum reported Q-factors for a perfect dual-band absorber in the THz region is equal to 59.8 achieved by using a simple metal rod shape for the NA with a maximum absorption coefficient of 99.6% [6]. However, the e.m. properties of this particular MS are intrinsically polarisation dependent. On the other hand, the polarisation independent version makes use of cross-shaped NA for which a Q-factor equal to 48.8 has been achieved with a maximum absorption coefficient equal to 85.3% [6]. Moreover, for the dual-band perfect absorber configurations it is observed great changes of the Q-factors of the two absorption resonances. In the case of the results reported in [6], for example, the Q-factors of the absorption resonances occurring at the higher frequency are 8.4 and 7.7, smaller than those ones related to the lower frequency absorption resonance for the rod- and cross-shaped NA, respectively. As a consequence, only one of the two absorption resonances of the dual-band perfect absorbers (i.e., that one with the highest Q-factor) can be properly used to probe the presence of a substance (i.e., an analyte) adsorbed on its surface. In this paper, we present a novel THz dual-band perfect absorber that overcomes this problem allowing to reach Q-factors higher than 100 for both the two absorption resonances.

2. Design, Results and Discussion

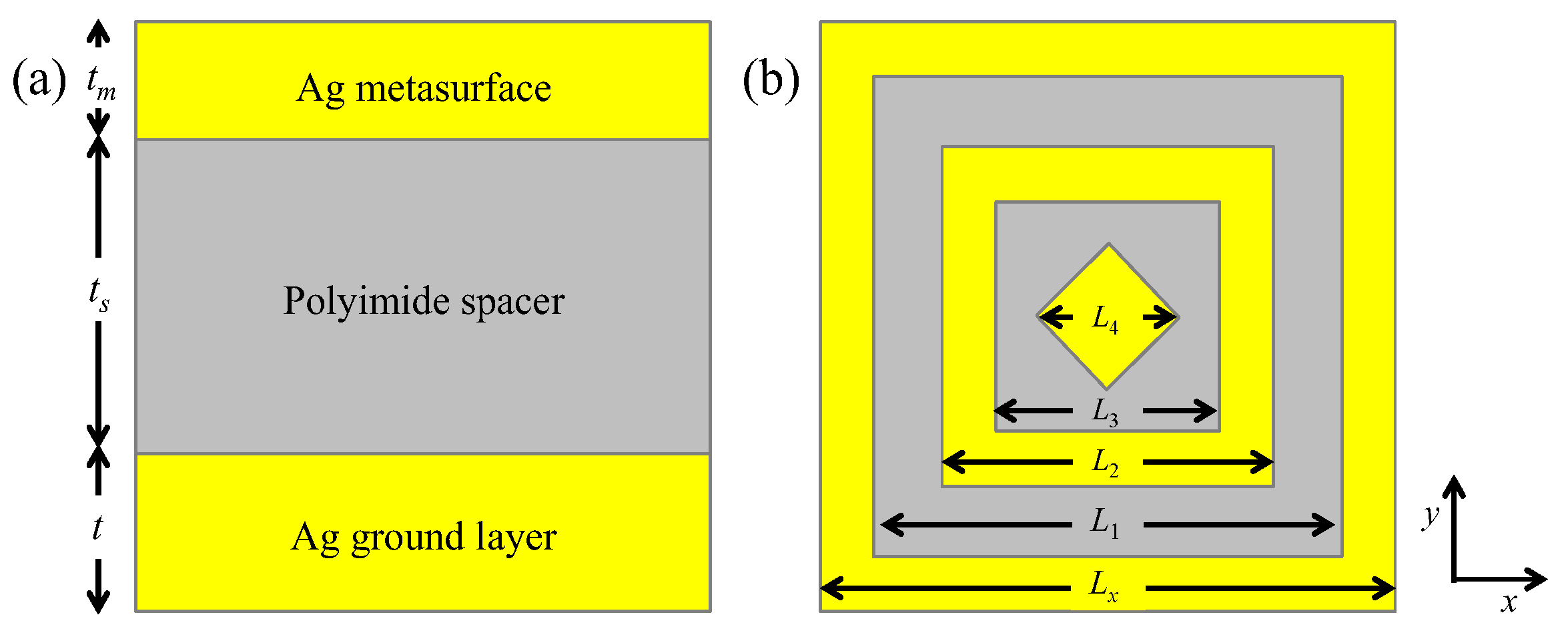
In Figure 1 is reported the cross section (panel a) and the plane view (panel b) of the proposed dual-band perfect absorber. The cross section shows that the MS 2D-array of Ag NA is located on top of a polyimide flexible film that separates the MS from the Ag ground layer. Here t_m, t_s and t are the Ag MS, polyimide spacer and Ag ground layer thicknesses, respectively. The use of the polyimide film allows fabricating the MS by using, for instance, the electro-hydrodynamic jet printing technique [7]. Referring now to the plane view reported in panel (b) of Figure 1, the NA geometry is composed of two concentric Ag square rings and of an Ag diamond-shape dot located at their centre. In the same figure, the lengths L_x, L₁, L₂ and L₃ are the outer and inner sides of the outer and inner square rings, respectively, and L₄ is the diagonal of the diamond-shape dot. Note that L_x represents also the lattice parameter of the 2D-array MS.

The e.m. response of the designed MS has been investigated by using FEM analysis in the frequency domain. The simulations were performed illuminating the MS by using a TM and TE linear polarised e.m. plane wave propagating along the z-direction perpendicular to the MS (x,y) plane (see Figure 1). Starting from the unit cell reported in Figure 1, the MS 2D-array was obtained by using periodic boundary conditions along the x- and y-directions and scattering boundary conditions along the z-direction. Under these conditions, the symmetry properties of the NA shape allow the e.m. response of MS to be independent from the polarisation of the incident radiation. For the numerical simulations the following values of the dual-band perfect absorber geometrical parameters have been used: L_x = 100 μm, L₁ = 85 μm, L₂ = 70 μm, L₃ = 50 μm, L₄ = 21.3 μm, t_m = 0.2 μm, t_s = 8 μm, t = 0.4 μm. Moreover, the Ag relative electric permittivity has been calculated through the Drude model using the plasma frequency ω_p = 1.4 × 10¹⁶ rad/s and the damping coefficient Γ_Ag = 0.32 × 10¹⁴ s⁻¹. The polyimide dielectric permittivity equal to (3.6 + 0.005i) is assumed constant within the frequency range chosen for the simulations. Since the MS transmission is eliminated, due to the presence of the Ag ground plane in the unit cell which is much thicker than the Ag penetration depth in the THz spectrum range, the MS absorption response can be calculated by using the relation A(ω) = 1 − R(ω), where A(ω) and R(ω) are the frequency dependent absorption and reflection coefficients, respectively.

In panel (a) of Figure 2 is reported the spectral response of the dual-band perfect absorber for the TM polarisation mode showing two resonances centred at f₁ = 1.80 THz and f₂ = 2.27 THz both having maximum absorption coefficients and Q-factors equal to A(f₁) = A(f₂) = 99.6% and Q(f₁) = 122 and Q(f₂) = 96, respectively. Identical results have been obtained for the TE polarisation mode. The values of the Q-factors indicate that the designed dual-band absorber accomplishes a strong frequency selectivity for both the frequencies f₁ and f₂ demonstrating an overall improvement more than a factor 2 with respect to the best results reported in literature [6,8,9,10]. In order to explain the physical origins of the two resonances of the dual-band absorber, in panel (b) of Figure 2 are reported its spectral response under the following conditions: (i) if the NA inner square ring is absent, only the resonance centred at f₁ is present (continuous black line) with Q’(f₁) = 121 and A’(f₁) = 58%; (ii) if the outer NA square ring is removed, only the resonance at f₂ is observed (red dotted line) with Q’(f₂) = 106 and A’(f₂) = 98%, thus similar to the corresponding one shown in panel (a) of Figure 1 These results demonstrate that the Q-factors are not affected by the absence of one of the two NA rings and that the resonance at the frequency 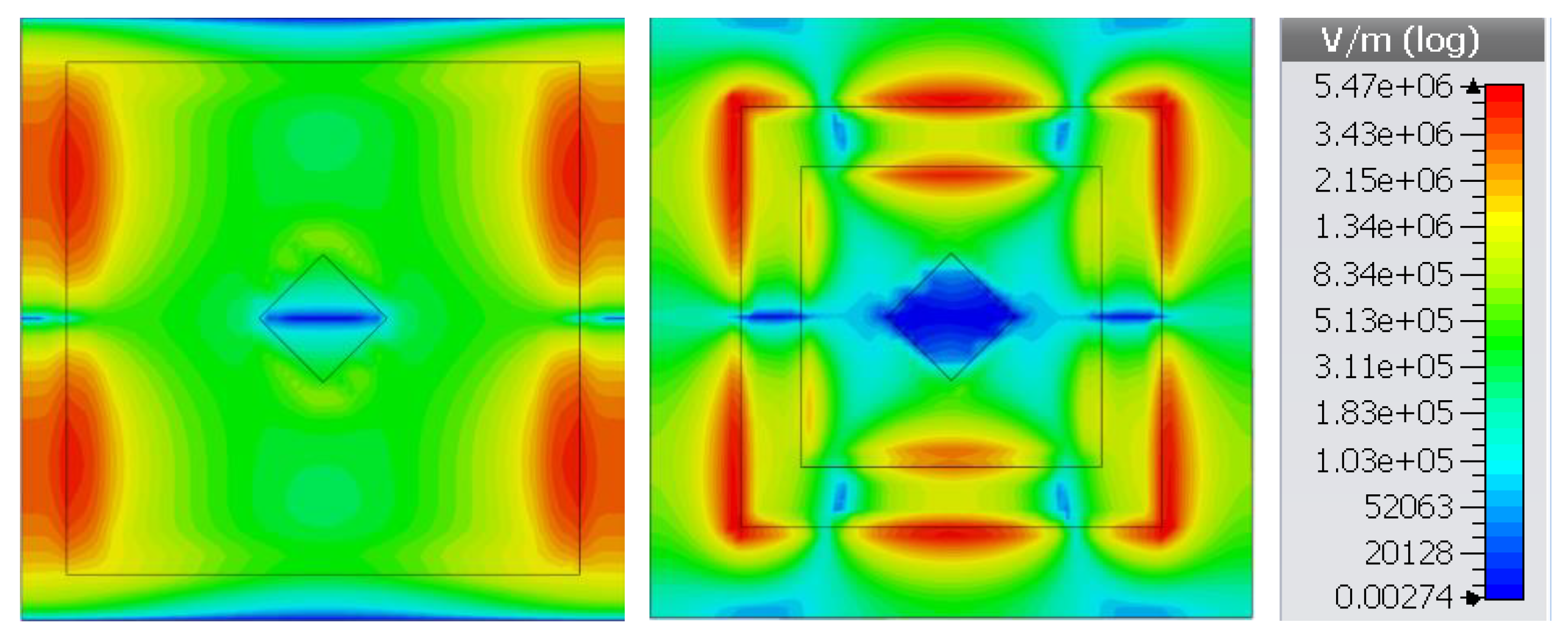f₁ is strongly enhanced through the e.m. interactions arising in the region between the two NA square rings. In order to prove this, in Figure 3 we report the distributions of the intensity of the electric field just above the MS calculated at the two frequencies f₁ and f₂.

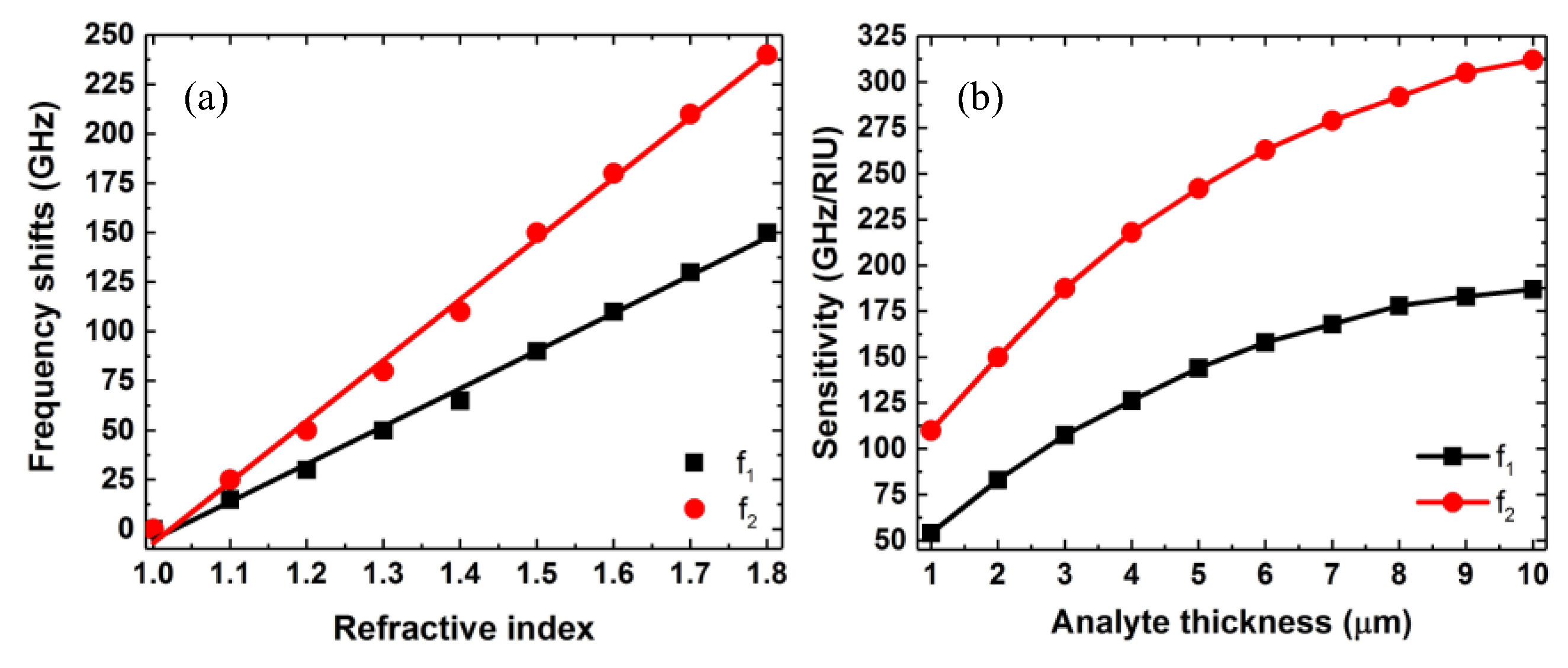
The interesting e.m. properties of the proposed dual-band absorber suggested to use it as a sensor to measure the changes of the refractive index of a transparent analyte adsorbed on top of the MS. In panel (a) of Figure 4 we report the dependence of the frequency resonances f₁ and f₂ on the variation of the analyte refractive index. The linear dependence allows defining the sensitivity of the sensor based on the dual-band absorber that, in terms of the Refractive Index Unit (RIU), reaches values up to σ(f₁) = 180 GHz/RIU and σ(f₂) = 310 GHz/RIU for the resonance frequencies f₁ and f₂, respectively (see panel (b) of Figure 4). Finally, the plot in panel (b) of Figure 4 shows that the sensitivity depends on the analyte thickness opening the possibility to use the designed dual-band absorber to measure also the amount of analyte adsorbed on the MS.

3. Conclusions

In this paper we reported on the electromagnetic response of a novel polarisation insensitive dual-band perfect absorber composed of a 2D-array of plasmonic nanoantennas able to achieve absorption coefficients and quality factors up to 99.6% and 122, respectively. With respect to the previous results reported in the literature, the proposed metasurface geometry allows having the same properties in terms of absorption coefficient and quality factor for both the two absorption resonances. This permits to employ the dual-band absorber as a sensor of chemical/physical modifications of analyte adsorbed on the metasurface. In particular, in terms of the refractive index units, the sensor based on the dual-band absorber can achieve sensitivities up to 310 GHz/RIU.