A Comb-Based Capacitive MEMS Microphone with High Signal-to-Noise Ratio: Modeling and Noise-Level Analysis ^†

Abstract

We present a physics-based system-level model for optimizing a novel comb-based capacitive MEMS microphone towards high signal-to-noise ratios. The model includes non-linear coupling effects between the electrodes as well as the physical dependencies on relevant design parameters, thus enabling predictive statements w.r.t. the device performance. It is calibrated and validated by finite element simulations and laser Doppler vibrometer measurements of first prototypes. Being formulated as a generalized Kirchhoffian network, it can be implemented in a standard circuit simulation tool. The predicted signal-to-noise ratio of this concept reaches up to 78 dB(A), which significantly exceeds state-of-the-art devices.

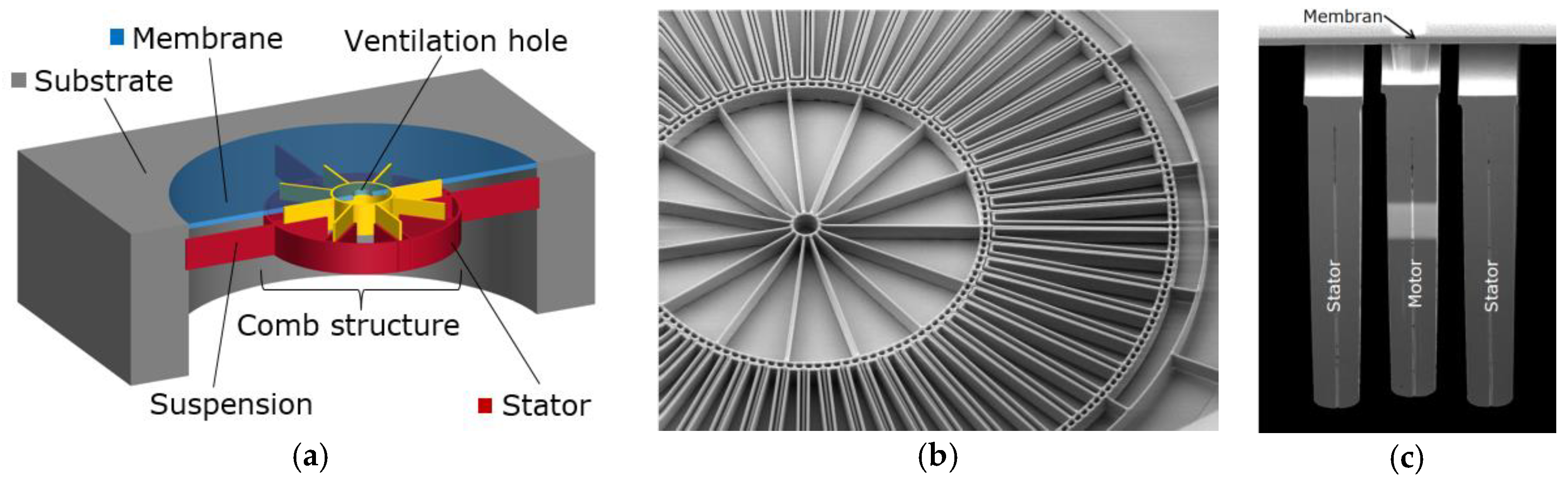
1. Motivation and Description of Device Concept

Conventional backplate-based silicon microphones have reached a mature state in the market, especially in mobile communication applications. Consisting of a moveable membrane, which detects incident acoustical waves by the capacitance change w.r.t. a stiff, perforated backplate [1], they suffer from high fluidic noise, which limits the signal-to-noise-ratio (SNR) achievable by this technology. In order to overcome this constraint, a novel microphone concept was recently introduced in [2]. Thereby radially aligned comb fingers are attached to the bottom side of a moveable membrane (see Figure 1).

In conjunction with a spidernet-like stator fixed to the substrate underneath, they form an interdigitated comb-system. This specific design as a backplate-free device is expected to exhibit lower losses and, thus, higher SNR compared to classical microphones.

First system-level models of this design are presented in [2,3], describing the microphone as a system of two coupled one-dimensional harmonic oscillators. Membrane and stator are both considered moveable and couple via electrostatic and fluidic damping forces. However, up to now, only linearized operation around a fixed working point (e.g., fixed fluidic damping coefficient taken from FE-simulation) could be simulated. In this work, the model is extended to a generalized, physics-based description including the dependencies on the relevant design parameters for all involved coupling mechanisms, thus building the basis for predictive simulation and optimization with respect to the key figures “noise” and “SNR.”

2. Physics-Based Modeling of Electrostatic Force and Fluidic Damping

The microphone model is intended for system-level simulation covering the interplay of the transducer, package and read-out electronics. Hence, the model complexity for each subsystem has to be reduced. For the comb read-out, periodic boundary conditions are applied and only the two-dimensional cut as shown in Figure 2a and Figure 3a is considered for deriving the electrostatic and fluidic subdomain models. Subsequently the 2D models are extruded to model the full 3D operation.

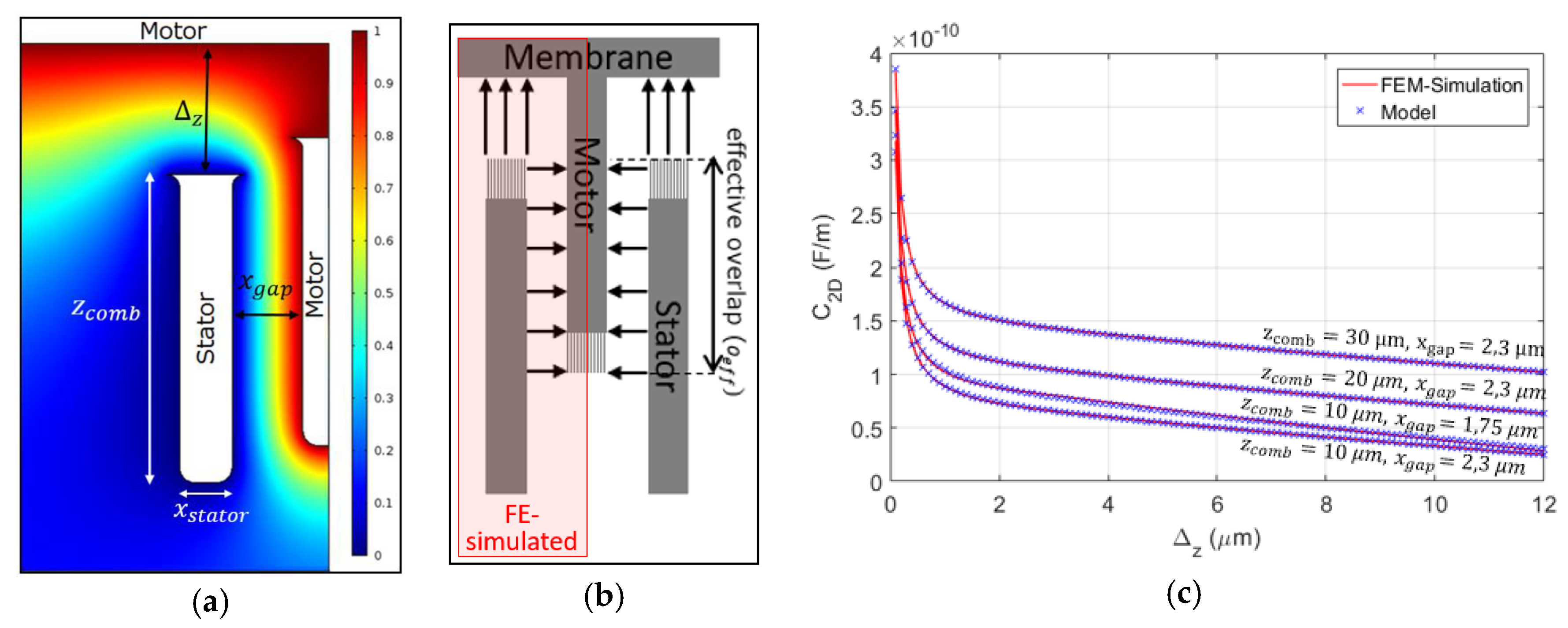
2.1. Capacitive Transducer Model

The capacitive transducer model is built by summing up the electric capacitance between membrane and stator ($C_{plate}$) and the electric capacitance between the comb fingers ($C_{comb}$), both depending on the vertical displacement ${\Delta }_z$:

$$C_{2D}=C_{comb}+C_{plate}={ϵ}_0\frac{x_{stator}}{{\Delta }_z}+{ϵ}_0\frac{z_{comb}+z_{FE}-{\Delta }_z }{x_{gap}}$$

(1)

Here,${ϵ}_0$ is the permittivity, $x_{stator}$ the lateral width of the stator comb, and $x_{gap}$ the lateral distance between motor and stator combs. Fringing fields are taken into account introducing an effective overlap of the combs $o_{eff}=z_{comb}+z_{FE}-{\Delta }_z$, where $z_{FE}$ is extracted from finite element simulation (FE). The total active capacitance of the microphone is obtained by multiplying Equation (1) with the number of comb-systems (N), the radial length of combs (L) and a factor of 2 for symmetry reasons. Figure 2c shows that the resulting model exhibits an accuracy of above 95% for parameter variations within the relevant design space.

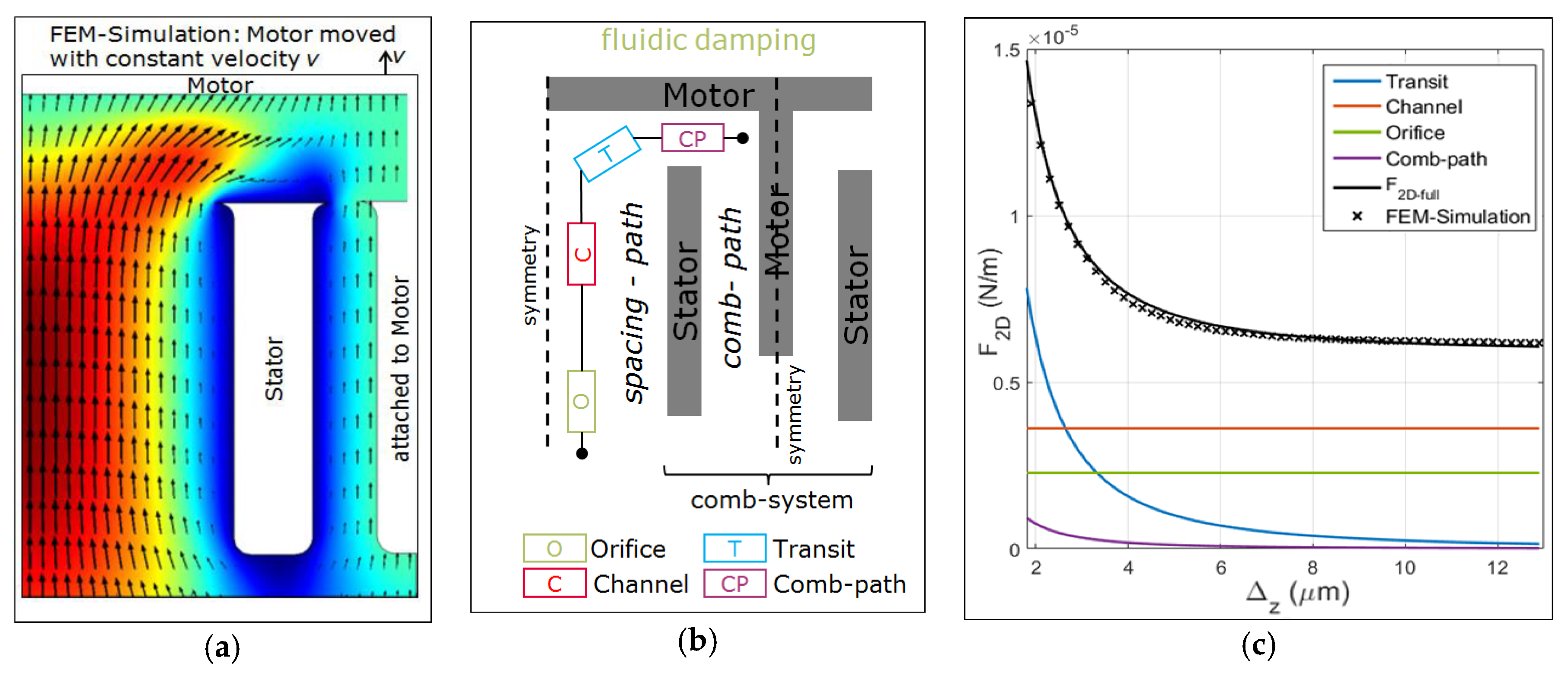
2.2. Fluidic Damping Model

Fluidic FE simulations have been carried out in order to identify the most dominant contributions to the fluidic damping. The air flow in the symmetric basic cell of the comb structure is depicted in Figure 3a. It is dominated by the broader channel between two neighboring comb systems (“spacing path”), allowing to neglect the slide-film damping effects in the “comb-path”. The contributions to the damping can be modeled applying a fluidic network consisting of a Hagen-Poiseuille flow in the channel $Z_C$, a viscous orifice flow $Z_O$, and a transit region represented by $Z_T$. Analytical formulations for the network components can be derived from the Stokes equation and e.g., be found in [4]. Using a correction structurally similar to $Z_T$ to take into account the residual flow through the “comb-path” $Z_{CP}$, the fluidic damping model can be formulated as:

$$Z_{fluid,2D}=Z_T+Z_C+Z_O+Z_{CP}=\frac{3\pi \eta }{{\Delta }_z^2}\tau +\frac{12\eta z_{comb}}{x_{channel}^3}+\frac{3\pi \eta }{x_{channel}^2}+\frac{p_{FE} z_{comb}}{{\Delta }_z^2}$$

(2)

Here, $\eta$ is the viscosity of air and $x_{channel}$ the mean distance of two neighboring comb cells. The correction factor $p_{FE}$ is extracted from FE-Simulation. The resulting damping forces obtained by Equation (2) show an overall precision of 97% compared to FE-Simulations (see Figure 3c). Finally, the total damping force is obtained by extruding this model in radial direction and multiplying Equation (2) by the number of comb-systems and a factor of 2 for symmetry reasons.

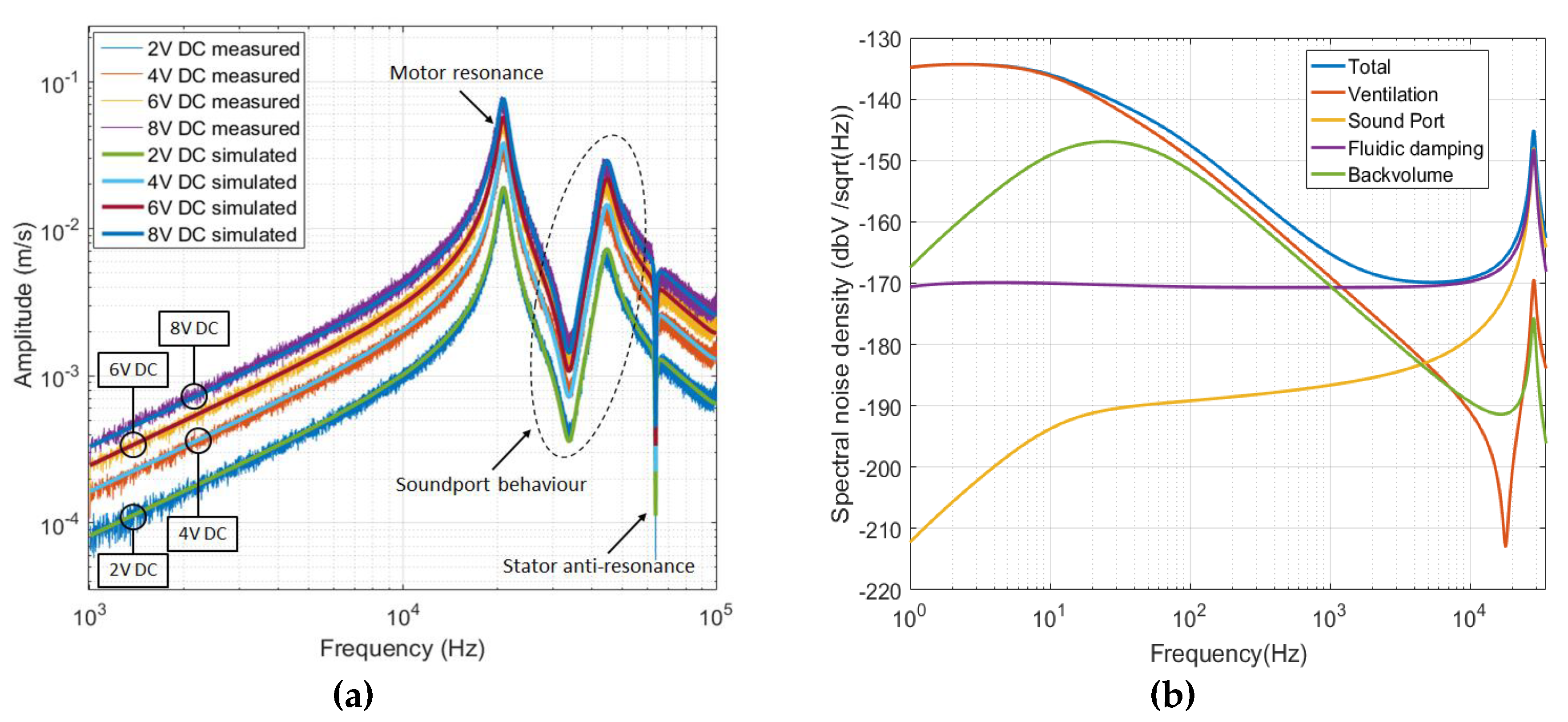
2.3. Verification of the System-Level Model

In order to validate the above described models, they are implemented into a system-level model derived in [2], allowing for comparison of the membrane frequency response to data recorded by laser Doppler (LDV) vibrometry of first prototypes. The simulations reproduce the amplitude as well as the resonance frequencies and their peak widths (which is equivalent to the Q factor) for varying bias voltages with excellent agreement (Figure 4a). This proves the quality of the derived submodels as well as the quality of total system-level model including the couplings between the single energy domains. Comparison of measured and simulated amplitudes and Q factors for different design variants are listed in

Table 1. Simulated and measured Q-factors and displacements for different design variants (N: number of comb-systems, L: radial width of comb-fingers).

Parameter	Q-Factor (sim.)	Q-Factor (meas.)	Amplitude at 1 kHz (sim.)	Amplitude at 1 kHz (meas.)
N = 60, L = 150 μm	10.0	$9.91$ ± 0.04	40.8 nm	$39.5$ ± 0.3 nm
N = 30, L = 150 μm	14.6	$13.7$ ± 0.50	26.1 nm	$26.3$ ± 4.5 nm
N = 90, L = 200 μm	7.69	$7.39$ ± 0.08	58.9 nm	$61.0$ ± 0.2 nm

. The accuracy of over 94% for all design variants validates the 3D extrusion of the subdomain models and demonstrates the predictive power of the system model.

3. Noise and SNR

The validated, physics-based system-level model can now be applied to optimize the device concept w.r.t. its total SNR. In order to get the highest dynamic range and a linear sensor response, an overlap of the combs of 50% is suggested, which has not been technologically realized yet. Figure 4b shows the simulated spectral noise density and discriminates the contributions of different parts of the device to the overall noise level, considering a fully packaged microphone as described in [2]. It revealed that the proposed variant yields very promising SNR values of up to 78 dB(A), which is exceeding state-of-the art microphones. The simulated sensitivity of the microphone amounts to −45.2 $\frac{\mathrm{dBV}}{\mathrm{Pa}}$. Although the noise contribution of the ASIC is neglected here, the results indicate the potential and the promising perspective of the device for further investigations.

4. Conclusions

We presented a physics-based and hence predictive system-level model describing the electrode coupling in comb-based capacitive MEMS-microphones designed for high SNR. All subdomain models are validated by FE-simulations and measurements. The system model is applied to investigate the potential of the device w.r.t. the obtainable SNR. Simulations of a design variant with 50% overlap of the comb fingers reveal a very promising SNR of 78 dB(A) and provide the design space for the technological realization of optimized devices.