Direct Piezoelectric Coefficient Measurements of PVDF and PLLA under Controlled Strain and Stress ^†

Abstract

Open-circuit direct piezoelectric coefficients g₃₁ of bi-axially stretched PVDF and chiral PLLA are reported. This measure is decisive for sensor, generator and energy harvesting applications. We use an in-situ method with contactless voltage measurement during a conventional tensile-test, greatly improving measurement precision (error less than 10%).

1. Introduction

Polymers such as poly(vinylide fluoride) (PVDF) have piezoelectric and pyroelectric properties due to their ferroelectric intrinsic chemical formulation and after being subjected to high voltage electrical poling. Other polymers such as Poly-lactic acid (PLA) do not need electrical poling. They develop natural piezoelectricity after mechanical stretching. For the PLA, the stretching creates a non-chiral film poly-l-lactic acid (PLLA) presenting only one shear piezoelectric constant d₁₄ between 10 × 10⁻¹² C.N⁻¹ [1] and 18.9 × 10⁻¹² C.N⁻¹ [2]. This biodegradable polymer presents the advantage of not being pyroelectric, ensuring an absence of drift with the temperature.

To evaluate piezoelectric coefficients, methods such as laser interferometry, low-frequency surface acoustic waves, bimorph bending, or piezo-response force microscopy, are usually used to determine the piezoelectric strength constant d₃₁, determinant for the actuation. In contrast, for sensors, generators and energy harvesting voltage, performances rely on g₃₁ which usually is simply estimated from d₃₁ measurements and almost never measured directly with polymers. This leads to high uncertainty and imprecision (≥30%).

In this work, we consider a new approach [3] to measure directly the g₃₁ coefficient with great reliability (error under 10%). This method, coupled with dielectric constant measurement of the material, allows the determination of the d₃₁ coefficient, which is the one mainly used to express the piezoelectric performance of materials. Measurements have been performed on an experimental PLLA film from TOTAL and a commercial biaxially stretched PVDF film from PIEZOTECH.

2. Experiments

2.1. Sample Preparation

In this study, the PLLA film was obtained from 250 μm thick cast PLA material followed by controlled stretching (5 times) with a tensile test machine at a temperature above the Tg (100 °C). A 100 μm thick monoaxially stretched PLLA film is achieved.

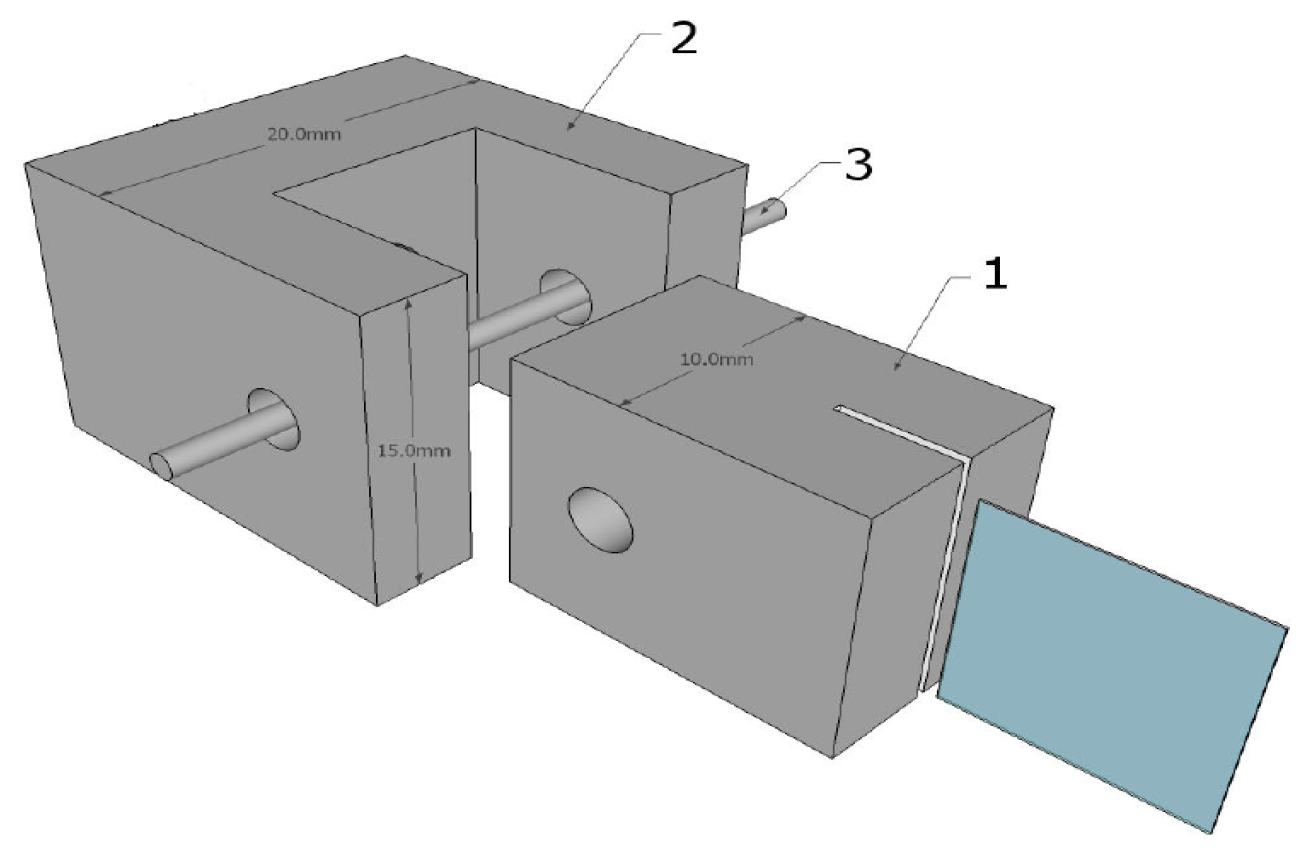
Taking into account the geometric specifications described in [3], samples for our tests are then cut in the 100 μm PLLA film and the 40 μm commercial PVDF film with a length to width ratio upper than 8. The cut samples are then glued with cyanoacrylate glue into 3D-printed clamps and dried for 24 h as shown in Figure 1. The clamps are used to mount the polymer samples into the tensile-test apparatus (MTS) while allowing for in-situ measurements on the samples during stretching. The “active” area between the two clamps has a length of 80 mm and a width of 10 mm.

Silver conductive grease (CW7100 from CIRCUITWORKS) is subsequently used as electrode material on the active area on both side of the samples. Measurements up to 10% of strain can be performed without electrode damage. Contact with the grease for measurements is insured with thin wires attached to the 3D clamps.

2.2. g₃₁ Determination

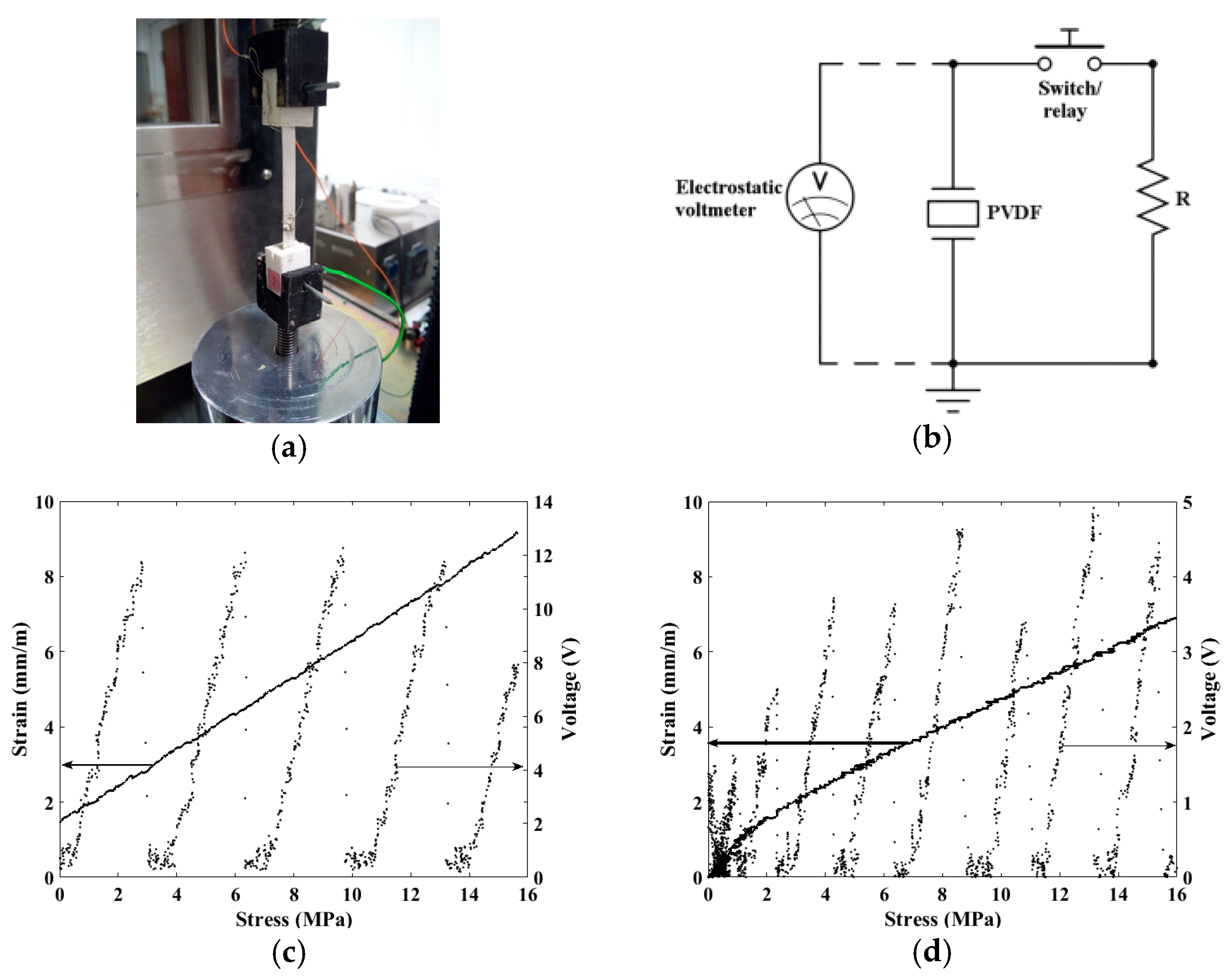
In order to extract the piezoelectric coefficient, the tensile test machine is used to strain the film as shown in the Figure 2a. First of all, the force F is registered with a force sensor and the resulting stress σ is determined using sample dimensions: thickness t and width w (1). The strain S is obtained by dividing the direct measurement of the tensile machine’s displacement over the initial sample length. From this measurement, the compliance c₃₁ over a direction is calculated (2).

$$\mathsf{\sigma }=\frac{\mathrm{F}}{\mathrm{w}.\mathrm{t}},$$

(1)

$$\mathsf{\sigma }={\mathrm{c}}_{31}.\mathrm{S}$$

(2)

During a tensile cycle, the piezoelectric coefficient g₃₁ is calculated. The method consists in measuring the open-circuit direct piezoelectric voltage by means of a contactless electrostatic voltmeter Trek 370 concurrently to the strain-stress curve of the polymer sample [1]. A switch is used to periodically reset the voltage to zero by discharging the sample into a resistance load, leading to a saw-tooth recorded voltage during the tensile cycle (Figure 2b). The period of the switch is established at 1 s and the pulling speed is set to 2 mm.s⁻¹.

From Equation (3) it can be seen that g₃₁ data is obtained from the slopes of the output voltage V over stress σ. The variability of the g₃₁ coefficient is obtained by repeating the tensile cycle up to 10 times. To do so, the measurement is restricted to elastic zone of each polymer. An example of one tensile cycle measurements is represented in Figure 2c for PLLA and Figure 2d for PVDF.

$$\left|{\mathrm{g}}_{31}\right|=\frac{\mathrm{V}}{\mathrm{t}.\mathsf{\sigma }}$$

(3)

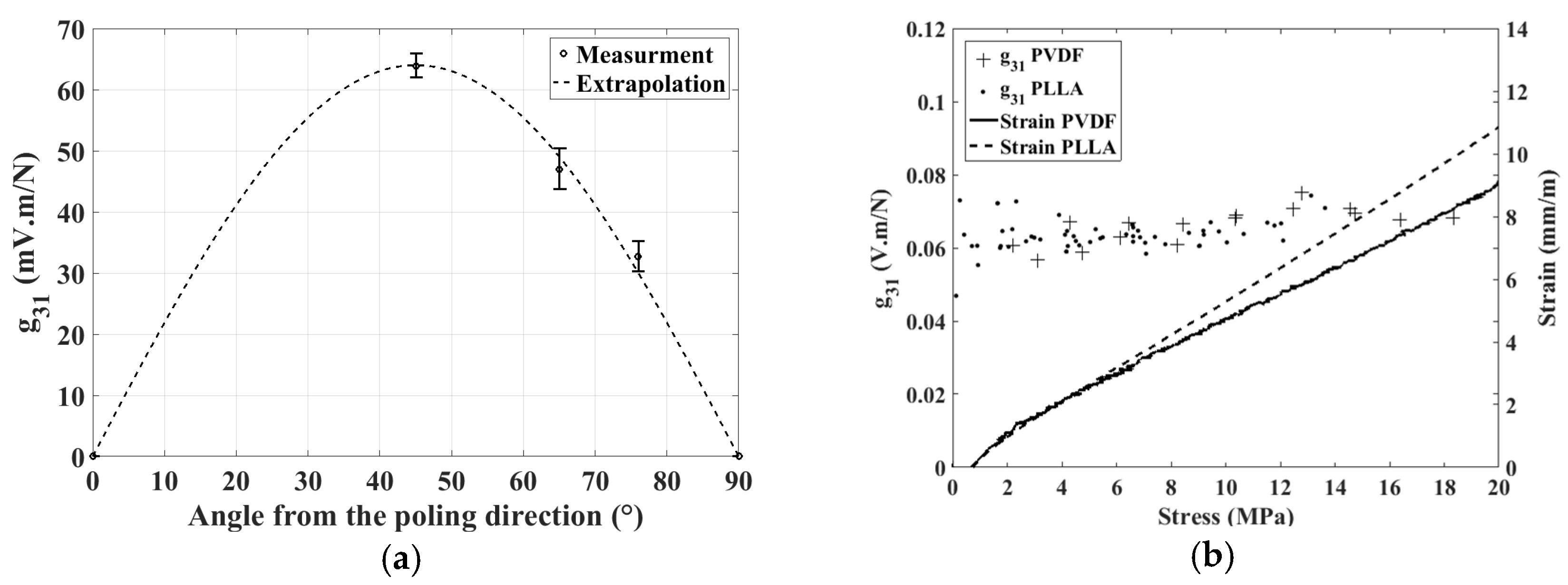
To verify the achieved properties of the PLLA film, different specimens have been cut with an angle from the polling axis. According to [1], PLLA only has one shear constant (g₁₄) that can be measured as a “g₃₁” (strain perpendicular to electric field) by cutting the sample at 45° from the stretching axis. According to [1], the measured “g₃₁” is at this point equal to 1/2 g₁₄.

The average measured “g₃₁” in Figure 3a experimentally validates the g₁₄ PLLA shear mode hypothesis, with a maximum at 45° and a decreasing coefficient to the polling axis and perpendicular to this axis. The resulting g₃₁ for both PVDF (66 ± 5 mV.m.N⁻¹) and PLLA (64 ± 7 mV.m.N⁻¹) over the stress are comparable as shown in the Figure 3b. Used as sensors, those two materials will generate the same amount of voltage. The measurements show a g₁₄ coefficient for PLLA of 128 ± 14 mV.m.N⁻¹.

2.3. Impedance Measurements

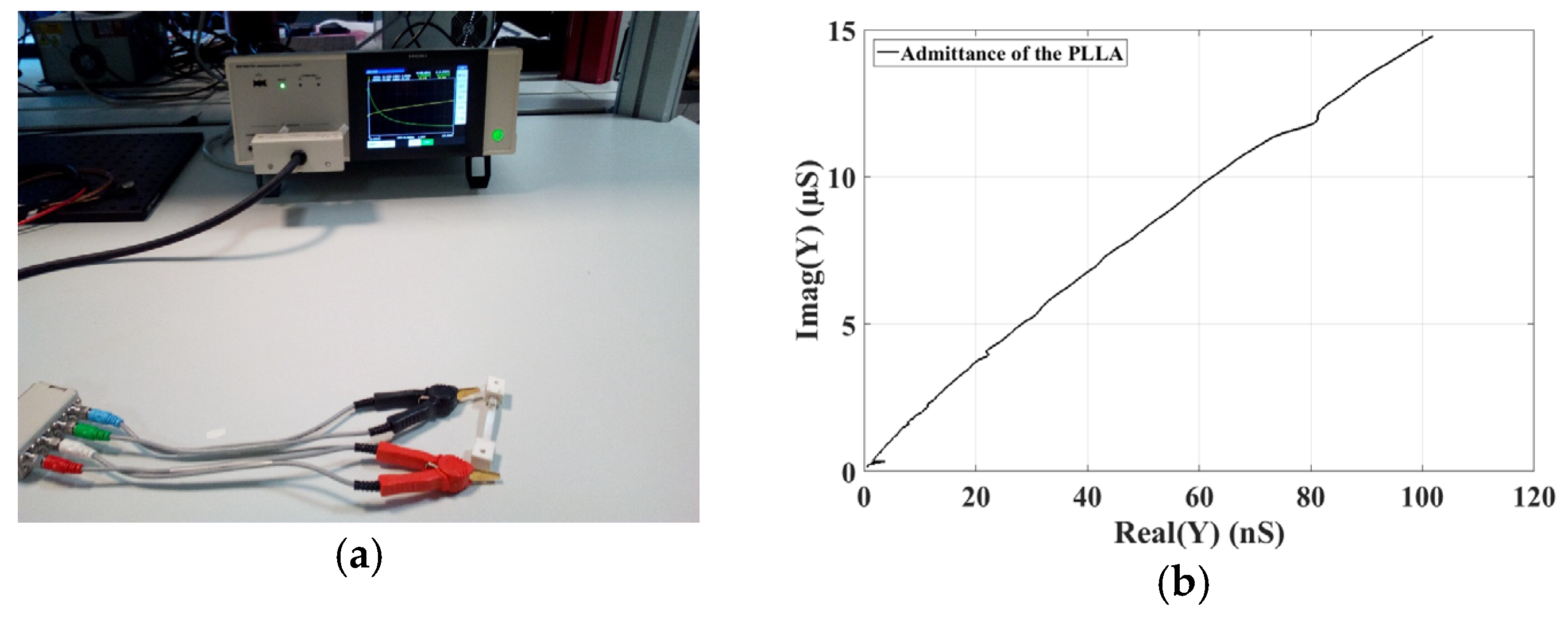
Impedance measurements are performed between 1 kHz and 100 kHz with a HIOKI impedance-meter as shown in Figure 4a,b. The equivalent electrical circuit consists on an access resistor in series with a capacitor and a resistor in parallel. The capacitor is representative of the relative dielectric constant ε₃₃ of the polymer and its parallel resistor is linked to its dielectric losses. The PVDF presents a ε₃₃ of 6.82 ± 0.01 and the PLLA of 2.82 ± 0.02.

2.4. d₃₁ Determination

From the previous measurements (ε₃₃. and g₃₁), the d₃₁ coefficient of each polymer can be extracted by means of Equation (4). More widespread than g₃₁, it represents the electro-mechanical transduction. From the calculated coefficients (

Table 1. Obtained coefficient of PVDF and PLLA.

	g31 (V.m.N−1)	c31 (GPa)	ε33	d31 (pC.N−1)	d14 (pC.N−1)
PVDF	0.066	2.10	6.82	3.98	-
PLLA	0.064	2.49	2.82	1.58 (at 45°)	3.16

), the PLLA working in d₁₄ mode is comparable to the PVDF in d₃₁ mode for the actuation. The tested PLLA film presents piezoelectric d₁₄ values below those of literature (10 × 10⁻¹² C.N⁻¹ [1] and 18.9 × 10⁻¹² C.N⁻¹ [2]) as it is still under development.

$${\mathrm{d}}_{31}={\epsilon }_{33}.{\epsilon }_0.g_{31}$$

(4)

3. Discussion and Summary

Original experimental results of in situ direct measurements of g₃₁ voltage coefficient and ε₃₃ relative dielectric coefficient of chiral PLLA and bi-axially stretched PVDF were reported. We showed great improved measurement precision (error less than 10%) on g₃₁. This is decisive for sensor, generator and energy harvesting applications. These measurements allow the calculation of the piezoelectric coefficient d₃₁ which determines actuator performance. We conclude that PLLA biopolymers are good candidates to generate electricity, comparable to PVDF. For actuator purposes, PLLA is behind PVDF because of a low ε₃₃ but its thermal drift is less important.