A Multiscale Approach to the Smart Deployment of Micro-Sensors over Flexible Plates ^†

Abstract

In former studies, we proposed a topology optimization approach to maximize the sensitivity to damage of measurements collected through a network of sensors deployed over flexible, thin plates. Within such frame, damage must be intended as a change of the structural health characterized by a reduction of the relevant load-carrying capacity. By properly comparing the response of the healthy, undamaged structure and the response of the damaged one, independently of the location of the source of damage, a procedure to optimally deploy a given set of sensors was provided. In this work we extend the aforementioned approach within a multiscale frame, to account for (at least) three different length-scales: a macroscopic one, linked to the dimensions of the structure to be monitored; a mesoscopic one, linked to the characteristic size of the damaged region(s); a microscopic one, linked to the size of inertial microelectromechanical systems (MEMS) to be used within a marginally invasive health monitoring system. Results are provided for a square plate fully clamped along its border, to show how the micro-sensors are to be deployed to maximize the sensitivity of measurements to damage, and to also discuss the speedup obtained with the proposed multiscale approach in comparison with a standard single-scale one.

1. Introduction

Civil structures are continuously exposed to external actions, not only represented by mechanical loads, that can be predicted at the design stage only in statistical sense. Progressive ageing, whose time evolution cannot be ascertained deterministically, introduces a further source of uncertainty into the structures’ lifecycle management, especially as far as maintenance is concerned. With the recent emergence of the internet of things and smart cities paradigms, it looks compulsory to think about smart, or intelligent structures, able by themselves to feel whether a formerly devised maintenance program should be modified in response to unexpected conditions. It would be of paramount importance to also design structures able to act against possible detrimental effects caused by the aforementioned unexpected, or extreme actions (like, e.g., earthquakes or typhoons) to help save lives.

Here we focus on some aspects of the mentioned self-sensing capability of smart structures, while we do not touch the point of a possible self-actuation system preventing the inception and/or growth of phenomena possibly causing local or global structural failures. In this regard, the embedment of the sensing capability into the structure requires the deployment of a sensor network all over the regions more exposed to so-called damage processes. Within the current frame, a damage is defined as a degradation of the load-carrying capacity of the structure. It can be a reduction of the local material strength or stiffness, due to environmental conditions backed by physical loading; it can be also linked to a reduction of the geometric features affecting the overall strength and stiffness characteristics of a structural component. To be more specific, with reference to lightweight composite structures (or laminates), a reduction of the mechanical properties is usually due to intra-laminar damage processes (also linked to the decohesion between the phases of the composite material), whereas a reduction of the geometrical properties can be linked to inter-laminar damages causing the decohesion of adjacent laminae. In all the cases, the physical processes are ultimately connected to micromechanically controlled events occurring inside the multi-phase material. As extensively discussed in the literature [1,2,3], such events may be difficult to ascertain as they can get incepted and grow all inside the laminated geometry, and so are difficult to catch from the outside. Accordingly, they must be indirectly assessed through a network of sensors able to sense the change in the structural behavior induced by damage [4,5].

As the processes happen inside the structure, it turns out to be physically sound to also embed the structural health monitoring (SHM) system into the structure itself [6,7,8,9]. This embedment can give rise to additional issues, as standard sensors are usually excessively large in size in comparison with the thickness of the (resin-enriched) regions between the laminae where they can be deployed during the manufacturing stage. The local distortion of the microstructure has been shown to result into a shorter lifetime of these structures, due to the inception of small defects that can eventually coalesce to provide a failure mode on their own. To avoid the SHM system to be the source of a damage, so of something that the system is supposed to feel and prevent as much as possible, in [10,11,12] we proposed to surface-mount inertial micro-sensors (MEMS) to obtain a very low invasive system.

In this work, a novel multiscale approach is proposed to deploy the sensors, so as to maximize the sensitivity of the measured structural response and then assure the identifiability of a possibly damaged area in thin, or flexible plates. By allowing for the difference in the length-scales associated with the dimensions of the structure (macroscale), of the damaged area(s) (mesoscale) and of the micro-sensors (microscale), we split the problem of optimal sensor placement into two stages: the first one deals with the identification of regions of higher sensitivity to the damage; the second one deals instead with the fine tuning of the network deployment.

Results are shown for the exemplary case already considered in [13,14], where a square plate is characterized by a damage (leading to a local reduction of the structural stiffness) of unknown intensity and position. Outcomes are provided not only in terms of optimal sensor deployment, but also in terms of speedup in the solution of the optimization problem.

2. Optimal Sensor Deployment: Multiscale Strategy

According to the theoretical/numerical frame already developed in [10,13,14], the current multiscale strategy rests on a topology optimizer that provides the optimal distribution of the sensors by maximizing a scalar measure of the change in the structural response induced by damage. Since the damage location is unknown in principle, and indeed should be also identified [5], we assume that it can be anywhere; hence, the aforementioned assessment of the change induced by the presence of damage has to be based on the comparison between the response of the healthy structure and the responses of n supplementary structures, each one featuring a pre-assigned damage in a small region only (which can be a single finite element if a numerical model is adopted). In this way, the proposed dimensionless, or scaled optimization problem reads:

$$\left\{\begin{array}{cc}\hfill & {\displaystyle \underset{x_i}{max}\psi =\sum _{j=1}^n\sum _{i=1}^n\frac{x_i\parallel {\mathbf{w}}_{ji}-{\mathbf{w}}_i\parallel }{{max}_i{x}_i\parallel {\mathbf{w}}_{ji}-{\mathbf{w}}_i\parallel }}\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & {\displaystyle 0\le x_i\le 1\mathrm{and}\sum _{i=1}^n{x}_i\le N}\hfill & \end{array}\right.$$

(1)

where: $\psi$ is the objective function to be maximized; $i=1,\cdots ,n$ is an index running over the finite elements in the mesh; $j=1,\cdots ,n$ is an additional index running over the elements where damage is located; ${\mathbf{w}}_i$ is the structural response to the loading in the undamaged case and inside the ith element (where it is considered constant, or smeared over), and ${\mathbf{w}}_{ji}$ is the response to the same loading if damage is located inside the jth element; $\parallel ·\parallel$ stands for the norm of a vector; N is the a-priori defined (scale-dependent, see below) number of sensors to be positioned; $x_i$ is a discrete element-based field adopted to denote the presence ($x_i=1$) or absence ($x_i=0$) of the sensor on the element itself. Additional details can be found in [13].

Within the present multiscale approach, N can be varied at each length-scale. For instance, in the two-scale analysis discussed in the forthcoming Section, $N_M$ and $N_m$ are respectively adopted at the macro and mesoscales. It must be also noticed that the structural response in vectors ${\mathbf{w}}_i$ and ${\mathbf{w}}_{ji}$ is scale-dependent too, since the boundary conditions have to be appropriately set along the border of the region analyzed (the whole plate at the macroscale, and the meso-regions in the subsequent fine tuning analyses). Hence, a procedure to convey the proper setting from the macroscale down to the microscale must be also devised.

3. Results

To assess the capability of the proposed multiscale approach to optimal sensor deployment, we refer to a case already treated in our former analyses, see [5,10,14]. A thin, square plate is subject to a distributed load all over its in-plane surface and is clamped along the whole boundary. The characteristic sizes linked to the three scales are set as follows: the side length of the plate, handled as macroscopic characteristic size, is $L=1$ m; the size of the damaged (square as well) region is $l=5$ cm; and the size of the MEMS sensors (like standard commercial-off-the-shelf devices available on the market) is $\ell =2.5$ mm.

As already reported in [10,14], a rather coarse mesh of $20\times 20$ quadratic elements has been adopted to discretize the plate at both scales, also in compliance with the ratios $\frac{L}{l}$ and $\frac{l}{\ell }$ between the dimensions reported here above. Such space discretization proves to be good enough as far as the deformation of the plate under the given loading is concerned. Referring to this last issue, it has been already shown that sensor deployment results to be almost independent of the kind of loading, since a concentrated force in the middle of the plate (see also [5]) would induce the same type of sensor arrangement. Results turn out to be also independent of the shape of the damaged area, as long as the finite element discretization is able to appropriately resolve the deformation field in the region surrounding the damage, so basically when the characteristic element size is smaller than the damaged area’s one.

The sensors considered to measure the variation of the response to the loadings induced by a damage of unknown magnitude and location are MEMS accelerometers. As they are also designed to feel the gravity acceleration, any rotation of the mid-plane of the plate induced by loading and, on top of all, by damage can be measured through the sensed components of the gravity acceleration in their local reference frame. To keep the symmetry in the solutions, which is mainly governed by the problem geometry, both the rotations about the two in-plane axes of a Cartesian reference frame are handled, so that a local measure of the whole rotation angle $\vartheta$ is provided by each sensor.

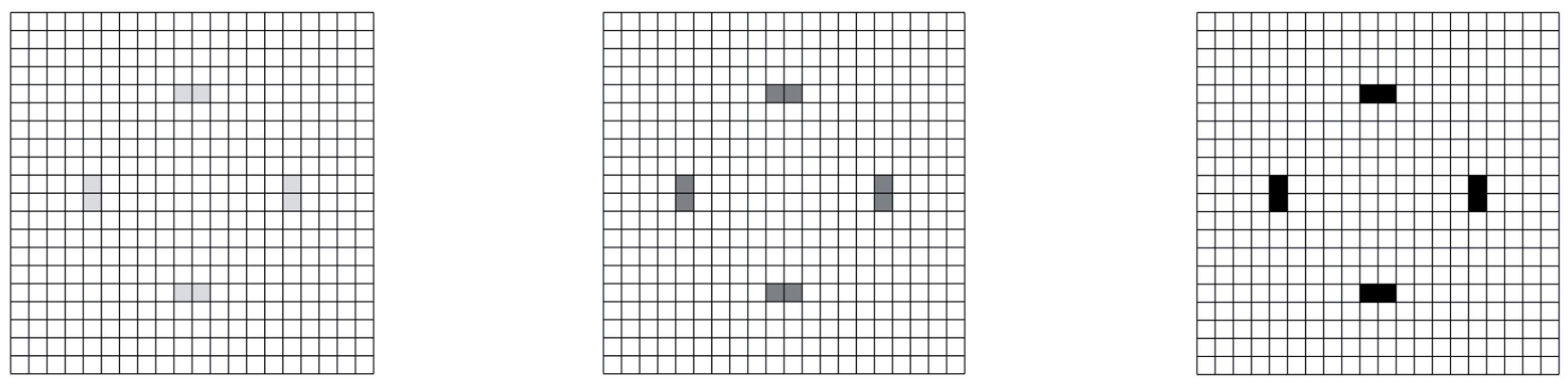
Figure 1 depicts the optimal solution obtained at the macroscale if the number of sensors to deploy in varied in the range $N_M=$1–8. As shown by the different grey level at varying $N_M$, the optimizer always identifies the same eight locations that maximize the overall sensitivity of the measured $\vartheta$ to the damage. Such locations are in compliance with the mentioned symmetry in the problem solution; with $N_M=8$, the placement of a sensor over each single meso-area (or element) is attained.

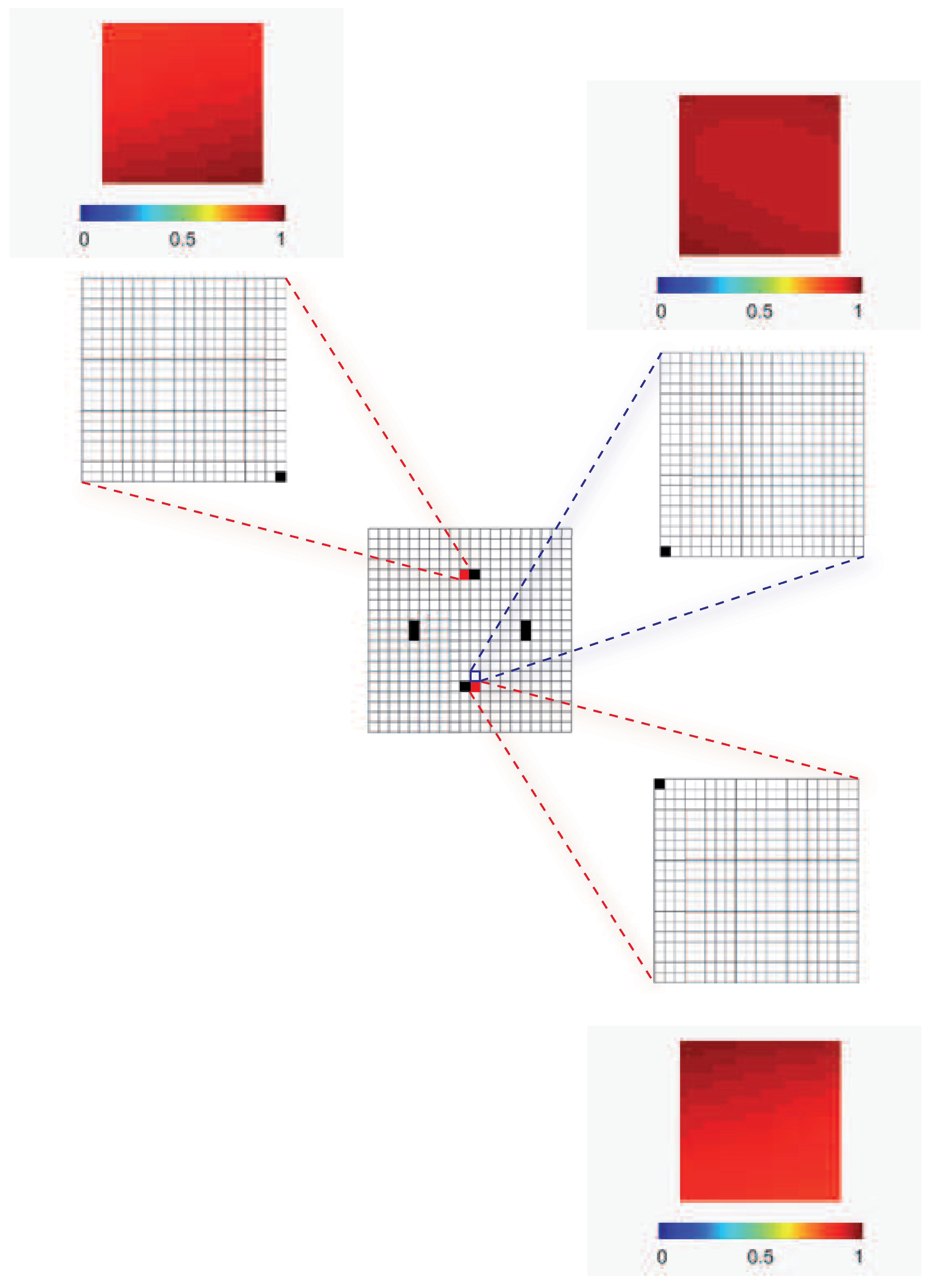
Moving from the macroscale results in Figure 1, the mesoscale analysis has been next carried out by assigning $N_m=1$ for each meso-region previously identified. In compliance with the problem symmetry at the macroscale, one single meso-region would be sufficient to provide the final results at the microscale; to further check the capability of the method to lead to consistent, or robust outcomes, independently of an ad-hoc enforcement of symmetry in the solution, the placements corresponding to two opposite mesoscale regions are reported in Figure 2 (see the shaded red regions). In this picture, not only the best sensor micro-placement is depicted (as a black area), but also the sensitivity of $\vartheta$ to damage routing the optimizer. As a further validation, the solution is sought (wrongly on purpose) in a region (blue area) nearby the one provided by the macro-analysis, to see if the optimizer still moves the sensor to the location closest to the optimal one. As shown, it turns out that the optimal and the sub-optimal placements in the chosen domains are contiguous, so the procedure overall leads to effective outcomes.

A final remark is given in terms of the speedup of the optimization procedure in comparison with a standard, single-scale one at the same resolution level, hence with the same element size of the mesoscale analysis. Such assumption implies that: with the two-scale approach $20\times 20+1=401$ analyses are required at the macroscale, plus $20\times 20+1=401$ analyses needed for each meso-region identified for placement (due to the symmetry, only one in the present case); with the single-scale approach $400\times 400+1=160,001$ analyses are required. Besides this aspect, by increasing the number of finite elements in the mesh and so the number of degrees of freedom of the problem, also the computational burden (CPU time) of each single analysis is accordingly increased, from about 0.2 s to about 49 s, when run on a personal computer featuring an Intel Core i7-4790 CPU @ 3.60 GHz processor, 16 GB RAM and running Windows 10 64 bit as operating system. Overall, the ideal speedup can be computed as $\frac{160,001\times 49}{401\times 2\times 0.2}\approx 50,000$; this datum is somehow reduced by the post-processing of the macro-scale analyses to set the appropriate input (in terms of boundary conditions) for the mesoscale ones.

4. Conclusions

In this work we have proposed a multiscale (actually, two-scale) approach to the optimal deployment of a sensor network for SHM purposes. To maximize the sensitivity to damage of the sensed local structural response, in terms of rotations with respect to the initial unloaded configuration, a topology optimization framework has been adopted. To also allow for the different dimensions of plate (or shell) structures, of the possibly damaged zones and of micro-sensors in the network, the analysis has been first carried out at the macroscale, to identify the areas of higher sensitivity of the structural response to damage, and next at the mesoscale, to better tune the placement of the MEMS sensors.

With reference to a thin square plate, fully clamped along its boundary and characterized by a damage of unknown location, it has been shown that sensors get placed by the optimizer over meso-regions in compliance with the two-fold symmetry of the problem. As for the micro-placement, results have turned out to be robustly computed by allowing only for the sensitivity to damage in the already identified meso-regions, thus providing a significant reduction of the computational costs of the whole optimization procedure.