A Fractional Computer Virus Propagation Model with Saturation Effect

Abstract

The epidemic modeling of computer virus propagation is identified as an effective approach to understanding the mechanism of virus spread. Fraction-order virus spread models exhibit remarkable advantages over their integer-order counterparts. Based on a type of bursting virus, a fractional computer virus propagation model with saturation effect is suggested. The basic properties of the model are discussed. The basic reproduction number of the model is determined. The virus–endemic equilibria of the model are determined. A criterion for the global asymptotic stability of the virus-free equilibrium is derived. For a pair of potential virus–endemic equilibria, criteria for the local asymptotic stability are presented. Some interesting properties of the model, ranging from the impact of the fractional order and the saturation index on virus spread to their coupling effect, are revealed through numerical simulations. This work helps gain a deep insight into the laws governing virus propagation.

1. Introduction

A computer virus is a type of malicious software designed to replicate itself. Once activated, it can spread from one computer to another, with the intent of performing malicious operations such as disrupting systems, corrupting data, and stealing information [1]. Computer viruses pose huge threats to several areas such as network security and digital asset protection. For example, in 2025, a large-scale hospital was attacked by the Medusa ransomware. The attackers took advantage of the unpatched Microsoft system vulnerabilities in the hospital, spread the virus through remote-control tools, encrypted about 50 TB of medical data, and demanded a ransom of RMB 110 million [2]. Consequently, the issue of defending against electronic viruses is a long-standing research hotspot in the domain of cybersecurity.

The mathematical modeling of biological infectious diseases has a history of nearly a hundred years [3]. Inspired by the high degree of similarity between digital viruses and infectious diseases, Kepart and White [4,5] proposed the earliest computer virus propagation models (See [6] for a recent review of virus propagation models). The research on virus spread models hold significant value for several reasons: (1) The way a virus spreads across networks over time can be predicted, enabling proactive preparation for potential outbreaks and resource allocation. (2) Various countermeasures (e.g., patch distribution and quarantine protocols) can be tested in a simulation environment, identifying the most effective ways to contain or mitigate infections. (3) More resilient network architectures and security mechanisms can be developed by gaining insights from propagation models, reducing susceptibility to viral attacks.

In most existing computer virus spread models, the infection rate takes the form of bilinear interaction. Due to the following reasons, the bilinear pattern significantly overestimates real-world infection rates: (1) It is unrealistically assumed that every infected device can connect with every susceptible one uniformly. In reality, network structures restrict interactions, reducing actual transmission opportunities. (2) Real-time defenses (antivirus updates, quarantines, user blocking actions, etc.) that lower effective transmission rates are rarely accounted for. (3) Varying security levels and user behavior create uneven susceptibility, making spread less efficient than the model predicts. For the purpose of accurately fitting the realistic infection rate, a spectrum of computer virus propagation models with a nonlinear infection rate have been suggested. In these models, the infection rate is of the form ${\displaystyle \frac{\beta SI}{1+\theta I}}$ [7], the form ${\displaystyle \frac{\beta SI}{1+\theta S}}$ [8,9], the form ${\displaystyle \frac{\beta SI}{1+\theta (S+I)}}$ [10,11,12], the form ${\displaystyle \frac{\beta SI}{1+{\theta }_{1}S+{\theta }_{2}I}}$ [13], the form ${\displaystyle \frac{\beta SI}{1+\theta I^2}}$ [14,15], or the form $\beta Sf\left(I\right)$ [16].

A fractional-order dynamical system is a type of mathematical framework used to describe the evolution of complex systems over time. where the dynamics are governed by fractional calculus [17]. Unlike classical integer-order dynamical systems, fractional-order systems account for memory effects of the system. This means that the current state of the system depends not only on its immediate past but also on its entire history, making it more suitable for modeling real-world phenomena with long-range dependency. In the past decade, fractional virus spread models have received considerable interest. Ref. [18] showed the existence, uniqueness, and Hyers–Ulam stability of a solution to a fractional model. Ref. [19], the authors studied a fractional model with kill signals through numerical simulations. Ref. [20] examined the asymptotic stability of a fractional model. Refs. [21,22] inspected the asymptotic stability of a pair of fractional models and presented criteria for the existence of Hopf bifurcation. In these models, the outbreak time of a virus will be later than predicted by integer-order models, and the propagation peak will be delayed. Additionally, unlike the abrupt changes in propagation rate in integer-order models, the change in virus propagation rate in fractional-order models is gentler. It can better reflect the gradual process of actual virus propagation affected by various factors (such as network topology and protective measures).

In real-world scenarios, most computer viruses are designed to enter a state of viral latency before outbreak, with the intent of infecting as many susceptible nodes as possible. In this context, it is proper to characterize the propagation process of a virus by means of a Susceptible-Latent-Bursting-Susceptible (SLBS) model, where ’susceptible’ represents the state of not being infected with a virus; ‘latent’ represents the state of being infected with a propagating virus, but not performing virus-induced destructive operations; ‘bursting’ describes the state of being infected with a propagation virus and performing virus-induced destructive operations; and the transition from the latent state to the bursting state represents a virus in latency that starts performing malicious operations other than infections (see [23,24,25] for ordinary SLBS models and [26,27,28] for delayed SLBS models). Later, some variants of the SLBS models, which are known as the Susceptible-Latent-Bursting-Recovered-Susceptible (SLBRS) models, have been advised [29,30,31]. In an SLBRS model, an added state known as ‘recovered’ is accounted for to reflect the repair of outbreak nodes.

In the framework of SLBS viruses, this article advises a Caputo fractional computer virus propagation model with a nonlinear saturation infection rate. Our work is closely related to that of [25], where a generic nonlinear infection rate is assumed; the work is conducted on an integer-order virus spread model. In our article, the well-known Holling type II saturation infection rate is introduced, and the model is extended to the situation of fraction-order virus propagation.

The subsequent materials of this article are organized as follows: Section 2 provides basic notations and terminologies. Section 3 formulates the virus propagation model. Section 4 discusses the basic properties of the model. Section 5 figures out the basic reproduction number of the model. Section 6 determines the virus–endemic equilibria of the model. Section 7 gives a criterion for the global asymptotic stability of the virus-free equilibrium. Section 8 derives a criterion for the local asymptotic stability of the virus–endemic equilibrium with no latent component. Section 9 reports a criterion for the local asymptotic stability of the virus–endemic equilibrium with a non-zero latent component. Section 10 validates the theoretical findings through numerical simulations. Section 11 conducts further discussions. This work is summarized in Section 12.

2. Notations and Terminologies

This section introduces the basic notations and terminologies that will be used in the subsequent research.

Definition 1.

The Mittag-Leffler function with parameter $\alpha \ge 0$ is defined as follows:

$$E_{\alpha }\left(z\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{z^k}{\Gamma (\alpha k+1)}}.$$

(1)

The Mittag-Leffler function with parameters $\alpha \ge 0$ and $\beta \ge 0$ is defined as follows:

$$E_{\alpha ,\beta }\left(z\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{z^k}{\Gamma (\alpha k+\beta )}}.$$

(2)

Here, $\Gamma (·)$ represents the Gamma function.

Definition 2.

Let $0<\alpha <1$. The α-order Caputo derivative of the function f is defined as follows:

$$D^{\alpha }f\left(t\right)={\displaystyle \frac{1}{\Gamma (1-\alpha )}}{\int }_0^t{\displaystyle \frac{f^{\prime }\left(s\right)}{{(t-s)}^{\alpha }}}ds.$$

(3)

Lemma 1

([17]). Let $0<\alpha <1$, $x:[0,\infty )\to {\mathbb{R}}^n$, $f:[0,\infty )\times {\mathbb{R}}^n\to {\mathbb{R}}^n$. Consider the following fractional differential equation:

$$D^{\alpha }x\left(t\right)=f(t,x\left(t\right)),x\left(0\right)=x_0.$$

(4)

Suppose the following conditions are met:

(C1) 

f is continuous in the region $[0,\infty )\times {\mathbb{R}}^n$.

(C2) 

f is globally Lipschitz continuous with respect to x, i.e., there exists a positive constant C such that the following is true:

$$\Vert f(t,x_1)-f(t,x_2)\Vert \le C\Vert x_1-x_2\Vert ,\forall x_1,x_2\in {\mathbb{R}}^n.$$

(5)

Then, Equation (4) admits a unique solution.

Lemma 2

([17]). Let $0<\alpha <1$, $x:[0,\infty )\to {\mathbb{R}}^n$, A is a real matrix of order n, $\{{\lambda }_1,\dots ,{\lambda }_n\}$ denotes the spectrum of A. Consider the following linear fractional differential equation:

$$D^{\alpha }x\left(t\right)=Ax\left(t\right).$$

(6)

The following assertions hold:

(A1) 

Suppose all ${\lambda }_i$ meet $|arg\left({\lambda }_i\right)|>{\displaystyle \frac{\alpha \pi }{2}}$. Then, the origin is locally asymptotically stable.

(A2) 

Suppose there exists ${\lambda }_i$ such that $|arg\left({\lambda }_i\right)|<{\displaystyle \frac{\alpha \pi }{2}}$. Then, the origin is unstable.

Lemma 3

([17]). Let $0<\alpha <1$, $a,b>0$. Suppose $D^{\alpha }x\left(t\right)=a-bx\left(t\right),t\ge 0$. Then, the following is true:

$$x\left(t\right)={\displaystyle \frac{a}{b}}+\left[x\left(0\right)-{\displaystyle \frac{a}{b}}\right]E_{\alpha }(-b{t}^{\alpha }).$$

(7)

Lemma 4

([17]). Let $0<\alpha <1$, $c>0$. Suppose $D^{\alpha }x\left(t\right)\ge -cx\left(t\right),t\ge 0$. Then, the following is true:

$$x\left(t\right)\ge x\left(0\right)E_{\alpha }(-c{t}^{\alpha }).$$

(8)

3. A Fractional Computer Virus Propagation Model

Consider an organization (an enterprise, a research institute, a government sector, etc.). Suppose the computers in the organization are interconnected by a group of computers to form an intranet. For brevity, all computers within the network are referred to as internal, whereas all computers outside the network are referred to as external. Owing to different reasons, every internal computer may possibly be physically disconnected from the network to become a part outside the intranet, whereas every external computer may possibly be physically connected to the network to become a part of the intranet.

Under the threat of a specific virus, assume (a) every internal computer is either susceptible (not infected with the virus), latent (infected with the virus and performing infection operations only), or bursting (infected with the virus and performing malicious operations including infections); (b) every external computer is susceptible. Let $S\left(t\right)$ (resp. $L\left(t\right)$, $B\left(t\right)$) denote the number of susceptible (resp. latent, bursting) internal computers at time t. The following assumptions are introduced:

($A_1$)

External computers are physically connected to the network at constant rate $\mu >0$ (entrance rate).

($A_2$)

Every internal computer is physically disconnected from the network at constant rate $\delta >0$ (exit rate).

($A_3$)

When contacting with latent computers, susceptible internal computers become infected, do not perform virus-induced destructive operations, and hence become latent at time t at rate ${\displaystyle \frac{\beta S\left(t\right)L\left(t\right)}{1+\sigma \left[L\right(t)+B(t\left)\right]}}$. Here, the constant $\beta >0$ is referred to as the infection force, while the constant $\sigma >0$ is referred to as the saturation index.

($A_4$)

When contacting with bursting computers, susceptible internal computers become infected, perform virus-induced destructive operations, and hence become bursting at time t at rate ${\displaystyle \frac{\beta S\left(t\right)B\left(t\right)}{1+\sigma \left[L\right(t)+B(t\left)\right]}}$.

($A_5$)

Due to transition from latency to burst, every latent computer becomes bursting at rate $\eta >0$ (burst rate).

($A_6$)

Due to recovery from burst, every bursting computer becomes susceptible at rate $\gamma >0$ (recovery rate).

($A_7$)

Let $\alpha$ denote the order of the Caputo derivative used in the subsequent modeling. Assume $0<\alpha <1$.

The above assumptions lead to the following fractional computer virus propagation model:

$$\left\{\begin{array}{cc}\hfill D^{\alpha }S\left(t\right)& =\mu -{\displaystyle \frac{\beta S\left(t\right)\left[L\right(t)+B(t\left)\right]}{1+\sigma \left[L\right(t)+B(t\left)\right]}}+\gamma B\left(t\right)-\delta S\left(t\right),t\ge 0,\hfill \\ \hfill D^{\alpha }L\left(t\right)& ={\displaystyle \frac{\beta S\left(t\right)L\left(t\right)}{1+\sigma \left[L\right(t)+B(t\left)\right]}}-\eta L\left(t\right)-\delta L\left(t\right),t\ge 0,\hfill \\ \hfill D^{\alpha }B\left(t\right)& ={\displaystyle \frac{\beta S\left(t\right)B\left(t\right)}{1+\sigma \left[L\right(t)+B(t\left)\right]}}+\eta L\left(t\right)-\gamma B\left(t\right)-\delta B\left(t\right),t\ge 0,\hfill \\ \hfill S\left(0\right)& \ge 0,L\left(0\right)\ge 0,B\left(0\right)\ge 0.\hfill \end{array}\right.$$

(9)

Remark 1.

The first and main approach to establishing a fractional compartment model is by directly introducing a fractional-order derivative to yield the fractional model (not by simply replacing the regular derivative in a compartment model with a fractional-order derivative to yield the fractional model). A so-constructed fractional model has a striking advantage—in parallel to its integer-order counterpart, the dynamics of the model can be investigated theoretically, yielding rich conclusions. Consequently, most existing fractional compartment models, including model (9), are constructed in this way. In the research of such a fractional model, the units of all the associated rates may be uniformly set as ${\displaystyle \frac{1}{tim{e}^{\alpha }}}$. As a result, both sides of the model have the same unit.

Remark 2.

The second approach to establishing a fractional compartment model is by introducing a stochastic process to derive the fractional model [32,33]. A so-constructed fractional model is typically explainable, with the disadvantage of being highly complex and difficult for theoretical research.

4. Basic Properties

This section examines the basic properties of the solution to the model (9). First, inspect the non-negativity of the solution.

Lemma 5.

Consider the model (9). Then, $S\left(t\right)\ge 0$, $L\left(t\right)\ge 0$, $B\left(t\right)\ge 0$, $\forall t\ge 0$.

Proof of Lemma 5.

On the contrary, suppose there exists $t_1>0$ such that (a) $S\left(t\right)\ge 0$, $L\left(t\right)\ge 0$, $B\left(t\right)\ge 0$, $\forall 0\le t<t_1$, (b) $S\left(t_1\right)<0$, $L\left(t_1\right)<0$, or $B\left(t_1\right)<0$. Consider the following three possibilities.

Case 1: $S\left(t_1\right)<0$. It follows from the first equation of Equation (9) that the following is true:

$$\begin{array}{cc}\hfill D^{\alpha }S\left(t\right)& =\mu -{\displaystyle \frac{\beta S\left(t\right)\left[L\right(t)+B(t\left)\right]}{1+\sigma \left[L\right(t)+B(t\left)\right]}}+\gamma B\left(t\right)-\delta S\left(t\right)\hfill \\ \hfill & \ge -{\displaystyle \frac{\beta S\left(t\right)\left[L\right(t)+B(t\left)\right]}{1+\sigma \left[L\right(t)+B(t\left)\right]}}-\delta S\left(t\right),\forall 0\le t<t_1.\hfill \end{array}$$

(10)

Let

$$f\left(x\right)={\displaystyle \frac{x}{1+\sigma x}},x\ge 0.$$

(11)

Then,

$$f^{\prime }\left(x\right)={\displaystyle \frac{1}{{(1+\sigma x)}^2}}>0,x\ge 0.$$

(12)

So,

$$f\left(x\right)<f(+\infty )={\displaystyle \frac{1}{\sigma }},x\ge 0.$$

(13)

Thus,

$$f(L\left(t\right)+B\left(t\right))={\displaystyle \frac{L\left(t\right)+B\left(t\right)}{1+\sigma \left[L\right(t)+B(t\left)\right]}}<{\displaystyle \frac{1}{\sigma }},0\le t<t_1.$$

(14)

Hence, it follows from Equation (10) that the following is true:

$$D^{\alpha }S\left(t\right)\ge -\left({\displaystyle \frac{\beta }{\sigma }}+\delta \right)S\left(t\right),\forall 0\le t<t_1.$$

(15)

It follows from Lemma 4 that the following is true:

$$S\left(t\right)\ge S\left(0\right)E_{\alpha }\left(-\left({\displaystyle \frac{\beta }{\sigma }}+\delta \right)t^{\alpha }\right),\forall 0\le t<t_1.$$

(16)

Hence,

$$S\left(t_1\right)=limS\left(t_1^{-}\right)\ge S\left(0\right)E_{\alpha }\left(-\left({\displaystyle \frac{\beta }{\sigma }}+\delta \right)t_1^{\alpha }\right)\ge 0.$$

(17)

This contradicts the assumption of $S\left(t_1\right)<0$.

Case 2: $L\left(t_1\right)<0$. It follows from the second equation of Equation (9) that the following is true:

$$\begin{array}{cc}\hfill D^{\alpha }L\left(t\right)& ={\displaystyle \frac{\beta S\left(t\right)L\left(t\right)}{1+\sigma \left[L\right(t)+B(t\left)\right]}}-\eta L\left(t\right)-\delta L\left(t\right)\hfill \\ \hfill & \ge -(\eta +\delta )L\left(t\right),\forall 0\le t<t_1.\hfill \end{array}$$

(18)

It follows from Lemma 4 that the following is true:

$$L\left(t\right)\ge L\left(0\right)E_{\alpha }(-(\eta +\delta )t^{\alpha }),\forall 0\le t<t_1.$$

(19)

Hence,

$$L\left(t_1\right)=limL\left(t_1^{-}\right)\ge L\left(0\right)E_{\alpha }(-(\eta +\delta )t_1^{\alpha })\ge 0.$$

(20)

This contradicts the assumption of $L\left(t_1\right)<0$.

Case 3: $B\left(t_1\right)<0$. It follows from the third equation of Equation (9) that the following is true:

$$\begin{array}{cc}\hfill D^{\alpha }B\left(t\right)& ={\displaystyle \frac{\beta S\left(t\right)B\left(t\right)}{1+\sigma \left[L\right(t)+B(t\left)\right]}}+\alpha L\left(t\right)-\gamma B\left(t\right)-\delta B\left(t\right)\hfill \\ \hfill & \ge -(\gamma +\delta )L\left(t\right),\forall 0\le t<t_1.\hfill \end{array}$$

(21)

It follows from Lemma 4 that the following is true:

$$B\left(t\right)\ge B\left(0\right)E_{\alpha }(-(\gamma +\delta )t^{\alpha }),\forall 0\le t<t_1.$$

(22)

Hence,

$$B\left(t_1\right)=limB\left(t_1^{-}\right)=B\left(0\right)E_{\alpha }(-(\gamma +\delta )t_1^{\alpha })\ge 0.$$

(23)

This contradicts the assumption of $L\left(t_1\right)<0$.

The assertion holds based on the principle of reduction to absurdity. □

Second, inspect the boundedness of the solution.

Lemma 6.

The solution to model (9) is bounded.

Proof of Lemma 6.

Let $N\left(t\right)=S\left(t\right)+I\left(t\right)+R\left(t\right)$ denote the total number of internal nodes at time t. Adding the three equations in model (9) yields the following:

$$D^{\alpha }N\left(t\right)=\mu -\delta N\left(t\right),t\ge 0.$$

(24)

So,

$$N\left(t\right)={\displaystyle \frac{\mu }{\delta }}+\left[N\left(0\right)-{\displaystyle \frac{\mu }{\delta }}\right]E_{\alpha }(-\delta t^{\alpha }),t\ge 0,$$

(25)

Notice that $0\le E_{\alpha }(-\delta t^{\alpha })\le 1$. It follows that:

$$\begin{array}{cc}\hfill N\left(t\right)& =\left|{\displaystyle \frac{\mu }{\delta }}+\left[N\left(0\right)-{\displaystyle \frac{\mu }{\delta }}\right]E_{\alpha }(-\delta t^{\alpha })\right|\hfill \\ \hfill & \le {\displaystyle \frac{\mu }{\delta }}+\left|\left[N\left(0\right)-{\displaystyle \frac{\mu }{\delta }}\right]E_{\alpha }(-\delta t^{\alpha })\right|\hfill \\ \hfill & \le {\displaystyle \frac{\mu }{\delta }}+\left|N\left(0\right)-{\displaystyle \frac{\mu }{\delta }}\right|=M.\hfill \end{array}$$

(26)

In view of Lemma 5, the solution to the model (9) is bounded by the following set:

$$\Omega =\left\{(S,L,B)\in {\mathbb{R}}_{+}^3:S+L+B\le M\right\}.$$

(27)

□

Finally, examine the existence and uniqueness of the solution.

Lemma 7.

The solution to model (9) is existent and unique.

The proof of this lemma is shown in Appendix A.

It follows from Equation (9) that $N\left(t\right)\to {\displaystyle \frac{\mu }{\delta }}$. Hence, the plane $S+L+B={\displaystyle \frac{\mu }{\delta }}$ is an invariant manifold of model (9) that is attracting in the first octant. According to [34,35], it follows that model (9) can be reduced to the following model:

$$\left\{\begin{array}{cc}\hfill D^{\alpha }L\left(t\right)& ={\displaystyle \frac{\beta [\frac{\mu }{\delta }-L\left(t\right)-B\left(t\right)]L\left(t\right)}{1+\sigma \left[L\right(t)+B(t\left)\right]}}-\eta L\left(t\right)-\delta L\left(t\right),\hfill \\ \hfill D^{\alpha }B\left(t\right)& ={\displaystyle \frac{\beta [\frac{\mu }{\delta }-L\left(t\right)-B\left(t\right)]B\left(t\right)}{1+\sigma \left[L\right(t)+B(t\left)\right]}}+\eta L\left(t\right)-\gamma B\left(t\right)-\delta B\left(t\right),t\ge 0.\hfill \end{array}\right.$$

(28)

In what follows, this model will be the focus of attention.

5. Basic Reproduction Number

Now, consider the basic reproduction number of model (28).

Theorem 1.

Let

$$R_1={\displaystyle \frac{\beta \mu }{\delta (\eta +\delta )}},R_2={\displaystyle \frac{\beta \mu }{\delta (\gamma +\delta )}}.$$

(29)

The basic reproduction number of model (28) equals the following:

$$R_0=max(R_1,R_2).$$

(30)

Proof of Theorem 1.

Let $F_1\left(t\right)$ (resp. $F_2\left(t\right)$) denote the rate of appearance of new latent (bursting) nodes at time t, $V_1^{-}\left(t\right)$ (resp. $V_2^{-}\left(t\right)$) denote the rate of transfer of nodes out of the latent (resp. bursting) compartment at time t, and $V_1^{+}\left(t\right)$ (resp. $V_2^{+}\left(t\right)$) denote the rate of transfer of nodes into the latent (resp. bursting) compartment by all other means at time t. Then, the following is true:

$$F_1\left(t\right)={\displaystyle \frac{\beta [\frac{\mu }{\delta }-L\left(t\right)-B\left(t\right)]L\left(t\right)}{1+\sigma \left[L\right(t)+B(t\left)\right]}},F_2\left(t\right)={\displaystyle \frac{\beta [\frac{\mu }{\delta }-L\left(t\right)-B\left(t\right)]B\left(t\right)}{1+\sigma \left[L\right(t)+B(t\left)\right]}},$$

(31)

$$V_1^{-}\left(t\right)=\eta L\left(t\right)+\delta L\left(t\right),V_2^{-}\left(t\right)=\gamma B\left(t\right)+\delta B\left(t\right),$$

(32)

$$V_1^{+}\left(t\right)=0,V_2^{+}\left(t\right)=\eta L\left(t\right).$$

(33)

Let

$$V_1\left(t\right)=V_1^{-}\left(t\right)-V_1^{+}\left(t\right)=\eta L\left(t\right)+\delta L\left(t\right),$$

(34)

$$V_2\left(t\right)=V_2^{-}\left(t\right)-V_2^{+}\left(t\right)=\gamma B\left(t\right)+\delta B\left(t\right)-\eta L\left(t\right).$$

(35)

Then,

$$D^{\alpha }L\left(t\right)=F_1\left(t\right)-V_1\left(t\right),D^{\alpha }B\left(t\right)=F_2\left(t\right)-V_2\left(t\right).$$

(36)

Let

$$F\left(t\right)={(F_1\left(t\right),F_2\left(t\right))}^T,V\left(t\right)={(V_1\left(t\right),V_2\left(t\right))}^T.$$

(37)

Let $E_0=(0,0)$. Let $DF\left(t\right)$ (resp. $DV\left(t\right)$) denote the Jacobian matrix of $F\left(t\right)$ (resp. $V\left(t\right)$). Let ${F=DF\left(t\right)|}_{E_0}$ (resp. ${V=DV\left(t\right)|}_{E_0}$) denote the $DF\left(t\right)$ (resp. $DV\left(t\right)$) evaluated at $E_0$. Then, the following is true:

$$F=\left[\begin{array}{cc}{\displaystyle \frac{\partial F_1\left(t\right)}{\partial L\left(t\right)}}{|}_{E_0}& {\displaystyle \frac{\partial F_1\left(t\right)}{\partial B\left(t\right)}}{|}_{E_0}\\ {\displaystyle \frac{\partial F_2\left(t\right)}{\partial L\left(t\right)}}{|}_{E_0}& {\displaystyle \frac{\partial F_2\left(t\right)}{\partial B\left(t\right)}}{|}_{E_0}\end{array}\right]=\left[\begin{array}{cc}{\displaystyle \frac{\beta \mu }{\delta }}& 0\\ 0& {\displaystyle \frac{\beta \mu }{\delta }}\end{array}\right].$$

(38)

$$V=\left[\begin{array}{cc}{\displaystyle \frac{\partial V_1\left(t\right)}{\partial L\left(t\right)}}{|}_{E_0}& {\displaystyle \frac{\partial V_1\left(t\right)}{\partial B\left(t\right)}}{|}_{E_0}\\ {\displaystyle \frac{\partial V_2\left(t\right)}{\partial L\left(t\right)}}{|}_{E_0}& {\displaystyle \frac{\partial V_2\left(t\right)}{\partial B\left(t\right)}}{|}_{E_0}\end{array}\right]=\left[\begin{array}{cc}\eta +\delta & 0\\ -\eta & \gamma +\delta \end{array}\right].$$

(39)

So,

$$F{V}^{-1}=\left[\begin{array}{cc}{\displaystyle \frac{\beta \mu }{\delta }}& 0\\ 0& {\displaystyle \frac{\beta \mu }{\delta }}\end{array}\right]{\left[\begin{array}{cc}\eta +\delta & 0\\ -\eta & \gamma +\delta \end{array}\right]}^{-1}={\displaystyle \frac{\beta \mu }{\delta }}\left[\begin{array}{cc}{\displaystyle \frac{1}{\eta +\delta }}& 0\\ {\displaystyle \frac{1}{(\gamma +\delta )(\eta +\delta )}}& {\displaystyle \frac{1}{\gamma +\delta }}\end{array}\right],$$

(40)

which admits the following pair of eigenvalues: ${\lambda }_1=R_1$, ${\lambda }_2=R_2$. Let $\rho \left(F{V}^{-1}\right)$ denote the spectral radius of $F{V}^{-1}$. It follows by applying the next-generation matrix method [36,37] that:

$$\begin{array}{cc}\hfill R_0=\rho \left(F{V}^{-1}\right)& =max({\lambda }_1,{\lambda }_2)=max(R_1,R_2).\hfill \end{array}$$

(41)

□

Remark 3.

According to Theorem 1, $R_0$ is determined by the relative location of η and γ. Specifically, $R_0=R_1$ or $R_0=R_2$ as long as $\eta <\gamma$ or $\eta >\gamma$. This is an interesting outcome.

6. Virus–Endemic Equilibria

In all cases, model (28) admits the virus-free equilibrium $E_0=(0,0)$. This section investigates the virus–endemic equilibria of model (28). For convenience, we introduce the following terminology.

Definition 3.

Let $E^{*}=(L^{*},B^{*})$ be a virus–endemic equilibrium of model (28).

(D1) 

$E^{*}$ is referred to as 0+ if $L^{*}=0$, $B^{*}>0$.

(D2) 

$E^{*}$ is referred to as +0 if $L^{*}>0$, $B^{*}=0$.

(D3) 

$E^{*}$ is referred to as ++ if $L^{*}>0$, $B^{*}>0$.

Theorem 2.

The following assertions hold.

(A1) 

Model (28) admits no +0 virus–endemic equilibrium.

(A2) 

Model (28) admits a 0+ virus–endemic equilibrium if and only if $R_2>1$. In this case, model (28) admits the following unique virus–endemic equilibrium:

$$E_1=(L_1,B_1)=\left(0,{\displaystyle \frac{(\gamma +\delta )(R_2-1)}{\beta +(\gamma +\delta )\sigma }}\right).$$

(42)

(A3) 

Model (28) admits a ++ virus–endemic equilibrium if and only if $R_1>1$, $\gamma >\eta$. In this case, model (28) admits the following unique virus–endemic equilibrium:

$$E_2=(L_2,B_2)=\left({\displaystyle \frac{(\gamma -\eta )(\eta +\delta )(R_1-1)}{\gamma [\beta +(\eta +\delta \left)\sigma \right]}},{\displaystyle \frac{\eta (\eta +\delta )(R_1-1)}{\gamma [\beta +(\eta +\delta \left)\sigma \right]}}\right).$$

(43)

Proof of Theorem 2.

Let $E^{*}=(L^{*},B^{*})$ be a virus–endemic equilibrium of model (28). Then, either $L^{*}>0$ or $B^{*}>0$, as follows:

$${\displaystyle \frac{\beta (\frac{\mu }{\delta }-L^{*}-B^{*})L^{*}}{1+\sigma (L^{*}+B^{*})}}-\eta L^{*}-\delta L^{*}=0,$$

(44)

and

$${\displaystyle \frac{\beta (\frac{\mu }{\delta }-L^{*}-B^{*})B^{*}}{1+\sigma (L^{*}+B^{*})}}+\eta L^{*}-\gamma B^{*}-\delta B^{*}=0.$$

(45)

Consider three possibilities.

Case 1. $L^{*}>0$, $B^{*}=0$. It follows from Equation (45) that $L^{*}=0$. A contradiction occurs. Hence, model (28) admits no +0 virus–endemic equilibrium.

Case 2. $L^{*}=0$, $B^{*}>0$. It follows from Equation (45) that:

$${\displaystyle \frac{\beta (\frac{\mu }{\delta }-B^{*})}{1+\sigma B^{*}}}-\gamma -\delta =0.$$

(46)

So,

$$B^{*}={\displaystyle \frac{(\gamma +\delta )(R_2-1)}{\beta +(\gamma +\delta )\sigma }}.$$

(47)

This implies $R_2>1$.

Consequently, model (28) admits a 0+ virus–endemic equilibrium if and only if $R_2>1$. In this case, model (28) admits the following unique virus-endemic equilibrium:

$$E_1=\left(0,{\displaystyle \frac{(\gamma +\delta )(R_2-1)}{\beta +(\gamma +\delta )\sigma }}\right).$$

(48)

Case 3. $L^{*}>0$, $B^{*}>0$. It follows from Equation (44) that:

$${\displaystyle \frac{\beta (\frac{\mu }{\delta }-L^{*}-B^{*})}{1+\sigma (L^{*}+B^{*})}}=\eta +\delta .$$

(49)

So,

$$[\beta +(\eta +\delta )\sigma ](L^{*}+B^{*})=(\eta +\delta )(R_1-1).$$

(50)

This implies $R_1>1$. Solving Equation (50) for $L^{*}$ leads to the following:

$$L^{*}={\displaystyle \frac{(\eta +\delta )(R_1-1)}{\beta +(\eta +\delta )\sigma }}-B^{*}.$$

(51)

It follows by substituting Equation (49) into Equation (45) that:

$$(\eta +\delta )B^{*}+\eta L^{*}-\gamma B^{*}-\delta B^{*}=0.$$

(52)

So,

$$L^{*}={\displaystyle \frac{(\gamma -\eta )B^{*}}{\eta }}.$$

(53)

This implies $\gamma >\eta$. Substituting Equation (53) into Equation (51) yields the following:

$$B^{*}={\displaystyle \frac{\eta (\eta +\delta )(R_1-1)}{\gamma [\beta +(\eta +\delta \left)\sigma \right]}}.$$

(54)

It follows from Equation (53) that:

$$L^{*}={\displaystyle \frac{(\gamma -\eta )(\eta +\delta )(R_1-1)}{\gamma [\beta +(\eta +\delta \left)\sigma \right]}}.$$

(55)

Consequently, model (28) admits a ++ virus–endemic equilibrium if and only if $R_1>1$ and $\gamma >\eta$. In this case, model (28) admits the following unique virus–endemic equilibrium:

$$E_2=\left({\displaystyle \frac{(\gamma -\eta )(\eta +\delta )(R_1-1)}{\gamma [\beta +(\eta +\delta \left)\sigma \right]}},{\displaystyle \frac{\eta (\eta +\delta )(R_1-1)}{\gamma [\beta +(\eta +\delta \left)\sigma \right]}}\right).$$

(56)

□

Remark 4.

There are several reasons why it is difficult to obtain real data on computer virus spread. First, due to concerns about reputation damage, legal issues, or the fear of revealing security vulnerabilities, many individuals and organizations are reluctant to report virus infections, leading to a significant amount of unrecorded cases. Second, computer viruses can mutate rapidly, with different strains having varying transmission routes and infection patterns. This variability makes it hard to track and aggregate consistent data. Next, viruses often spread through covert channels such as encrypted communications, unmonitored networks, or malicious software embedded in legitimate programs, which are difficult to detect and trace. Finally, there is no global or universal standard for collecting and reporting virus spread data. Different institutions and regions may use different metrics and methods, resulting in fragmented and incomparable data. Consequently, all the subsequent experiments shall be conducted based on fictional data, aiming to reveal the mechanism of computer virus spread.

Example 1.

Consider model (28) with $\alpha =0.8$, $\mu =80$, $\delta =1$, $\beta =0.015$, $\eta =1$, $\gamma =0.5$, and $\sigma =0.6$. It is easily verified that $R_1<1$, $R_2<1$. Hence, it follows from Theorem 2 that model (23) admits no virus–endemic equilibrium.

Example 2.

Consider model (28) with $\alpha =0.8$, $\mu =40$, $\delta =1$, $\beta =0.15$, $\eta =1$, $\gamma =0.5$, and $\sigma =0.01$. It is easily verified that $R_2>1$. Hence, it follows from Theorem 2 that model (23) admits the virus–endemic equilibrium $E_1$.

Example 3.

Consider model (28) with $\alpha =0.8$, $\mu =40$, $\delta =1$, $\beta =0.15$, $\eta =1$, $\gamma =2$, and $\sigma =0.01$. It is easily verified that $R_1>1$, $\gamma >\eta$. Hence, it follows from Theorem 2 that model (23) admits the virus–endemic equilibrium $E_2$.

7. Asymptotic Stability of the Equilibrium ${\mathit{E}}_{\mathbf{0}}$

This section examines the asymptotic stability of the virus-free equilibrium $E_0$.

Let

$$\left\{\begin{array}{cc}\hfill f_1(x\left(t\right),y\left(t\right))& ={\displaystyle \frac{\beta [\frac{\mu }{\delta }-x\left(t\right)-y\left(t\right)]x\left(t\right)}{1+\sigma \left[x\right(t)+y(t\left)\right]}}-\eta x\left(t\right)-\delta x\left(t\right),\hfill \\ \hfill f_2(x\left(t\right),y\left(t\right))& ={\displaystyle \frac{\beta [\frac{\mu }{\delta }-x\left(t\right)-y\left(t\right)]y\left(t\right)}{1+\sigma \left[x\right(t)+y(t\left)\right]}}+\eta x\left(t\right)-\gamma y\left(t\right)-\delta y\left(t\right).\hfill \end{array}\right.$$

(57)

The linearized system of the model (28) at $E_0$ is as follows:

$$\left\{\begin{array}{cc}\hfill D^{\alpha }x\left(t\right)& ={\displaystyle \frac{\partial f_1(x\left(t\right),y\left(t\right))}{\partial x\left(t\right)}}{{|}_{(x\left(t\right),y\left(t\right))=E_0}x\left(t\right)+{\displaystyle \frac{\partial f_1(x\left(t\right),y\left(t\right))}{\partial y\left(t\right)}}|}_{(x\left(t\right),y\left(t\right))=E_0}y\left(t\right),\hfill \\ \hfill D^{\alpha }y\left(t\right)& ={\displaystyle \frac{\partial f_2(x\left(t\right),y\left(t\right))}{\partial x\left(t\right)}}{{|}_{(x\left(t\right),y\left(t\right))=E_0}x\left(t\right)+{\displaystyle \frac{\partial f_2(x\left(t\right),y\left(t\right))}{\partial y\left(t\right)}}|}_{(x\left(t\right),y\left(t\right))=E_0}y\left(t\right).\hfill \end{array}\right.$$

(58)

Straightforward calculations yield the following:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial f_1(x\left(t\right),y\left(t\right))}{\partial x\left(t\right)}}{|}_{(x\left(t\right),y\left(t\right))=E_0}\hfill \\ \hfill & ={\displaystyle \frac{\beta [\frac{\mu }{\delta }-2x\left(t\right)-y\left(t\right)]\{1+\sigma [x\left(t\right)+y\left(t\right)]\}-\beta \sigma [\frac{\mu }{\delta }-x\left(t\right)-y\left(t\right)]x\left(t\right)}{{\{1+\sigma [x\left(t\right)+y\left(t\right)]\}}^2}}{|}_{(x\left(t\right),y\left(t\right))=E_0}\hfill \\ \hfill & -(\eta +\delta )\hfill \\ \hfill & ={\displaystyle \frac{\beta \mu }{\delta }}-(\eta +\delta )=(\eta +\delta )(R_1-1),\hfill \end{array}$$

(59)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial f_1(x\left(t\right),y\left(t\right))}{\partial y\left(t\right)}}{|}_{(x\left(t\right),y\left(t\right))=E_0}\hfill \\ \hfill & ={\displaystyle \frac{-\beta x\left(t\right)\{1+\sigma [x\left(t\right)+y\left(t\right)]\}-\beta \sigma [\frac{\mu }{\delta }-x\left(t\right)-y\left(t\right)]x\left(t\right)}{{\{1+\sigma [x\left(t\right)+y\left(t\right)]\}}^2}}{|}_{(x\left(t\right),y\left(t\right))=E_0}=0,\hfill \end{array}$$

(60)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial f_2(x\left(t\right),y\left(t\right))}{\partial x\left(t\right)}}{|}_{(x\left(t\right),y\left(t\right))=E_0}\hfill \\ \hfill & ={\displaystyle \frac{-\beta y\left(t\right)\{1+\sigma [x\left(t\right)+y\left(t\right)]\}-\beta \sigma [\frac{\mu }{\delta }-x\left(t\right)-y\left(t\right)]y\left(t\right)}{{\{1+\sigma [x\left(t\right)+y\left(t\right)]\}}^2}}{|}_{(x\left(t\right),y\left(t\right))=E_0}+\eta =\eta ,\hfill \end{array}$$

(61)

and

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial f_2(x\left(t\right),y\left(t\right))}{\partial y\left(t\right)}}{|}_{(x\left(t\right),y\left(t\right))=E_0}\hfill \\ \hfill & ={\displaystyle \frac{\beta [\frac{\mu }{\delta }-x\left(t\right)-2y\left(t\right)]\{1+\sigma [x\left(t\right)+y\left(t\right)]\}-\beta \sigma [\frac{\mu }{\delta }-x\left(t\right)-y\left(t\right)]y\left(t\right)}{{\{1+\sigma [x\left(t\right)+y\left(t\right)]\}}^2}}{|}_{(x\left(t\right),y\left(t\right))=E_0}\hfill \\ \hfill & -(\gamma +\delta )\hfill \\ \hfill & ={\displaystyle \frac{\beta \mu }{\delta }}-(\gamma +\delta )=(\gamma +\delta )(R_1-1).\hfill \end{array}$$

(62)

Hence, the linearized system of the model (28) at $E_0$ is as follows:

$$\left\{\begin{array}{cc}\hfill D^{\alpha }x\left(t\right)& =(\eta +\delta )(R_1-1)x\left(t\right),t\ge 0,\hfill \\ \hfill D^{\alpha }y\left(t\right)& =\eta x\left(t\right)+(\gamma +\delta )(R_2-1)y\left(t\right),t\ge 0.\hfill \end{array}\right.$$

(63)

The corresponding characteristic equation is as follows:

$$[\lambda -(\eta +\delta )(R_1-1)][\lambda -(\gamma +\delta )(R_2-1)]=0.$$

(64)

Theorem 3.

The following assertions hold.

(A1) 

If $R_0<1$, then $E_0$ is locally asymptotically stable.

(A2) 

If $R_0>1$, then $E_0$ is unstable.

Proof of Theorem 3.

Equation (59) admits the following two roots:

$${\lambda }_1=(\eta +\delta )(R_1-1),{\lambda }_2=(\gamma +\delta )(R_2-1).$$

(65)

In the case where $R_0<1$ (equivalently, $R_1<1$, $R_2<1$), it follows that ${\lambda }_1$ and ${\lambda }_2$ are negative numbers. So, $arg\left({\lambda }_1\right)=\pi$, $arg\left({\lambda }_2\right)=\pi$. As $0<\alpha <1$, it follows that:

$$|arg\left({\lambda }_1\right)|=\pi >{\displaystyle \frac{\alpha \pi }{2}},|arg\left({\lambda }_2\right)|=\pi >{\displaystyle \frac{\alpha \pi }{2}}.$$

(66)

Hence, it follows from Lemma 2 that $E_0$ is locally asymptotically stable.

In the case where $R_0>1$ (equivalently, $R_1>1$ or $R_2>1$), it follows that either

$$|arg\left({\lambda }_1\right)|=0<{\displaystyle \frac{\alpha \pi }{2}}.$$

(67)

or

$$|arg\left({\lambda }_2\right)|=0<{\displaystyle \frac{\alpha \pi }{2}}.$$

(68)

Hence, it follows from Lemma 2 that $E_0$ is unstable. □

Remark 5.

According to Theorem 3, the computer virus locally tends to extinction if $R_0<1$, whereas the virus does not tend to extinction if $R_0>1$.

Theorem 4.

If ${\displaystyle \frac{\beta \mu }{\delta }}\le \delta$, then $E_0$ is globally attracting.

Proof of Theorem 4.

Consider the following positive definite function:

$$U\left(t\right)=L\left(t\right)+B\left(t\right).$$

(69)

It follows that:

$$\begin{array}{cc}\hfill & D^{\alpha }U\left(t\right)=D^{\alpha }L\left(t\right)+D^{\alpha }B\left(t\right)\hfill \\ \hfill & ={\displaystyle \frac{\beta [\frac{\mu }{\delta }-L\left(t\right)-B\left(t\right)]L\left(t\right)}{1+\sigma \left[L\right(t)+B(t\left)\right]}}-\alpha L\left(t\right)-\delta L\left(t\right)\hfill \\ \hfill & +{\displaystyle \frac{\beta [\frac{\mu }{\delta }-L\left(t\right)-B\left(t\right)]B\left(t\right)}{1+\sigma \left[L\right(t)+B(t\left)\right]}}+\alpha L\left(t\right)-\gamma B\left(t\right)-\delta B\left(t\right)\hfill \\ \hfill & \le {\displaystyle \frac{\beta [\frac{\mu }{\delta }-L\left(t\right)-B\left(t\right)][L\left(t\right)+B\left(t\right)]}{1+\sigma \left[L\right(t)+B(t\left)\right]}}-\delta [L\left(t\right)+B\left(t\right)]\hfill \\ \hfill & ={\displaystyle \frac{\left\{(\frac{\beta \mu }{\delta }-\delta )-(\beta +\delta \sigma )[L\left(t\right)+B\left(t\right)]\right\}[L\left(t\right)+B\left(t\right)]}{1+\sigma \left[L\right(t)+B(t\left)\right]}}\le 0.\hfill \end{array}$$

(70)

Moreover, $D^{\alpha }U\left(t\right)=0$ if and only if $L\left(t\right)=B\left(t\right)=0$. It follows from LaSalle’s invariance principle [38] that $E_0$ is globally attracting. □

Combining Theorems 3 and 4 yields the following.

Theorem 5.

If ${\displaystyle \frac{\beta \mu }{\delta }}\le \delta$, then $E_0$ is globally asymptotically stable.

Remark 6.

According to Theorem 5, the computer virus globally tends to extinction if ${\displaystyle \frac{\beta \mu }{\delta }}\le \delta$.

8. Asymptotic Stability of the Equilibrium ${\mathit{E}}_{\mathbf{1}}$

It follows from Theorem 2 that model (23) admits a 0+ virus–endemic equilibrium if and only if $R_2>1$. In this case, the unique 0+ virus–endemic equilibrium is $E_1=(0,B_1)$, $B_1={\displaystyle \frac{(\gamma +\delta )(R_2-1)}{\beta +(\gamma +\delta )\sigma }}$.

The linearized system of the model (23) at $E_1$ is as follows:

$$\left\{\begin{array}{cc}\hfill D^{\alpha }x\left(t\right)& ={\displaystyle \frac{\partial f_1(x\left(t\right),y\left(t\right))}{\partial x\left(t\right)}}{{|}_{(x\left(t\right),y\left(t\right))=E_1}x\left(t\right)+{\displaystyle \frac{\partial f_1(x\left(t\right),y\left(t\right))}{\partial y\left(t\right)}}|}_{(x\left(t\right),y\left(t\right))=E_1}y\left(t\right),\hfill \\ \hfill D^{\alpha }y\left(t\right)& ={\displaystyle \frac{\partial f_2(x\left(t\right),y\left(t\right))}{\partial x\left(t\right)}}{{|}_{(x\left(t\right),y\left(t\right))=E_1}x\left(t\right)+{\displaystyle \frac{\partial f_2(x\left(t\right),y\left(t\right))}{\partial y\left(t\right)}}|}_{(x\left(t\right),y\left(t\right))=E_1}y\left(t\right).\hfill \end{array}\right.$$

(71)

Notice that Equation (41) implies ${\displaystyle \frac{\beta (\frac{\mu }{\delta }-B_1)}{1+\sigma B_1}}=\gamma +\delta$. Straightforward calculations lead to the following:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial f_1(x\left(t\right),y\left(t\right))}{\partial x\left(t\right)}}{|}_{(x\left(t\right),y\left(t\right))=E_1}\hfill \\ \hfill & ={\displaystyle \frac{\beta [\frac{\mu }{\delta }-2x\left(t\right)-y\left(t\right)]\{1+\sigma [x\left(t\right)+y\left(t\right)]\}-\beta \sigma [\frac{\mu }{\delta }-x\left(t\right)-y\left(t\right)]x\left(t\right)}{{\{1+\sigma [x\left(t\right)+y\left(t\right)]\}}^2}}{|}_{(x\left(t\right),y\left(t\right))=E_1}\hfill \\ \hfill & -(\eta +\delta )\hfill \\ \hfill & ={\displaystyle \frac{\beta (\frac{\mu }{\delta }-B_1)}{1+\sigma B_1}}-(\eta +\delta )=\gamma -\eta ,\hfill \end{array}$$

(72)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial f_1(x\left(t\right),y\left(t\right))}{\partial y\left(t\right)}}{|}_{(x\left(t\right),y\left(t\right))=E_1}\hfill \\ \hfill & ={\displaystyle \frac{-\beta x\left(t\right)\{1+\sigma [x\left(t\right)+y\left(t\right)]\}-\beta \sigma [\frac{\mu }{\delta }-x\left(t\right)-y\left(t\right)]x\left(t\right)}{{\{1+\sigma [x\left(t\right)+y\left(t\right)]\}}^2}}{|}_{(x\left(t\right),y\left(t\right))=E_1}=0,\hfill \end{array}$$

(73)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial f_2(x\left(t\right),y\left(t\right))}{\partial x\left(t\right)}}{|}_{(x\left(t\right),y\left(t\right))=E_1}\hfill \\ \hfill & ={\displaystyle \frac{-\beta y\left(t\right)\{1+\sigma [x\left(t\right)+y\left(t\right)]\}-\beta \sigma [\frac{\mu }{\delta }-x\left(t\right)-y\left(t\right)]y\left(t\right)}{{\{1+\sigma [x\left(t\right)+y\left(t\right)]\}}^2}}{|}_{(x\left(t\right),y\left(t\right))=E_1}+\eta ,\hfill \\ \hfill & =\eta -{\displaystyle \frac{\beta B_1(1+\frac{\mu \sigma }{\delta })}{{(1+\sigma B_1)}^2}}=M_1,\hfill \end{array}$$

(74)

and

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial f_2(x\left(t\right),y\left(t\right))}{\partial y\left(t\right)}}{|}_{(x\left(t\right),y\left(t\right))=E_1}\hfill \\ \hfill & ={\displaystyle \frac{\beta [\frac{\mu }{\delta }-x\left(t\right)-2y\left(t\right)]\{1+\sigma [x\left(t\right)+y\left(t\right)]\}-\beta \sigma [\frac{\mu }{\delta }-x\left(t\right)-y\left(t\right)]y\left(t\right)}{{\{1+\sigma [x\left(t\right)+y\left(t\right)]\}}^2}}{|}_{(x\left(t\right),y\left(t\right))=E_1}\hfill \\ \hfill & -(\gamma +\delta )\hfill \\ \hfill & ={\displaystyle \frac{\beta (\frac{\mu }{\delta }-2B_1)-(\gamma +\delta )\sigma B_1}{1+\sigma B_1}}-(\gamma +\delta )\hfill \\ \hfill & =-{\displaystyle \frac{(\gamma +\delta )(R_2-1)}{1+\sigma B_1}}=M_2<0.\hfill \end{array}$$

(75)

Hence, the linearized system of the model (23) at $E_1$ is as follows:

$$\left\{\begin{array}{cc}\hfill D^{\alpha }x\left(t\right)& =(\gamma -\eta )x\left(t\right),\hfill \\ \hfill D^{\alpha }y\left(t\right)& =M_{1}x\left(t\right)+M_{2}y\left(t\right).\hfill \end{array}\right.$$

(76)

The corresponding characteristic equation is as follows:

$$(\lambda -(\gamma -\eta ))(\lambda -M_2)=0.$$

(77)

Theorem 6.

Suppose $R_2>1$. The following assertions hold.

(A1)

If $\gamma <\eta$, then $E_1$ is locally asymptotically stable.

(A2) 

If $\gamma >\eta$, then $E_1$ is unstable.

Proof of Theorem 6.

Equation (72) admits the following two roots: ${\lambda }_1=\gamma -\eta$, ${\lambda }_2=M_2<0$. So, $|arg\left({\lambda }_2\right)|=\pi >{\displaystyle \frac{\alpha \pi }{2}}$.

In the case where $\gamma <\eta$, it follows that $|arg\left({\lambda }_1\right)|=\pi >{\displaystyle \frac{\alpha \pi }{2}}$. Hence, it follows from Lemma 2 that $E_1$ is locally asymptotically stable.

In the case where $\gamma >\eta$, it follows that $|arg\left({\lambda }_1\right)|=0<{\displaystyle \frac{\alpha \pi }{2}}$. Hence, it follows from Lemma 2 that $E_1$ is unstable. □

Remark 7.

According to Theorem 6, the computer virus is endemic if $R_2>1,\gamma <\eta$.

9. Asymptotic Stability of the Equilibrium ${\mathit{E}}_{\mathbf{2}}$

It follows from Theorem 2 that model (23) admits a ++ virus–endemic equilibrium if and only if $R_1>1$, $\gamma >\eta$. In this case, the unique ++ virus–endemic equilibrium is $E_2=(L_2,B_2)$, $L_2={\displaystyle \frac{(\gamma -\eta )(\eta +\delta )(R_1-1)}{\gamma [\beta +(\eta +\delta \left)\sigma \right]}}$, $B_2={\displaystyle \frac{\eta (\eta +\delta )(R_1-1)}{\gamma [\beta +(\eta +\delta \left)\sigma \right]}}$.

The linearized system of the model (23) at $E_2$ is as follows:

$$\left\{\begin{array}{cc}\hfill D^{\alpha }x\left(t\right)& ={\displaystyle \frac{\partial f_1(x\left(t\right),y\left(t\right))}{\partial x\left(t\right)}}{{|}_{(x\left(t\right),y\left(t\right))=E_2}x\left(t\right)+{\displaystyle \frac{\partial f_1(x\left(t\right),y\left(t\right))}{\partial y\left(t\right)}}|}_{(x\left(t\right),y\left(t\right))=E_2}y\left(t\right),\hfill \\ \hfill D^{\alpha }y\left(t\right)& ={\displaystyle \frac{\partial f_2(x\left(t\right),y\left(t\right))}{\partial x\left(t\right)}}{{|}_{(x\left(t\right),y\left(t\right))=E_2}x\left(t\right)+{\displaystyle \frac{\partial f_2(x\left(t\right),y\left(t\right))}{\partial y\left(t\right)}}|}_{(x\left(t\right),y\left(t\right))=E_2}y\left(t\right).\hfill \end{array}\right.$$

(78)

Notice that Equation (44) implies ${\displaystyle \frac{\beta (\frac{\mu }{\delta }-L_2-B_2)}{1+\sigma (L_2+B_2)}}=\eta +\delta$. Straightforward calculations yield the following:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial f_1(x\left(t\right),y\left(t\right))}{\partial x\left(t\right)}}{|}_{(x\left(t\right),y\left(t\right))=E_2}\hfill \\ \hfill & ={\displaystyle \frac{\beta [\frac{\mu }{\delta }-2x\left(t\right)-y\left(t\right)]\{1+\sigma [x\left(t\right)+y\left(t\right)]\}-\beta \sigma [\frac{\mu }{\delta }-x\left(t\right)-y\left(t\right)]x\left(t\right)}{{\{1+\sigma [x\left(t\right)+y\left(t\right)]\}}^2}}{|}_{(x\left(t\right),y\left(t\right))=E_2}\hfill \\ \hfill & -(\eta +\delta )\hfill \\ \hfill & ={\displaystyle \frac{\beta (\frac{\mu }{\delta }-2L_2-B_2)-(\eta +\delta )\sigma L_2}{1+\sigma (L_2+B_2)}}-\eta -\delta \hfill \\ \hfill & ={\displaystyle \frac{\left(\frac{\eta }{\gamma }-1\right)[\beta +(\eta +\delta )\sigma ]}{\beta +(\eta +\delta +1)\sigma }}=M_3<0,\hfill \end{array}$$

(79)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial f_1(x\left(t\right),y\left(t\right))}{\partial y\left(t\right)}}{|}_{(x\left(t\right),y\left(t\right))=E_2}\hfill \\ \hfill & ={\displaystyle \frac{-\beta x\left(t\right)\{1+\sigma [x\left(t\right)+y\left(t\right)]\}-\beta \sigma [\frac{\mu }{\delta }-x\left(t\right)-y\left(t\right)]x\left(t\right)}{{\{1+\sigma [x\left(t\right)+y\left(t\right)]\}}^2}}{|}_{(x\left(t\right),y\left(t\right))=E_2}\hfill \\ \hfill & ={\displaystyle \frac{-\beta L_2-(\eta +\delta )\sigma L_2}{1+\sigma (L_2+B_2)}}\hfill \\ \hfill & =-{\displaystyle \frac{(\gamma -\eta )(\eta +\delta )[\beta +(\eta +\delta )\sigma ](R_1-1)}{\sigma (\eta +\delta )(R_1-1)+[\beta +(\eta +\delta )\sigma ]}}=M_4<0,\hfill \end{array}$$

(80)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial f_2(x\left(t\right),y\left(t\right))}{\partial x\left(t\right)}}{|}_{(x\left(t\right),y\left(t\right))=E_2}\hfill \\ \hfill & ={\displaystyle \frac{-\beta y\left(t\right)\{1+\sigma [x\left(t\right)+y\left(t\right)]\}-\beta \sigma [\frac{\mu }{\delta }-x\left(t\right)-y\left(t\right)]y\left(t\right)}{{\{1+\sigma [x\left(t\right)+y\left(t\right)]\}}^2}}{|}_{(x\left(t\right),y\left(t\right))=E_2}+\eta ,\hfill \\ \hfill & =\eta -{\displaystyle \frac{\beta B_2+(\eta +\delta )\sigma B_2}{1+\sigma (L_2+B_2)}}\hfill \\ \hfill & =\eta -{\displaystyle \frac{\eta (\eta +\delta )[\beta +(\eta +\delta )\sigma ](R_1-1)}{\gamma (\eta +\delta )\sigma (R_1-1)+\gamma [\beta +(\eta +\delta )\sigma ]}}=M_5,\hfill \end{array}$$

(81)

and

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial f_2(x\left(t\right),y\left(t\right))}{\partial y\left(t\right)}}{|}_{(x\left(t\right),y\left(t\right))=E_2}\hfill \\ \hfill & ={\displaystyle \frac{\beta [\frac{\mu }{\delta }-x\left(t\right)-2y\left(t\right)]\{1+\sigma [x\left(t\right)+y\left(t\right)]\}-\beta \sigma [\frac{\mu }{\delta }-x\left(t\right)-y\left(t\right)]y\left(t\right)}{{\{1+\sigma [x\left(t\right)+y\left(t\right)]\}}^2}}{|}_{(x\left(t\right),y\left(t\right))=E_2}\hfill \\ \hfill & -(\gamma +\delta )\hfill \\ \hfill & ={\displaystyle \frac{\beta (\frac{\mu }{\delta }-L_2-2B_2)-(\eta +\delta )\sigma B_2}{1+\sigma (L_2+B_2)}}-(\gamma +\delta )\hfill \\ \hfill & ={\displaystyle \frac{\frac{\beta \mu }{\delta }[\beta +(\eta +\delta )\sigma ]-[\beta (\gamma +\eta )+\eta (\eta +\delta )\sigma ](\eta +\delta )(R_1-1)}{\gamma (\eta +\delta )\sigma (R_1-1)+\gamma [\beta +(\eta +\delta )\sigma ]}}-(\gamma +\delta )=M_6.\hfill \end{array}$$

(82)

Hence, the linearized system of the model (23) at $E_2$ is as follows:

$$\left\{\begin{array}{cc}\hfill D^{\alpha }x\left(t\right)& =M_{3}x\left(t\right)+M_{4}y\left(t\right),t\ge 0,\hfill \\ \hfill D^{\alpha }y\left(t\right)& =M_{5}x\left(t\right)+M_{6}y\left(t\right),t\ge 0,\hfill \end{array}\right.$$

(83)

The corresponding characteristic equation is as follows:

$$(\lambda -M_3)(\lambda -M_6)-M_4{M}_5={\lambda }^2+M_7\lambda +M_8,$$

(84)

where

$$M_7=-M_3-M_6,M_8=M_3{M}_6-M_4{M}_5.$$

(85)

Theorem 7.

Suppose $R_1>1$, $\gamma >\eta$. Let

$${\lambda }_{1,2}={\displaystyle \frac{-M_7\pm \sqrt{M_7^2-4M_8}}{2}}$$

(86)

The following assertions hold.

(A1) 

If $|arg\left({\lambda }_1\right)|>{\displaystyle \frac{\alpha \pi }{2}}$, $|arg\left({\lambda }_2\right)|>{\displaystyle \frac{\alpha \pi }{2}}$, then $E_2$ is locally asymptotically stable.

(A2) 

If $|arg\left({\lambda }_1\right)|<{\displaystyle \frac{\alpha \pi }{2}}$ or $|arg\left({\lambda }_2\right)|<{\displaystyle \frac{\alpha \pi }{2}}$, then $E_2$ is unstable.

Proof of Theorem 7.

The assertions follow directly from Lemma 2. □

Remark 8.

According to Theorem 7, the computer virus is endemic if $R_1>1,\gamma >\eta ,|arg\left({\lambda }_1\right)|>{\displaystyle \frac{\alpha \pi }{2}}$, $|arg\left({\lambda }_2\right)|>{\displaystyle \frac{\alpha \pi }{2}}$.

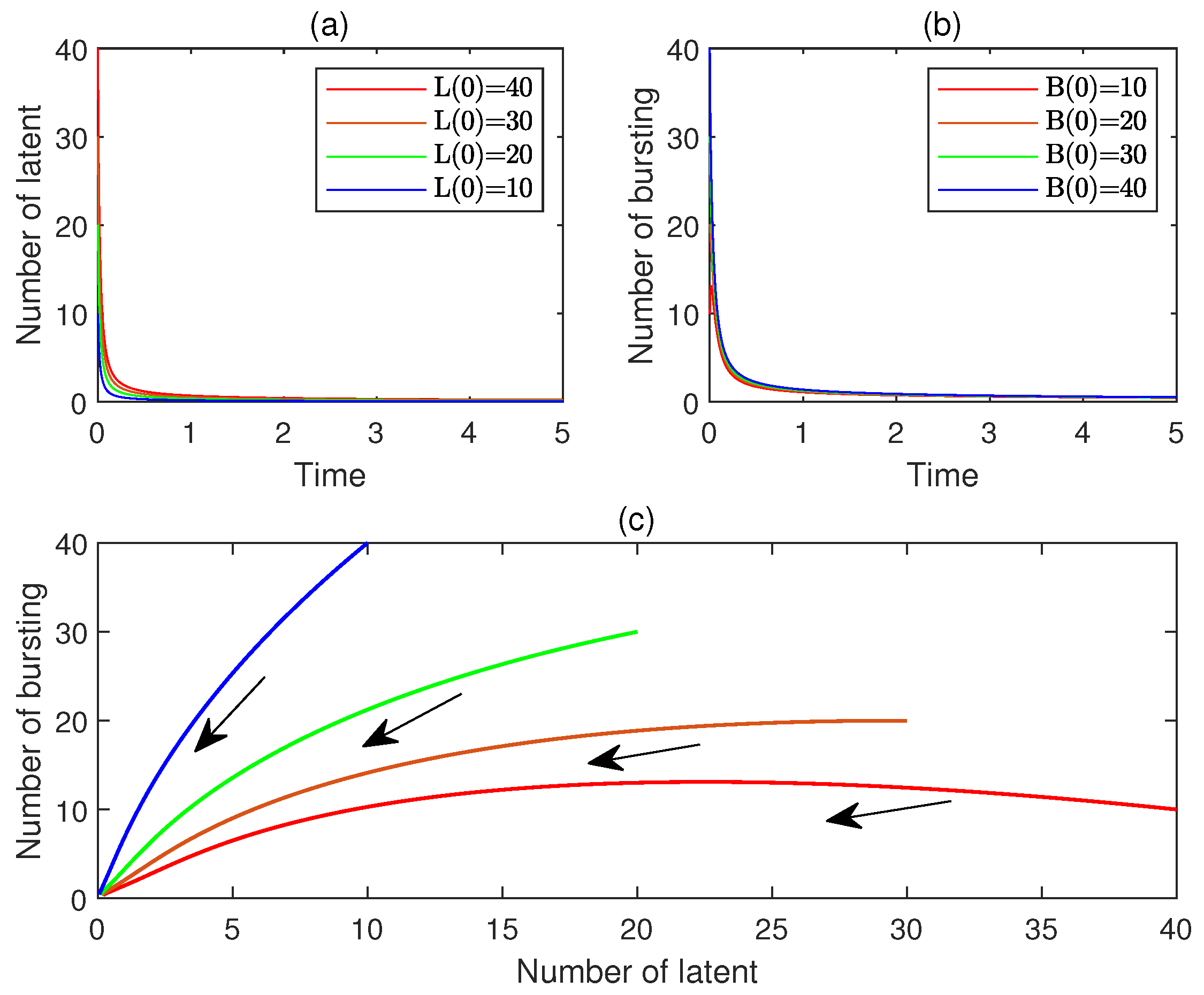
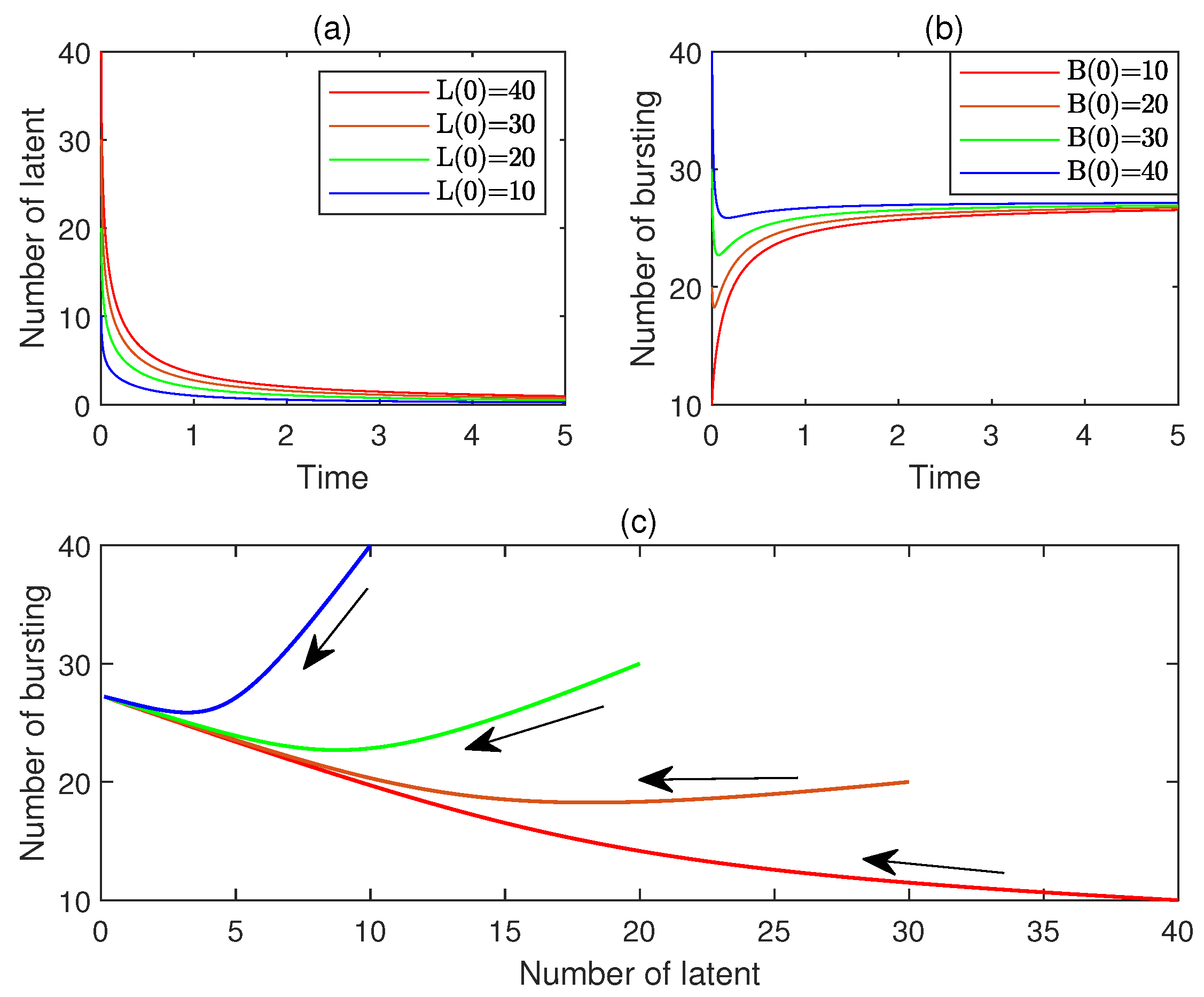
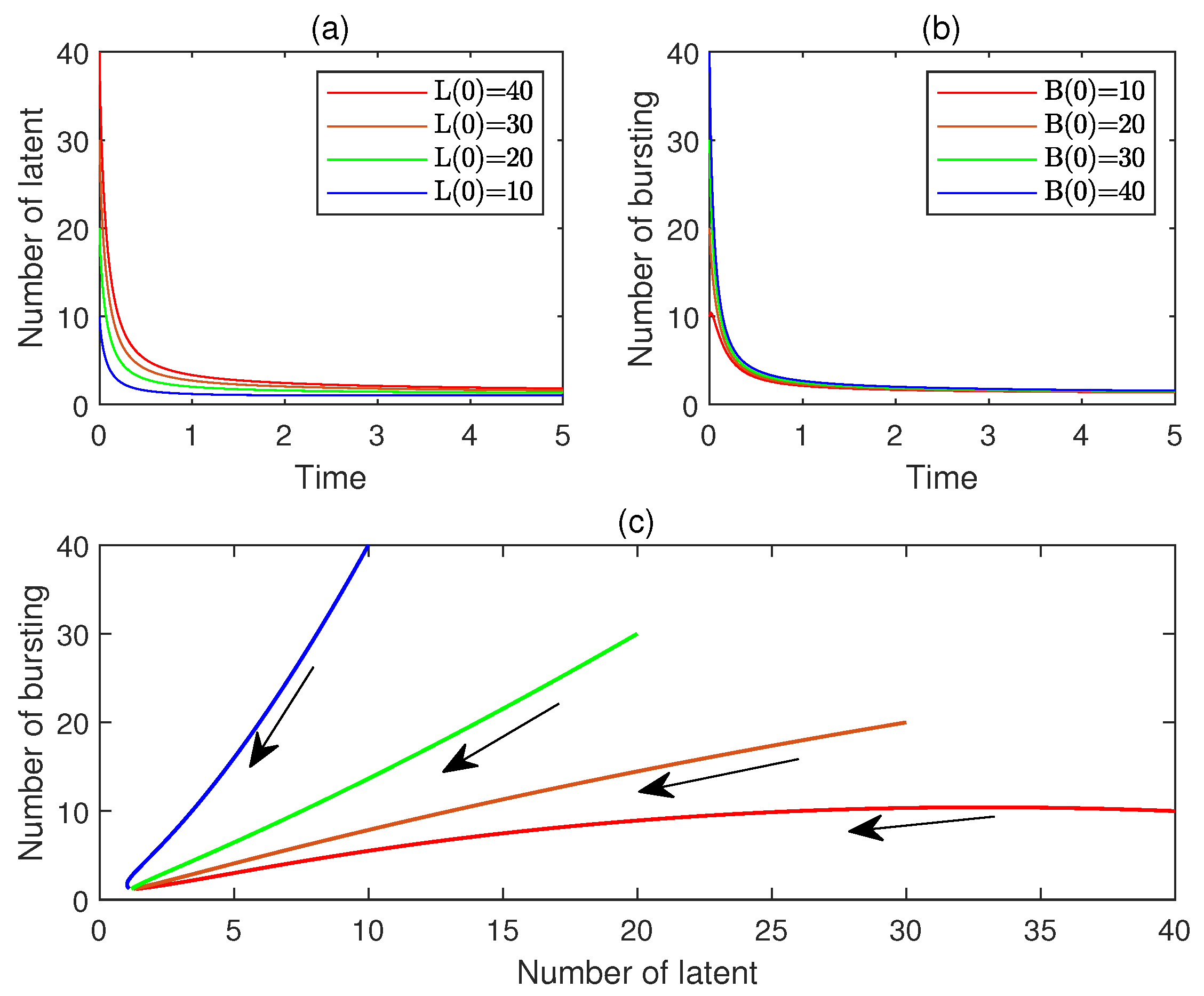
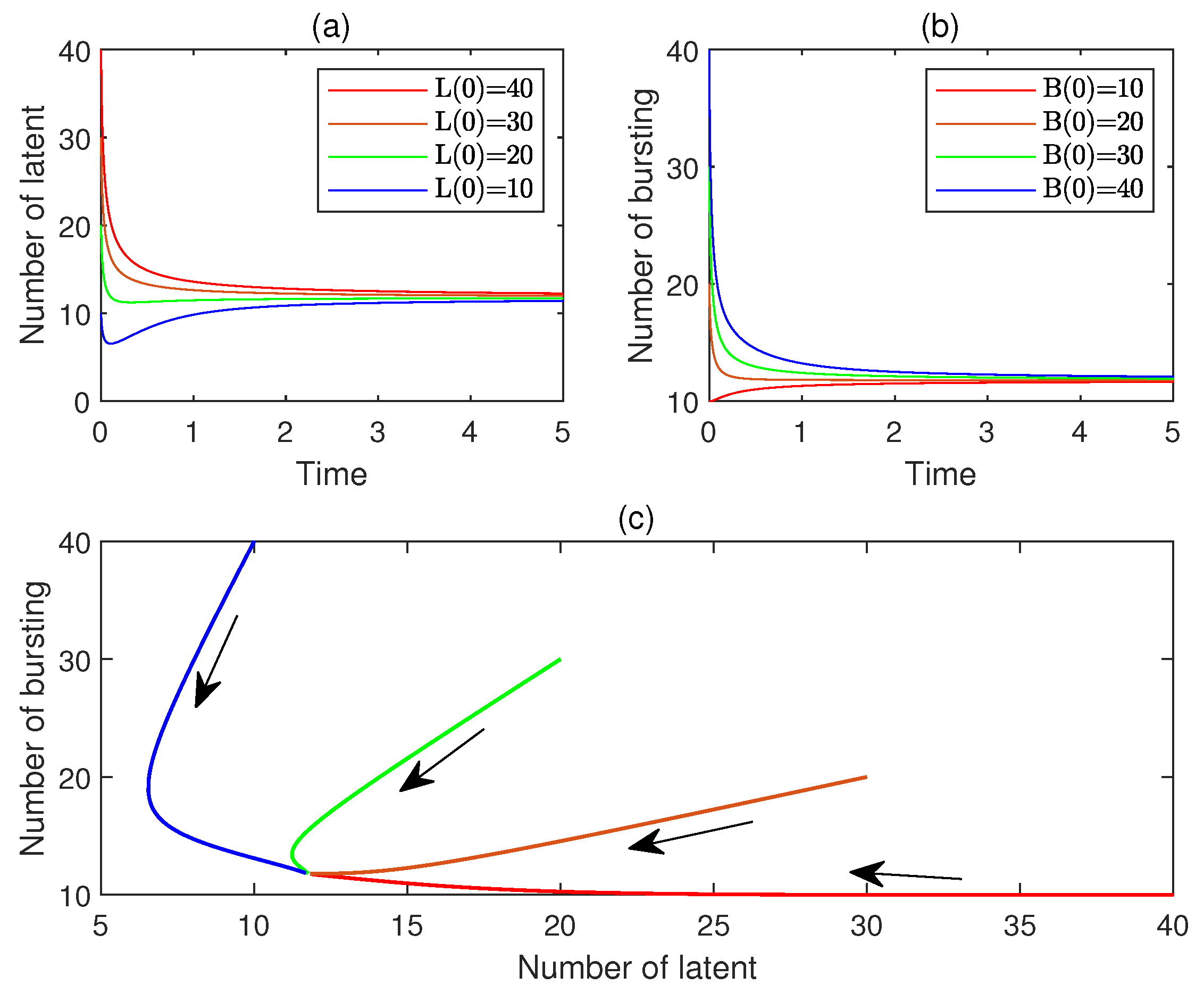
10. Numerical Simulations

The previous sections reported some theoretical findings about the asymptotic stability of model (23). This section validates these findings through numerical simulations. Here, and in what follows, model (23) is numerically solved using the classical Adams Predictor–Correction Method [39].

Experiment 1.

Consider model (23) with $\alpha =0.8$, $\mu =80$, $\delta =1$, $\beta =0.015$, $\eta =1$, $\gamma =0.5$, and $\sigma =0.6$. It is easily verified that $R_1<1$, $R_2<1$. Hence, it follows from Theorem 3 that $E_0$ is locally asymptotically stable. For each $\left(L\right(0),B(0\left)\right)\in \left\{\right(40,10),(30,20),(20,30),(10,40\left)\right\}$, Figure 1a displays the time plot of $L\left(t\right)$; Figure 1b displays the time plot of $B\left(t\right)$. Figure 1c displays the phase portrait. It is observed that $(L\left(t\right),B\left(t\right))\to E_0$, which is consistent with the predicted outcome.

Experiment 2.

Consider model (23) with $\alpha =0.8$, $\mu =40$, $\delta =1$, $\beta =0.15$, $\eta =1$, $\gamma =0.5$, and $\sigma =0.4$. It is easily verified that $R_1>1$. Hence, it follows from Theorem 3 that $E_0$ is unstable. For each $\left(L\right(0),B(0\left)\right)\in \left\{\right(40,10),(30,20),(20,30),(10,40\left)\right\}$, Figure 2a displays the time plot of $L\left(t\right)$; Figure 2b displays the time plot of $B\left(t\right)$. Figure 2c displays the phase portrait. It is observed that $(L\left(t\right),B\left(t\right))\nrightarrow E_0$, which is in line with the predicted outcome.

Experiment 3.

Consider model (23) with $\alpha =0.8$, $\mu =20$, $\delta =1$, $\beta =0.015$, $\eta =1$, $\gamma =0.5$, and $\sigma =0.6$. It is easily verified that ${\displaystyle \frac{\beta \mu }{\delta }}<\delta$. Hence, it follows from Theorem 5 that $E_0$ is globally asymptotically stable. For each $\left(L\right(0),B(0\left)\right)\in \left\{\right(40,10),(30,20),(20,30),(10,40\left)\right\}$, Figure 3a displays the time plot of $L\left(t\right)$; Figure 3b displays the time plot of $B\left(t\right)$. Figure 3c displays the phase portrait. It is observed that $(L\left(t\right),B\left(t\right))\to E_0$, which is consistent with the predicted outcome.

Experiment 4.

Consider model (23) with $\alpha =0.8$, $\mu =40$, $\delta =1$, $\beta =0.15$, $\eta =1$, $\gamma =0.5$, and $\sigma =0.01$. It is easily verified that $R_2>1$, $\gamma <\eta$, $E_1=(0,27.27)$. Hence, it follows from Theorem 6 that $E_1$ is locally asymptotically stable. For each $\left(L\right(0),B(0\left)\right)\in \left\{\right(40,10),(30,20),(20,30),(10,40\left)\right\}$, Figure 4a displays the time plot of $L\left(t\right)$. Figure 4b displays the time plot of $B\left(t\right)$. Figure 4c displays the phase portrait. It is observed that $(L\left(t\right),B\left(t\right))\to E_1$, which is in line with the predicted outcome.

Experiment 5.

Consider model (23) with $\alpha =0.8$, $\mu =40$, $\delta =1$, $\beta =0.15$, $\eta =1$, $\gamma =2$, and $\sigma =0.8$. It is easily verified that $R_2>1$, $\gamma >\eta$, $E_1=(0,1.17)$. It follows from Theorem 6 that $E_1$ is unstable. For each $\left(L\right(0),B(0\left)\right)\in \left\{\right(40,10),(30,20),(20,30),(10,40\left)\right\}$, Figure 5a displays the time plot of $L\left(t\right)$; Figure 5b displays the time plot of $B\left(t\right)$. Figure 5c displays the phase portrait. It is observed that $(L\left(t\right),B\left(t\right))\nrightarrow E_1$, which is consistent with the predicted outcome.

Experiment 6.

Consider model (23) with $\alpha =0.8$, $\mu =40$, $\delta =1$, $\beta =0.15$, $\eta =1$, $\gamma =2$, and $\sigma =0.01$. It easily verified that $R_1>1$, $\gamma >\eta$, $E_2=(11.76,11.76)$, ${\lambda }_1=-1.35$, ${\lambda }_2=-5.32$, $|arg\left({\lambda }_1\right)|>{\displaystyle \frac{\alpha \pi }{2}}$, $|arg\left({\lambda }_2\right)|>{\displaystyle \frac{\alpha \pi }{2}}$. It follows from Theorem 7 that $E_2$ is locally asymptotically stable. For each $\left(L\right(0),B(0\left)\right)\in \left\{\right(40,10),(30,20),(20,30),(10,40\left)\right\}$, Figure 6a displays the time plot of $L\left(t\right)$; Figure 6b displays the time plot of $B\left(t\right)$. Figure 6c displays the phase portrait. It is observed that $(L\left(t\right),B\left(t\right))\to E_2$, which is consistent with the predicted outcome.

Experiment 7.

Consider model (23) with $\alpha =0.8$, $\mu =80$, $\delta =0.15$, $\beta =0.8$, $\eta =0.2$, $\gamma =0.3$, and $\sigma =1$. It is easily verified that $R_1>1$, $\gamma >\eta$, $E_2=(123.57,247.14)$, ${\lambda }_1=1.91$, ${\lambda }_2=-0.48$, $|arg\left({\lambda }_1\right)|<{\displaystyle \frac{\alpha \pi }{2}}$. It follows from Theorem 7 that $E_2$ is unstable. For each $\left(L\right(0),B(0\left)\right)\in \left\{\right(40,10),(30,20),(20,30),(10,40\left)\right\}$, Figure 7a displays the time plot of $L\left(t\right)$; Figure 7b displays the time plot of $B\left(t\right)$. Figure 7c displays the phase portrait. It is observed that $(L\left(t\right),B\left(t\right))\nrightarrow E_2$, which is consistent with the predicted outcome.

11. Further Discussions

This section provides further discussions. First, the sensitivity of different model parameters to the basic reproduction number is analyzed. Second, the impact of the fractional order on virus propagation is examined. Next, the impact of the saturation index on virus spread is examined. Finally, the coupling effect of the fractional order and the saturation index on virus propagation is examined.

11.1. Sensitivity Analysis

The following theorem reveals the sensitivity of different model parameters to the basic reproduction number $R_0$.

Theorem 8.

The following assertions hold.

(A1) 

$S_{\mu }={\displaystyle \frac{\mu }{R_0}}{\displaystyle \frac{\partial R_0}{\partial \mu }}=1$.

(A2) 

$S_{\delta }={\displaystyle \frac{\delta }{R_0}}{\displaystyle \frac{\partial R_0}{\partial \delta }}=-{\displaystyle \frac{min(\eta ,\gamma )+2\delta }{min(\eta ,\gamma )+\delta }}$.

(A3) 

$S_{\beta }={\displaystyle \frac{\beta }{R_0}}{\displaystyle \frac{\partial R_0}{\partial \beta }}=1$.

(A4) 

$S_{\eta }={\displaystyle \frac{\eta }{R_0}}{\displaystyle \frac{\partial R_0}{\partial \eta }}=-{\displaystyle \frac{\eta }{\eta +\delta }}$ or 0 according as $\eta <\gamma$ or $\eta >\gamma$.

(A5) 

$S_{\gamma }={\displaystyle \frac{\gamma }{R_0}}{\displaystyle \frac{\partial R_0}{\partial \gamma }}=-{\displaystyle \frac{\gamma }{\gamma +\delta }}$ or 0 according as $\gamma <\eta$ or $\gamma >\eta$.

(A6) 

$S_{\sigma }={\displaystyle \frac{\sigma }{R_0}}{\displaystyle \frac{\partial R_0}{\partial \sigma }}=0$.

Proof of Theorem 8.

$$R_0=\left\{\begin{array}{cc}\hfill & {\displaystyle \frac{\beta \mu }{\delta (\eta +\delta )}}\mathit{if}\eta <\gamma ,\hfill \\ \hfill & {\displaystyle \frac{\beta \mu }{\delta (\gamma +\delta )}}\mathit{if}\eta >\gamma .\hfill \end{array}\right.$$

(87)

The proof of the assertion (A2):

$${\displaystyle \frac{\partial R_0}{\partial \delta }}=\left\{\begin{array}{cc}\hfill & {\displaystyle \frac{-\beta \mu (\eta +2\delta )}{{\delta }^2{(\eta +\delta )}^2}}\mathit{if}\eta <\gamma ,\hfill \\ \hfill & {\displaystyle \frac{-\beta \mu (\gamma +2\delta )}{\delta (\gamma +\delta )}}\mathit{if}\eta >\gamma .\hfill \end{array}\right.$$

(88)

$$S_{\delta }={\displaystyle \frac{\delta }{R_0}}{\displaystyle \frac{\partial R_0}{\partial \delta }}=\left\{\begin{array}{cc}\hfill & {\displaystyle \frac{\delta }{\frac{\beta \mu }{\delta (\eta +\delta )}}}{\displaystyle \frac{-\beta \mu (\eta +2\delta )}{{\delta }^2{(\eta +\delta )}^2}}=-{\displaystyle \frac{\eta +2\delta }{\eta +\delta }}\mathit{if}\eta <\gamma ,\hfill \\ \hfill & {\displaystyle \frac{\delta }{\frac{\beta \mu }{\delta (\gamma +\delta )}}}{\displaystyle \frac{-\beta \mu (\gamma +2\delta )}{\delta (\gamma +\delta )}}=-{\displaystyle \frac{\gamma +2\delta }{\gamma +\delta }}\mathit{if}\eta >\gamma ,\hfill \end{array}\right.=-{\displaystyle \frac{min(\eta ,\gamma )+2\delta }{min(\eta ,\gamma )+\delta }}.$$

(89)

The proofs of the remaining assertions are similar. □

The theorem is explained below.

(i)

The entrance rate $\mu$ has a significant positive impact on $R_0$.

(ii)

The exit rate $\delta$ has a significant negative impact on $R_0$. Furthermore, the strength of the impact strengthens with the increase in $\delta$.

(iii)

The infection force $\beta$ has a significant positive impact on $R_0$.

(iv)

In the case where $\eta <\gamma$, the burst rate $\eta$ has a significant negative impact on $R_0$. Furthermore, the strength of the impact strengthens with the increase in $\eta$.

(v)

In the case where $\eta >\gamma$, the burst rate $\eta$ has no impact on $R_0$.

(vi)

In the case where $\gamma <\eta$, the recovery rate $\gamma$ has a significant negative impact on $R_0$. Furthermore, the strength of the impact strengthens with the increase in $\gamma$.

(vii)

In the case where $\gamma >\eta$, the recovery rate $\gamma$ has no impact on $R_0$.

(viii)

The saturation index $\sigma$ has no impact on $R_0$.

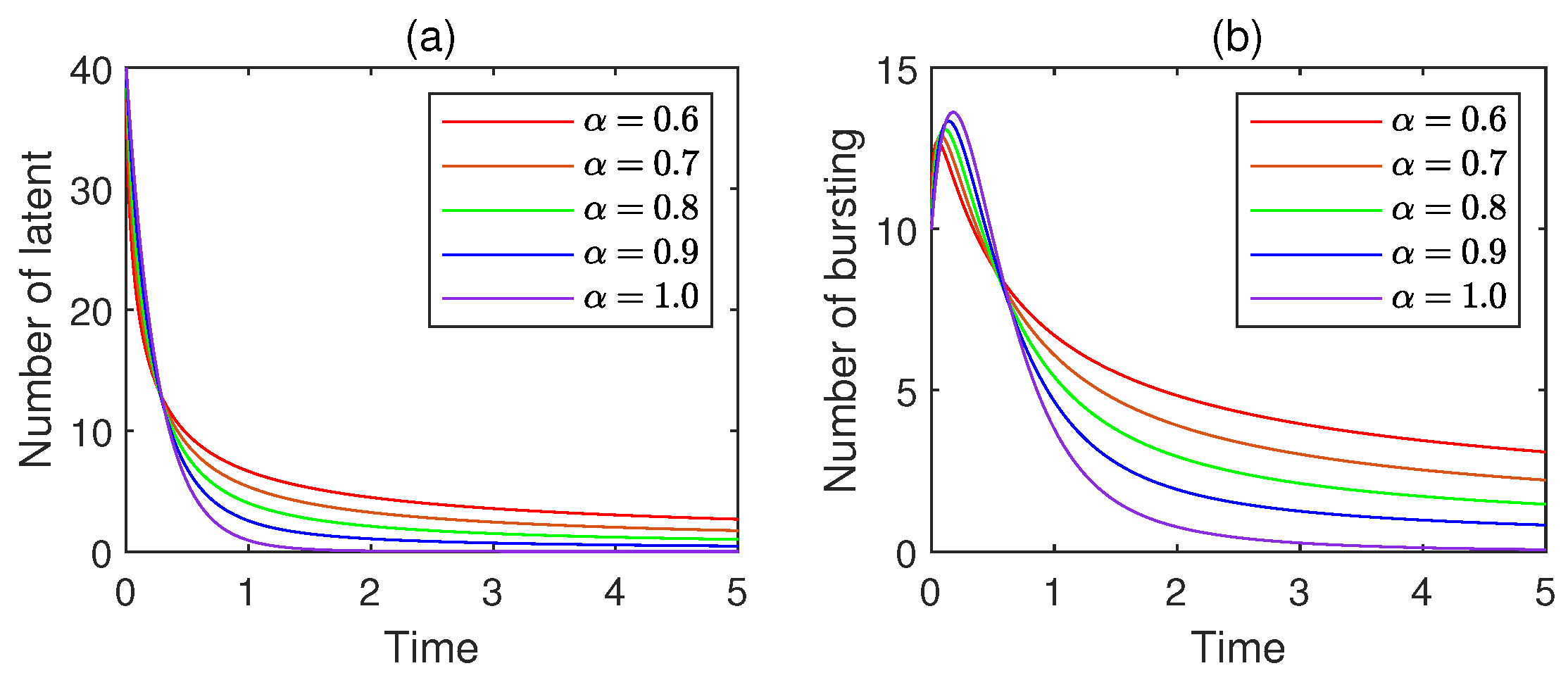
11.2. Impact of the Fractional Order

Experiment 8.

Let $\alpha \in A=\{0.6,0.7.0.8,0.9,1.0\}$, $\mu =80$, $\delta =1$, $\beta =0.015$, $\eta =1$, $\gamma =0.5$, $\sigma =0.6$, and $\left(L\right(0),B(0\left)\right)=(40,10)$. For each $\alpha \in A$, Figure 8a displays the time plot of the corresponding $L\left(t\right)$. Figure 8b displays the time plot of the corresponding $B\left(t\right)$. It is observed that with the decrease in α, $L\left(t\right)$ and $B\left(t\right)$ vary more rapidly at the early stage and vary more slowly at the subsequent stage.

From this experiment, the following conclusions are drawn.

(i)

Compared with the corresponding integer-order model, a fractional-order SLBS model shows a slower spread rate of virus. Furthermore, the smaller the fractional order, the lower the virus propagation rate would be. This reflects the memory effect of the virus and the cumulative impact of historical infection information.

(ii)

The virus does not disappear completely after a long time, maintaining a low-level residual state. This is in line with the actual situation where the latent virus persists in the network.

(iii)

With the change in fractional order, the equilibrium point of virus prevalence can be adjusted flexibly, showing a complex dynamic transition process between different states.

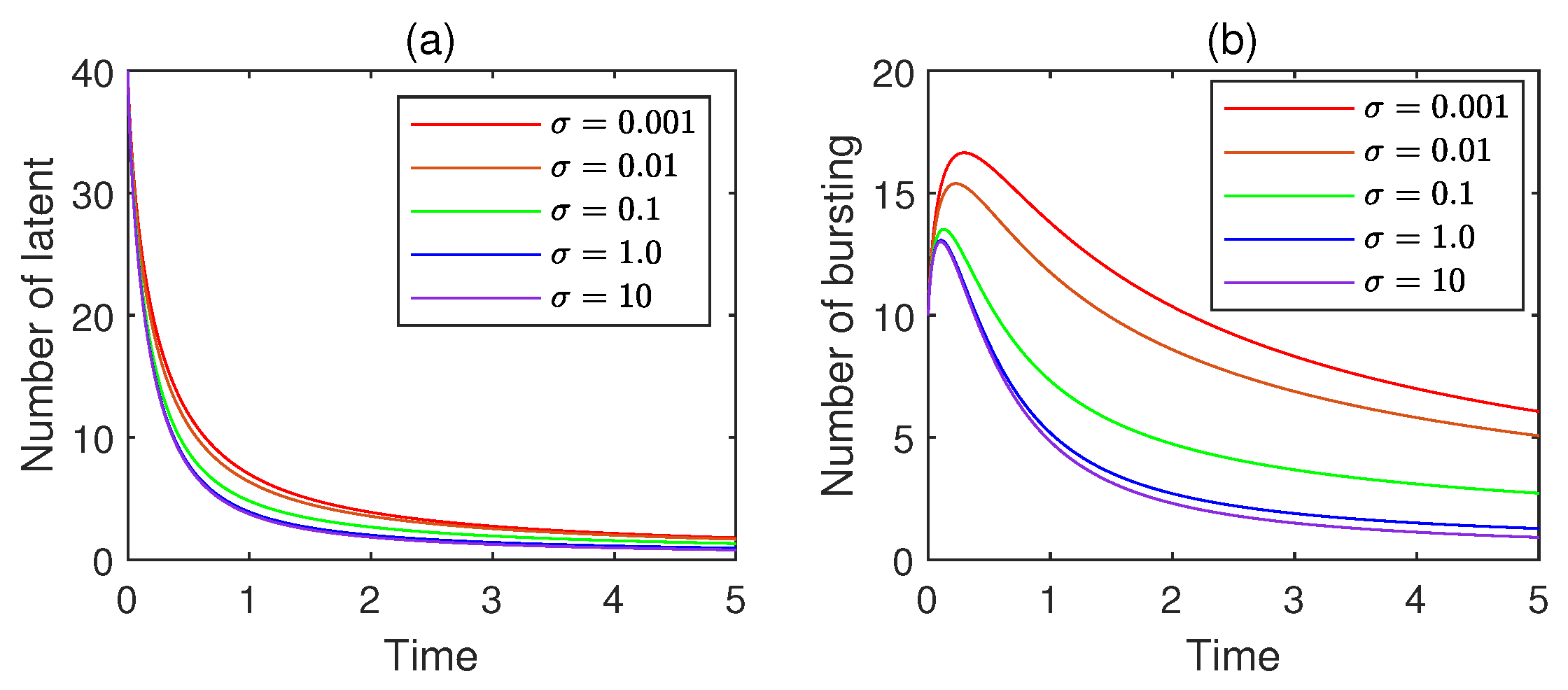
11.3. Impact of the Saturation Index

Experiment 9.

Let $\alpha =0.8$, $\mu =80$, $\delta =1$, $\beta =0.015$, $\eta =1$, $\gamma =0.5$, $\sigma \in \Sigma =\{0.001,0.01,0.1,1.0,10\}$, and $\left(L\right(0),B(0\left)\right)=(40,10)$. For each $\sigma \in \Sigma$, Figure 9a displays the time plot of the corresponding $L\left(t\right)$. Figure 9b displays the time plot of the corresponding $B\left(t\right)$. It is observed that with the increase in σ, both $L\left(t\right)$ and $B\left(t\right)$ tend to lower levels.

Experiment 10.

Let $\alpha =0.8$, $\mu =40$, $\delta =1$, $\beta =0.15$, $\eta =1$, $\gamma =2$, $\sigma \in \Sigma =\{0.001,0.01,0.1,1.0,10\}$, and $\left(L\right(0),B(0\left)\right)=(10,40)$. For each $\sigma \in \Sigma$, Figure 10a displays the time plot of the corresponding $L\left(t\right)$. Figure 10b displays the time plot of the corresponding $B\left(t\right)$. Again, it is observed that with the increase in σ, both $L\left(t\right)$ and $B\left(t\right)$ tend to lower levels.

Experiment 11.

Let $\alpha =0.8$, $\mu =80$, $\delta =0.15$, $\beta =0.15$, $\eta =0.2$, $\gamma =0.3$, $\sigma \in \Sigma =\{0.001,0.01,0.1,1.0,10\}$, and $\left(L\right(0),B(0\left)\right)=(40,10)$. For each $\sigma \in \Sigma$, Figure 11a displays the time plot of the corresponding $L\left(t\right)$. Figure 11b displays the time plot of the corresponding $B\left(t\right)$. Also, it is observed that with the increase in σ, $L\left(t\right)$ and $B\left(t\right)$ tend to lower values.

From the above three experiments, the following conclusions are drawn.

(i)

Saturation introduces a natural limit, reflecting real-world constraints like finite vulnerable devices, limited network bandwidth, or activated antivirus measures that slow spread as more devices become infected. Without saturation, the infection rate might grow indefinitely, leading to an implausible scenario where all susceptible devices become infected instantly.

(ii)

The virus spreads rapidly in the early stage when there are many susceptible devices and few barriers. However, as the number of infected devices increases, the infection rate plateaus due to saturation, causing the spread to decelerate. This results in a more realistic sigmoid curve, where the spread eventually stabilizes rather than exploding exponentially.

(iii)

By capturing the diminishing return of virus transmission, where each new infection becomes harder to achieve, this nonlinear saturation aligns the real-world behavior, making predictions of virus prevalence and spread dynamics more reliable.

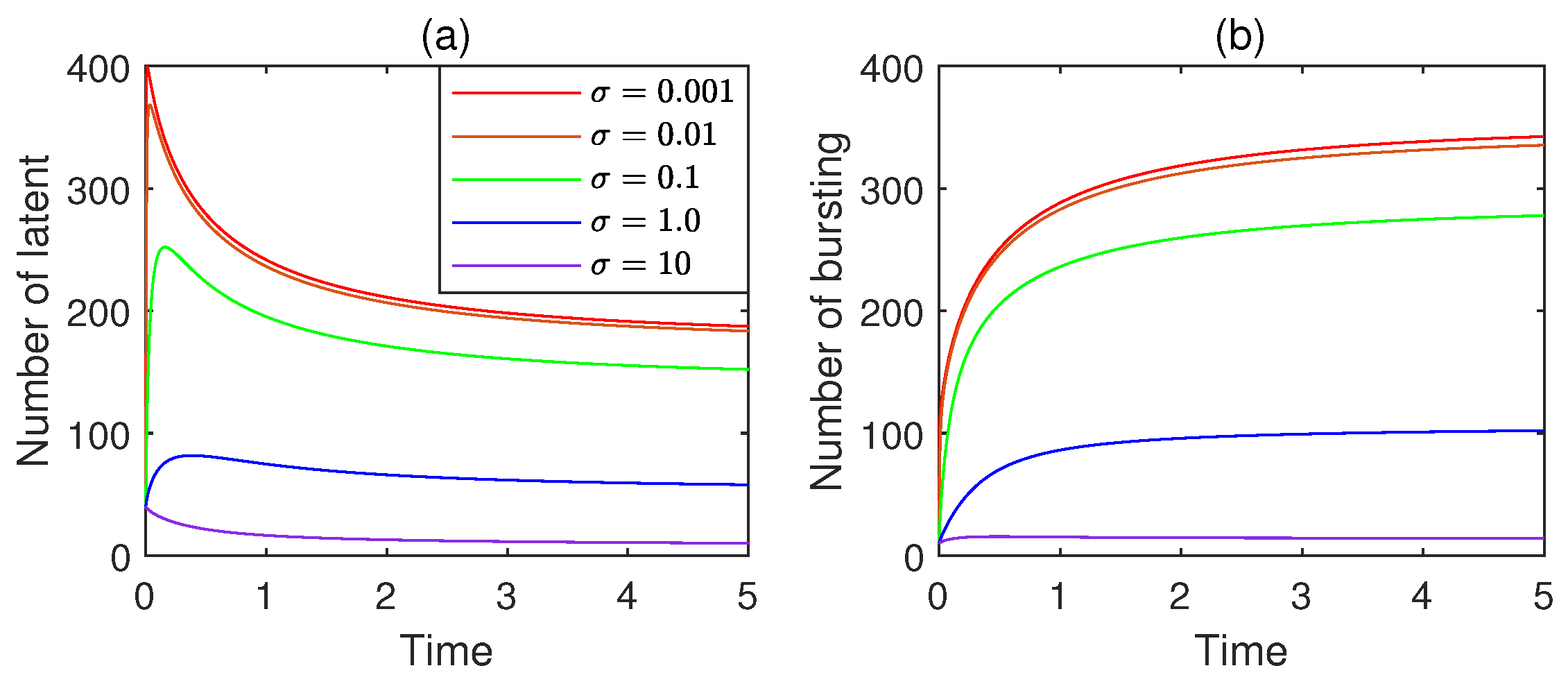
11.4. Coupling Effect of the Fractional Order and the Saturation Index

Experiment 12.

Let $\alpha \in A=\{0,6,0.7,0.8,0.9,1.0\}$, $\mu =80$, $\delta =1$, $\beta =0.015$, $\eta =1$, $\gamma =0.5$, $\sigma \in \Sigma =\{0.001,0.01,0.1,1.0,10\}$, and $\left(L\right(0),B(0\left)\right)=(40,10)$. For each combination $(\alpha ,\sigma )\in A\times \Sigma$, Figure 12a displays the time plot of the corresponding $L\left(t\right)$; Figure 12b displays the time plot of the corresponding $B\left(t\right)$. The following phenomena are observed: (1) With decreases in α, $L\left(t\right)$ and $B\left(t\right)$ vary more rapidly at the early stage and vary more slowly at the subsequent stage. (2) With the increase in α and the decrease in σ, $L\left(t\right)$ and $B\left(t\right)$ vary violently.

From this experiment, the following conclusions are drawn.

(i)

The coupling with saturation effects manifests as a dynamic interplay where the memory-dependent, non-local propagation characteristics of the fractional-order framework interact with the saturation mechanism, where the propagation rate slows or plateaus as the number of infected nodes approaches a system capacity (e.g., due to limited network resources, enhanced defense responses, or reduced susceptible nodes).

(ii)

The coupling leads to more realistic propagation dynamics, whereby the fractional-order component captures the historical influence and gradual rate changes, while the nonlinear saturation effect constrains excessive spread, reflecting real-world scenarios where propagation is limited by factors like protective measures, network load, or finite susceptible populations. Together, they yield a more accurate depiction of how viruses spread—balancing historical dependencies with the self-limiting nature of large-scale outbreaks.

12. Conclusions

In this article, a fractional computer virus propagation model with saturation effect has been suggested. All possible virus–endemic equilibria of the model have been figured out. Criteria for the local or global asymptotic stability of the virus-free equilibrium are derived. A criterion for the asymptotic stability of each possible virus–endemic equilibrium has been presented. The impact of the fractional order and the saturation index on virus propagation has been reported.

Some relevant issues are yet to be addressed. First, in reality, there exist various time delays in computer virus propagation. For example, there exists a delay from the time an infected computer becomes infected and becomes latent to the time the computer starts bursting, and there also exists a delay from the time a computer starts bursting to the time the computer is repaired. Consequently, it is worthwhile to study fractional computer virus spread models with delays [40,41,42]. Second, the fractional modeling technique of computer virus spread may be used to describe some other types of propagation phenomena, such as virus transmission [43,44,45] and rumor spreading [46,47,48]. Next, fractional virus propagation models may be adapted to the optimal control of malware infections [49,50]. Finally, fractal–fractional differential equations provide a feasible framework for characterizing the dynamical evolution of complex structures with self-similarity, irregularity, and long-term memory nature [51,52]. It is worth investigating fractal–fractional computer virus propagation models [53,54,55].