A Blind Few-Shot Learning for Multimodal-Biological Signals with Fractal Dimension Estimation
Abstract
1. Introduction
- -
- This is the first study to robustly optimize the model’s (i.e., Multi-BioSig-Net) parameters that can adapt multiple domains for a wide range of applications, including MI, ER, and SS with blind FSL, which does not need any pretraining of model.
- -
- The proposed Multi-BioSig-Net addressed the data scarcity and variability issues by considering multimodal data and the cross-correlation between them for data diversification and parameters’ generalization to mitigate the model’s underfitting on local optima due to a few training samples.
- -
- The Multi-BioSig-Net further addressed the variability issue in multifunctionality by leveraging a convolutional layer for local-equivariant and a pooling layer for contextual-invariant features to assist the multifunctionality by learning causal/non-causal and scaled-varying features to adapt all the tasks.
- -
- Fractal dimension estimation (FDE) was employed for the classification of left-hand motor imagery (LMI) and right-hand motor imagery (RMI), confirming that the proposed method can effectively extract the discriminative features for this task. In addition, our algorithm is publicly accessible via (https://github.com/dguispr/Multi-BioSig-Net.git, accessed on 1 September 2025).
2. Proposed Methods
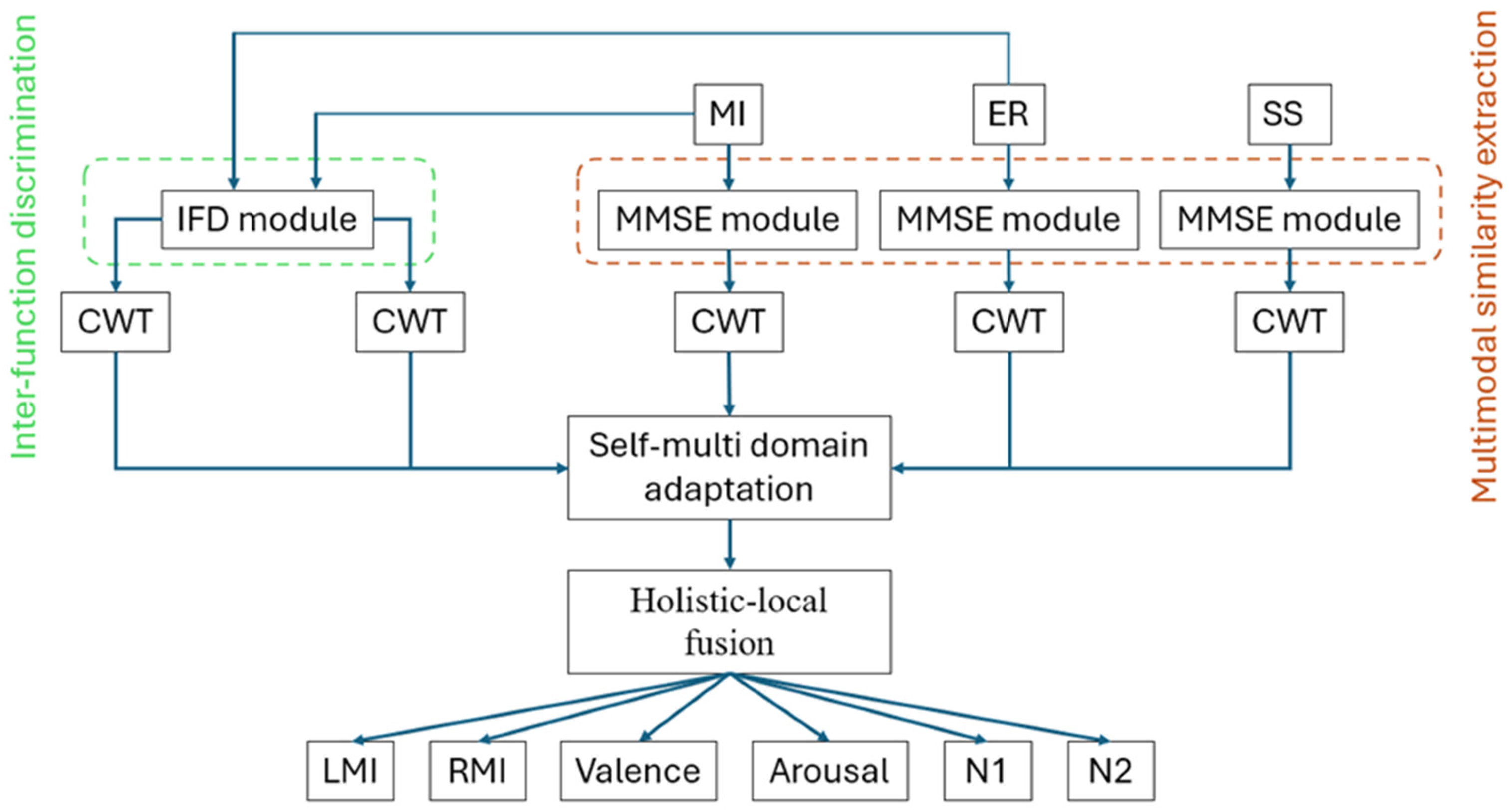
2.1. Overall Methodology
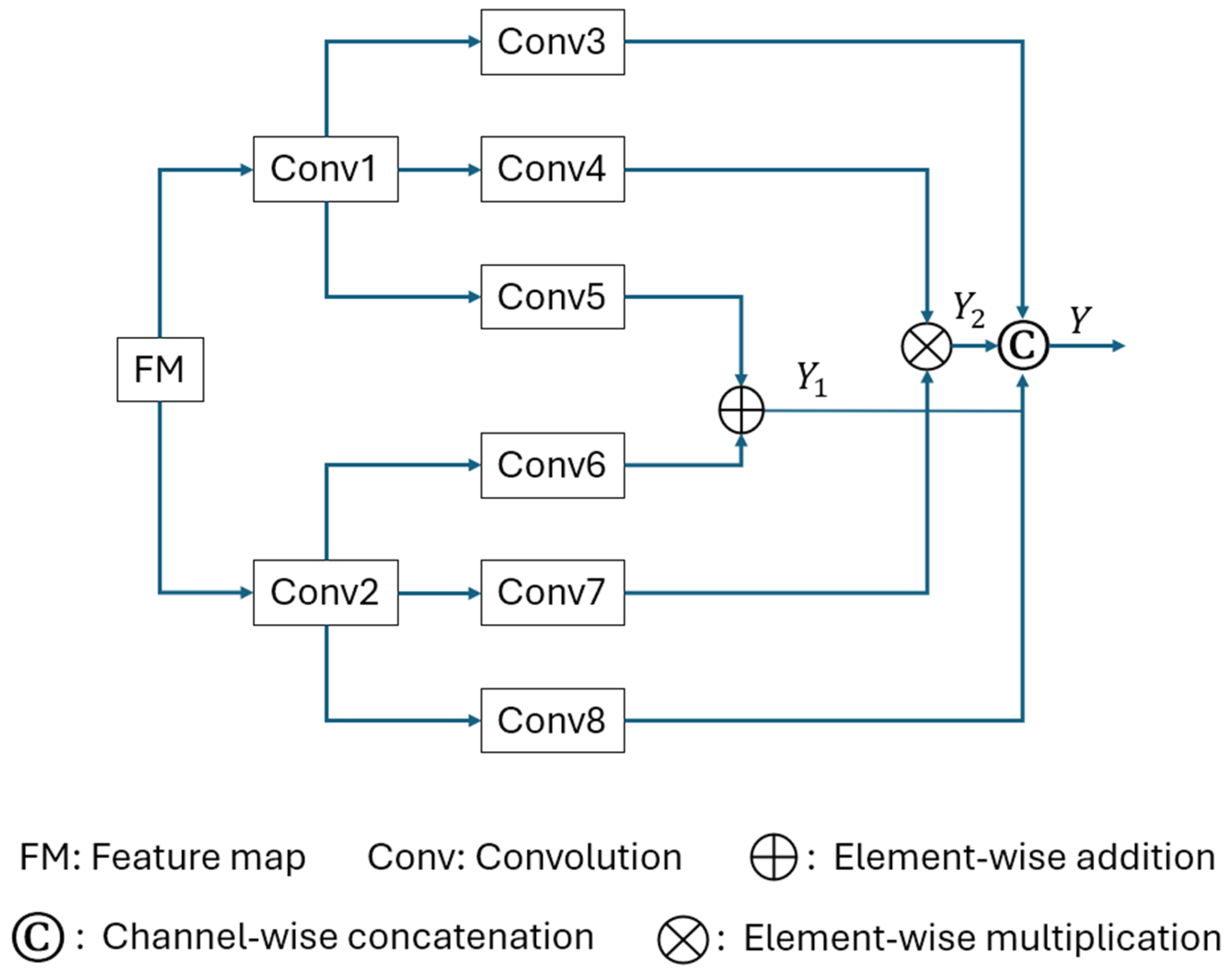
2.2. Multimodal Similarity Extractor (MMSE)
2.3. Self-Multiple Domain Adaptation (SMDA) Module
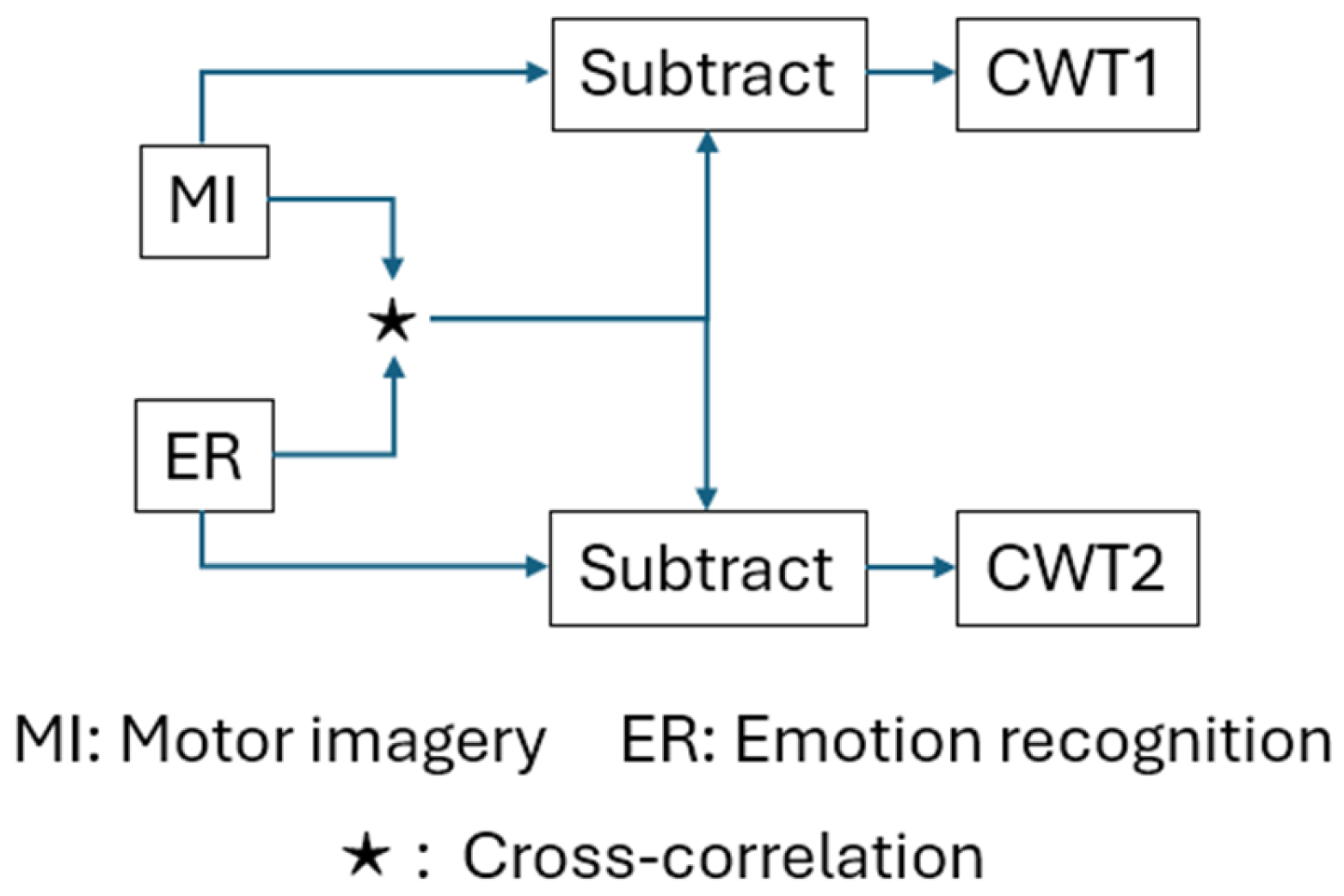
2.4. Inter-Function Discriminator (IFD)
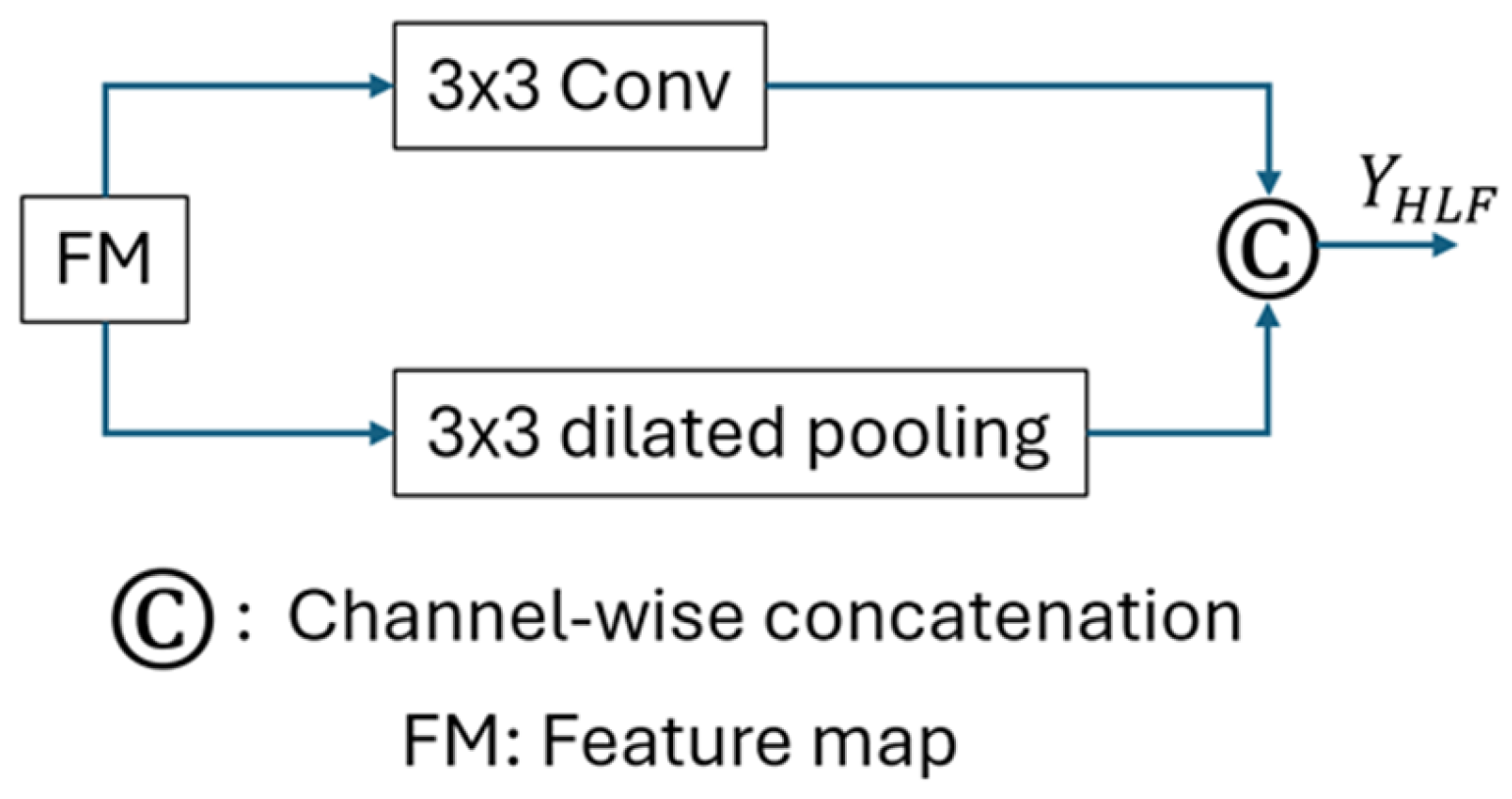
2.5. Holistic-Local Fusion (HLF) Module
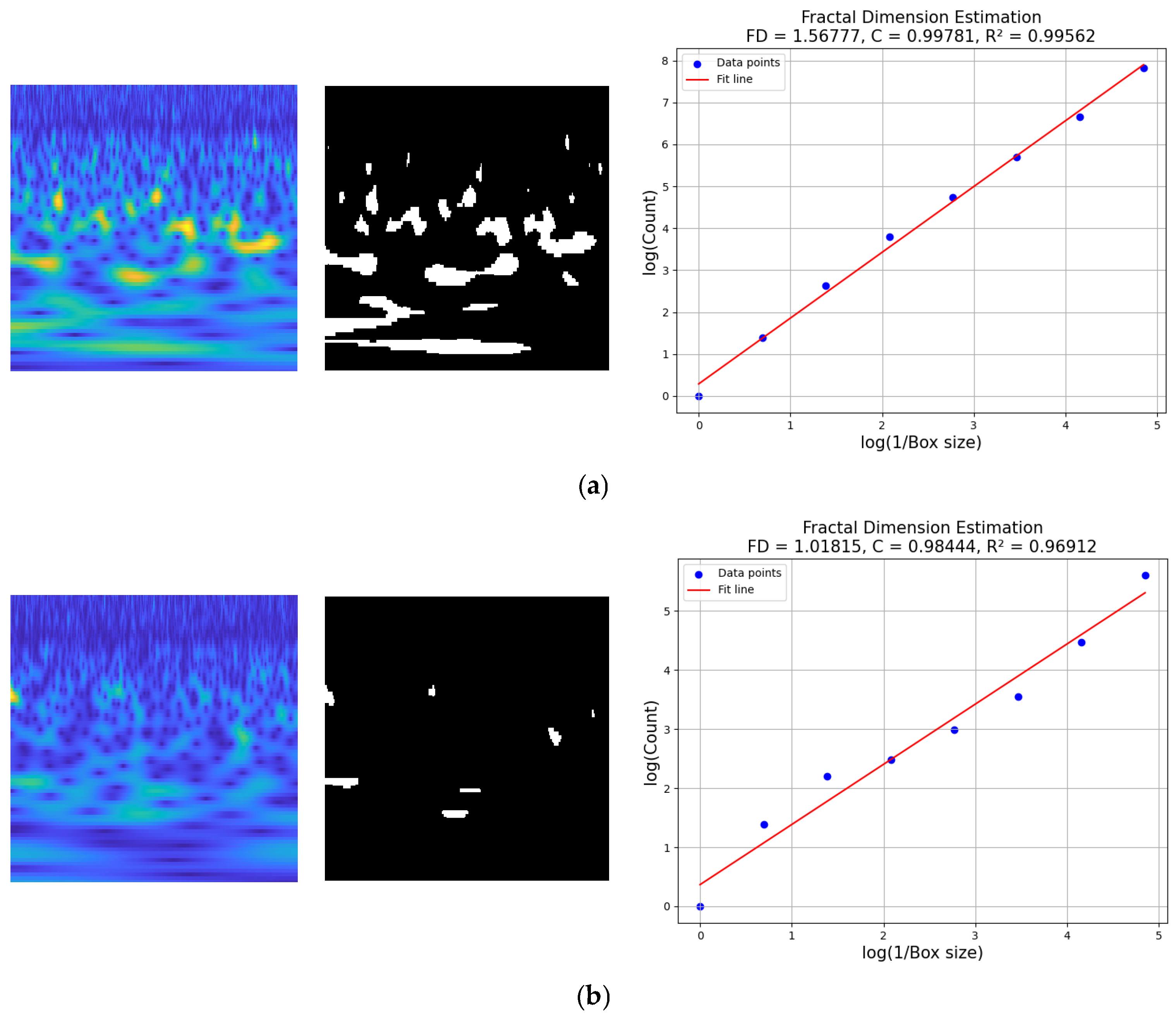
2.6. FDE
| Algorithm 1 Pseudocode for FDE and training of the proposed model |
| Input: Biscalo: Binary class activation map extracted from scalogram, MI, ER, SS. Output: FD: Fractal dimension, trained weights’ matrix (W). 1: Find the largest dimension and round it up to the closest power of two. Max_dim = max(size(Biscalo)) = 2[log2(Max_dim)] 2: Ensure the image is padded to match r if its original size is insufficient. if size(Biscalo) < size() Pad_wid=((0, −Biscalo.shape [0]), (0, −Biscalo.shape [1])) Pad_Biscalo=padding(Biscalo, Pad_wid, mode=‘constant’, constant_values=0) else Pad_Biscalo=Biscalo 3: Create an array to store the number of boxes at each scale level. n = zeros(1, +1) 4: Count the number of boxes at scale r that overlap with any active (positive) region. n[+1]=sum(Biscalo[:]) 5: While >1: a. Divide r by 2 to reduce its scale. b. Replace with the newly computed value. 6: Calculate log() and log() for every scale r. 7: Apply linear regression to the log–log data points. 8: FD corresponds to the gradient of the best-fit line in the log–log space. Return FD 9: Training the proposed model CWT=MMSE(MI, ER, SS) CWT=IFD(MI, ER) SMDA= HLF= : intermediate learnables. return W. |
3. Experiments and Results
3.1. Experimental Data
3.1.1. Brain Computer Interface (BCI) Competition IV-2a [49] (Dataset I)
3.1.2. DREAMER Dataset [51] (Dataset II)
3.1.3. Sleep-EDF Database Expanded [52] (Dataset III)
3.2. Ablation Study
3.3. Comparison with SOTA Methods
3.3.1. Based on a Single Dataset (Individual Task)
3.3.2. Based on a Combined Dataset (Multi-Task)
4. Discussion
4.1. Results of FDE
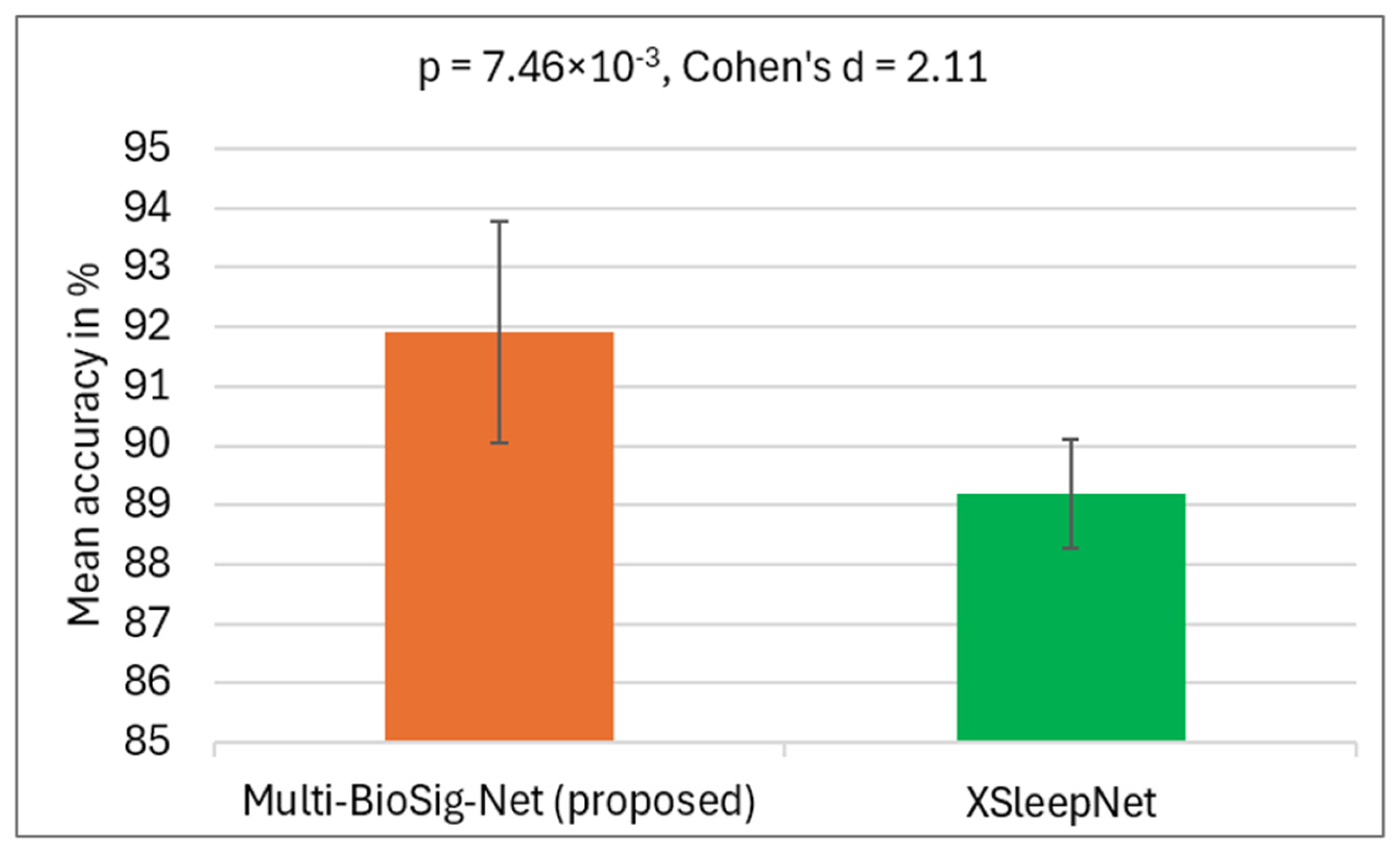
4.2. Statistical Evaluation
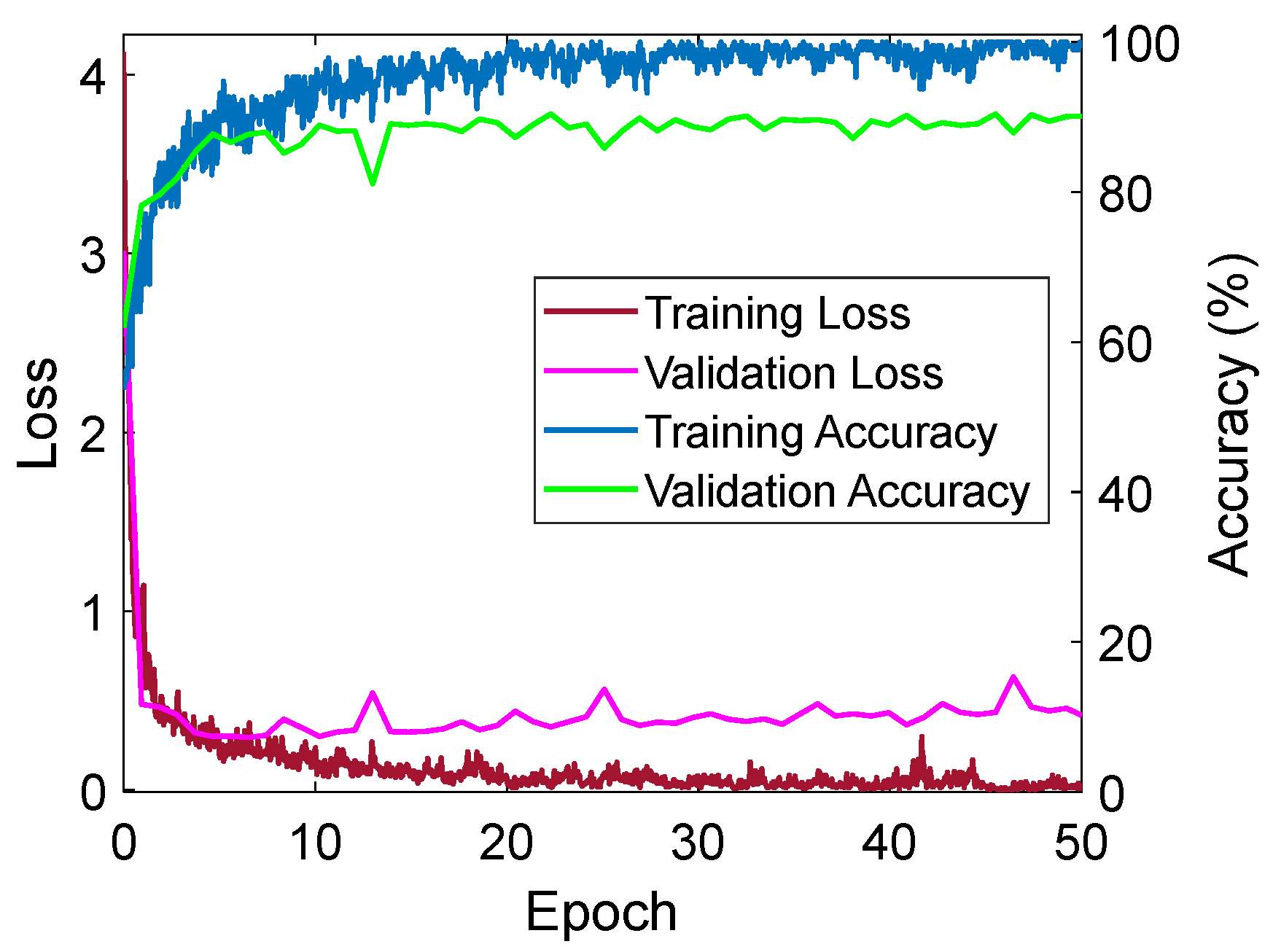
4.3. Training Loss-Accuracy Graph
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- An, S.; Kim, S.; Chikontwe, P.; Park, S.H. Dual Attention Relation Network With Fine-Tuning for Few-Shot EEG Motor Imagery Classification. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 15479–15493. [Google Scholar] [CrossRef] [PubMed]
- Ullah, N.; Mahmood, T.; Kim, S.G.; Nam, S.H.; Sultan, H.; Park, K.R. DCDA-Net: Dual-Convolutional Dual-Attention Network for Obstructive Sleep Apnea Diagnosis from Single-Lead Electrocardiograms. Eng. Appl. Artif. Intell. 2023, 123, 106451. [Google Scholar] [CrossRef]
- Zhang, T.; Ali, A.E.; Hanjalic, A.; Cesar, P. Few-Shot Learning for Fine-Grained Emotion Recognition Using Physiological Signals. IEEE Trans. Multimed. 2023, 25, 3773–3787. [Google Scholar] [CrossRef]
- Sannino, G.; De Pietro, G. A Deep Learning Approach for ECG-Based Heartbeat Classification for Arrhythmia Detection. Future Gener. Comput. Syst. 2018, 86, 446–455. [Google Scholar] [CrossRef]
- Yılmaz, B.; Asyalı, M.H.; Arıkan, E.; Yetkin, S.; Özgen, F. Sleep Stage and Obstructive Apneaic Epoch Classification Using Single-Lead ECG. BioMed. Eng. OnLine 2010, 9, 39. [Google Scholar] [CrossRef]
- Amin, S.U.; Altaheri, H.; Muhammad, G.; Abdul, W.; Alsulaiman, M. Attention-Inception and Long- Short-Term Memory-Based Electroencephalography Classification for Motor Imagery Tasks in Rehabilitation. IEEE Trans. Ind. Inform. 2022, 18, 5412–5421. [Google Scholar] [CrossRef]
- Bang, J.-S.; Lee, M.-H.; Fazli, S.; Guan, C.; Lee, S.-W. Spatio-Spectral Feature Representation for Motor Imagery Classification Using Convolutional Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 3038–3049. [Google Scholar] [CrossRef]
- Hsu, W.Y.; Cheng, Y.W. EEG-Channel-Temporal-Spectral-Attention Correlation for Motor Imagery EEG Classification. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 1659–1669. [Google Scholar] [CrossRef]
- Joshi, V.M.; Ghongade, R.B. EEG Based Emotion Detection Using Fourth Order Spectral Moment and Deep Learning. Biomed. Signal Process. Control 2021, 68, 102755. [Google Scholar] [CrossRef]
- Ozdemir, M.A.; Degirmenci, M.; Izci, E.; Akan, A. EEG-Based Emotion Recognition with Deep Convolutional Neural Networks. Biomed. Eng. Biomed. Tech. 2021, 66, 43–57. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez Aguiñaga, A.; Muñoz Delgado, L.; López-López, V.R.; Calvillo Téllez, A. EEG-Based Emotion Recognition Using Deep Learning and M3GP. Appl. Sci. 2022, 12, 2527. [Google Scholar] [CrossRef]
- Liang, X.; Tu, G.; Du, J.; Xu, R. Multi-Modal Attentive Prompt Learning for Few-Shot Emotion Recognition in Conversations. J. Artif. Intell. Res. 2024, 79, 825–863. [Google Scholar] [CrossRef]
- She, Q.; Li, C.; Tan, T.; Fang, F.; Zhang, Y. Improved Few-Shot Learning Based on Triplet Metric for Motor Imagery EEG Classification. IEEE Trans. Cogn. Dev. Syst. 2025, 17, 987–999. [Google Scholar] [CrossRef]
- Tang, M.; Zhang, Z.; He, Z.; Li, W.; Mou, X.; Du, L.; Wang, P.; Zhao, Z.; Chen, X.; Li, X.; et al. Deep Adaptation Network for Subject-Specific Sleep Stage Classification Based on a Single-Lead ECG. Biomed. Signal Process. Control 2022, 75, 103548. [Google Scholar] [CrossRef]
- Yu, J.; Duan, L.; Ji, H.; Li, J.; Pang, Z. Meta-Learning for EEG Motor Imagery Classification. Comput. Inform. 2024, 43, 735–755. [Google Scholar] [CrossRef]
- Phunruangsakao, C.; Achanccaray, D.; Hayashibe, M. Deep Adversarial Domain Adaptation With Few-Shot Learning for Motor-Imagery Brain-Computer Interface. IEEE Access 2022, 10, 57255–57265. [Google Scholar] [CrossRef]
- Chen, L.; Yu, Z.; Yang, J. SPD-CNN: A Plain CNN-Based Model Using the Symmetric Positive Definite Matrices for Cross-Subject EEG Classification with Meta-Transfer-Learning. Front. Neurorobot. 2022, 16, 958052. [Google Scholar] [CrossRef]
- Zhu, L.; Liu, Y.; Liu, R.; Peng, Y.; Cao, J.; Li, J.; Kong, W. Decoding Multi-Brain Motor Imagery From EEG Using Coupling Feature Extraction and Few-Shot Learning. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 4683–4692. [Google Scholar] [CrossRef]
- Liu, W.; Qiu, J.-L.; Zheng, W.-L.; Lu, B.-L. Comparing Recognition Performance and Robustness of Multimodal Deep Learning Models for Multimodal Emotion Recognition. IEEE Trans. Cogn. Dev. Syst. 2022, 14, 715–729. [Google Scholar] [CrossRef]
- Cheng, J.; Chen, M.; Li, C.; Liu, Y.; Song, R.; Liu, A.; Chen, X. Emotion Recognition From Multi-Channel EEG via Deep Forest. IEEE J. Biomed. Health Inform. 2021, 25, 453–464. [Google Scholar] [CrossRef]
- Cui, H.; Liu, A.; Zhang, X.; Chen, X.; Wang, K.; Chen, X. EEG-Based Emotion Recognition Using an End-to-End Regional-Asymmetric Convolutional Neural Network. Knowl.-Based Syst. 2020, 205, 106243. [Google Scholar] [CrossRef]
- Quan, J.; Li, Y.; Wang, L.; He, R.; Yang, S.; Guo, L. EEG-Based Cross-Subject Emotion Recognition Using Multi-Source Domain Transfer Learning. Biomed. Signal Process. Control 2023, 84, 104741. [Google Scholar] [CrossRef]
- Liu, Y.; Ding, Y.; Li, C.; Cheng, J.; Song, R.; Wan, F.; Chen, X. Multi-Channel EEG-Based Emotion Recognition via a Multi-Level Features Guided Capsule Network. Comput. Biol. Med. 2020, 123, 103927. [Google Scholar] [CrossRef]
- Chen, C.; Fang, H.; Yang, Y.; Zhou, Y. Model-Agnostic Meta-Learning for EEG-Based Inter-Subject Emotion Recognition. J. Neural Eng. 2025, 22, 016008. [Google Scholar] [CrossRef]
- Zheng, W.-L.; Lu, B.-L. Investigating Critical Frequency Bands and Channels for EEG-Based Emotion Recognition with Deep Neural Networks. IEEE Trans. Auton. Ment. Dev. 2015, 7, 162–175. [Google Scholar] [CrossRef]
- Lawhern, V.J.; Solon, A.J.; Waytowich, N.R.; Gordon, S.M.; Hung, C.P.; Lance, B.J. EEGNet: A Compact Convolutional Neural Network for EEG-Based Brain–Computer Interfaces. J. Neural Eng. 2018, 15, 056013. [Google Scholar] [CrossRef]
- Sangineto, E.; Zen, G.; Ricci, E.; Sebe, N. We Are Not All Equal: Personalizing Models for Facial Expression Analysis with Transductive Parameter Transfer. In Proceedings of the 22nd ACM International Conference on Multimedia, Orlando, FL, USA, 3 November 2014; pp. 357–366. [Google Scholar]
- Pan, S.J.; Tsang, I.W.; Kwok, J.T.; Yang, Q. Domain Adaptation via Transfer Component Analysis. IEEE Trans. Neural Netw. 2011, 22, 199–210. [Google Scholar] [CrossRef]
- Müller, K.-R.; Mika, S.; Tsuda, K.; Schölkopf, K. An Introduction to Kernel-Based Learning Algorithms. In Handbook of Neural Network Signal Processing; CRC Press: Boca Raton, FL, USA, 2002; ISBN 978-1-315-22041-3. [Google Scholar]
- Banluesombatkul, N.; Ouppaphan, P.; Leelaarporn, P.; Lakhan, P.; Chaitusaney, B.; Jaimchariyatam, N.; Chuangsuwanich, E.; Chen, W.; Phan, H.; Dilokthanakul, N.; et al. MetaSleepLearner: A Pilot Study on Fast Adaptation of Bio-Signals-Based Sleep Stage Classifier to New Individual Subject Using Meta-Learning. IEEE J. Biomed. Health Inform. 2021, 25, 1949–1963. [Google Scholar] [CrossRef]
- Mousavi, S.; Afghah, F.; Acharya, U.R. SleepEEGNet: Automated Sleep Stage Scoring with Sequence to Sequence Deep Learning Approach. PLoS ONE 2019, 14, e0216456. [Google Scholar] [CrossRef]
- Supratak, A.; Dong, H.; Wu, C.; Guo, Y. DeepSleepNet: A Model for Automatic Sleep Stage Scoring Based on Raw Single-Channel EEG. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 1998–2008. [Google Scholar] [CrossRef]
- Fiorillo, L.; Favaro, P.; Faraci, F.D. DeepSleepNet-Lite: A Simplified Automatic Sleep Stage Scoring Model With Uncertainty Estimates. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 2076–2085. [Google Scholar] [CrossRef] [PubMed]
- Eldele, E.; Chen, Z.; Liu, C.; Wu, M.; Kwoh, C.-K.; Li, X.; Guan, C. An Attention-Based Deep Learning Approach for Sleep Stage Classification With Single-Channel EEG. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 809–818. [Google Scholar] [CrossRef] [PubMed]
- Phan, H.; Chén, O.Y.; Tran, M.C.; Koch, P.; Mertins, A.; De Vos, M. XSleepNet: Multi-View Sequential Model for Automatic Sleep Staging. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 5903–5915. [Google Scholar] [CrossRef] [PubMed]
- Khalili, E.; Mohammadzadeh Asl, B. Automatic Sleep Stage Classification Using Temporal Convolutional Neural Network and New Data Augmentation Technique from Raw Single-Channel EEG. Comput. Methods Programs Biomed. 2021, 204, 106063. [Google Scholar] [CrossRef]
- Perslev, M.; Darkner, S.; Kempfner, L.; Nikolic, M.; Jennum, P.J.; Igel, C. U-Sleep: Resilient High-Frequency Sleep Staging. NPJ Digit. Med. 2021, 4, 72. [Google Scholar] [CrossRef]
- Goshtasbi, N.; Boostani, R.; Sanei, S. SleepFCN: A Fully Convolutional Deep Learning Framework for Sleep Stage Classification Using Single-Channel Electroencephalograms. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 2088–2096. [Google Scholar] [CrossRef]
- Qu, W.; Wang, Z.; Hong, H.; Chi, Z.; Feng, D.D.; Grunstein, R.; Gordon, C. A Residual Based Attention Model for EEG Based Sleep Staging. IEEE J. Biomed. Health Inform. 2020, 24, 2833–2843. [Google Scholar] [CrossRef]
- Seo, H.; Back, S.; Lee, S.; Park, D.; Kim, T.; Lee, K. Intra- and Inter-Epoch Temporal Context Network (IITNet) Using Sub-Epoch Features for Automatic Sleep Scoring on Raw Single-Channel EEG. Biomed. Signal Process. Control 2020, 61, 102037. [Google Scholar] [CrossRef]
- Li, J.; Wu, C.; Pan, J.; Wang, F. Few-Shot EEG Sleep Staging Based on Transductive Prototype Optimization Network. Front. Neuroinform. 2023, 17, 1297874. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Brouty, X.; Garcin, M. Fractal properties; information theory, and market efficiency. Chaos Solitons Fractals 2024, 180, 114543. [Google Scholar] [CrossRef]
- Yin, J. Dynamical fractal: Theory and case study. Chaos Solitons Fractals 2023, 176, 114190. [Google Scholar] [CrossRef]
- Crownover, R.M. Introduction to Fractals and Chaos, 1st ed.; Jones & Bartlett Publisher: Burlington, MA, USA, 1995. [Google Scholar]
- Denisova, E.; Bocchi, L. Optimizing Biomedical Volume Rendering: Fractal Dimension-Based Approach for Enhanced Performance. In Proceedings of the Medical Imaging 2024: Clinical and Biomedical Imaging, San Diego, CA, USA, 2 April 2024; SPIE: Bellingham, WA, USA, 2024; Volume 12930, pp. 640–649. [Google Scholar]
- Meenakshi, M.; Gowrisankar, A. Fractal-Based Approach on Analyzing the Trends of Climate Dynamics. Int. J. Mod. Phys. B 2024, 38, 2440006. [Google Scholar] [CrossRef]
- Ruiz de Miras, J.; Li, Y.; León, A.; Arroyo, G.; López, L.; Torres, J.C.; Martín, D. Ultra-Fast Computation of Fractal Dimension for RGB Images. Pattern Anal. Applic. 2025, 28, 36. [Google Scholar] [CrossRef]
- Brunner, C.; Leeb, R.; Muller-Putz, G.R.; Schlogl, A. BCI Competition 2008—Graz Data Set A; Institute for Knowledge Discovery, Graz University of Technology: Graz, Austria. Available online: http://www.bbci.de/competition/iv/desc_2a.pdf (accessed on 29 August 2025).
- Ullah, N.; Sultan, H.; Hong, J.S.; Kim, S.G.; Akram, R.; Park, K.R. Convolutional Self-Attention with Adaptive Channel-Attention Network for Obstructive Sleep Apnea Detection Using Limited Training Data. Eng. Appl. Artif. Intell. 2025, 156, 111154. [Google Scholar] [CrossRef]
- Katsigiannis, S.; Ramzan, N. DREAMER: A Database for Emotion Recognition Through EEG and ECG Signals from Wireless Low-Cost Off-the-Shelf Devices. IEEE J. Biomed. Health Inform. 2018, 22, 98–107. [Google Scholar] [CrossRef]
- Kemp, B.; Zwinderman, A.; Tuk, B.; Kamphuisen, H.; Oberyé, J. The Sleep-EDF Database [Expanded]. PhysioNet, MIT Laboratory for Computational Physiology: Cambridge, MA, USA, 2018. [Google Scholar] [CrossRef]
- MATLAB R2024a. 2025. Available online: https://www.mathworks.com/products/matlab.html (accessed on 17 April 2025).
- GeForce GTX 1070. 2025. Available online: https://www.nvidia.com/en-gb/geforce/products/10series/geforce-gtx-1070/ (accessed on 17 April 2025).
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Schirrmeister, R.T.; Springenberg, J.T.; Fiederer, L.D.J.; Glasstetter, M.; Eggensperger, K.; Tangermann, M.; Hutter, F.; Burgard, W.; Ball, T. Deep Learning with Convolutional Neural Networks for EEG Decoding and Visualization. Hum. Brain Mapp. 2017, 38, 5391–5420. [Google Scholar] [CrossRef]
- Kashefi Amiri, H.; Zarei, M.; Daliri, M.R. Motor Imagery Electroencephalography Channel Selection Based on Deep Learning: A Shallow Convolutional Neural Network. Eng. Appl. Artif. Intell. 2024, 136, 108879. [Google Scholar] [CrossRef]
- Sorkhi, M.; Jahed-Motlagh, M.R.; Minaei-Bidgoli, B.; Daliri, M.R. Hybrid Fuzzy Deep Neural Network toward Temporal-Spatial-Frequency Features Learning of Motor Imagery Signals. Sci. Rep. 2022, 12, 22334. [Google Scholar] [CrossRef]
- Student’s t-test. 15 June 2025. Available online: https://en.wikipedia.org/w/index.php?title=Student%27s_t-test&oldid=1262286726 (accessed on 25 June 2025).
- Cohen, J. A power primer. Psychol. Bull. 1992, 112, 155–159. [Google Scholar] [CrossRef]

| Modules | MMSE | SMDA | IFD | HLF | Accuracy | |
|---|---|---|---|---|---|---|
| Data | ||||||
| 1-shot | ✓ | 65.4/64.2/67.8 | ||||
| ✓ | ✓ | 69.5/69.1/68.7 | ||||
| ✓ | ✓ | ✓ | 72.6/72.3/71.8 | |||
| ✓ | ✓ | ✓ | ✓ | 78.5/78.3/80.4 | ||
| 10-shot | ✓ | 70.3/69.6/73.2 | ||||
| ✓ | ✓ | 75.1/73.6/77.4 | ||||
| ✓ | ✓ | ✓ | 78.2/76.8/82.4 | |||
| ✓ | ✓ | ✓ | ✓ | 84.5/81.7/89.3 | ||
| Tasks | Algorithms | 1-Shot | 5-Shot | 10-Shot | 20-Shot | P | IT |
|---|---|---|---|---|---|---|---|
| MI | Meta-L MI [15] | 67.4 | 73.1 | 74.3 * | 74.4 * | 97.4 * | 42.7 * |
| FSL-DA MI [16] | 67.1* | 75.8 | 74.4 * | 74.1 * | 196.6 * | 63 * | |
| MI RelationNet [1] | 58.2 | 63.5 | 65.2 | 65.6 | 86.3 * | 42.7 * | |
| IFSL-MI [13] | 56.2 | 60.3 | 64.45 | 68.2 | - | - | |
| SPD-CNN [17] | - | 42.9 | 46.7 | - | 6.6 * | 26.5 * | |
| EEG-CNN [56] | 44.0 | 51.5 | 55.2 | 59.6 | 17 * | 26 * | |
| MI-SCNN [57] | 44.0 | 47.0 | 51.1 | 53.8 | 20.5 | 22.4 * | |
| MI-HFDNN [58] | 55.3 | 59.7 | 63.4 | 66.4 | - | - | |
| CFE-FSL MI [18] | 44.8 | 56.3 | 64.4 | 68.4 | - | - | |
| Multi-BioSig-Net (proposed) | 69.5 | 63.7 | 74.8 | 75.9 | 27.8 * | 34.2 * | |
| ER | SVM [25] | 58.1 | 60.2 * | 63.7 * | 64.5 * | 26.3 * | 31 * |
| EEGNet [26] | 61.0 | 62.2 * | 64.5 * | 66.7 * | 11.8 * | 21.7 * | |
| TPT [27] | 60.5 | - | - | - | - | - | |
| TCA [28] | 55.0 | - | - | - | - | - | |
| KPCA [29] | 56.8 | - | - | - | - | - | |
| MAML + ResNet-18 [24] | 70.0 | - | - | - | - | - | |
| Multi-BioSig-Net (proposed) | 66.7 | 69.4 | 73.7 | 75.1 | 27.8 * | 34.2 * | |
| SS | MetaSleepLearner [30] | 64.1 * | 67.2 * | 72.1 | 74.8 * | 5.2 * | 17.3 * |
| SleepEEGNet [31] | 71.5 * | 76.6 * | 84.3 | 84.5 * | 2.6 | 11.7 * | |
| DeepSleepNet [32] | 70.2 * | 75.9 * | 82.0 | 85.6 * | 24.7 | 34 * | |
| DeepSleepNet-Lite [33] | 72.4 * | 77.3 * | 84.0 | 85.1 * | 0.6 | 10.4 * | |
| AttnSleep [34] | 75.6 * | 79.2 * | 84.4 | 86.8 * | 31.8 * | 45.2 * | |
| XSleepNet [35] | 78.1 * | 80.6 * | 86.0 | 88.5 * | 5.6 | 16.7 * | |
| Average Ensemble [36] | - | - | 85.4 | - | 0.2 * | 11.8 * | |
| SleepFCN [38] | - | - | 84.8 | - | - | - | |
| ResNetMHA [39] | - | - | 84.3 | - | - | - | |
| IITNet [40] | - | - | 83.9 | - | - | - | |
| TPON [41] | - | - | 87.1 | - | - | - | |
| Multi-BioSig-Net (proposed) | 81.6 | 83.4 | 87.3 | 88.2 | 27.8 * | 34.2 * |
| Model | Task | 1-Shot | 5-Shot | 10-Shot | 20-Shot | P | IT |
|---|---|---|---|---|---|---|---|
| Meta-L MI [15] | MI | 53.2 | 61.4 | 65.7 | 68.6 | 97.4 * | 42.7 * |
| ER | 48.6 | 54.2 | 58.1 | 60.0 | |||
| SS | 45.1 | 51.6 | 52.9 | 55.7 | |||
| FSL-DA MI [16] | MI | 61.7 | 68.3 | 71.6 | 73.5 | 196.6 * | 63 * |
| ER | 55.3 | 58.7 | 60.1 | 63.8 | |||
| SS | 51.5 | 53.7 | 57.1 | 59.4 | |||
| MI RelationNet [1] | MI | 52.0 | 56.3 | 59.8 | 61.6 | 86.3 * | 42.7 * |
| ER | 49.6 | 51.5 | 53.1 | 55.7 | |||
| SS | 47.4 | 51.3 | 52.6 | 54.8 | |||
| EEG-CNN [56] | MI | 48.4 | 56.3 | 60.5 | 65.7 | 17 * | 26 * |
| ER | 48.2 | 55.9 | 60.3 | 65.2 | |||
| SS | 47.8 | 55.4 | 59.7 | 64.8 | |||
| MI-SCNN [57] | MI | 43.3 | 44.6 | 46.5 | 49.6 | 20.5 | 22.4 * |
| ER | 40.7 | 42.4 | 43.6 | 45.1 | |||
| SS | 40.2 | 41.6 | 43.0 | 44.6 | |||
| SVM [25] | MI | 55.7 | 59.4 | 61.3 | 62.3 | 26.3 * | 31 * |
| ER | 58.1 | 61.4 | 63.6 | 64.5 | |||
| SS | 53.6 | 56.7 | 58.6 | 59.6 | |||
| EEGNet [26] | MI | 58.7 | 61.2 | 65.5 | 68.8 | 11.8 * | 21.7 * |
| ER | 60.0 | 63.5 | 67.8 | 72.6 | |||
| SS | 56.8 | 60.3 | 62.6 | 65.3 | |||
| MetaSleepLearner [30] | MI | 57.3 | 61.6 | 64.8 | 68.1 | 5.2 * | 17.3 * |
| ER | 58.4 | 62.9 | 64.3 | 67.3 | |||
| SS | 61.6 | 67.4 | 70.6 | 73.2 | |||
| SleepEEGNet [31] | MI | 69.4 | 71.6 | 74.3 | 76.7 | 2.6 | 11.7 * |
| ER | 66.7 | 68.1 | 70.2 | 73.8 | |||
| SS | 73.7 | 78.4 | 81.6 | 82.5 | |||
| DeepSleepNet [32] | MI | 66.2 | 70.1 | 73.4 | 75.7 | 24.7 | 34 * |
| ER | 64.6 | 67.2 | 69.3 | 72.9 | |||
| SS | 70.3 | 75.8 | 79.6 | 82.4 | |||
| DeepSleepNet-Lite [33] | MI | 68.5 | 72.8 | 74.6 | 76.1 | 0.6 | 10.4 * |
| ER | 67.3 | 70.1 | 73.5 | 75.2 | |||
| SS | 72.7 | 78.4 | 81.3 | 83.6 | |||
| AttnSleep [34] | MI | 71.0 | 74.3 | 77.1 | 79.8 | 31.8 * | 45.2 * |
| ER | 70.4 | 72.8 | 76.5 | 78.3 | |||
| SS | 73.6 | 79.1 | 82.4 | 84.2 | |||
| XSleepNet [35] | MI | 77.4 | 80.5 | 83.9 | 87.7 | 5.6 | 16.7 * |
| ER | 76.8 | 78.2 | 82.9 | 86.3 | |||
| SS | 79.5 | 83.6 | 88.6 | 89.2 | |||
| Average Ensemble [36] | MI | 65.3 | 67.9 | 71.2 | 74.2 | 0.2 * | 11.8 * |
| ER | 61.6 | 65.8 | 70.8 | 72.3 | |||
| SS | 70.5 | 76.7 | 81.7 | 83.6 | |||
| Multi-BioSig-Net (proposed) | MI | 78.5 | 82.7 | 84.5 | 87.9 | 27.8 * | 34.2 * |
| ER | 78.3 | 80.1 | 81.7 | 84.8 | |||
| SS | 80.4 | 85.6 | 89.3 | 91.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, N.; Kim, S.G.; Kim, J.S.; Jeong, M.S.; Park, K.R. A Blind Few-Shot Learning for Multimodal-Biological Signals with Fractal Dimension Estimation. Fractal Fract. 2025, 9, 585. https://doi.org/10.3390/fractalfract9090585
Ullah N, Kim SG, Kim JS, Jeong MS, Park KR. A Blind Few-Shot Learning for Multimodal-Biological Signals with Fractal Dimension Estimation. Fractal and Fractional. 2025; 9(9):585. https://doi.org/10.3390/fractalfract9090585
Chicago/Turabian StyleUllah, Nadeem, Seung Gu Kim, Jung Soo Kim, Min Su Jeong, and Kang Ryoung Park. 2025. "A Blind Few-Shot Learning for Multimodal-Biological Signals with Fractal Dimension Estimation" Fractal and Fractional 9, no. 9: 585. https://doi.org/10.3390/fractalfract9090585
APA StyleUllah, N., Kim, S. G., Kim, J. S., Jeong, M. S., & Park, K. R. (2025). A Blind Few-Shot Learning for Multimodal-Biological Signals with Fractal Dimension Estimation. Fractal and Fractional, 9(9), 585. https://doi.org/10.3390/fractalfract9090585






