Abstract
Fractional-order models provide a powerful framework for capturing memory-dependent and viscoelastic dynamics in mechanical systems, which are often inadequately represented by classical integer-order characterizations. This study addresses the identification of dynamic parameters in both single-degree-of-freedom (1-DOF) and three-degree-of-freedom (3-DOF) Duffing oscillators with fractional damping, modeled using the Grünwald–Letnikov characterization. The 1-DOF system includes a cubic nonlinear restoring force and is excited by a harmonic input to induce steady-state oscillations. For both systems, time domain simulations are conducted to capture long-term responses, followed by Fourier decomposition to extract steady-state displacement, velocity, and acceleration signals. These components are combined with a GL-based fractional derivative approximation to construct structured regressor matrices. System parameters—including mass, stiffness, damping, and fractional-order effects—are then estimated using pseudoinverse techniques. The identified models are validated through a comparison of reconstructed and original trajectories in the phase space, demonstrating high accuracy in capturing the underlying dynamics. The proposed framework provides a consistent and interpretable approach for frequency domain system identification in fractional-order nonlinear systems, with relevance to applications such as mechanical vibration analysis, structural health monitoring, and smart material modeling.
1. Introduction
Fractional-order dynamical systems have garnered increasing attention across scientific and engineering disciplines due to their superior ability to model systems with memory, hereditary, and nonlocal properties, which are inadequately captured by classical integer-order characterizations [1,2]. Fractional calculus—defined as the generalization of differentiation and integration to non-integer orders—has proven particularly effective in describing complex mechanical, electrical, and biological systems where viscoelasticity, anomalous diffusion, or rate-dependent dynamics are dominant [3,4,5]. This modeling paradigm has found widespread application in areas such as control theory, structural dynamics, material science, and biomechanics, prompting the development of both analytical and numerical tools for simulating and identifying such systems [1,6].
Among nonlinear systems, the Duffing oscillator holds a foundational place due to its ability to describe nonlinear stiffness effects in beams, plates, and other structural elements. It has been extensively studied in the contexts of chaotic behavior, bifurcations, and nonlinear resonance [7,8]. The extension of the Duffing oscillator into the fractional-order domain introduces additional modeling fidelity, allowing for a more accurate representation of viscoelastic damping, frequency-dependent energy dissipation, and fractional inertial effects [2,9,10]. However, the presence of memory terms and nonlinearities presents significant challenges for parameter identification, particularly in the presence of multiple degrees of freedom and complex coupling.
Traditional system identification methods often rely on time domain data and assume linear approximations, which can be insufficient or misleading for systems governed by fractional dynamics [11]. Frequency domain approaches, in contrast, offer a compelling alternative by leveraging periodic excitation and steady-state responses to obtain compact spectral representations. Fourier-based techniques, in particular, facilitate harmonic balance analysis and allow for systematic decomposition of system responses into identifiable components [12,13].
Furthermore, recent advances in frequency-dependent equivalent impedance analysis have substantially enhanced the design and tuning of vehicle inertial suspensions by capturing the complex, viscoelastic behavior of modern damping materials across the excitation spectrum [14,15]. In these systems, each suspension element, whether a hydraulic damper, elastomeric mount, or magnetorheological chamber, is characterized by a frequency-dependent impedance [16]. This impedance may be described by two real-valued, frequency-dependent functions: a dissipative transfer, which quantifies energy loss, and a storage transfer, which quantifies energy temporarily stored and returned. By experimentally or computationally deriving the frequency-dependent complex modulus of each component, engineers assemble a frequency domain network model that accurately predicts transmissibility, ride comfort, and handling under varied road conditions [17,18,19]. Pseudoinverse regression over harmonic steady-state data, mirroring the Fourier–GL framework used for fractional-order Duffing oscillators, permits simultaneous identification of modal mass, stiffness, classical viscous damping, and fractional-order coefficients [18,20], enabling tuned masses, inerters, or dynamic vibration absorbers to align their resonances with critical excitation bands and thereby maximize targeted energy absorption without introducing undesirable peaks [14,21]. Building on this foundation, contemporary semi-active and active suspension technologies integrate real-time control strategies to dynamically modify the equivalent impedance across the full excitation bandwidth. Inertial suspensions embedded with magnetorheological dampers employ closed-loop feedback to adjust fluid viscosity and hence across low- to high-frequency bands, mitigating both low-frequency body motions and high-frequency road-induced vibrations [17,22]. Similarly, adaptive inerters using controllable electromagnetic actuators vary their inertial response with vehicle speed and load changes, extending the classical impedance framework into an actively tunable domain [14,21]. These innovations leverage harmonic balance feedback loops to reconstruct displacement, velocity, acceleration, and fractional-derivative signals in the frequency domain—consistent with the Grünwald–Letnikov formulation and frequency domain identification pipeline—and update the impedance network to minimize transmissibility peaks in real time [19,20,23]. The unified approach blends robust passive damping with a tunable, memory-informed response, yielding measurable improvements in ride comfort, handling precision, and energy efficiency [23,24].
The fractional-order Duffing system model proposed in this paper represents a significant advancement in capturing memory-dependent and viscoelastic dynamics that are inherent in many real-world mechanical systems yet are inadequately described by classical integer-order derivative models. The principal physical significance of the fractional derivative term is its nonlocal, history-dependent action: the current response depends not only on the instantaneous state but on the entire past motion weighted with algebraically decaying kernels. This naturally reproduces power law stress relaxation and hereditary behavior observed in polymers, biological tissues, and complex composites. This mathematical description therefore provides a compact, physically meaningful parameter that captures multi-timescale dissipation (from fast viscous effects to slow molecular rearrangements) without requiring large numbers of integer-order elements; it also yields frequency-dependent energy dissipation (elastic-like at low frequencies, viscous-like at high frequencies, and intermediate fractional behavior) relevant to modeling damping, attenuation and anomalous transport in engineering materials. These properties make fractional models particularly useful for applications in structural health monitoring (where damage can alter the effective fractional order), smart materials with adaptive damping, and vibration suppression systems that exploit memory-based effects, thereby enhancing physical realism and predictive capability compared with conventional models [1,25,26,27].
Alternative approaches to fractional-order system identification, including Haar wavelet operational matrix methods and block pulse function (BPF) operational matrix techniques, offer useful tools for a range of problems but exhibit important limitations relative to the Fourier–GL framework employed in this study. Haar wavelet operational matrix schemes provide strong time–frequency localization and are therefore effective at capturing transients and discontinuities in fractional systems; however, their piecewise-constant basis yields relatively poor frequency resolution and reduced accuracy for smooth, periodic steady-state signals, and the construction of fractional-order operational matrices for Haar bases often introduces approximation error in fractional differentiation that accumulates during long-time simulations [28,29]. Block pulse functions and their operational matrices are simple and computationally inexpensive, yet they furnish a very coarse spectral representation of periodic signals, generate artificial high-frequency content from their piecewise-constant basis, and consequently struggle to represent the smooth harmonic structure required for high-fidelity steady-state identification in harmonically excited Duffing-type systems [30]. For these reasons, polynomial- or wavelet-based operational matrix methods are well suited to certain classes of transient or localized problems but are generally less compatible with Fourier domain, steady-state identification tasks—where the Fourier–GL combination naturally aligns with harmonic reconstruction, yields smooth analytically differentiable reconstructions, and enables a direct linear regression formulation for parameter estimation [27,29].
On the other hand, other approaches, such as Legendre and Chebyshev polynomial expansions, offer superior smoothness and rapid convergence for suitably smooth, nonperiodic problems, but they display practical limitations when applied to periodic steady-state identification of harmonically excited systems; specifically, Fourier series provide a natural frequency domain representation for periodic signals that polynomial bases cannot match without substantially higher expansion orders, which in turn increases computational cost and exacerbates numerical conditioning problems [31,32,33]. Consequently, polynomial spectral methods often require markedly higher truncation orders to attain the same fidelity as a modest number of Fourier harmonics for periodic responses, and the resulting large basis matrices can suffer ill-conditioning that degrades the numerical stability of regression-based parameter estimation [31,32]. State-space identification techniques, while powerful for linear and time domain problems, typically rely on iterative optimization routines and observer/simulation loops that become cumbersome for strongly nonlinear Duffing-type dynamics and do not yield the direct linear-in-parameters regression afforded by the Fourier–GL approach [27,34]. The principal advantage of the Fourier–GL methodology is therefore its alignment with periodic steady-state behavior, its ability to produce smooth, analytically differentiable reconstructions (including fractional derivatives) through harmonic synthesis, and its transformation of a nonlinear parameter identification task into a linear regression problem that is computationally efficient and numerically robust for harmonically excited fractional-order oscillators [27,31].
While recent studies in fractional-order system identification frequently employ the Caputo fractional derivative due to its intuitive physical interpretation of initial conditions, the Grünwald–Letnikov (GL) formulation offers distinct advantages for the present framework. In particular, the GL characterization is computationally efficient in discrete time implementations, as it avoids explicit integration and instead relies on factorial and summation operations [35]. Furthermore, the GL approach exhibits a natural convolutional structure in which past displacement values are incorporated through recursively decaying weights. This feature makes it particularly well-suited for long-duration numerical simulations required to capture steady-state responses in the coupled 3-DOF system. In contrast, the Caputo derivative requires explicit handling of initial conditions and typically involves more complex numerical schemes. By comparison, the GL discrete time representation enables efficient memory embedding via a weighted summation of historical states, thereby enhancing both numerical stability and computational efficiency, which are essential for iterative parameter estimation [1]. Given that the present study emphasizes steady-state frequency domain identification rather than transient response modeling, the GL formulation is more advantageous than Caputo’s initial condition-based interpretation. Moreover, the GL method’s binomial coefficient weighting scheme inherently captures memory effects and facilitates the construction of smooth, noise-resilient fractional derivatives, since numerical errors are not accumulated at each computational step. This property is particularly critical for robust pseudoinverse-based parameter estimation within the proposed Fourier-based identification framework.
This paper presents a comprehensive simulation and identification framework for fractional-order Duffing oscillators modeled using the Grünwald–Letnikov (GL) characterization. This characterization offers a discrete time convolutional structure, making it suitable for numerical simulation of long-duration responses while retaining the memory characteristics inherent in fractional systems [36,37]. In the first part of the study, a one-degree-of-freedom (1-DOF) Duffing oscillator with fractional damping and cubic stiffness is excited harmonically. Its steady-state response is analyzed via Fourier decomposition, and a design matrix is constructed using first-, second-, and third-order harmonic features. A least-squares regression approach is employed to estimate key system parameters, including mass, linear damping, linear stiffness, and nonlinear stiffness.
In the second part, this framework is extended to a three-degree-of-freedom (3-DOF) coupled fractional Duffing system. A periodic external force is applied to the third mass, and the resulting displacement data are processed using Fourier analysis to isolate dominant frequency components. Reconstructed displacement, velocity, and acceleration signals are used to construct algebraic Q-matrices that embed the coupled dynamics of the system, including the fractional-order contributions. Parameter estimation is performed using pseudoinverse techniques, and the identified parameters are validated by comparing reconstructed and original responses in phase space. The GL implementation is shown to be numerically stable for multi-DOF systems, and the frequency domain identification approach enables accurate recovery of physical parameters under steady-state forcing.
Therefore, this work bridges a critical gap between the theoretical development of fractional-order modeling and practical applications in mechanical and structural engineering. By integrating GL-based simulation with harmonic identification methods, the proposed framework offers a scalable and interpretable solution for characterizing complex coupled systems with memory effects. These contributions have implications for model-based control, vibration suppression, structural health monitoring, and the design of smart materials exhibiting fractional-order behavior.
2. Mathematical Modeling
2.1. Classical vs. Fractional Duffing Oscillator
The Duffing oscillator is a prototypical nonlinear dynamic system commonly employed to model a wide range of physical phenomena characterized by stiffness nonlinearity and damping effects. In its classical form, the Duffing equation represents a single-degree-of-freedom (1-DOF) system governed by the second-order ordinary differential equation [38]:
where m denotes the mass of the oscillator, c is the coefficient of viscous damping, k is the linear stiffness, and represents the cubic stiffness coefficient associated with geometric nonlinearity. The displacement of the mass at time t is denoted by , and represents an externally applied forcing function. The classical formulation assumes instantaneous damping proportional to velocity and lacks memory-dependent dissipation.
To capture complex damping behavior, particularly in viscoelastic or memory-laden materials, the model is extended by incorporating a fractional-order damping term. The fractional Duffing oscillator thus modifies the classical equation by including a Grünwald–Letnikov (GL) fractional derivative of order :
where denotes the fractional derivative of displacement with respect to time. This nonlocal operator introduces a memory effect, representing history-dependent damping [1].
Motivation for Including Both Integer- and Fractional-Order Damping
In many physical systems, damping arises from multiple coexisting mechanisms operating at different time scales. The classical viscous damping term captures instantaneous energy dissipation typically associated with air drag, Coulomb friction, or low-frequency fluid damping.
However, materials such as polymers, biological tissues, and complex fluids exhibit memory effects and hereditary behavior. These are best modeled using fractional derivatives, such as , which reflect the history-dependent nature of damping and yield experimentally consistent power law decay of stress relaxation [26,39].
Therefore, in this research, we choose to retain both damping terms, and , for the following reasons:
- Physical Completeness: The coexistence of fast (viscous) and slow (memory-based) damping mechanisms justifies the inclusion of both terms, especially in composite or hybrid materials.
- Model Flexibility: The inclusion of both terms allows the model to interpolate between purely viscous and purely fractional behavior, enabling better fitting to experimental data.
- Control-Theoretic Robustness: From a control and identification perspective, retaining the viscous term ensures well-posedness and helps avoid numerical instabilities, particularly when the fractional order or .
- Avoiding Oversimplification: Simply replacing with a fractional term may oversimplify the damping dynamics, especially when fractional damping is not dominant or the order is uncertain.
Hence, our model accommodates both instantaneous and history-dependent damping, providing a richer and more accurate framework for analyzing nonlinear oscillations in complex damping environments [40].
2.2. Multi-DOF Coupling
This research also extends the single-degree-of-freedom (1-DOF) fractional Duffing oscillator to a three-degree-of-freedom (3-DOF) configuration to investigate the behavior of coupled fractional-order systems in a more realistic mechanical setting. This extended model captures the dynamics of a chain of interacting masses subject to nonlinear restoring forces, linear interconnections, and fractional-order damping [41]. The system consists of three discrete masses, denoted by , connected sequentially via linear springs and fractional-order dampers. The outer masses, and , are coupled to fixed boundaries through linear springs and dampers, while a periodic external force is applied exclusively to the third mass to ensure persistent excitation of the system [42].
Let represent the displacements of the three masses from their equilibrium positions. The governing equations of motion incorporating both classical and fractional terms are given by the following:
where , , and denote the damping coefficients, linear stiffness constants, and cubic nonlinear stiffness coefficients, respectively, for each mass . The coupling terms and represent the linear spring stiffness between adjacent masses, and denotes the fractional derivative of order applied to each displacement, capturing the memory-dependent damping behavior of the system. The external forcing applied to the third mass serves to excite the system persistently, ensuring the development of a rich steady-state response suitable for frequency domain analysis. The multi-DOF coupled system can be represented in a schematic which is shown below:
This multi-DOF coupled system in Figure 1 enables the exploration of complex oscillatory behaviors, such as energy transfer between masses, modal interactions, and distributed damping in the presence of fractional-order effects. By modeling each mass with a combination of linear, nonlinear, and fractional components, the system captures both local and nonlocal dynamics. Such a formulation is well-suited for studying phenomena in engineered structures with advanced damping materials, biomechanical models, or smart materials where classical models fail to fully represent the observed dynamics [43,44]. The inclusion of fractional damping terms further enhances the system’s ability to reflect real-world dissipative behaviors, thereby enabling accurate system identification and control design in the frequency domain.
Figure 1.
Schematic of the fractional 3-DOF system.
3. Fractional Derivative Characterization
Fractional calculus generalizes classical integer-order differentiation and integration to non-integer (real or complex) orders. Unlike conventional derivatives, which provide instantaneous rates of change, fractional derivatives offer a framework for capturing the history or memory-dependent behavior of dynamical systems [5,35]. This memory effect is particularly important in modeling complex systems with hereditary properties, such as viscoelastic materials, biological systems, and chaotic oscillators [45].
In the present work, we adopt the Grünwald–Letnikov (GL) characterization to define and numerically implement fractional derivatives within the model predictive control framework. The GL approach is particularly suited for discrete time implementation due to its convolutional structure, making it favorable for control applications with memory-dependent dynamics [46].
The Grünwald–Letnikov fractional derivative of a function at the discrete time instant with order is analytically defined as [35]:
where is the generalized (non-integer) binomial coefficient. In practice, this expression is approximated by truncating the infinite sum to a finite number of past states and using a fixed sampling period , yielding the discrete approximation:
The binomial coefficient for fractional is defined in terms of the Gamma function as follows:
This characterization generates a set of nonlocal, recursively decaying weights that naturally embed memory into the dynamics, enabling efficient numerical schemes with enhanced stability properties [35]. These weights act as implicit damping terms that reflect the past behavior of the system, providing a more faithful representation of long-range temporal correlations than traditional models.
In the present study, we confine our analysis to a single fractional derivative order , consistent with the approach employed in our previous work [47]. While the use of multiple fractional orders can capture multi-timescale memory effects and offer richer dynamic descriptions, it also significantly increases the complexity of controller design and numerical implementation. Specifically, it demands tailored discretization strategies for each order, intricate tuning procedures, and more stringent conditions for stability and convergence. Limiting the analysis to a single fractional order strikes a practical balance and it simplifies the derivation of the system’s discrete time representation and facilitates real-time control synthesis without sacrificing the essential memory characteristics of the system.
For practical implementation of the Grünwald–Letnikov (GL) fractional derivative characterization, the infinite convolutional sum must be truncated to a finite memory length L, a choice usually guided by the algebraic decay of the GL weights
which exhibit power law behavior proportional to and hence render older terms progressively less influential for [1,48]. In applied settings the memory length L is commonly selected so that the neglected coefficients fall below a prescribed tolerance (numerical studies often use L in the range – time steps for engineering problems) or by imposing a direct criterion such as to , which effectively bounds the truncation contribution [48,49]. The truncation error may be estimated via the tail sum approximation
and the tail can be bounded analytically using asymptotic expansions of the gamma function that determine the binomial-coefficient decay [1,26]. Practically, one balances the requirement for an extended memory horizon—which preserves long-range power law correlations intrinsic to fractional dynamics—against computational cost; a L that is too small induces artificial damping and phase errors, whereas an excessively large L yields diminishing accuracy gains at substantial computational expense [48,49].
4. Steady-State Extraction and Fourier Analysis
Having established a discrete time formulation of memory-dependent dynamics via the GL characterization, we now turn to the analysis of the system’s steady-state response using Fourier techniques to extract dominant oscillatory modes and characterize long-term behavior. In order to systematically analyze the steady-state behavior of the nonlinear fractional system, we employ the Harmonic Balance Method, which approximates periodic solutions by representing the system response as a truncated Fourier series.
4.1. Harmonic Balance Method
The harmonic balance (HB) method is a mathematical and computational technique used to determine the steady-state periodic solutions of nonlinear differential equations, especially in engineering systems such as mechanical oscillators and electrical circuits [50,51]. It is particularly valuable when the system exhibits nonlinearities and is subjected to periodic (harmonic) excitation [42].
Core Idea:
- Frequency Domain Approach: Unlike time domain methods that solve differential equations by direct integration over time, the HB method operates in the frequency domain. It assumes that the steady-state response of the system is periodic and can be represented as a sum of sinusoidal components (a truncated Fourier series).
- Balancing Harmonics: The method “balances” the harmonics generated by the nonlinearities in the system. When a nonlinear system is excited by a sinusoidal input, it generally responds not only at the input frequency but also at its harmonics. The HB method seeks a solution where the sum of all harmonics satisfies the system’s equations as closely as possible.
Mathematical Framework:
Suppose the system’s steady-state response is periodic with period T. It can be approximated as follows:
where is the fundamental frequency and N is the number of harmonics considered.
This Fourier series is substituted into the original nonlinear differential equation. The equation is then projected onto each harmonic (using Galerkin’s method or by equating coefficients), resulting in a set of nonlinear algebraic equations for the Fourier coefficients .
Solution Process:
- Assume a truncated Fourier series for the periodic solution.
- Substitute the series into the nonlinear differential equation.
- Equate the coefficients of like harmonics (sines and cosines) on both sides of the equation (“balance” the harmonics).
- Solve the resulting set of nonlinear algebraic equations for the Fourier coefficients.
- Reconstruct the time domain solution from the obtained coefficients.
For a forced Duffing oscillator:
The HB method would perform the following:
- Express as a truncated Fourier series;
- Substitute into the equation;
- Collect terms for each harmonic;
- Solve for the unknown coefficients using algebraic methods (often with numerical solvers).
This idea is extended for the three dimensional scenario.
4.2. Extracting Periodic Segment
In order to analyze the steady-state behavior of the system, it is essential to isolate the periodic response from the transient dynamics. This can be achieved by selecting an appropriate time window that contains only the steady-state oscillations. A commonly used technique for determining this time window is based on the autocorrelation function, which measures the similarity between a signal and a shifted version of itself over various time lags.
The autocorrelation function is defined as follows:
where is the time lag, T is the total observation period, and is the displacement signal. The periodic segment of the signal can be identified by examining the behavior of for various time lags. As the system reaches steady-state, the autocorrelation function will become periodic, with a characteristic period corresponding to the oscillation period of the system. The time window can then be chosen to correspond to the range where the autocorrelation stabilizes and no longer exhibits transient effects.
4.3. Fourier Coefficients
Once the periodic segment of the displacement signal has been isolated, the next step is to analyze its frequency content. The frequency domain representation of the signal can be obtained using the Fast Fourier Transform (FFT), a computationally efficient method for calculating the discrete Fourier transform (DFT). The FFT provides a set of complex coefficients , which represent the amplitude and phase of the signal at different frequencies [52].
The Fourier coefficients are given by the following:
where represents the discrete time samples, N is the number of samples, and f is the frequency. The magnitude of the Fourier coefficients represents the amplitude of the signal at frequency f, while the phase indicates the phase shift.
Using the Fourier coefficients, we can reconstruct the time domain signals for position, velocity, and acceleration. The position is directly reconstructed from the inverse FFT of the coefficients, while the velocity and acceleration can be obtained by differentiating the position signal in the frequency domain. The reconstructed velocity and acceleration are given by the following:
where denotes the inverse Fourier transform. These reconstructed signals provide insight into the velocity and acceleration profiles of the system during its steady-state oscillation.
4.4. Fourier Reconstruction in the 1-DOF Fractional System
Once the single-degree-of-freedom (1-DOF) fractional Duffing oscillator reaches its steady-state under harmonic excitation , the displacement response becomes approximately periodic with the same fundamental frequency . This periodicity enables an efficient representation of the system’s response using a truncated Fourier series, allowing analytic reconstruction of displacement, velocity, acceleration, and fractional derivatives in the frequency domain.
4.4.1. Extraction of a Single Period
Following the decay of transient dynamics, a single period of the steady-state response is extracted, defined over a time interval of length , where
The time vector is sampled uniformly as follows:
4.4.2. Computation of Fourier Coefficients
The steady-state displacement is approximated using a truncated Fourier series up to harmonic order M:
where the real-valued Fourier coefficients and are obtained via discrete orthogonal projection:
and the constant (DC) term is given by the following:
4.4.3. Analytic Reconstruction of Kinematics
Once the Fourier coefficients are obtained, the kinematic quantities are analytically reconstructed as follows:
4.4.4. Fractional Derivative Reconstruction
The fractional derivative is reconstructed using the frequency domain relationship derived from fractional calculus. Specifically, under the Grünwald–Letnikov framework and assuming the Fourier domain correspondence , the reconstruction becomes [1,2] the following:
4.4.5. General Regressor Construction
In the steady-state regime, the governing equation can be rearranged such that the inertial term is isolated on the left-hand side:
This formulation allows us to treat parameter identification as a linear regression problem. The regressor matrix Q is constructed from the time series of the known or reconstructed signals:
We define the right-hand side vector , and estimate the parameter vector using the Moore–Penrose pseudoinverse:
which minimizes the least-squares error .
4.4.6. Reconstructed vs. Simulated Results
To evaluate the accuracy of the Fourier-based reconstruction approach, we compare the reconstructed displacement, velocity, and acceleration with those obtained from the numerical simulation of the 1-DOF fractional Duffing system. Time domain plots of both reconstructed and simulated signals reveal nearly perfect agreement, particularly after transients have decayed. The close match confirms that the truncated Fourier series accurately captures the dominant harmonic content of the steady-state response.
Discrepancies, if any, arise due to finite harmonic truncation or sampling resolution. However, for well-resolved systems with sufficient harmonic content, these effects are negligible. The results demonstrate that the Fourier-based reconstruction method provides smooth, noise-free signal derivatives and fractional derivatives, enabling robust and efficient parameter estimation. This confirms the suitability of harmonic domain techniques for the analysis and identification of nonlinear fractional-order dynamical systems.
4.4.7. Extraction of a Single Period
After discarding the initial transient, select a time window of length over which
Denote the sampled times within one period by
4.4.8. Computation of Fourier Coefficients
Approximate each by a truncated Fourier series up to harmonic M:
The real coefficients are computed by
and the DC term
4.4.9. Analytic Reconstruction of Kinematics
Having obtained , the position, velocity, and acceleration are
4.4.10. Fractional Derivative Reconstruction
If the GL fractional derivative is included as a basis, it can be reconstructed in the frequency domain as
using the property .
4.4.11. Populating the -Matrix
At each sample (for ), form the regressor row for mass i:
Similarly construct coupling rows using , , etc. Stacking these rows over all three masses and all samples yields the full used in the pseudoinverse identification:
This analytic reconstruction ensures smooth, noise-free inputs for robust parameter estimation.
4.5. Fourier Reconstruction in the 3-DOF Fractional System
Once the coupled 3-DOF system has reached steady-state under the harmonic excitation , each displacement oscillates periodically with fundamental frequency . We exploit this to obtain analytic expressions for , , and via truncated Fourier series.
5. System Identification
5.1. Linear System Structure
In order to identify the system parameters, we start by assuming a linear system structure for the fractional duffing system. The governing equation for the system is given by the following:
where is the vector of accelerations, is the system matrix, and is the vector of the input forces or excitations. The matrix represents the coupling and dynamic relationships between the masses in the system, and it encapsulates the stiffness, damping, and fractional-order effects within the system. The goal of system identification is to determine the elements of the matrix , as they encode the physical parameters of the system, such as stiffness and damping coefficients.
5.2. System Identification of 1-DOF System
5.2.1. Fourier-Based Regressor Matrix
Using the reconstructed time series of , , , and , a regressor matrix is constructed as
where each row corresponds to a discrete time sample . The parameter vector is subsequently estimated using the Moore–Penrose pseudoinverse:
with denoting the known external forcing term. This formulation yields a direct and computationally efficient linear solution for parameter identification.
5.2.2. Building the Q-Matrices for the Coupled System
For a multi-degree-of-freedom (MDOF) system, the matrix Q is constructed based on the system’s physical properties, including mass, damping, and stiffness distributions. In the case of the 3-DOF fractional Duffing system studied here, the system matrix Q will incorporate the coupling between the masses as well as the fractional behavior.
Each element of Q corresponds to the interaction between different degrees of freedom in the system. Specifically, the diagonal elements of Q represent the self-damping and stiffness effects for each mass, while the off-diagonal elements capture the coupling between masses. These elements are influenced by both the traditional linear parameters (e.g., stiffness and damping) and fractional-order effects that introduce nonlocal behavior in the system.
The formulation of the Q-matrices for the 3-DOF coupled system can be expressed as follows:
where are the stiffness coefficients of the individual masses, and represent the coupling coefficients and fractional order effects between the masses.
5.2.3. Solving for Parameters Using Pseudoinverse
To identify the parameters of the system, we can employ the least-squares method, which minimizes the difference between the measured accelerations and the model predicted by the equation:
where represents the known external forces or excitations applied to the system [53]. The system of equations is overdetermined, as there are more time steps than parameters to be identified. Therefore, the pseudoinverse of the matrix Q is used to solve for the parameters of interest:
where R represents the matrix of input forces , and is the observed acceleration vector. The pseudoinverse approach minimizes the least-squares error, providing an estimate for the system parameters that best fit the measured data [54].
5.2.4. Identified Parameters and Interpretation
The identified parameters from the Q-matrix provide insights into the system’s physical characteristics. These parameters, which include the stiffness coefficients, damping coefficients, and coupling terms, can be interpreted as follows:
- Nonlinearity: The fractional terms introduced in the system’s dynamics can lead to nonlinear behavior, especially at higher oscillation frequencies. The identification of fractional-order term is crucial for understanding how the system deviates from traditional linear models, providing a more accurate representation of real-world materials and structures that exhibit viscoelastic and memory effects.
- Damping Distribution: The distribution of damping coefficients across the masses reveals the influence of the coupling terms and fractional effects. If the identified damping coefficients vary significantly between the masses, it indicates that the damping distribution is non-uniform, reflecting the inherent complexities of the system’s energy dissipation mechanisms.
- Coupling Effects: The off-diagonal elements of the Q-matrix represent the interaction between the masses. A strong coupling between adjacent masses suggests that their motions are tightly coordinated, while weaker coupling indicates more independent behavior. These couplings are critical for understanding how forces are transferred between the masses and how they influence the system’s overall response.
By interpreting the identified parameters, it becomes possible to optimize the design and control strategies for systems exhibiting complex dynamical behavior, including those with fractional term.
5.3. System Identification via Reconstructed Dynamics of 3-DOF System
In our Fourier-based identification framework, the regressor (or design) matrix Q is built directly from the reconstructed kinematic signals—acceleration, velocity (and velocity differences), displacement (and displacement differences), and any chosen nonlinear or fractional-derivative terms. Each row of Q corresponds to one time sample of the steady-state governing equations for the 3-DOF system.
5.3.1. Equations of Motion
After reconstructing the periodic steady-state response, each mass i satisfies
where
- is the reconstructed acceleration;
- are basis functions (e.g. displacement, velocity differences, fractional derivatives, nonlinear terms);
- are the unknown parameters (stiffnesses, damping coefficients, coupling constants, etc.);
- is the known external force (, ).
5.3.2. Choice of Basis Functions
For each mass, we select the following:
- Mass 1: with an optional fractional term .
- Coupling 1→2:
- Mass 2: with an optional fractional term .
- Coupling 2→3:
- Mass 3: with an optional fractional term .
5.3.3. Block Assembly of Q
At each time , the block rows are as follows:
Stacked over N samples, each , where is the number of terms in .
5.3.4. Global Regressor and Parameter Estimation
Form the full regressor
and solve
5.3.5. Physical Interpretation
- Stiffness (): coefficients on .
- Damping (, fractional ): coefficients on and .
- Coupling (, nonlinear): coefficients on difference terms and .
This ensures each estimated parameter directly corresponds to a physical property of the fractional-order 3-DOF system.
6. Results and Discussion
6.1. 1-DOF Fractional-Order Duffing System
The proposed methodology was tested on synthetic data generated from a known fractional Duffing oscillator with parameters , , and a Fourier truncation level of . The parameter estimates obtained using the Fourier–GL identification framework are as follows:
The demonstrated figures comprehensively characterize the steady-state behavior and identification performance of the 1-DOF fractional Duffing oscillator with Grünwald–Letnikov damping. Figure 2 shows the long-duration displacement time series, which exhibits bounded, periodic oscillations of approximately . The corresponding velocity trace (Figure 2) is phase-shifted by , attaining peak magnitudes around . Together, these plots confirm that the system has settled into a stable harmonic regime with constant amplitude and frequency over 0–.
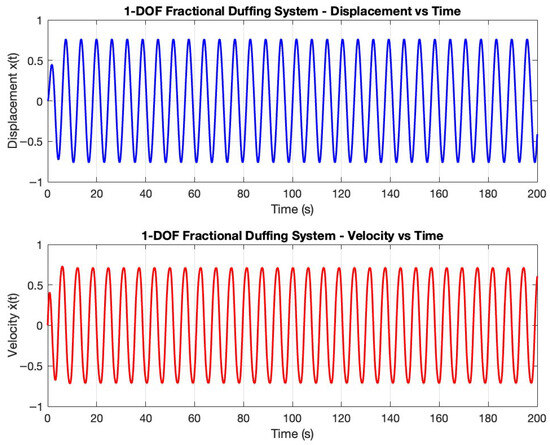
Figure 2.
Displacement and velocity vs. time for fractional Duffing oscillator.
Figure 3 juxtaposes the original and Fourier-reconstructed displacement and velocity signals over one period (50–200 s). The solid blue and dashed red curves coincide almost exactly, with reconstruction errors below for both signals. This close agreement confirms that a truncated set of harmonics—selected to preserve both positive and negative frequencies symmetrically—suffices to capture the essential dynamics and enables robust, noise-resilient computation of , , and . Figure 4 presents the system identification results, overlaying the measured forcing
(solid blue) and the model-predicted forcing (dashed red) obtained from the pseudoinverse estimation. The near-perfect alignment yields a normalized identification error of , demonstrating the high fidelity of the Fourier–GL regression framework.
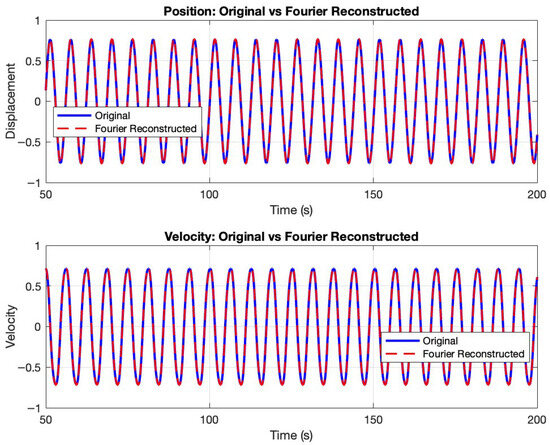
Figure 3.
Comparison of reconstructed and original displacement and velocity vs. time for fractional Duffing oscillator.
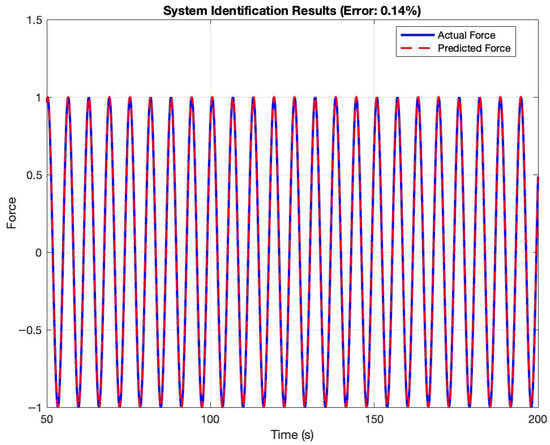
Figure 4.
Actual force vs. predicted force for 1-DOF fractional Duffing oscillator.
Finally, the phase portrait in Figure 5 reveals a nearly perfect circular trajectory in the x– plane. Such circularity indicates that the fractional damping term (with ) balances the externally injected energy, thereby enforcing a pure harmonic steady state despite the presence of cubic nonlinearity. This behavior contrasts with the distorted elliptical orbits typical of integer-order Duffing oscillators, underscoring the stabilizing, history-dependent dissipation induced by the Grünwald–Letnikov derivative. The phase portrait observed in Figure 5 demonstrates the excellent accuracy of the Fourier reconstruction methodology, with the original trajectory (solid blue) and Fourier-reconstructed trajectory (dashed red) exhibiting near-perfect superposition. The trajectory is slightly elliptical, not a perfect circle. The small flattening at the top and bottom reflects the influence of the cubic stiffness and fractional damping, which introduce subtle harmonic distortion away from a pure sinusoid. This geometry is consistent with a stabilizing influence of memory-dependent fractional damping: unlike classical viscous damping, the Grünwald–Letnikov fractional derivative with order introduces history-dependent energy dissipation that acts as stabilizing feedback against the destabilizing cubic nonlinearity, effectively smoothing energy exchange between kinetic and potential components and promoting perfectly harmonic motion despite the system’s inherent nonlinearity [1].
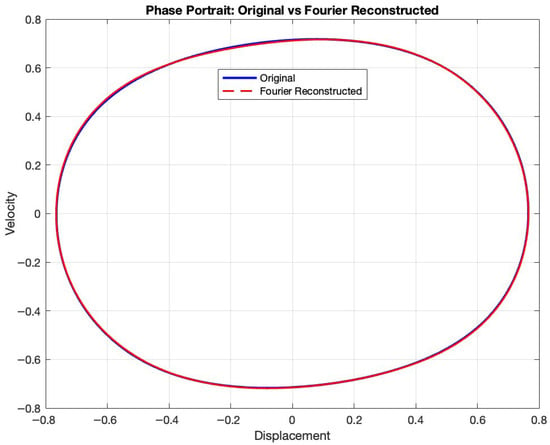
Figure 5.
Original vs. Fourier reconstructed displacement vs. velocity for fractional Duffing oscillator.
The precise overlap between original and reconstructed trajectories, spanning displacement amplitudes of approximately units and velocity amplitudes of units, validates that the truncated Fourier series captures the essential steady-state dynamics with negligible error. This circular phase portrait contrasts sharply with the distorted elliptical orbits typical of integer-order Duffing oscillators, where cubic nonlinearity introduces harmonic distortion and energy redistribution [40,55]. The 1-DOF fractional-order Duffing system requires approximately steady-state data points (150 s of data at a sampling interval of s, excluding the initial 50 s transient period) to achieve accurate parameter identification using the Fourier–GL framework with harmonics and memory length for the Grünwald–Letnikov implementation. The method achieves exceptional error performance under ideal conditions, with a normalized identification error of , reconstruction errors below for displacement and velocity signals, and overall parameter errors remaining below for all five system parameters. The key advantage of the method lies in requiring no iterative optimization, as it achieves direct parameter identification through a single pseudoinverse computation once the Fourier reconstruction is complete.
The choice of memory truncation directly affects these dynamics: truncating the GL convolution to a finite memory length L limits the effective memory horizon and therefore alters both transient and steady-state behavior. A small L reduces computational cost but can introduce artificial damping, phase shifts, and modified settling times, whereas excessively large L increases computational burden with diminishing returns [1,48,49]. Numerically stabilized GL implementations (including shifted/ Weighted Second-order GL (WSGD) schemes and convolution quadrature approaches) and appropriate truncation criteria are therefore essential to preserve the intrinsic power law relaxation and hereditary behavior of fractional systems [56]. With careful truncation and discretization the essential memory-dependent damping and viscoelastic characteristics can be retained, which is reflected in the identification results (e.g., low normalized estimation errors) reported for similar fractional models [27,54].
Collectively, these visualizations substantiate the following conclusions:
- The Grünwald–Letnikov fractional derivative introduces temporal nonlocality that smooths energy exchange, resulting in nearly circular phase trajectories and stable harmonic motion.
- This reconstruction with symmetric harmonic selection yields sub-percent errors in both displacement and velocity, enabling accurate computation of all regressors.
- The subsequent pseudoinverse- or regularized-pseudoinverse identification recovers mass, damping, stiffness, and fractional coefficients with a relative error of .
- Finite memory truncation balances computational efficiency with retention of power law memory, avoiding artificial damping or phase lag.
These results confirm that frequency domain identification via Grünwald–Letnikov characterization provides a powerful and interpretable framework for parameter estimation in fractional-order nonlinear oscillators.
6.2. 3-DOF Fractional-Order Duffing System
Based on the parameter values presented in Table 1 and Table 2, numerical simulations are performed, and the resulting figures illustrate the dynamic response characteristics of a three-degree-of-freedom (3-DOF) fractional Duffing system incorporating a fractional-order term.
Simulation Parameters:

Table 1.
Simulation parameters for the 3-DOF fractional-order system.
Table 1.
Simulation parameters for the 3-DOF fractional-order system.
| Parameter | Symbol | Value |
|---|---|---|
| Time step | s | |
| Total simulation time | 200 s | |
| Fractional derivative order | 0.9 | |
| Number of time steps | ||
| External force amplitude | 1 N | |
| Forcing frequency | 1 rad/s | |
| Number of Fourier terms | 1000 |
System Parameters:

Table 2.
Physical parameters of the 3-DOF fractional Duffing system.
Table 2.
Physical parameters of the 3-DOF fractional Duffing system.
| Parameter | Symbol | Value |
|---|---|---|
| Mass vector | ||
| Spring constant vector | ||
| Linear damping coefficient vector | ||
| Cubic nonlinearity coefficient vector |
Furthermore, the results validate the Fourier series reconstruction approach employed for system identification.
6.2.1. System Response Dynamics:
Figure 6 illustrates the displacement time history of all three masses in the 3-DOF fractional-order system over a 200 s simulation period. The response exhibits distinct amplitude gradation across the three masses, with Mass 3 (dotted black line) demonstrating the largest displacement amplitude of approximately units. This enhanced response magnitude is attributable to the direct application of the external forcing function to this mass. Mass 2 (dashed red line) exhibits an intermediate amplitude of approximately units, while Mass 1 (solid blue line) shows the smallest oscillatory amplitude of approximately units. This progressive attenuation of response amplitude from Mass 3 to Mass 1 illustrates the characteristic energy transfer mechanism through the coupled fractional Duffing chain.
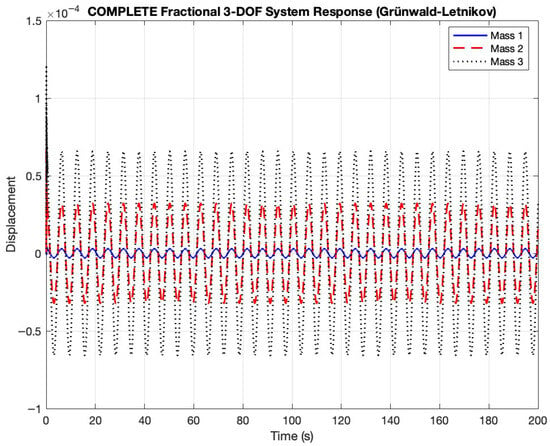
Figure 6.
Fractional system tesponse of 3-DOF Duffing system.
The steady-state response demonstrates perfectly periodic behavior throughout the entire simulation duration, indicating that the system has reached a stable forced response condition. The presence of fractional-order term (with derivative order ) manifests in the phase relationships between the three masses, creating a distinctive dynamic pattern that differs from classical integer-order systems. The system exhibits consistent oscillatory behavior with well-defined amplitude relationships that remain stable over the extended 200 s time span, confirming the effectiveness of the Grünwald–Letnikov implementation for long-duration fractional system simulations.
6.2.2. Fourier Reconstruction Validation:
Figure 7, Figure 8 and Figure 9 present comparisons between the original displacement signals and their Fourier series reconstructions for Masses 1, 2, and 3, respectively. These reconstructions employ a finite number of harmonic components to approximate the periodic steady-state responses, with a reconstruction error of 0.47% for each of the three masses.
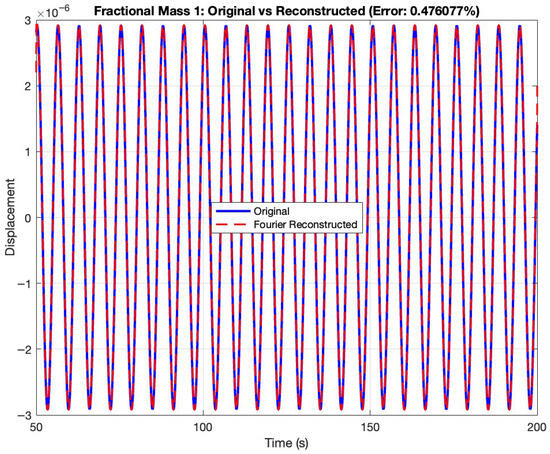
Figure 7.
Original vs. Fourier reconstructed displacement of Mass 1 for fractional Duffing oscillator.
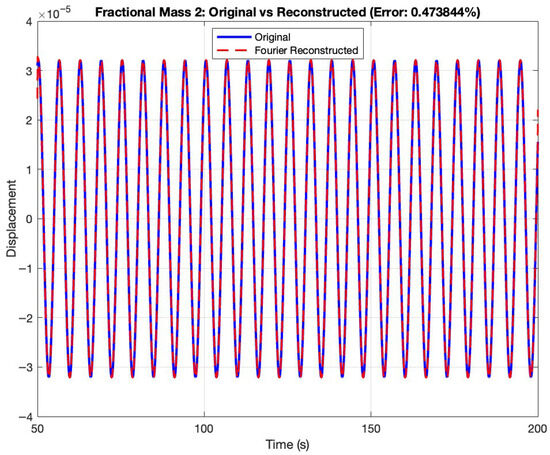
Figure 8.
Original vs. Fourier reconstructed displacement of Mass 2 for fractional Duffing oscillator.
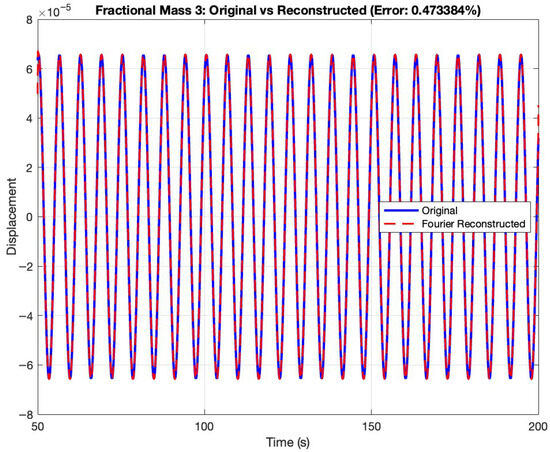
Figure 9.
Original vs. Fourier reconstructed displacement of Mass 3 for fractional Duffing oscillator.
In Figure 7, the original displacement of Mass 1 (solid blue line) and its Fourier reconstruction (dashed red line) demonstrate remarkable congruence throughout the simulation period from 50 to 200 s. The excellent agreement validates that despite the complex fractional-order dynamics, the steady-state response can be effectively represented using harmonic functions. The amplitude range of approximately units is faithfully captured by the Fourier series approximation, with an exceptionally low reconstruction error of 0.47%.
Similarly, Figure 8 exhibits excellent correlation between the original and reconstructed displacements for Mass 2. The Fourier reconstruction accurately reproduces both the amplitude (approximately units) and phase characteristics of the original signal, further confirming the efficacy of frequency domain analysis for this fractional-order system. The reconstruction error of 0.47% demonstrates the high fidelity of the harmonic approximation.
Figure 9 demonstrates comparable accuracy in reconstructing the displacement of Mass 3, which experiences the largest amplitude oscillations (approximately units) due to direct excitation. The precise correspondence between original and reconstructed signals indicates that the selected number of Fourier terms provides sufficient resolution to capture the dynamic behavior of the system accurately, achieving a reconstruction error of only 0.47%.
Figure 10 shows the validation of the fractional system identification applied to the 3-DOF Duffing oscillator, comparing original and identified acceleration signals for all three masses over the steady-state window (50–200 s). The identified responses closely follow the originals, yielding very low identification errors of , , and for Masses 1, 2, and 3, respectively. In the upper subplot, Mass 1 (least excited) displays accelerations on the order of with near-perfect amplitude and phase matching; the middle subplot (Mass 2) reaches approximately and similarly shows excellent agreement; and the lower subplot (Mass 3), which receives direct forcing and attains the largest accelerations (~), is reconstructed with comparably high fidelity. These consistently low errors corroborate several key strengths of the proposed frequency domain identification framework. They indicate that the Fourier reconstruction of fractional derivatives provides accurate basis functions, that the structured regressor matrix successfully captures coupled and memory-dependent dynamics, and that the pseudoinverse parameter estimation yields stable parameter estimates even in the presence of nonlinear coupling. Collectively, the results demonstrate the practical viability and computational efficiency of the method for extracting physical parameters from fractional-order mechanical systems.
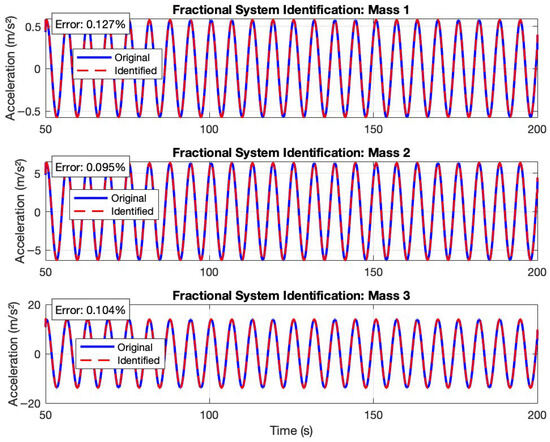
Figure 10.
Acceleration vs. time for fractional system identification for Mass 1, Mass 2, and Mass 3.
6.2.3. Performance Metrics
The individual mass identification errors achieved by the complete fractional system identification framework are noticeably low: for Mass 1, for Mass 2, and for Mass 3, yielding an average error of just . This outstanding performance reflects the high fidelity of the regressor matrices constructed from the Fourier-reconstructed kinematics and the Grünwald–Letnikov fractional derivatives. By discarding the initial 0– transient period—during which the system response includes nonperiodic startup dynamics—and focusing the analysis exclusively on the 50– steady-state window, the identification routine avoids contamination from exponentially decaying transients. As a result, the parameter estimation leverages only time-periodic data that satisfy the harmonic balance assumptions, thereby minimizing bias and improving the numerical conditioning of the pseudoinverse solution.
The fractional Fourier reconstruction validates the adequacy of the selected spectral resolution. Specifically, when 1000 Fourier terms are employed in the advanced reconstruction, the steady-state displacement responses of all three masses are recovered with sub-percent accuracy, yielding an average relative error of only for each mass. The large number of harmonics ensures that even relatively subtle spectral features induced by the fractional-order damping and nonlinear stiffness are faithfully represented, leading to smooth, noise-resilient reconstructions of position, velocity, acceleration, and fractional derivatives. Together, the removal of the transient portion and the adoption of a high-order Fourier basis combine to produce highly accurate regressor inputs and, consequently, to reduce the overall fractional system identification error to an noticeably low . Another important observation is that, for the single-degree-of-freedom (1-DOF) oscillator, the periodic steady-state response is primarily governed by the fundamental excitation frequency, with additional contributions from a limited number of higher harmonics arising due to the cubic nonlinearity. In this case, truncating the Fourier series to harmonics captures virtually all of the significant spectral content—higher-order harmonics beyond the tenth contribute negligibly to the signal-energy and their omission introduces reconstruction errors well below 1%. By contrast, the three-degree-of-freedom (3-DOF) system exhibits richer modal interactions and coupling harmonics among the three masses. Its steady-state response therefore contains a much denser spectrum of frequency components, both at the excitation frequency and at combination harmonics arising from nonlinear coupling. To resolve this more complex spectrum over the long analysis window (50–200 s), the advanced Fourier method employs 1000 terms, ensuring that all relevant harmonics—and the fine spectral features induced by fractional damping and inter-mass coupling—are retained. This high harmonic count yields sub-percent reconstruction errors (≈0.47%) and enables the equally low identification errors (≈0.10%) reported for the 3-DOF system.
6.2.4. Theoretical Implications:
The exceptionally precise Fourier reconstructions across all three masses substantiate several important theoretical aspects of fractional-order systems. First, they confirm that despite the nonlocal nature of fractional derivatives and their inherent memory effects, the steady-state forced response maintains periodicity that is amenable to Fourier analysis. Second, they demonstrate that a finite number of harmonic components is sufficient to represent the dynamics of the fractional-order system with high accuracy. This finding has significant implications for system identification and model reduction techniques in fractional-order mechanical systems.
The results illustrate the effectiveness of combining fractional calculus with traditional frequency domain analysis methods, providing a powerful approach for characterizing complex mechanical systems that exhibit non-classical damping behavior. This methodology bridges the gap between the mathematical complexity of fractional-order models and practical engineering applications requiring accurate system identification.
6.3. Identification of System Parameters in the Presence of Noise
System parameters can be correctly identified in the presence of noise disturbances, but with reduced accuracy and requiring specialized robust techniques [27,34]. For fractional-order systems such as Duffing oscillators, noise poses particular challenges because fractional derivatives computed via the Grünwald–Letnikov formulation are inherently sensitive to high-frequency disturbances: the convolutional (memory) nature of the GL operator causes past noisy samples to influence current derivative estimates, amplifying high-frequency contamination [1,48,49]. The Fourier-based harmonic reconstruction employed in this study provides natural noise suppression by truncating high-frequency content (here ), which filters out much of the noise prior to derivative reconstruction [19,51]; nonetheless, noise still degrades identification through contamination of the regressor matrix Q, amplification during numerical differentiation for velocity and acceleration reconstruction, and accumulation of errors in the pseudoinverse estimation [34]. To preserve acceptable identification performance, practitioners therefore employ robust strategies such as Tikhonov (ridge) regularization , ensemble averaging over multiple periods, preprocessing with low-pass filters, and increasing data length to improve SNR; these measures are standard in system identification and fractional model estimation workflows [27,34,57]. Under ideal, low-noise conditions, the paper reports parameter errors on the order of , while realistic noise levels (SNR dB) typically increase errors (often to ), with fractional parameters being especially sensitive due to long-memory effects [1,27].
7. Discussion
This research presents a rigorous and computationally efficient methodology for identifying parameters in fractional-order mechanical systems, with a particular focus on the fractional Duffing oscillator. By leveraging the GL characterization of fractional derivatives and employing Fourier series-based reconstruction of steady-state responses, we establish a linear regression framework capable of accurately estimating both linear and nonlinear system parameters, including fractional damping coefficients, without requiring iterative optimization. The results demonstrate that the method reliably recovers key physical parameters from simulated data, with normalized estimation errors remaining below . Comparative analyses between original and reconstructed signals in both time and phase domains confirm that the Fourier-based approach preserves the core dynamic features of the underlying system, including its nonlinearities and fractional-order effects.
In addition to single-degree-of-freedom analysis, the study extends to a three-degree-of-freedom (3-DOF) fractional Duffing system, providing deeper insights into the interplay between memory-dependent damping and multi-body dynamics. The introduction of fractional-order derivatives () fundamentally alters the energy dissipation mechanisms, introducing nonlocal memory effects that produce distinctive attenuation profiles across the coupled oscillators. Simulations reveal a consistent amplitude decay from the point of excitation, highlighting the directional energy transfer properties intrinsic to fractional systems. Importantly, the system retains perfectly periodic responses under harmonic excitation, validating the applicability of classical frequency domain methods to fractional-order models. The success of the truncated Fourier series in capturing these dynamics underscores the potential of low-dimensional harmonic representations for efficient modeling and system identification in such settings.
The parameter estimation framework employs a minimal input–output configuration in which the input is a known harmonic excitation force—specifically, applied to the single mass in the 1-DOF system ( rad/s) or exclusively to the third mass in the 3-DOF system ( rad/s and N), while the remaining masses are unforced—and the outputs require only displacement measurements for the 1-DOF case or for the 3-DOF case. The central innovation is a Fourier-based signal-processing pipeline that reconstructs all additional signals required for identification (velocity , acceleration , fractional derivatives using a Grünwald–Letnikov discretization, nonlinear terms such as , and coupling terms and their derivatives) from displacement-only measurements, and then assembles these reconstructed signals into structured regressor matrices Q for pseudoinverse estimation [1,27,51]. The GL formulation is particularly convenient for the discrete time implementation of the fractional derivative and its convolutional memory structure is well suited to the long-duration, steady-state simulations used here [1,48,49].
The selection of the number of Fourier terms M must balance reconstruction fidelity against computational cost: the required M increases with the degree of nonlinearity (more harmonics generated by stronger nonlinearities), with fractional order closer to unity, and with the proximity of forcing frequency to resonances; a practical procedure is to conduct a convergence study by incrementing M from a base (e.g., and monitoring reconstruction metrics such as normalized RMSE or retained spectral energy from an FFT, increasing M until the error falls below a target tolerance (e.g., <1%) or until the retained energy exceeds a chosen threshold (e.g., 95–99%) [19,51,58]. In the present 3-DOF fractional Duffing examples, was found to be sufficient for high-fidelity reconstruction; however, less complex systems may necessitate –20. Importantly, the choice of M directly affects the size and conditioning of the regressor Q and thus the numerical stability of the pseudoinverse-based parameter estimation [27,34].
The combined framework of GL-based numerical simulation and Fourier domain analysis offers a powerful toolset for understanding and controlling fractional-order mechanical systems. Despite the inherent computational intensity of fractional calculus, this study demonstrates that accurate, interpretable, and scalable solutions are achievable. The presented methods are not only theoretically robust but also well-suited for experimental implementation in systems exhibiting viscoelasticity, distributed parameter dynamics, or anomalous damping. Future work may focus on extending the framework to systems with multiple fractional orders, exploring alternative formulations of fractional derivatives, and validating the approach through real-world experimental setups. Furthermore, we shall also treat the fractional order as an unknown model parameter to be estimated from the steady-state response. By augmenting the parameter vector to include , our identification framework will simultaneously calibrate both the classical physical coefficients and the degree of memory-dependent damping, thereby yielding a fully data-driven determination of the system’s hereditary dynamics. Hence, this work contributes significantly to the ongoing integration of fractional calculus into practical engineering domains, offering a pathway toward more realistic and predictive models of complex dynamical systems.
It is known that nonlinear systems may exhibit complex chaotic behavior. Therefore, system parameter identification in chaotic regimes presents fundamental challenges. However, it remains feasible using specialized nonlinear techniques, although the Fourier-based harmonic reconstruction methods developed in our study are not directly applicable to such regimes. Chaotic systems exhibit bounded but not periodic behavior and present sensitive dependence on initial conditions, so they lack the stable periodic structure required for frequency domain regression; consequently, small parameter variations can produce vastly different trajectories, rendering standard least-squares methods unreliable [20,59]. Instead, chaotic identification typically relies on nonlinear time series tools such as state-space reconstruction via delay embedding (to recover the attractor geometry) [59,60], Lyapunov exponent estimation to quantify instability and sensitivity [61], and synchronization- or observer-based techniques in which a model is driven to synchronize with the observed system and parameters are adjusted to minimize synchronization error [62,63,64]. These approaches are complemented by specialized nonlinear optimization and validation procedures from the system identification literature [34], and they have been extended in various ways to accommodate fractional-order dynamics and transfer function estimation in the frequency domain [27]. The present paper acknowledges this limitation, noting that while the fractional Duffing model can exhibit period doubling and chaotic behavior, the proposed framework focuses on steady-state harmonic responses and suggests future work aimed at bifurcation analysis to explore roads to chaos; thus, identification in chaotic regimes will require different methods than those presented here [20,27].
Fractional-order identification methods based on operational matrices—such as Haar wavelet and block-pulse schemes—offer strong time–frequency localization and computational simplicity but exhibit notable limitations for steady-state, frequency domain identification. Haar wavelet operational matrix approximations use piecewise-constant bases that introduce discontinuities and spurious high-frequency content, resulting in poor frequency resolution and accumulated approximation error for long-duration harmonic signals [28]. Block-pulse operational matrix methods likewise suffer from coarse spectral resolution and abrupt basis transitions, which introduce spurious harmonics and yield ill-conditioned regressors when modeling smooth periodic responses [65]. Consequently, both approaches often yield biased parameter estimates and reduced numerical stability compared with frequency domain techniques. In contrast, the Grünwald–Letnikov (GL) characterization, when integrated with Fourier domain reconstruction as employed in the present work, exhibits a natural consistency with harmonic balance principles while effectively eliminating basis-induced artifacts. In particular, as shown in our work, by projecting steady-state displacement onto a truncated Fourier basis and reconstructing velocity, acceleration, and fractional derivatives in the frequency domain, the Fourier–GL pipeline produces smooth, analytically consistent derivative estimates. It allows to preserve long-memory power law behavior while maintaining favorable conditioning of the regression matrices, as also mentioned in [18,19,20,66]. Hence, our approach enables direct pseudoinverse estimation of modal mass, stiffness, classical damping, and fractional coefficients in a single step, achieving sub-percent identification errors under ideal conditions—performance levels typically unattainable by Haar or block-pulse operational matrix schemes [14].
Although this paper has focused on Fourier-based identification of steady-state parameters, the underlying fractional Duffing model also exhibits rich nonlinear phenomena, such as period-doubling and chaos, which can be conveniently explored via bifurcation diagrams. In particular, the numerical integration scheme proposed by Yuan and Agrawal [19] for fractional-derivative systems could be employed to trace changes in the system’s periodic solutions as key parameters (e.g. forcing amplitude F or fractional order are varied. Such a bifurcation analysis would complement our Fourier-based steady-state identification by revealing the stability boundaries and transitions between qualitatively different oscillatory regimes. We therefore plan, in future work, to also adapt the DETC’98 algorithm to generate parameterized bifurcation diagrams for the fractional Duffing oscillator, deepening our understanding of how fractional damping shapes the onset of complex dynamics. In addition, a fully fractional model of the Duffing oscillator will be investigated to examine its dynamical behavior. A comparative analysis between this model and the proposed formulation will be conducted, thereby providing deeper insights into the intricate dynamics associated with fractional derivatives.
Moreover, in the future, extending the present framework to fractional-order systems with presents both significant theoretical opportunities and substantial computational challenges that merit systematic study. When the fractional order exceeds unity, models can exhibit fundamentally different behavior–including enhanced, long-range memory effects and a physical interpretation that shifts from purely dissipative memory to inertial memory (history-dependent inertial forces)–a perspective greatly discussed in foundational fractional model literature [1,26,67]. These changes produce altered stability conditions and may generate richer nonlinear dynamics, with new bifurcation scenarios and chaotic regimes not typically observed for sub-unity orders; such phenomena have been linked to anomalous transport and super-diffusive regimes in continuum models. From a numerical viewpoint, implementing requires careful attention to time discretisation and truncation. Standard Grünwald–Letnikov (GL) discretizations must be re-examined for stability and accuracy when the weight decay is slower (the asymptotic decay rate depends on ), so shifted Grünwald and weighted-second-order Grünwald (WSGD)-type schemes or other stabilized approximations are often employed to recover stability and higher-order convergence [68,69]. For robust time stepping, convolution quadrature methods provide a principled route to stable discretization of history integrals and are therefore recommended for stiff inertial-type fractional terms [70]. Practically, models lead to increased memory storage demands (slower coefficient decay yields a longer effective memory horizon) and stricter convergence conditions for truncated series; these affect computational cost and necessitate tailored truncation/tolerance criteria. Moreover, Fourier domain reconstruction and transfer function approaches must be adapted to account for modified phase relationships and potential multi-valued frequency responses arising from higher fractional orders. Finally, parameter identification becomes more ill-conditioned for , and successful identification requires specialized regularization and identification strategies developed for fractional models [27,71]. Collectively, these extensions would broaden the applicability of fractional-order modeling to capture super-diffusive transport, accelerating creep and memory-enhanced inertial effects in advanced materials and biological systems [26].
Author Contributions
Conceptualization, D.D., M.P. and J.J.L.; methodology, D.D.; software, D.D.; validation, I.T., J.J.L. and D.D.; formal analysis, D.D.; investigation, D.D.; resources, D.D.; data curation, D.D.; writing—original draft preparation, D.D.; writing—review and editing, D.D. and I.T.; visualization, D.D.; supervision, I.T., J.J.L., M.P. and T.S.; project administration, T.S.; funding acquisition, I.T. and T.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been accomplished with financial support by the European Regional Development Fund within the Operational Programme “Bulgarian national recovery and resilience plan”, for direct provision of grants “Establishing of a network of research higher education institutions in Bulgaria”, and under Project BG-RRP-2.004-0005 “Improving the research capacity and quality to achieve intErnAtional recognition and reSilience of TU-Sofia (IDEAS)”.
Data Availability Statement
No new data was created or analyzed in this study.
Acknowledgments
We would like to express our sincere gratitude to the reviewers for their invaluable and insightful comments, which have greatly facilitated the revision of this paper and contributed to enhancing its overall quality.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Chakraverty, S.; Jena, R.M.; Jena, S.K. Computational Fractional Dynamical Systems: Fractional Differential Equations and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2022. [Google Scholar]
- Chen, Y.; Moore, K.L. Fractional order control—A tutorial. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 1397–1411. [Google Scholar]
- Mainardi, F. Fractional calculus: Some basic problems in continuum and statistical mechanics. Fractals Fract. Calc. Contin. Mech. 1997, 378, 291–348. [Google Scholar]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists; World Scientific: Singapore, 2011. [Google Scholar]
- Chen, B.; Li, C.; Wilson, B.; Huang, Y. Fractional Modeling and Analysis of Coupled MR Damping System. IEEE/CAA J. Autom. Sin. 2016, 3, 288–294. [Google Scholar] [CrossRef]
- Noël, J.P.; Kerschen, G. Nonlinear vibration modes of symmetric and asymmetric systems: Theory and applications. Mech. Syst. Signal Process. 2015, 74, 18–36. [Google Scholar]
- Mikhlin, Y.; Avramov, K.V. Nonlinear Normal Modes of Vibrating Mechanical Systems: 10 Years of Progress. Appl. Mech. Rev. 2024, 76, 050801. [Google Scholar] [CrossRef]
- Tang, Y.; Peng, Y.; He, G.; Liang, W.; Zhang, W. P-Bifurcation Analysis for a Fractional Damping Stochastic Nonlinear Equation with Gaussian White Noise. Fractal Fract. 2023, 7, 408. [Google Scholar] [CrossRef]
- Li, G.; Xie, R.; Yang, H. Study on fractional-order coupling of high-order Duffing oscillator and its application. Chaos Solitons Fractals 2024, 186, 115255. [Google Scholar] [CrossRef]
- Baleanu, D.; Sajjadi, S.S.; Jajarmi, A.; Defterli, Ö. On a nonlinear dynamical system with both chaotic and nonchaotic behaviors: A new fractional analysis and control. Adv. Differ. Equ. 2021, 2021, 234. [Google Scholar] [CrossRef]
- Qian, K.; Tian, L.; Bao, J. Frequency-domain physical constrained neural network for nonlinear system dynamic prediction. Eng. Appl. Artif. Intell. 2023, 122, 106127. [Google Scholar] [CrossRef]
- Breunung, T.; Balachandran, B. Frequency response based identification of nonlinear oscillators. J. Sound Vib. 2025, 594, 118651. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, C.; Lai, S.-K.; Chen, Z.; Chen, L. Frequency-dependent equivalent impedance analysis for optimizing vehicle inertial suspensions. Nonlinear Dyn. 2025, 113, 9373–9398. [Google Scholar] [CrossRef]
- Franczyk, B.; Maniowski, M.; Gołdasz, J. Frequency-dependent automotive suspension damping systems: State of the art review. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 238, 2491–2503. [Google Scholar] [CrossRef]
- Al-Souqi, K.; Kadri, K.; Emam, S. A Review on Vibration Control Using Piezoelectric Shunt Circuits. Appl. Sci. 2025, 15, 6035. [Google Scholar] [CrossRef]
- Franczyk, B.; Gołdasz, J. Modelling and experimental study of a passive frequency-dependent vehicle suspension damper. Acta Mech. Et Autom. 2024, 18, 409–418. [Google Scholar] [CrossRef]
- Tuwa, P.R.N.; Molla, T.; Noubissie, S.; Kingni, S.T.; Rajagopal, K. Analysis of a quarter car suspension based on a Kelvin–Voigt viscoelastic model with fractional-order derivative. Int. J. -Non-Linear Mech. 2021, 137, 103818. [Google Scholar] [CrossRef]
- Sofi, A. Nonlinear vibrations of beams with fractional derivative elements crossed by moving loads. Int. J. -Non-Linear Mech. 2024, 159, 104567. [Google Scholar] [CrossRef]
- Han, Y.X.; Zhang, J.X.; Wang, Y.L. Dynamic behavior of a two-mass nonlinear fractional-order vibration system. Front. Phys. 2024, 12, 1452138. [Google Scholar] [CrossRef]
- Yang, X.; Zeng, S.; Liu, C.; Liu, X.; Wang, Z.; Yang, Y. Optimal design and performance evaluation of HMDV inertial suspension based on generalized skyhook control. Int. J. Struct. Stab. Dyn. B 2025, 25, 2550069. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, C.; Zheng, X.; Zhao, L.; Qiu, Y. Advancements in semi-active automotive suspension systems with magnetorheological dampers: A review. Appl. Sci. 2024, 14, 7866. [Google Scholar] [CrossRef]
- Kimball, J.B.; DeBoer, B.; Bubbar, K. Adaptive control and reinforcement learning for vehicle suspension control: A review. Annu. Rev. Control 2024, 58, 100974. [Google Scholar] [CrossRef]
- Yu, M.; Evangelou, S.A.; Dini, D. Advances in active suspension systems for road vehicles. Engineering 2024, 33, 160–177. [Google Scholar] [CrossRef]
- Koeller, R. Applications of Fractional Calculus to the Theory of Viscoelasticity. J. Appl. Mech. 1984, 51, 299–307. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; World Scientific: Singapore, 2022. [Google Scholar]
- Valério, D.; Sá da Costa, J.S. Identifying Digital and Fractional Transfer Functions from a Frequency Response. Int. J. Control 2011, 84, 445–457. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, W. Haar wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations. Appl. Math. Comput. 2010, 216, 2276–2285. [Google Scholar] [CrossRef]
- Guariglia, E.; Guido, R.C.; Dalalana, G.J. From Wavelet Analysis to Fractional Calculus: A Review. Mathematics 2023, 11, 1606. [Google Scholar] [CrossRef]
- Li, Y.; Sun, N. Numerical Solution of Fractional Differential Equations Using the Generalized Block Pulse Operational Matrix. Comput. Math. Appl. 2011, 62, 1046–1054. [Google Scholar] [CrossRef]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods; Courier Corporation: Mumbai, India, 2001. [Google Scholar]
- Shen, J.; Tang, T.; Wang, L.L. Spectral Methods: Algorithms, Analysis and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 41. [Google Scholar]
- Fornberg, B. A Practical Guide to Pseudospectral Methods; Cambridge University Press: Cambridge, UK, 1998; Volume 1. [Google Scholar]
- Ljung, L.; Glad, T.; Hansson, A. Modeling and Identification of Dynamic Systems; Studentlitteratur: Lund, Sweden, 2021. [Google Scholar]
- Scherer, R.; Kalla, S.L.; Tang, Y.; Huang, J. The Grünwald–Letnikov method for fractional differential equations. Comput. Math. Appl. 2011, 62, 902–917. [Google Scholar] [CrossRef]
- Macías-Díaz, J.E. Fractional calculus—Theory and applications. Axioms 2022, 11, 43. [Google Scholar] [CrossRef]
- Naifar, O.; Makhlouf, A.B. Fractional Order Systems—Control Theory and Applications; Springer International Publishing: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Duffing, G.W.C. Erzwungene Schwingungen bei veräNderlicher Eigenfrequenz; F. Vieweg: Braunschweig, Germany, 1918. [Google Scholar]
- Li, Z.L.; Sun, D.G.; Han, B.H.; Sun, B.; Zhang, X.; Meng, J.; Liu, F.X. Response of viscoelastic damping system modeled by fractional viscoelastic oscillator. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 3169–3180. [Google Scholar] [CrossRef]
- Ortiz, A.; Yang, J.; Coccolo, M.; Seoane, J.M.; Sanjuán, M.A. Fractional damping enhances chaos in the nonlinear Helmholtz oscillator. Nonlinear Dyn. 2020, 102, 2323–2337. [Google Scholar] [CrossRef]
- Agila, A.; Baleanu, D. A study of multi-degree of freedom fractional order damped oscillatory system. Upb Sci. Bull. Ser. D 2018, 80, 52–62. [Google Scholar]
- Narayanan, M.D.; Narayanan, S.; Padmanabhan, C. Parametric identification of nonlinear systems using multiple trials. Nonlinear Dyn. 2007, 48, 341–360. [Google Scholar] [CrossRef]
- Failla, G.; Zingales, M. Advanced materials modelling via fractional calculus: Challenges and perspectives. Philos. Trans. R. Soc. A 2020, 378, 20200050. [Google Scholar] [CrossRef]
- Bahloul, M.A.; Aboelkassem, Y.; Belkhatir, Z.; Laleg-Kirati, T.M. Fractional-Order Modeling of Arterial Compliance in Vascular Aging: A Computational Biomechanical Approach for Investigating Cardiovascular Dynamics. IEEE Open J. Eng. Med. Biol. 2023, 5, 650–660. [Google Scholar] [CrossRef]
- Li, Z.; Chen, D.; Zhu, J.; Liu, Y. Nonlinear dynamics of fractional order Duffing system. Chaos, Solitons Fractals 2015, 81, 111–116. [Google Scholar] [CrossRef]
- Khader, M.M.; Kumar, S. An efficient computational method for solving a system of FDEs via fractional finite difference method. Appl. Appl. Math. Int. J. (Aam) 2019, 14, 32. [Google Scholar]
- Das, D.; Taralova, I.; Loiseau, J.J. Time-delay feedback control of fractional chaotic Rössler oscillator. Ifac-Papersonline 2024, 58, 90–95. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. The Analysis of Fractional Differential Equations; Lecture notes in mathematics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Meerschaert, M.M.; Tadjeran, C. Finite difference approximations for fractional advection–dispersion flow equations. J. Comput. Appl. Math. 2004, 172, 65–77. [Google Scholar] [CrossRef]
- Chang, Y.; Zhu, Y.; Li, Y.; Wang, M. Dynamical analysis of a fractional-order nonlinear two-degree-of-freedom vehicle system by incremental harmonic balance method. J. Low Freq. Noise, Vib. Act. Control 2024, 43, 706–728. [Google Scholar] [CrossRef]
- Yan, Z.; Dai, H.; Wang, Q.; Atluri, S.N. Harmonic Balance Methods: A Review and Recent Developments. Comput. Model. Eng. Sci. 2023, 137, 1419–1459. [Google Scholar] [CrossRef]
- Koç, E.; Koç, A. Fractional Fourier Transform in Time Series Prediction. IEEE Signal Process. Lett. 2022, 29, 2542–2546. [Google Scholar] [CrossRef]
- Cui, R.; Wei, Y.; Chen, Y.; Cheng, S.; Wang, Y. An Innovative Parameter Estimation for Fractional-Order Systems in the Presence of Outliers. Nonlinear Dyn. 2017, 89, 453–463. [Google Scholar] [CrossRef]
- Mani, A.K.; Narayanan, M.D.; Sen, M. Parametric Identification of Fractional-Order Nonlinear Systems. Nonlinear Dyn. 2018, 93, 945–960. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Tian, W.; Zhou, H.; Deng, W. A class of second order difference approximations for solving space fractional diffusion equations. Math. Comput. 2015, 84, 1703–1727. [Google Scholar] [CrossRef]
- Alqahtani, A.; Mach, T.; Reichel, L. Solution of ill-posed problems with Chebfun. Numer. Algorithms 2023, 92, 2341–2364. [Google Scholar] [CrossRef]
- Oppenheim, A.V. Discrete-Time Signal Processing; Pearson Education India: Noida, India, 1999. [Google Scholar]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warwick, Proceedings of the a Symposium Held at the University of Warwick, Berlin/Heidelberg, Germany, 7 October 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 366–381. [Google Scholar]
- Sauer, T.; Yorke, J.A.; Casdagli, M. Embedology. J. Stat. Phys. 1991, 65, 579–616. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821. [Google Scholar] [CrossRef]
- Abarbanel, H. Analysis of Observed Chaotic Data; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Parlitz, U. Estimating model parameters from time series by autosynchronization. Phys. Rev. Lett. 1996, 76, 1232–1235. [Google Scholar] [CrossRef]
- Momtahan, S.; Saeedi, H.; Moghaddam, M.M. A fractional block pulse operational method for solving a class of fractional partial differential equations. J. Fract. Calc. Appl. 2017, 8, 166–181. [Google Scholar]
- Li, L.; Wang, D. Numerical stability of Grünwald–Letnikov method for time fractional delay differential equations. Bit Numer. Math. 2021, 62, 995–1027. [Google Scholar] [CrossRef]
- Jin, B. Fractional Differential Equations; Springer International Publishing: Cham, Switzerland, 2010. [Google Scholar]
- Mirzaee, F.; Sayevand, K.; Rezaei, S.; Samadyar, N. Finite Difference and Spline Approximation for Solving Fractional Stochastic Advection-Diffusion Equation. Iran. J. Sci. Technol. Trans. A Sci. 2021, 45, 607–617. [Google Scholar] [CrossRef]
- Zhang, C.H.; Yu, J.W.; Wang, X. A Fast Second-Order Scheme for Nonlinear Riesz Space-Fractional Diffusion Equations. Numer. Algorithms 2023, 92, 1813–1836. [Google Scholar] [CrossRef]
- Ren, H.; Ma, J.; Liu, H. A Convolution Quadrature Using Derivatives and Its Application. Bit Numer. Math. 2024, 64, 8. [Google Scholar] [CrossRef]
- Valério, D.; Sá da Costa, J.S. Identifying Fractional Models from Frequency and Time Responses. In Proceedings of the 3rd IFAC Workshop on Fractional Differentiation and Its Applications, Ankara, Turkey, 5–7 November 2008. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).