Fractional Poisson Process for Estimation of Capacity Degradation in Li-Ion Batteries by Walk Sequences
Abstract
1. Introduction
2. Long-Range Dependence and Poisson Distribution
2.1. Long-Range Dependence
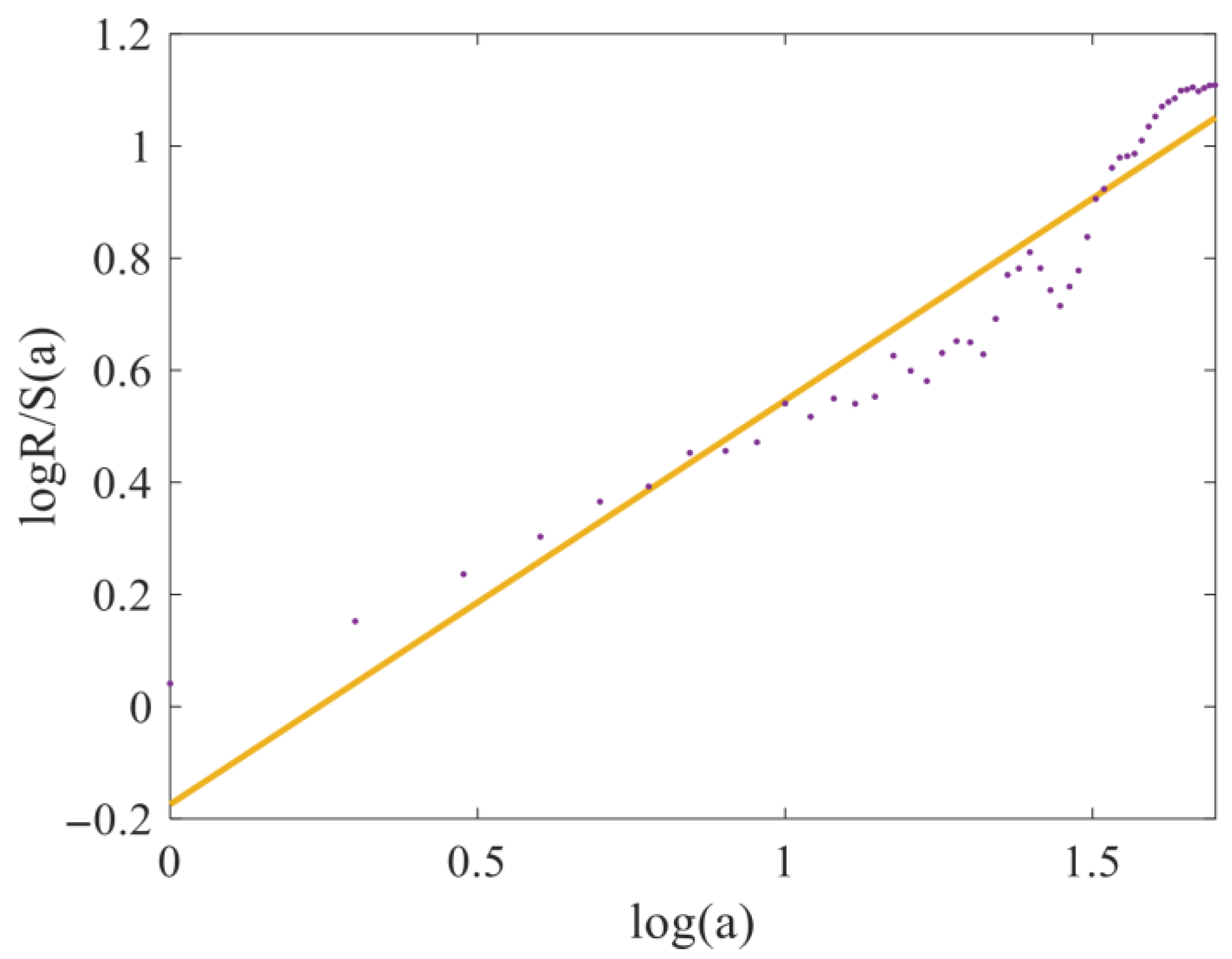
2.2. Estimation of the Hurst Exponent
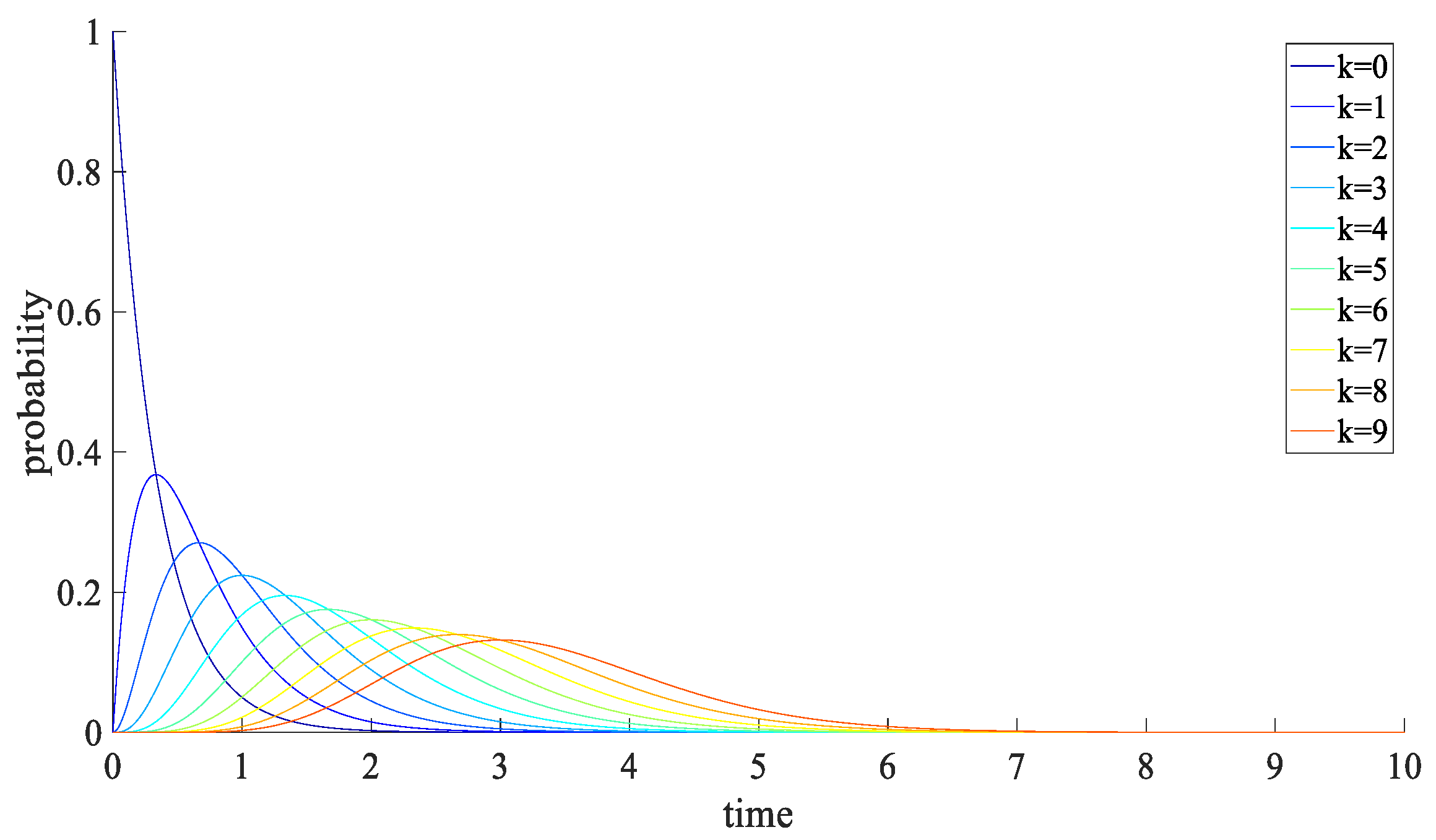
2.3. Sudden-Jump Characteristics of Poisson Distribution
2.4. Characteristics of a Random Walk
3. Definition and Characteristics of the Fractional Poisson Process
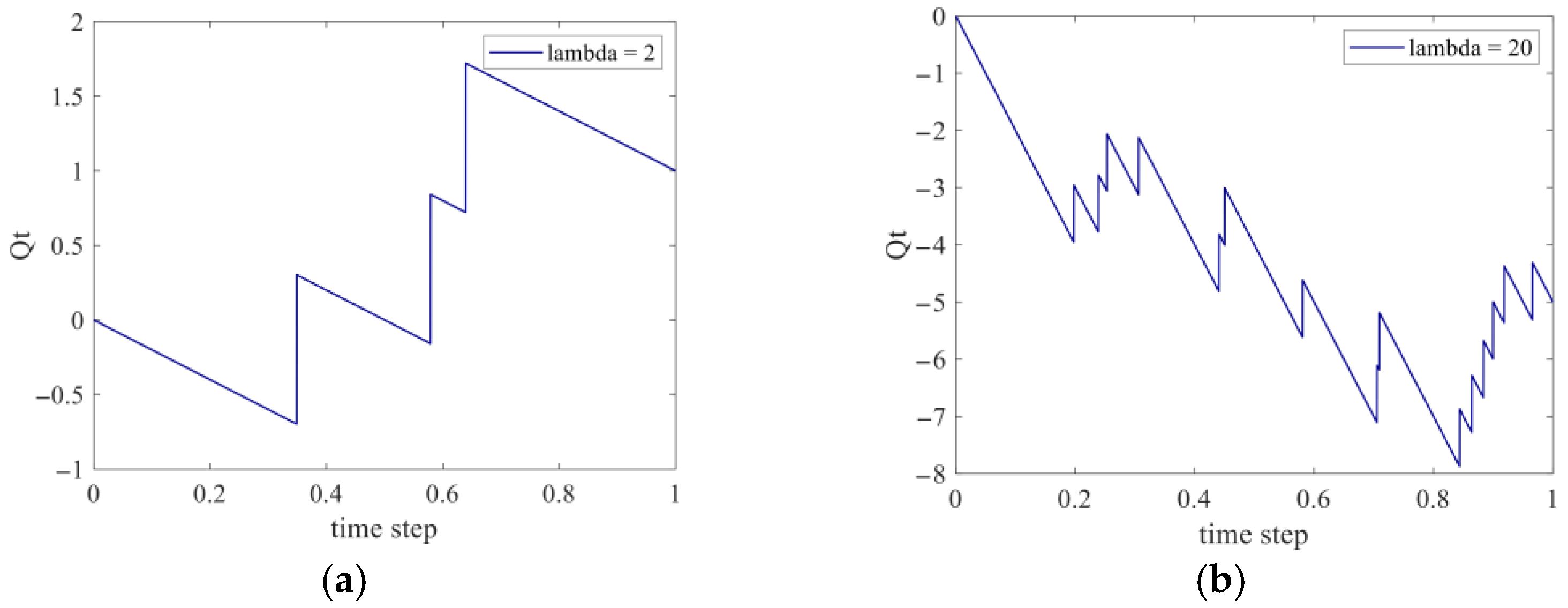
4. Fractional Poisson Process Predictive Model
5. Parameter Estimation
5.1. Estimation of Drift and Diffusion Coefficients
5.2. Estimation of the Rate of the Process
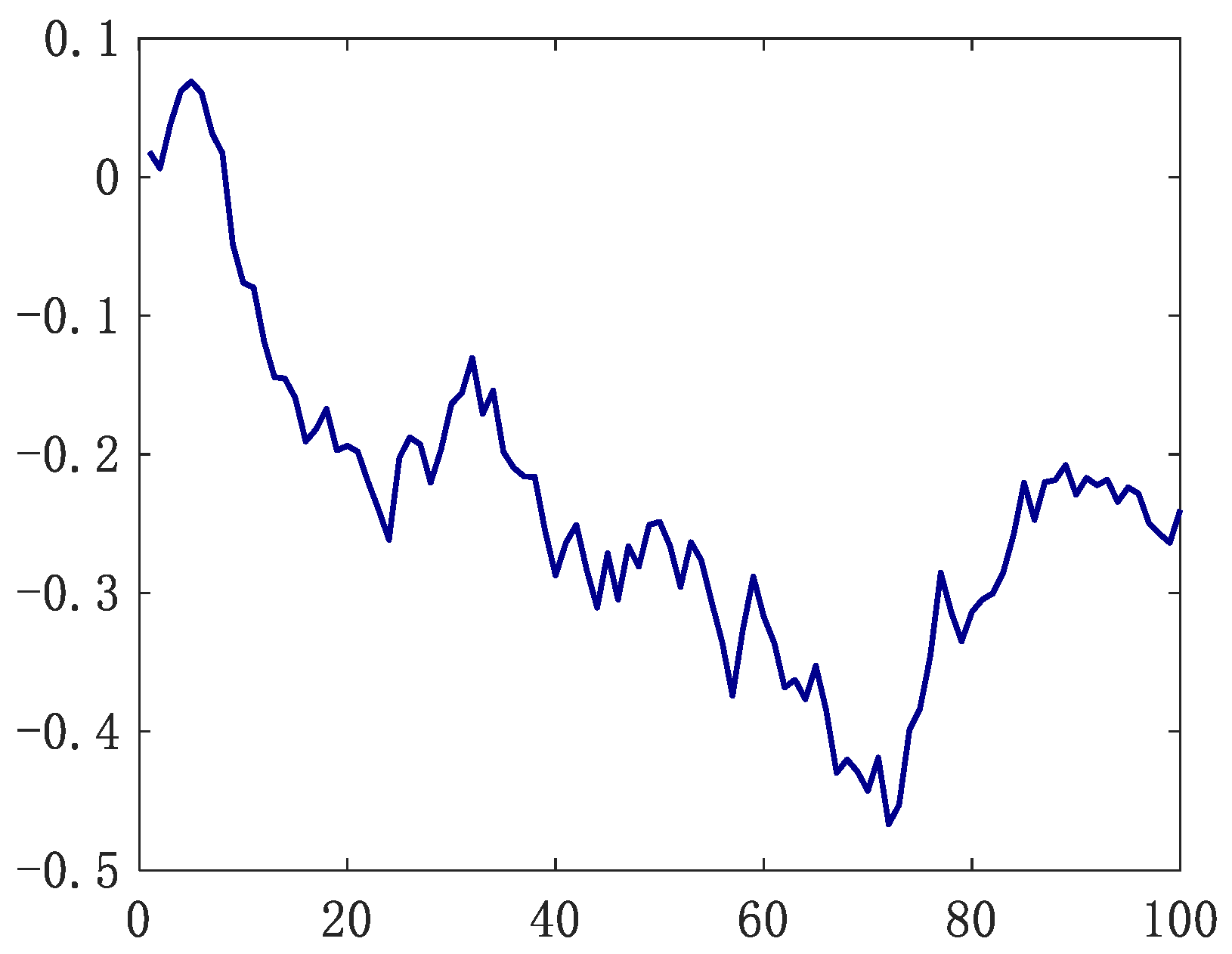
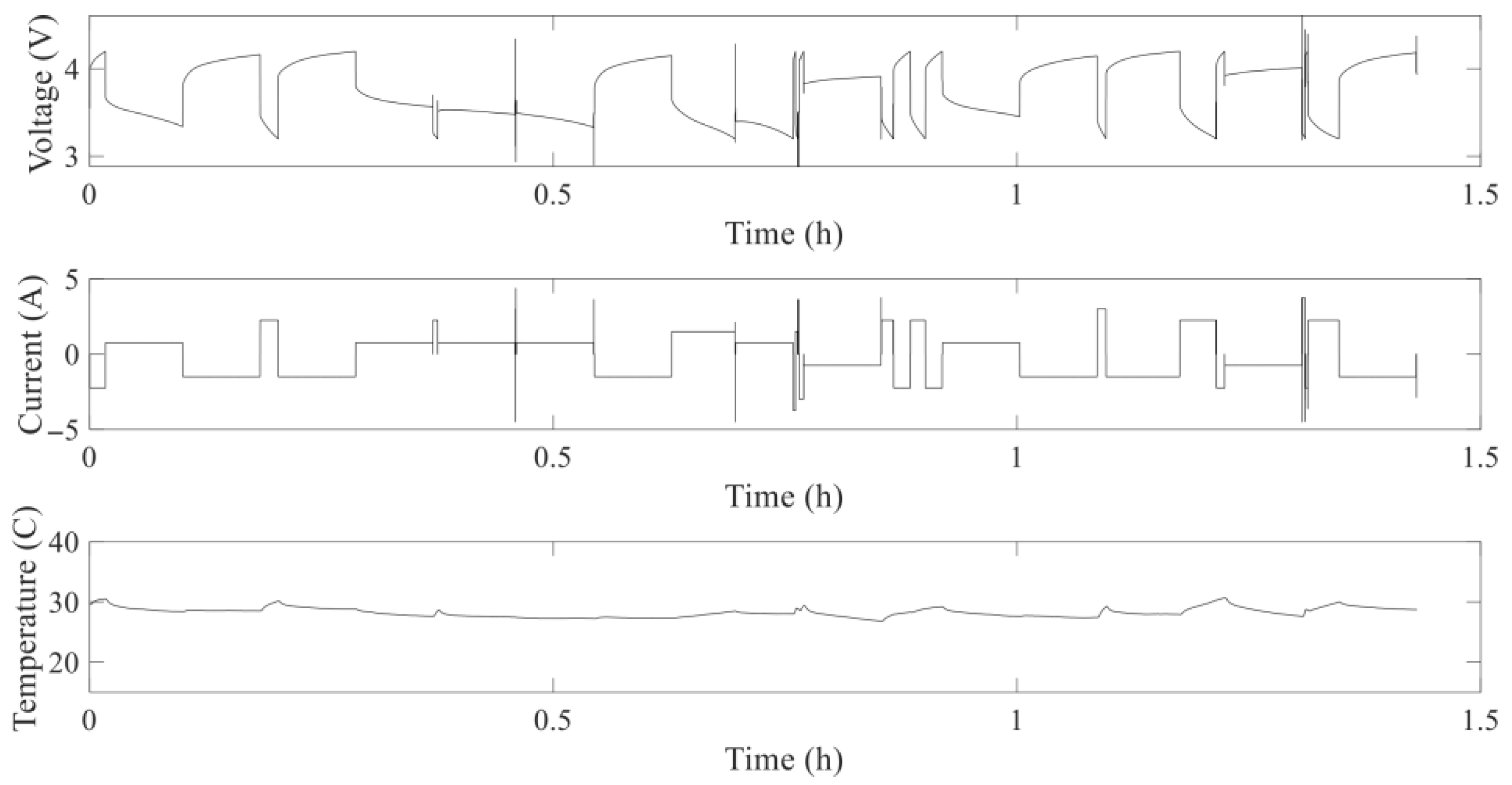
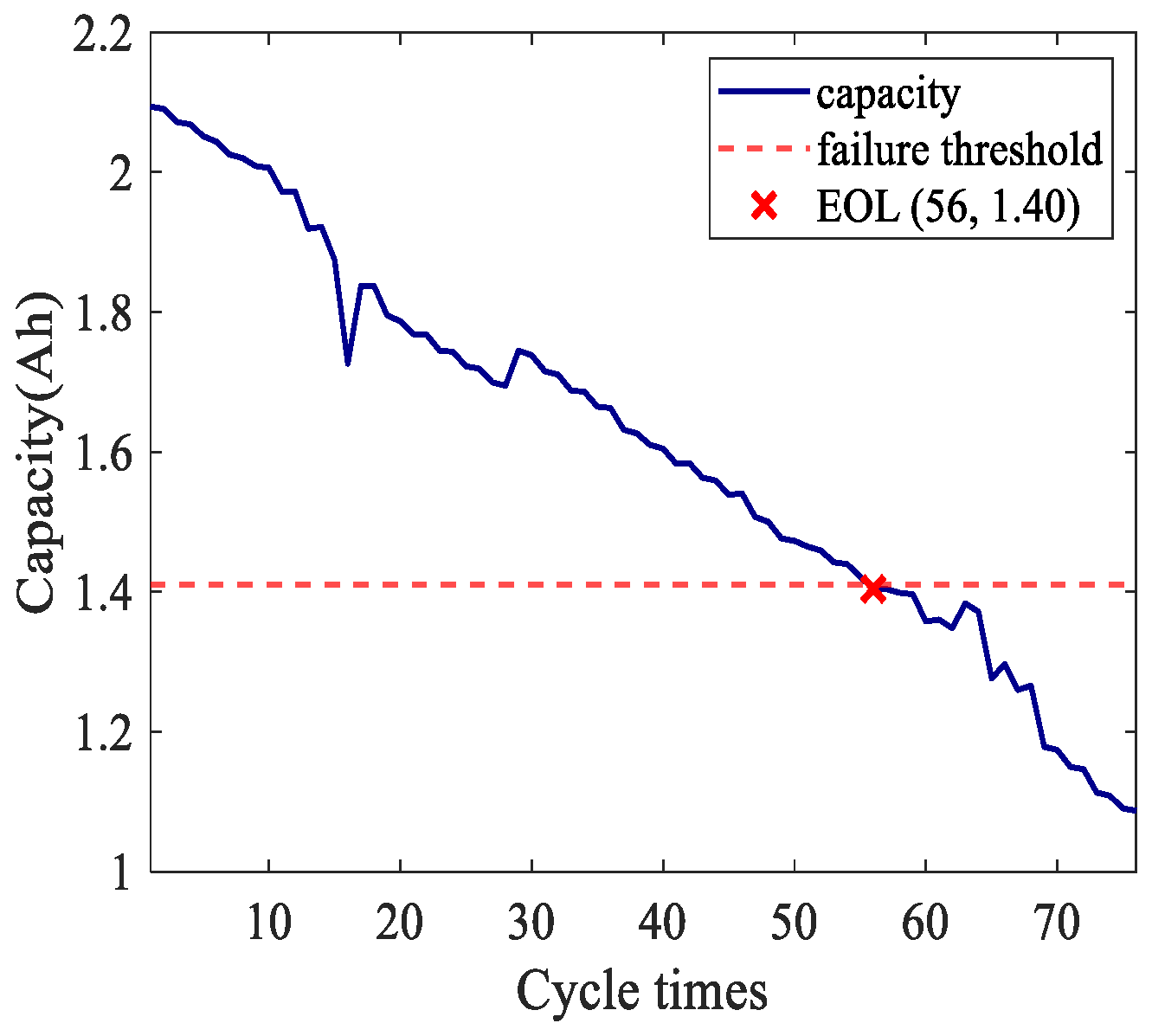
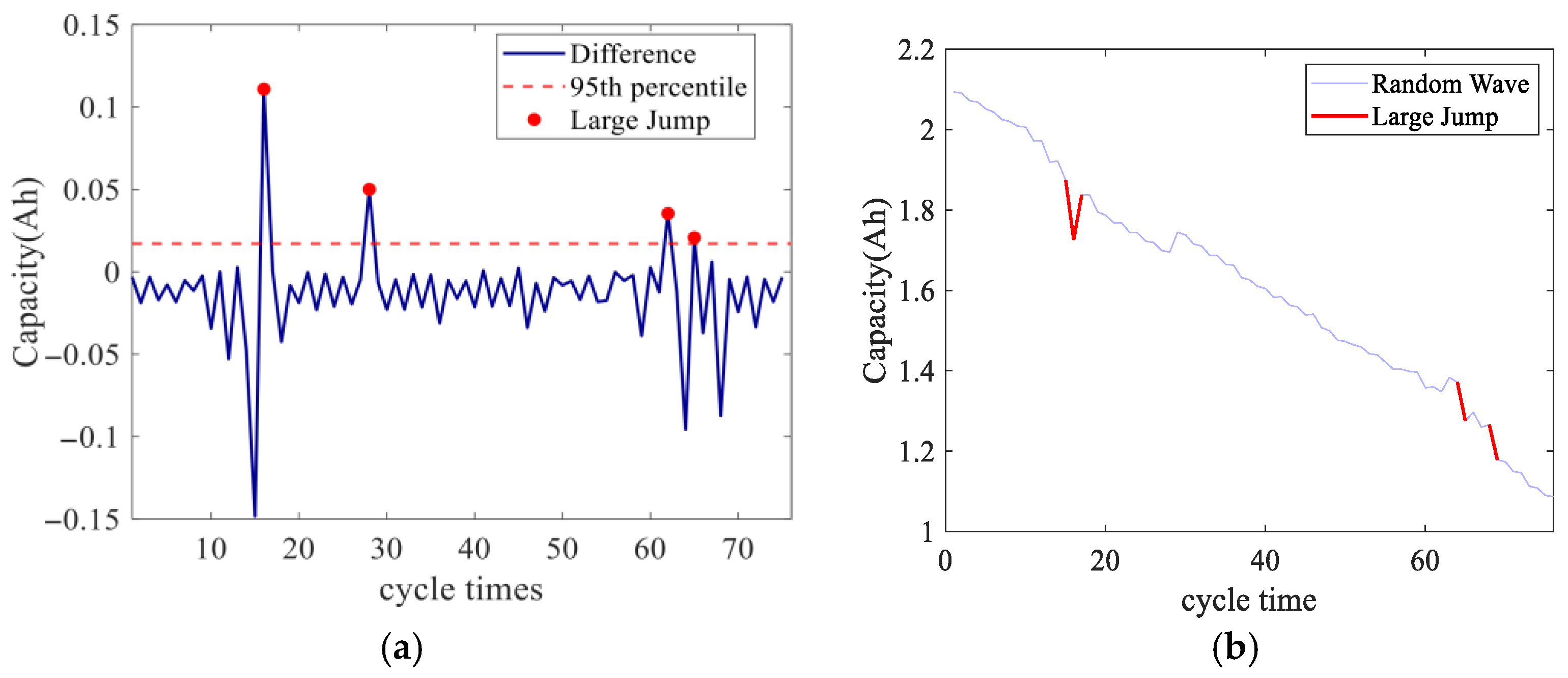
6. Case Study
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RUL | Remaining useful life |
| LRD | Long-range dependence |
| fPp | Fractional Poisson process |
| fBm | Fractional Brownian motion |
| fLsm | Fractional Lévy stable motion |
| EOL | End of life |
| Probability density motion | |
| LSTM | Long short-term memory |
| GPR | Gaussian process regression |
| RVM | Relevance vector machine |
| RNN | Recurrent neural network |
| SOH | State of health |
| Fractional Poisson process | |
| Fractional Brownian motion | |
| Hurst exponent | |
| Intensity of jumping | |
| Drift coefficient | |
| Diffusion parameter | |
| Exponent function | |
| 95 percentile |
References
- IEEE Std 1188-1996; IEEE Recommended Practice for Maintenance, Testing, and Replacement of Valve-regulated Leas-Acid(VRLA) Batteries for Aeationary Applications. IEEE: Piscataway, NJ, USA, 1996.
- Li, J.; Xiong, Z.; Wu, Y.; Li, H.; Liu, X.; Peng, H.; Zheng, Y.; Zhang, Q.; Liu, Q. Iron(Fe, Ni, Co)-based reansition metal compounds for lithium-sulfur batteries: Mechanism, progress and prospects. J. Energy Chem. 2022, 73, 513–532. [Google Scholar] [CrossRef]
- Cho, K.; Kim, S.; Kim, S.; Choi, J., II. Electrochemical Model-Based State-Space Approach for Real-Time Parameter Estimation of Lithium-Ion Batteries. In Proceedings of the Electro chemical Society Meeting Abstracts 244, Gothenburg, Sweden, 8–12 October 2023; The Electro chemical Society, Inc.: Pennington, NJ, USA, 2023; p. 3052. [Google Scholar]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- Liu, W.; Placke, T.; Chau, K.T. Overview of batteries and battery management for electric vehicles. Energy Rep. 2022, 8, 4058–4084. [Google Scholar] [CrossRef]
- Sui, X.; He, S.; Vilsen, S.B.; Meng, J.; Teodorescu, R.; Stroe, D.-I. A review of non-probabilistic machine learning-based state of health estimation techniques for Lithium-ion battery. Appl. Energy 2021, 300, 117346. [Google Scholar] [CrossRef]
- Severson, K.A.; Attia, P.M.; Jin, N.; Perkins, N.; Jiang, B.; Yang, Z.; Chen, M.H.; Aykol, M.; Herring, P.K.; Fraggedakis, D.; et al. Data-driven prediction of battery cycle life before capacity degradation. Nat. Energy 2019, 4, 383–391. [Google Scholar] [CrossRef]
- Chen, J.C.; Chen, T.L.; Liu, W.J.; Cheng, C.; Li, M.-G. Combining empirical mode decomposition and deep recurrent neural networks for predictive maintenance of lithium-ion battery. Adv. Eng. Inform. 2021, 50, 101405. [Google Scholar] [CrossRef]
- Li, X.; Yuan, C.; Wang, Z. Multi-time-scale framework for prognostic health condition of lithium battery using modified Gaussian process regression and nonlinear regression. J. Power Sources 2020, 467, 228358. [Google Scholar] [CrossRef]
- Jia, J.; Liang, J.; Shi, Y.; Wen, J.; Pang, X.; Zeng, J. SOH and RUL Prediction of Lithium-Ion Batteries Based on Gaussian Process Regression with Indirect Health Indicators. Energies 2020, 13, 375. [Google Scholar] [CrossRef]
- Peikun, S.; Zhenpo, W. Research of the Relationship between Li-ion Battery Charge Performance and SOH based on MIGA-Gpr Method. Energy Procedia 2016, 88, 608–613. [Google Scholar] [CrossRef]
- Xiao, Y.; Deng, S.; Han, F.; Wang, X.; Zhang, Z.; Peng, K. A Model-Data-Fusion Pole Piece Thickness Prediction Method With Multisensor Fusion for Lithium Battery Rolling Machine. IEEE Access 2022, 10, 55034–55050. [Google Scholar] [CrossRef]
- Feng, H.; Song, D. A health indicator extraction based on surface temperature for lithium-ion batteries remaining useful life prediction. J. Energy Storage 2021, 34, 102118. [Google Scholar] [CrossRef]
- Wang, R.; Feng, H. Remaining useful life prediction of lithium-ion battery using a novel health indicator. Qual. Reliab. Eng. Int. 2021, 37, 1232–1243. [Google Scholar] [CrossRef]
- Hu, C.; Youn, B.D.; Wang, P.; Yoon, J.T. Ensemble of data-driven prognostic algorithms for robust prediction of remaining useful life. Reliab. Eng. Syst. Saf. 2012, 103, 120–135. [Google Scholar] [CrossRef]
- Wang, X.T.; Wen, Z.X.; Zhang, S.Y. Fractional poisson process (ii). Chaos Solitons Fractals 2006, 28, 143–147. [Google Scholar] [CrossRef]
- Héctor, A.; Natalia, B.; Tania, R.; Soleded, T. Parameter estimation for a discrete time model driven by fractional Poisson process. Commun. Stat.-Theory Methods 2021, 52, 3452–3477. [Google Scholar]
- Saha, B.; Goebel, K. Battery Data Set, NASA AMES Prognostics Data Repository; NASA Ames Research Center: Moffett Field, CA, USA, 2007. [Google Scholar]


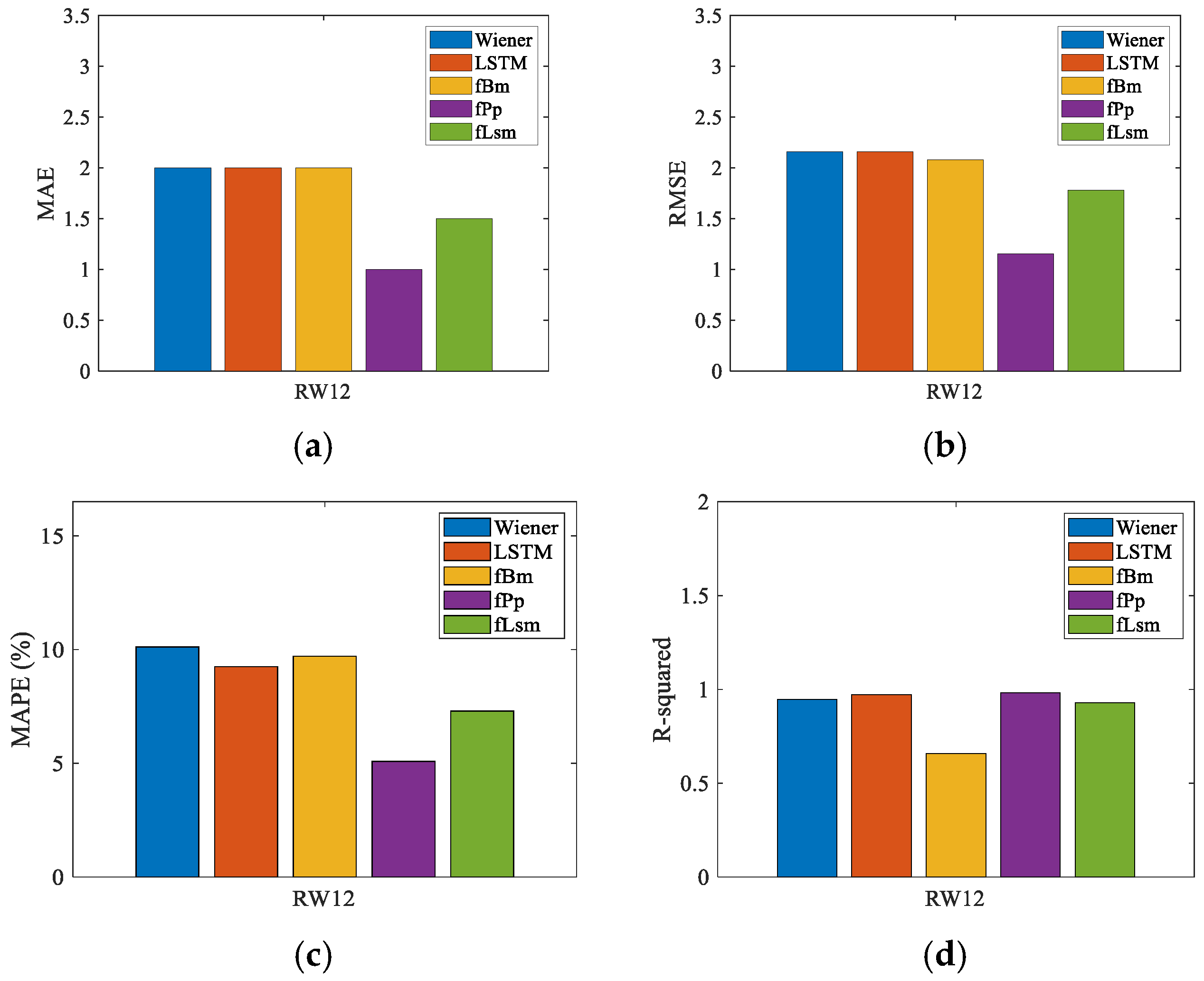
| Prediction Starting Point | 95 Percentile | ||||||
|---|---|---|---|---|---|---|---|
| 30 | 0.6257 | 0.0345 | 0.0531 | −0.0154 | 0.0385 | −2.2254 | 0.2007 |
| 32 | 0.6230 | 0.0645 | 0.0477 | −0.0145 | 0.0410 | −1.8797 | 0.0000 |
| 34 | 0.6167 | 0.0606 | 0.0430 | −0.0139 | 0.0420 | −1.8619 | 0.0342 |
| 36 | 0.6321 | 0.0571 | 0.0382 | −0.0134 | 0.0424 | −1.8504 | 0.0000 |
| 38 | 0.6446 | 0.0541 | 0.0335 | −0.0132 | 0.0418 | −1.8450 | 0.0067 |
| 40 | 0.6592 | 0.0513 | 0.0287 | −0.0129 | 0.0413 | −1.8413 | 0.0003 |
| Start Point | Actual RUL | Predicted RUL | AE | RE |
|---|---|---|---|---|
| 30 | 26 | 26 | 0 | 0.0000 |
| 32 | 24 | 23 | 1 | 0.0417 |
| 34 | 22 | 21 | 1 | 0.0455 |
| 36 | 20 | 18 | 2 | 0.1000 |
| 38 | 18 | 17 | 1 | 0.0556 |
| 40 | 16 | 15 | 1 | 0.0625 |
| Battery | Model | MAE | MAPE (%) | RMSE | |
|---|---|---|---|---|---|
| RW12 | fPp | 1.0000 | 5.0863 | 1.1547 | 0.9823 |
| fBm | 2.0000 | 9.7122 | 2.0817 | 0.6577 | |
| LSTM | 2.0000 | 9.2484 | 2.1602 | 0.9725 | |
| fLsm | 1.5000 | 7.2959 | 1.7795 | 0.9292 | |
| Wiener | 2.0000 | 10.1128 | 2.1602 | 0.9468 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Liu, F.; Kudreyko, A.; Wu, Z.; Song, W. Fractional Poisson Process for Estimation of Capacity Degradation in Li-Ion Batteries by Walk Sequences. Fractal Fract. 2025, 9, 558. https://doi.org/10.3390/fractalfract9090558
Shi J, Liu F, Kudreyko A, Wu Z, Song W. Fractional Poisson Process for Estimation of Capacity Degradation in Li-Ion Batteries by Walk Sequences. Fractal and Fractional. 2025; 9(9):558. https://doi.org/10.3390/fractalfract9090558
Chicago/Turabian StyleShi, Jing, Feng Liu, Aleksey Kudreyko, Zhengyang Wu, and Wanqing Song. 2025. "Fractional Poisson Process for Estimation of Capacity Degradation in Li-Ion Batteries by Walk Sequences" Fractal and Fractional 9, no. 9: 558. https://doi.org/10.3390/fractalfract9090558
APA StyleShi, J., Liu, F., Kudreyko, A., Wu, Z., & Song, W. (2025). Fractional Poisson Process for Estimation of Capacity Degradation in Li-Ion Batteries by Walk Sequences. Fractal and Fractional, 9(9), 558. https://doi.org/10.3390/fractalfract9090558








