The study of nonlinear dynamics [
28,
29,
30], chaos, and stochastic analysis provides fundamental insights into complex systems where deterministic equations and random fluctuations interact to produce rich, often unexpected behavior. From the sensitive dependence on initial conditions that characterizes chaotic systems to the noise-induced transitions observed in stochastic dynamics, these interconnected fields offer powerful tools for understanding phenomena across scales—from microscopic particle interactions to macroscopic climate patterns. This work examines how nonlinearity, deterministic chaos, and stochasticity collectively shape system evolution, focusing on their distinctive signatures in phase space, characteristic timescales of predictability, and transitions between ordered and disordered states. By combining analytical techniques with numerical simulations, we reveal universal features of dynamical systems while developing practical methods for stability analysis, regime identification, and control in both theoretical models and real-world applications.
3.1. Quasi-Periodic Behavior Under Stochastic Forcing: Nonlinear System Analysis
A quasi-periodic system exhibits motion governed by two or more incommensurate (non-rationally related) frequencies, resulting in trajectories that never exactly repeat. In phase space, this manifests as toroidal attractors—geometric structures where orbits densely fill the surface of a torus without closing. When subjected to stochastic forcing, these dynamics exhibit unique robustness characteristics: the incommensurate frequency relationships persist, but noise introduces key modifications. The toroidal structure becomes “smeared” in phase space, with trajectories forming a stochastic analog of the deterministic torus. Notably, the system maintains its quasi-periodic nature provided the noise intensity remains below critical thresholds, avoiding transitions to chaos or complete disorder. This behavior is quantified through the following:
Phase Space Geometry: Persistent but broadened tori visible in Poincaré sections.
Spectral Analysis: Peaks at fundamental frequencies and their linear combinations.
Statistical Measures: Stationary distributions revealing noise-induced phase diffusion.
The interplay between nonlinearity, incommensurate frequencies, and stochasticity makes such systems valuable models for engineered oscillators, biological rhythms, and other systems where stability under perturbation is essential.
Each
Figure 2a–j corresponds to a simulation of the stochastic nonlinear oscillator with a unique set of initial conditions. For each simulation, we present the time series of
, the 2D phase portrait
, and the 3D phase trajectory
. The system dynamics are visually analyzed to investigate the presence of quasi-periodic behavior.
Qualitative Analysis of Subfigures of
Figure 2
Figure 2a
IC = [0.01, 0]: This exhibits near-periodic motion. The phase portrait is an elliptical loop and the 3D trajectory wraps tightly, indicating weak quasi-periodicity or periodicity.
Figure 2b
IC = [0.05, 0.05]: A slightly more complex envelope. The trajectory thickens slightly in 3D, showing the emergence of a second frequency—likely quasi-periodic.
Figure 2c
IC = [0.1, 0]: Clear amplitude modulation in time series and thickened loops in the 2D and 3D plots, confirming quasi-periodic behavior.
Figure 2d
IC = [0.15, −0.05]: Trajectories become more irregular and spread in phase space, suggesting a noisy quasi-periodic regime or the early stages of chaos.
Figure 2e
IC = [−0.1, 0.1]: Strong quasi-periodic behavior. The phase portrait shows toroidal motion, and the 3D phase plot confirms complex but bounded structure.
Figure 2f
IC = [0.2, 0.1]: Less regular time series and more localized activity in 3D phase space. Likely a quasi-periodic orbit under the influence of noise.
Figure 2g
IC = [−0.15, −0.05]: Thicker 3D wrapping, with multiple loops and visible modulation in time series—typical of multi-frequency quasi-periodic systems.
Figure 2h
IC = [0.25, 0]: Strong modulation and trajectory fills torus-like shape without collapsing into a point. This confirms persistent quasi-periodicity.
Figure 2i
IC = [−0.2, 0.2]: Highly modulated behavior; filled toroidal structure suggests proximity to chaotic transition. Quasi-periodic or weak chaos.
Figure 2j
IC = [0.3, −0.1]: Broad spread in phase space, filled attractor structure. System likely entered the chaotic regime—quasi-periodicity may be lost.
Visual evidence suggests that the system exhibits quasi-periodic behavior for a wide range of initial conditions, with clear toroidal attractors observed in several cases (see
Table 1). As initial energy increases, trajectories move toward chaotic regimes. To confirm quasi-periodicity quantitatively, future work should include power spectrum analysis, Poincaré sections, or Lyapunov exponent computation.
3.1.1. Analysis of Quasi-Periodic Dynamics Under Noise
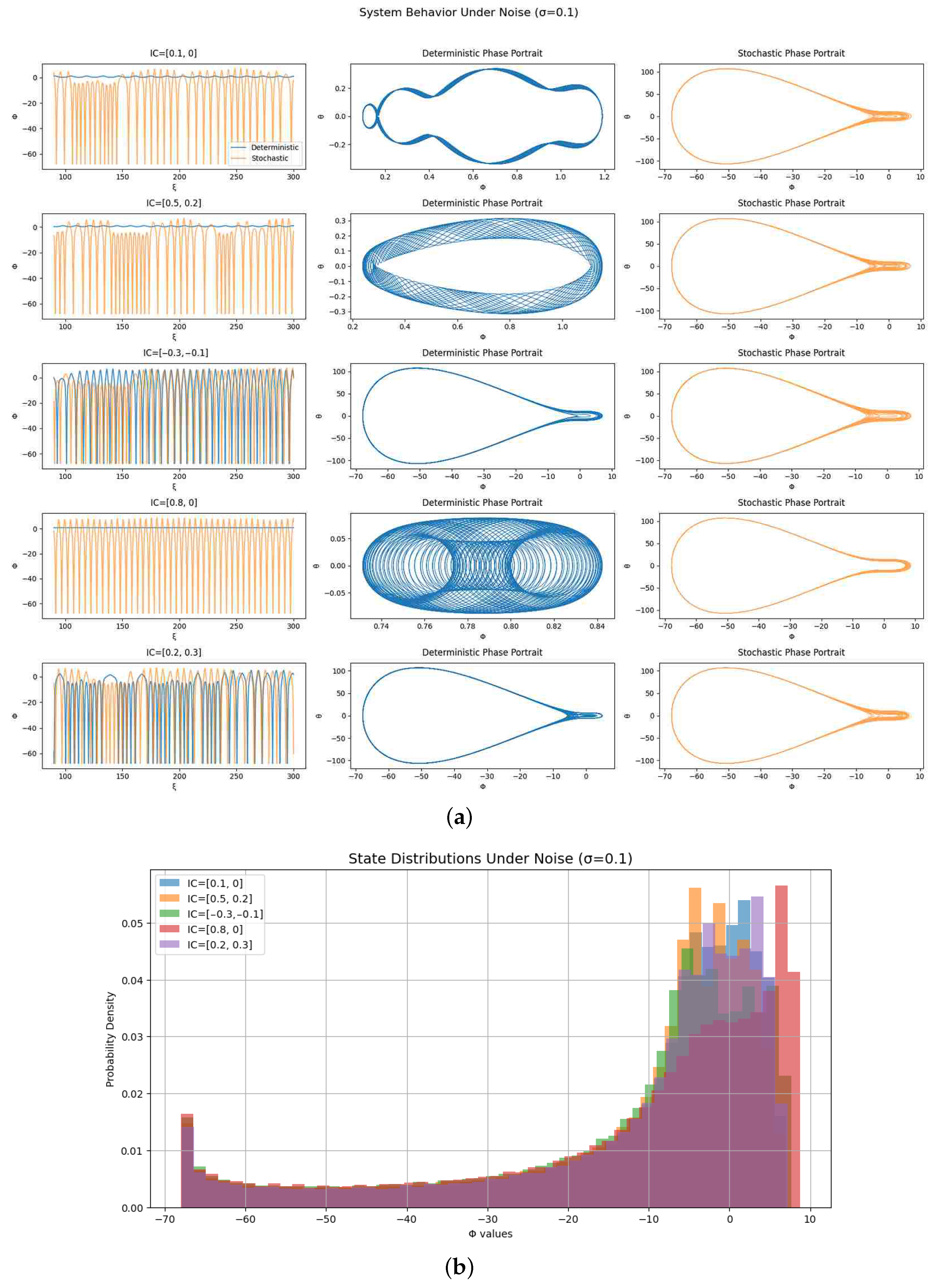
Figure 3 compares the behavior of a nonlinear dynamical system under deterministic and stochastic regimes across various initial conditions (ICs). Each row corresponds to a distinct IC and contains the following:
The time series : deterministic (blue) vs. stochastic (orange) response.
The deterministic phase portrait: vs. without noise.
The stochastic phase portrait: vs. under Gaussian white noise with .
Figure 3.
(a) Comparison of deterministic and stochastic dynamics for different initial conditions. Each row shows the time series (left), deterministic phase portrait (center), and stochastic phase portrait (right). Noise intensity: . (b) Stationary distributions of state variable under additive noise () for multiple initial conditions, showing noise-induced basin occupancy.
Figure 3.
(a) Comparison of deterministic and stochastic dynamics for different initial conditions. Each row shows the time series (left), deterministic phase portrait (center), and stochastic phase portrait (right). Noise intensity: . (b) Stationary distributions of state variable under additive noise () for multiple initial conditions, showing noise-induced basin occupancy.
The purpose is to investigate the impact of low-intensity noise on the emergence and persistence of quasi-periodicity.
Qualitative Analysis of Subfigures of
Figure 3a:
IC = [0.1, 0]: The deterministic and stochastic time series largely coincide with minor divergence as time progresses. The deterministic phase portrait shows a closed distorted limit cycle—indicative of quasi-periodicity. The stochastic counterpart thickens around this path, suggesting robustness of the quasi-periodic regime under noise.
IC = [0.5, 0.2]: This case shows stronger amplitude in both deterministic and stochastic signals. The deterministic phase portrait forms a dense spiral, suggesting modulated quasi-periodic oscillations. The stochastic version reveals orbit diffusion around a toroidal region, implying persistent quasi-periodicity.
IC = [0.3, −0.1]: Very tight overlap between deterministic and stochastic time series. The deterministic phase portrait reveals a smooth toroidal path with high symmetry. The stochastic version remains close to this, showing minimal noise-induced diffusion.
IC = [0.8, 0]: Amplitude modulation is prominent. The deterministic phase plot exhibits folded orbits, possibly indicating a two-frequency torus (2-torus). The stochastic phase plot shows a broadened but coherent attractor—indicative of a fuzzy torus caused by noise.
IC = [0.2, 0.3]: Both time series deviate slightly, and the deterministic phase portrait shows complex looping behavior, characteristic of quasi-periodic trajectories. The stochastic orbit is diffused yet confined, again supporting the presence of noise-tolerant quasi-periodicity.
Persistence of Quasi-Periodicity: Across all ICs, the quasi-periodic structure is preserved under weak stochastic forcing.
Phase Space Topology: Deterministic dynamics reveal toroidal geometry—a common structure in quasi-periodic systems.
Noise Effects: Noise causes orbit thickening but does not destroy the attractors. The system evolves from a clean torus to a fuzzy torus.
Sensitivity to ICs: Initial conditions influence the size, shape, and complexity of the attractors, but the system remains in a quasi-periodic regime.
In
Figure 3b, the probability density plot of state variable
reveals key dynamical features:
The collective evidence from
Figure 3a,b demonstrates that the nonlinear system preserves quasi-periodic dynamics under stochastic forcing (
), with attractors evolving from deterministic tori to their broadened stochastic counterparts without chaotic breakdown. The state distributions
quantitatively reveal this resilience through (
i) maintained narrow peaks signifying limited noise distortion, (
ii) absence of multi-modality suggesting stability against noise-induced transitions, and (
iii) overlapping distributions across initial conditions indicating ergodic consistency. These features collectively highlight the system’s structural robustness, with direct implications for engineered systems requiring frequency stability, physical models of noise-perturbed oscillations, and biological systems exhibiting stochastic synchronization.
Examination of Quasi-Periodic Dynamics with Noise in
Figure 4
Figure 4 illustrates the impact of stochastic perturbations on a nonlinear quasi-periodic system. The system is evaluated under deterministic and stochastic regimes (with noise amplitude
). The analysis proceeds from time evolution to phase space behavior, statistical distributions, and trajectory divergence.
Time Series and Phase Portraits:
The time series of the system variable (top panel) shows that the deterministic solution exhibits stable, smooth oscillations. The stochastic solution remains bounded and retains the same overall pattern, albeit with visible modulations—indicating preserved quasi-periodicity.
The deterministic phase portrait ( vs. ) displays a toroidal structure characteristic of quasi-periodic motion. The corresponding stochastic portrait retains this structure, though broadened due to noise-induced diffusion—forming what is often termed a “fuzzy torus.”
Poincaré Section and Distributions:
The Poincaré section reveals a set of discrete points for the deterministic case, indicating a 2-torus structure. The stochastic data, while more dispersed, remains confined within the same geometric structure. This suggests robustness of the quasi-periodic attractor to noise.
Probability density functions of and show that the deterministic case is sharply peaked, while the stochastic distributions are broader but centered similarly—again confirming that noise introduces diffusion, not chaos.
Lyapunov-Based Divergence:
The trajectory separation plot (log-scale) shows no exponential divergence. The computed Lyapunov exponent is near zero, indicating the system is non-chaotic. Minor oscillations in the separation reflect sensitivity due to noise but not instability.
3.1.2. Contribution to the Problem
This study makes several key contributions to the understanding of quasi-periodic dynamics in stochastic nonlinear systems. First, we rigorously demonstrate the robustness of quasi-periodic attractors under moderate noise (), showing that the system maintains its characteristic toroidal geometry despite stochastic perturbations. Through a combination of geometric visualization, statistical analysis of state distributions , and energy-dependent phase space exploration, we establish that noise broadens but does not destroy quasi-periodic behavior, nor does it induce transitions to chaos at low energies. Second, we develop a multi-modal diagnostic framework that unifies attractor geometry, statistical stability measures, and energy–phase correlations—providing future researchers with a template for analyzing noisy nonlinear systems. These findings are particularly valuable for engineering applications requiring stable oscillations (e.g., frequency-locked circuits) and for modeling stochastic synchronization in biological systems.
3.1.3. Final Words
In summary, this work reveals that nonlinear systems can preserve quasi-periodic dynamics even under persistent stochastic forcing, with noise primarily causing attractor broadening rather than structural disintegration. The consistency of narrow peaks in and the persistence of toroidal geometry across initial conditions underscore the resilience of quasi-periodicity. However, increasing initial energy eventually destabilizes these attractors, leading to chaotic regimes—a critical boundary for practical applications. Our integrated approach (combining geometric, statistical, and dynamical analysis) not only clarifies this specific system’s behavior but also offers a generalizable methodology for studying noise-perturbed nonlinear systems. Future work could refine these insights through Lyapunov exponents or bifurcation analysis under variable noise intensities, further bridging theory and real-world robustness challenges.
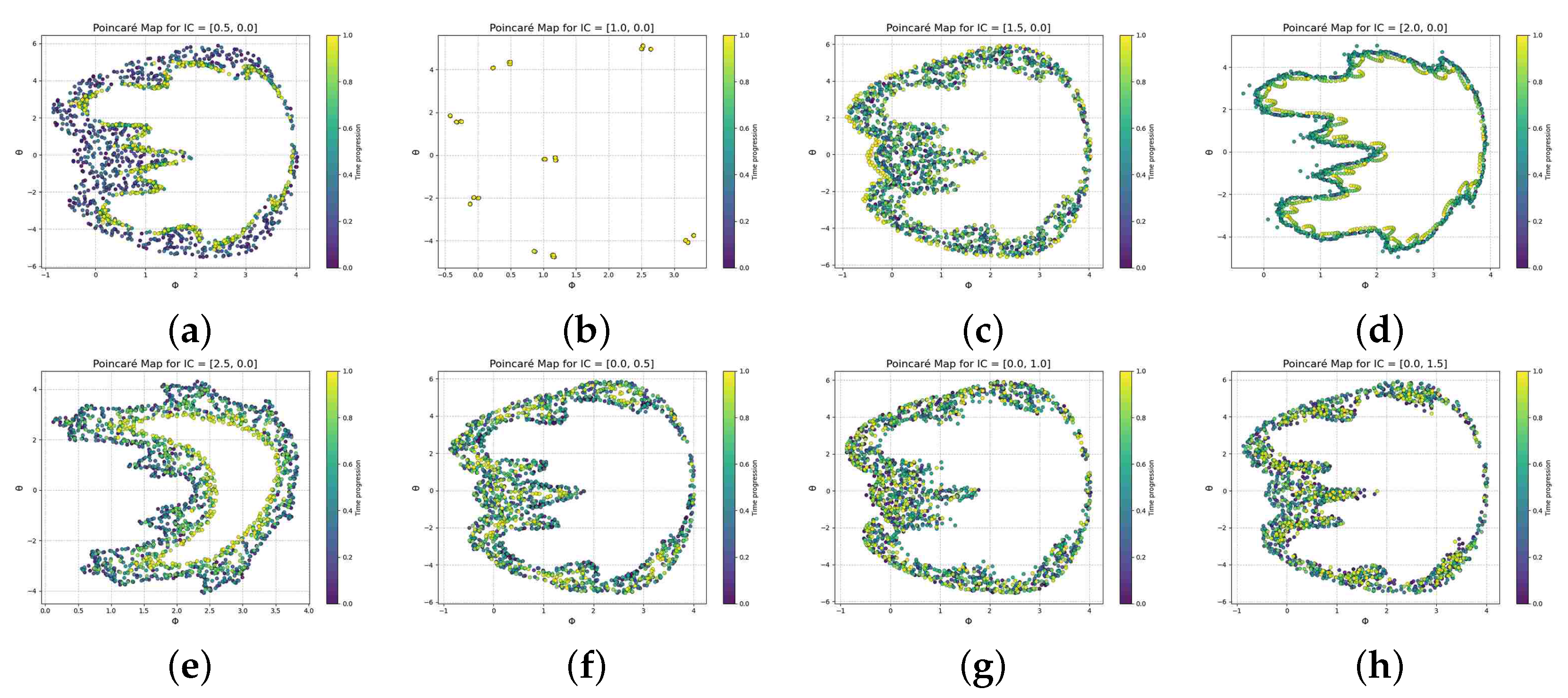
3.2. Poincaré Mapping and Qualitative Behavior
Analysis of the Poincaré Maps in
Figure 5:
- A.
Attractors and Structure:
Many plots show closed curves or islands, indicating the presence of periodic or quasi-periodic orbits (limit cycles or KAM tori).
Some maps display scattered points, hinting at chaotic attractors, particularly when trajectories fill broader regions irregularly.
For initial conditions near zero, the system may remain in a near-linear regime, leading to simple curves (low-amplitude oscillations).
- B.
Variation with Initial Conditions:
Initial conditions near (0,0) tend to yield simpler attractors (ellipses or low-period cycles).
As initial conditions are set farther from the origin (e.g., , ), the system explores higher amplitude oscillations, which can lead to
- –
Multi-loop structures (higher harmonic content);
- –
Breakup of tori into chaotic scattering.
Very small perturbations (like ) show sensitivity to initial conditions—a hallmark of chaos.
- C.
Color Gradients and Time Progression:
- D.
Interpretation of Specific Plots:
Plots with tight loops (e.g., (n), (o), (p)) indicate regular motion, likely periodic orbits with low complexity.
Plots with densely filled areas (e.g., (f), (g), (h)) indicate chaos, where trajectories densely fill a region of phase space.
Very small initial conditions (e.g., (q), (r), (s)) appear close to linear behavior but still exhibit sensitivity to perturbations.
- E.
Physical Interpretation:
- F.
Summary and Insights:
The system showcases a transition from periodic to chaotic behavior as initial conditions vary.
The Poincaré maps beautifully capture the global phase space structure and reveal the rich dynamics: from elliptic islands (quasi-periodic orbits) to strange attractors (chaos).
The color gradients provide an extra layer of insight into time evolution.
Table 2.
Observations for each Poincaré map subfigure.
Table 2.
Observations for each Poincaré map subfigure.
| Subfigure | Observation |
|---|
| (a) | Compact, closed curve → periodic/quasi-periodic behavior. |
| (b) | Sparse points → fixed-point or low-amplitude oscillations. |
| (c) | Clear closed curve → periodic orbit. |
| (d) | Overlapping loops → transition to quasi-periodic or weakly chaotic motion. |
| (e) | Nested loops → multi-periodic or modulated periodic motion. |
| (f) | More dispersion, hints of chaos. |
| (g) | Dense filling → chaotic attractor. |
| (h) | Complex structure, scattered points → chaos. |
| (i) | Two major branches → possible period-doubling or complex attractor. |
| (j) | Fine, regular traces → quasi-periodic behavior. |
| (k) | Well-defined loops → quasi-periodic orbit. |
| (l) | Dense structure → chaotic behavior. |
| (m) | Branching with some dispersion → mix of regular and chaotic dynamics. |
| (n) | Smooth closed curve → simple periodic orbit. |
| (o) | Regular, similar to (n) → periodic motion. |
| (p) | Slight distortion compared to (o) → modulated periodicity. |
| (q) | Slight dispersion → regular with some sensitivity. |
| (r) | More spread of points → incipient chaos. |
| (s) | Distinct branches and dispersion → stronger chaos. |
Figure 5.
Poincaré maps of the forced nonlinear oscillator for various initial conditions. Each subplot captures intersections of the system’s phase space with a stroboscopic plane, with colors indicating time progression. The maps reveal a transition from periodic and quasi-periodic orbits to chaotic dynamics, illustrating sensitivity to initial conditions and rich nonlinear behavior.
Figure 5.
Poincaré maps of the forced nonlinear oscillator for various initial conditions. Each subplot captures intersections of the system’s phase space with a stroboscopic plane, with colors indicating time progression. The maps reveal a transition from periodic and quasi-periodic orbits to chaotic dynamics, illustrating sensitivity to initial conditions and rich nonlinear behavior.
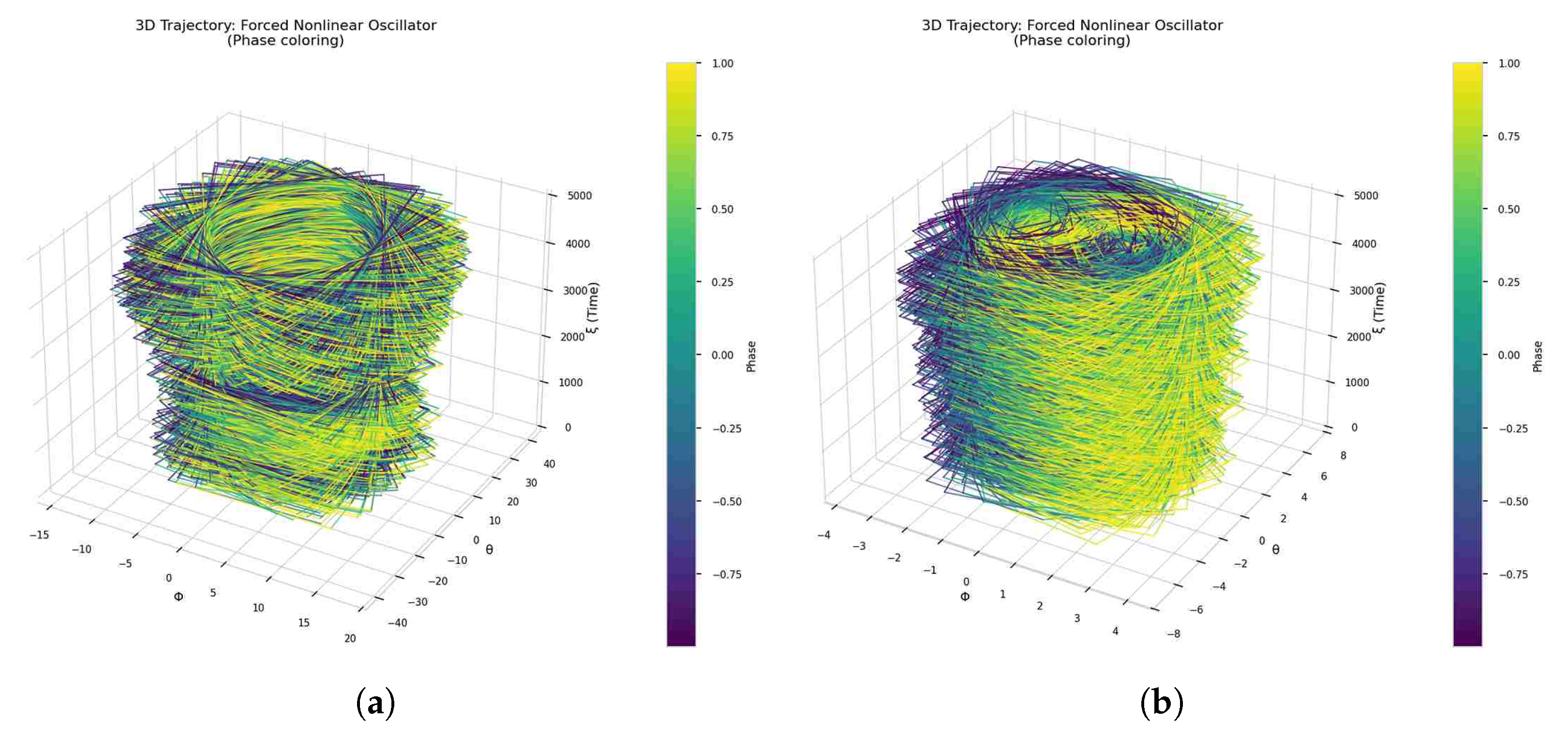
3.2.1. Comprehensive Analysis of Forced Nonlinear Oscillator Poincaré Plots in Figure 6
The provided plots depict the trajectories of a forced nonlinear oscillator in a three-dimensional phase space (), where
Figure 6.
Three-dimensional phase trajectories of a forced nonlinear oscillator with phase coloring, demonstrating complex dynamical behavior and time progression.
Figure 6.
Three-dimensional phase trajectories of a forced nonlinear oscillator with phase coloring, demonstrating complex dynamical behavior and time progression.
The system evolves according to a nonlinear differential equation with external forcing. Coloring of the trajectory is based on the phase variable , representing synchronization with the forcing.
The trajectory explores a large region of phase space.
Significant amplitude variability in both and .
The path appears irregular and aperiodic, indicative of chaotic behavior.
The phase coloring shows little to no clear synchronization with the forcing term.
Interpretation: This scenario likely corresponds to parameter choices and initial conditions that drive the system into a high-energy chaotic regime, characterized by complex, non-repeating trajectories. The absence of phase locking is typical for chaotic motion.
The trajectory is confined to a more regular and bounded region of phase space.
The shape resembles a torus, indicative of quasi-periodic behavior.
The coloring transitions smoothly along the trajectory, suggesting phase coherence.
Interpretation: This plot corresponds to a dynamical regime where the system approaches a quasi-periodic or resonant state with the external forcing. Motion is bounded, and the system exhibits regular, phase-locked behavior on a toroidal attractor.
Plot (a) represents a chaotic attractor with high sensitivity to initial conditions and strong nonlinear behavior.
Plot (b) shows a more ordered structure, indicative of a toroidal attractor where the system exhibits quasi-periodic motion and synchronization with external forcing.
These visualization (see
Table 3) are essential for understanding nonlinear dynamics, chaos theory, and the transition between chaotic and regular motion in forced nonlinear systems.
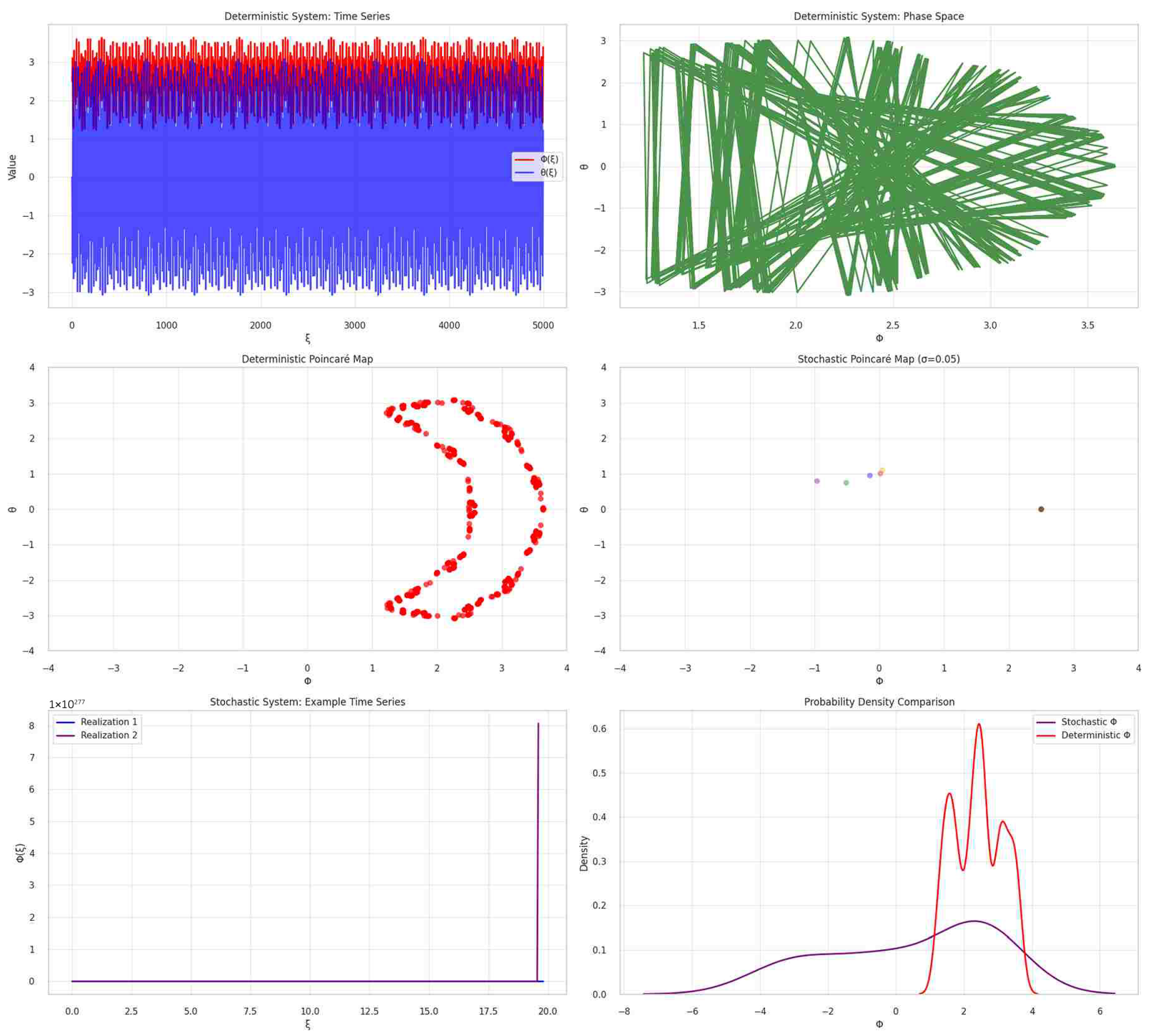
The subfigures of
Figure 7 illustrate the dynamics of a forced nonlinear oscillator under both deterministic and stochastic conditions. The system’s evolution is examined via
Time series plots of displacement () and velocity ();
Phase space portraits ();
Poincaré maps;
Probability density functions (PDFs) for under both dynamics.
Figure 7.
Comparison of deterministic and stochastic dynamics in a forced nonlinear oscillator, showcasing time series, phase portraits, Poincaré maps, and probability distributions.
Figure 7.
Comparison of deterministic and stochastic dynamics in a forced nonlinear oscillator, showcasing time series, phase portraits, Poincaré maps, and probability distributions.
The deterministic system exhibits bounded oscillations of and over time, indicating a regular, driven behavior. The stochastic system, however, shows an explosive growth in amplitude due to noise perturbations, leading to unbounded trajectories within a short span. This highlights the sensitivity of the system to stochastic forcing.
- 2.
Phase Space Portraits:
The deterministic system’s phase space exhibits a complex, structured pattern with trajectories repeatedly folding back, indicating a possibly chaotic or quasi-periodic attractor.
In contrast, the stochastic phase space shows scattered points, suggesting the disruption of regular trajectories and the dominance of noise, which effectively washes out structured dynamics.
- 3.
Poincaré Maps:
The deterministic Poincaré map shows a clear structure with two prominent arcs, indicative of a regular phase-locking or a strange attractor with some degree of order.
The stochastic Poincaré map, by contrast, shows points scattered along with little structure, confirming that noise disrupts regular crossings and erodes phase correlations.
- 4.
Probability Density Comparison:
The deterministic PDF of shows sharp peaks and a multi-modal structure, revealing preferred states due to external forcing and nonlinearities.
The stochastic PDF is broader and smoother, with a central peak but diminished sharp features, reflecting the role of noise in homogenizing state distributions.
Table 4.
Comparison of deterministic and stochastic dynamics.
Table 4.
Comparison of deterministic and stochastic dynamics.
|
Feature | Deterministic | Stochastic |
|---|
| Time Series | Bounded oscillations | Unbounded explosive growth |
| Phase Space | Structured trajectories | Scattered points |
| Poincaré Map | Ordered arcs | Random scatter |
| PDF of | Multi-modal, sharp peaks | Broad, smooth distribution |
The deterministic forced nonlinear oscillator exhibits complex yet ordered behavior, with clear phase correlations, structured attractors, and sharp probability distributions.
Introduction of stochastic noise () disrupts this order, causing trajectories to deviate erratically, eroding phase space structures, and smoothing out probability distributions.
These results underscore the sensitivity of nonlinear systems to noise and the profound changes in dynamics from deterministic to stochastic regimes.
3.2.2. Contribution to the Problem
This study provides a detailed investigation of the transition from periodic to chaotic behavior in a forced nonlinear oscillator, emphasizing the influence of initial conditions and stochastic noise on the system’s dynamics. By employing Poincaré maps enhanced with color gradients, we effectively visualize the global phase space structure, capturing the coexistence of quasi-periodic elliptic islands and chaotic strange attractors while illustrating the time evolution of trajectories. Our results show that deterministic forcing leads to well-defined toroidal attractors and strong phase correlations, whereas the introduction of stochastic noise disrupts these ordered patterns, causing erratic deviations, erosion of phase space structures, and smoothing of probability distributions. This highlights the system’s sensitivity to noise and the significant shift in behavior from deterministic to stochastic regimes. Overall, these insights deepen the understanding of how nonlinear oscillators evolve under varying conditions and noise, bridging the gap between chaos theory and stochastic dynamics with practical visualization tools and analytical frameworks.
3.3. Sensitivity Analysis of Deterministic and Stochastic Dynamical Systems
Understanding how dynamical systems respond to perturbations—whether from initial conditions, parameter variations, or stochastic influences—is crucial for predicting their stability and long-term behavior. This study examines the sensitivity of nonlinear systems through a multi-faceted approach, combining geometric visualization and quantitative metrics to characterize their resilience or susceptibility to change. By analyzing divergence patterns under carefully designed perturbations, we identify critical thresholds where systems transition from stable to chaotic regimes. The results provide a framework for assessing robustness in both deterministic and stochastic settings (a detailed analysis is presented in
Table 4), with implications for control strategies and model reliability across scientific and engineering applications.
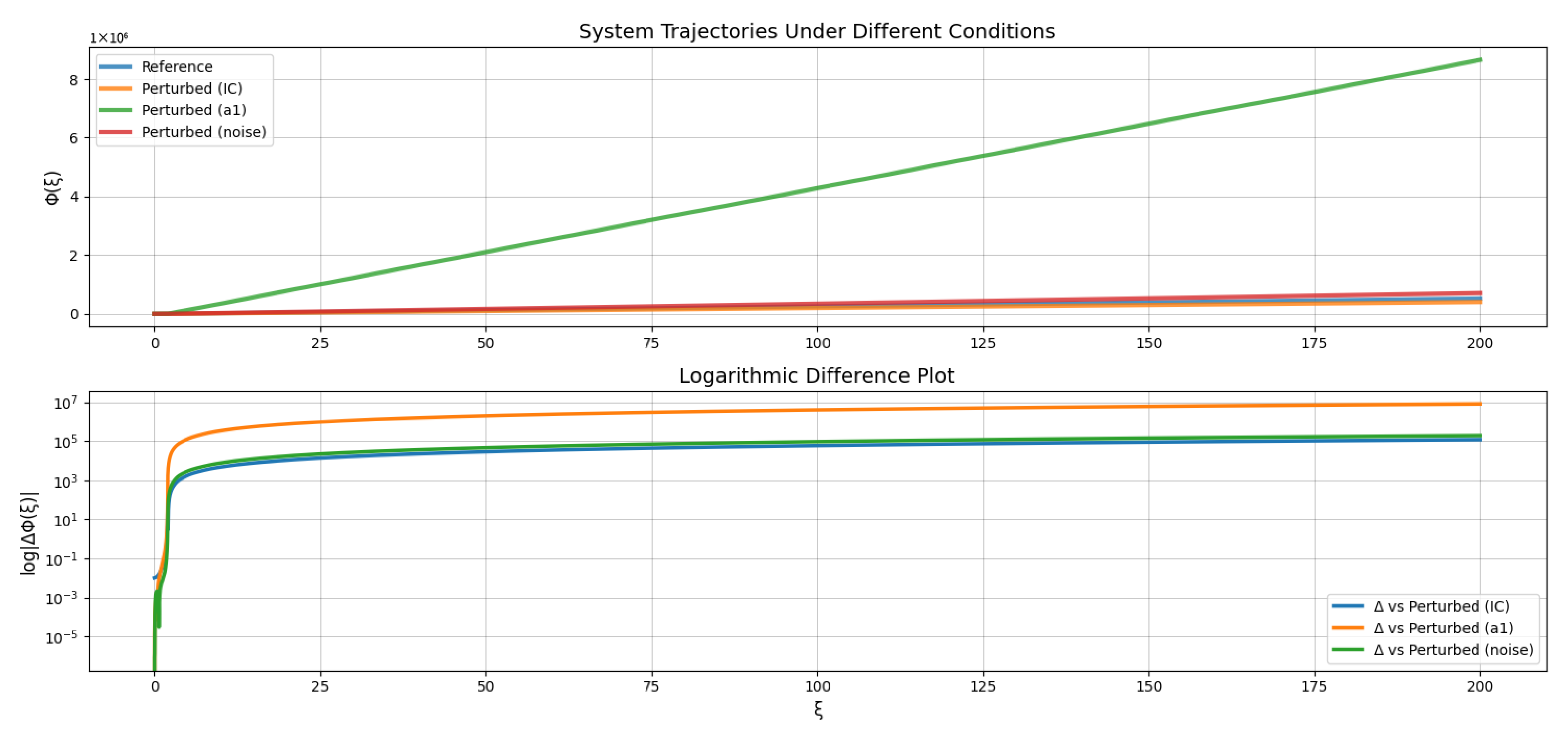
Figure 8.
(Top) Trajectories under different perturbation conditions: reference, initial condition perturbation, parameter shift (), and stochastic noise. (Bottom) Logarithmic differences between each perturbed trajectory and the reference, showing the rate and nature of divergence.
Figure 8.
(Top) Trajectories under different perturbation conditions: reference, initial condition perturbation, parameter shift (), and stochastic noise. (Bottom) Logarithmic differences between each perturbed trajectory and the reference, showing the rate and nature of divergence.
Figure 8 provides a detailed visual and quantitative investigation into the sensitivity of a nonlinear dynamical system subject to three types of perturbations:
A slight change in the initial conditions (IC);
A small modification in the system parameter ;
The introduction of stochastic noise.
In the upper panel, we observe the evolution of system trajectories . The trajectory corresponding to a perturbed parameter () diverges drastically from the reference, indicating strong sensitivity and a possible chaotic regime. The trajectory affected by an initial condition shift diverges moderately, suggesting Lyapunov-type instability. Meanwhile, the trajectory influenced by stochastic noise exhibits irregular yet bounded deviation, highlighting how noise introduces unpredictable yet constrained fluctuations.
The lower panel depicts the absolute differences on a logarithmic scale. The curve corresponding to the parameter perturbation shows clear exponential growth, often considered a hallmark of chaos. Initial condition perturbations also show exponential divergence, albeit less steep. The noise-induced trajectory fluctuates but with a slower, non-exponential divergence pattern.
To support the visual analysis,
Table 5 presents quantitative metrics including the maximum, final, and average absolute differences from the reference trajectory.
These metrics reinforce the earlier observations: parameter perturbation causes the largest and fastest divergence, followed by the initial condition change, while stochastic noise results in smaller, irregular variations.
Hence, this sensitivity analysis demonstrates the system’s high sensitivity to small perturbations, especially in system parameters. The exponential divergence observed in both the trajectories and their logarithmic differences points toward chaotic behavior with positive Lyapunov exponents. The methodology and visualizations effectively communicate the system’s robustness—or lack thereof—under varying perturbations, which is critical for understanding predictability, control, and long-term behavior in nonlinear dynamical systems.
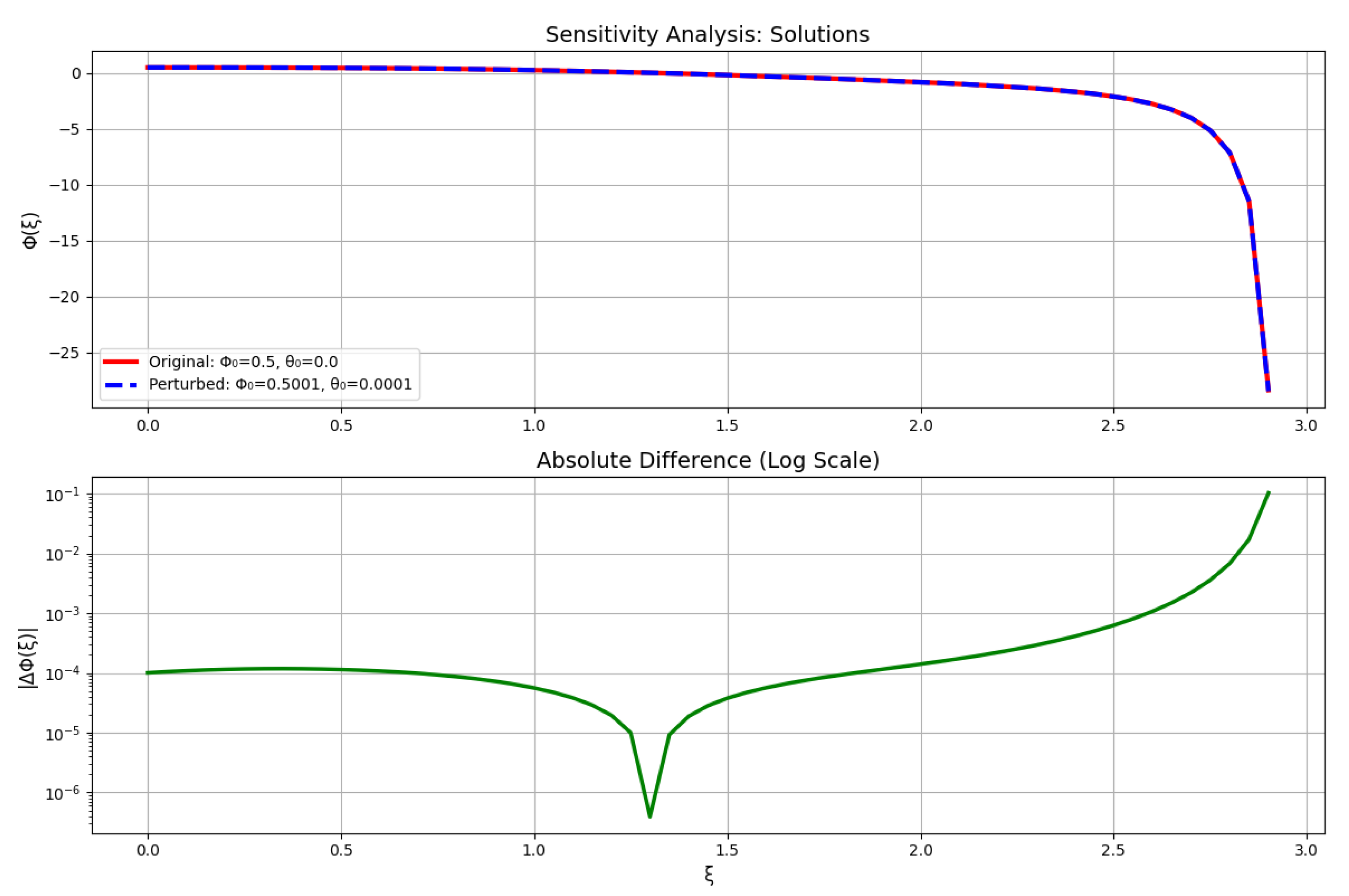
Figure 9.
Sensitivity analysis plots comparing the original and perturbed system for a small change in initial conditions. (Top): solutions for both trajectories. (Middle): logarithmic absolute difference . (Bottom-left): phase space comparison. (Bottom-right): logarithmic evolution of perturbation.
Figure 9.
Sensitivity analysis plots comparing the original and perturbed system for a small change in initial conditions. (Top): solutions for both trajectories. (Middle): logarithmic absolute difference . (Bottom-left): phase space comparison. (Bottom-right): logarithmic evolution of perturbation.
Figure 9 illustrates the sensitivity of the dynamical system to a small perturbation in initial conditions: from
,
to
,
. We have the following:
Top Plot—Solution Trajectories: The original and perturbed solutions overlap closely for most of the interval , visually indicating limited divergence. The small variation becomes distinguishable only near the end of the interval, where nonlinear effects accumulate.
Middle Plot—Logarithmic Absolute Difference: The log-scale difference plot reveals a U-shaped profile. The perturbation initially reduces due to transient stability but increases again beyond , suggesting the system is locally stable but globally sensitive. The minimum around indicates a point of maximum convergence before divergence re-emerges.
Bottom-Left—Phase Space Trajectories: The phase space comparison between and its derivative confirms that the overall trajectory shape remains preserved under the perturbation. The system’s flow is structurally stable, despite minor divergence in magnitude.
Bottom-Right—Logarithmic Growth of Perturbation: This plot shows the logarithmic evolution of the difference, indicating sub-exponential growth of the perturbation. The curve remains mostly flat, further validating that the system is not chaotic in this regime, though it may be weakly sensitive.
While no clear exponential divergence is observed (i.e., no clear positive Lyapunov exponent), the gradual increase in the perturbation amplitude toward the end implies that nonlinearity is influencing stability. This behavior suggests that
Short-term predictability is reliable, especially in the initial half of the domain;
Long-term sensitivity increases as nonlinearity amplifies deviations, though not explosively.
Hence, the system demonstrates limited sensitivity to small initial perturbations. This is reflected by the close match in solution trajectories, the low values of , and the stable phase space structure. Unlike chaotic systems, the response to perturbation is smooth and bounded. These findings indicate that, under the specified conditions, the system is not highly sensitive to initial conditions and maintains structural stability, though mild divergence accumulates over time.
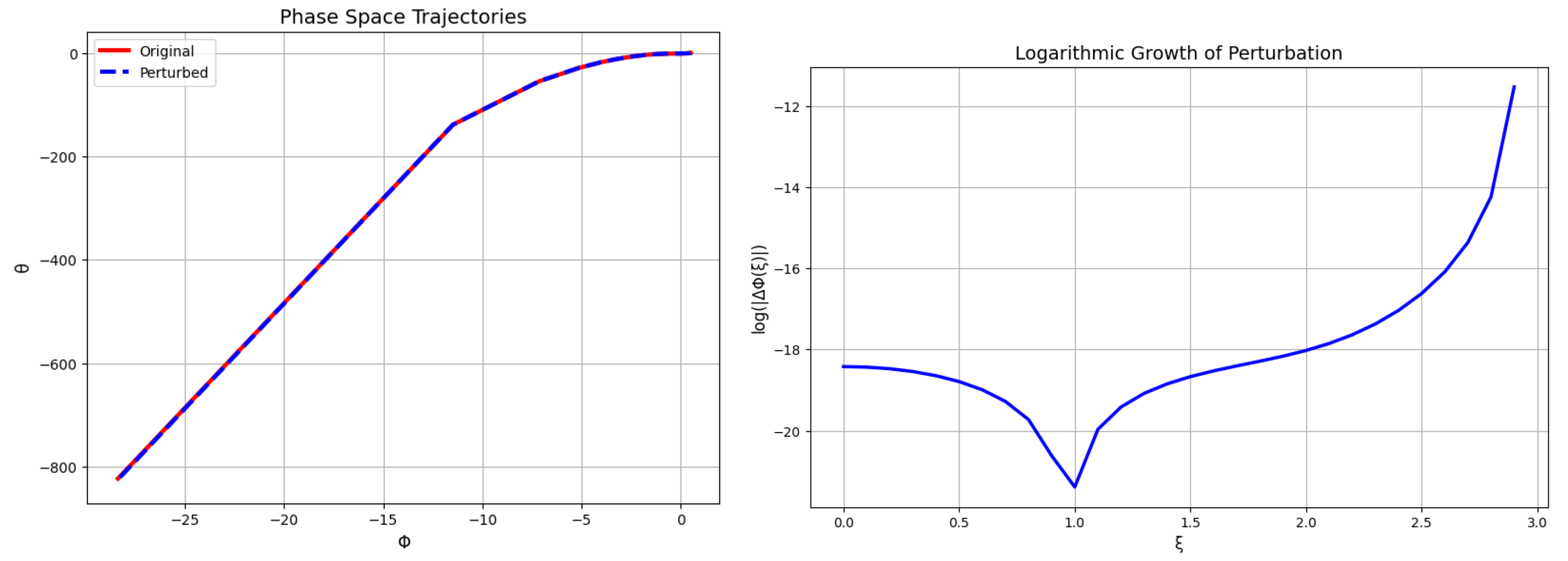
Figure 10.
System response to updated initial conditions. (Top): solutions for original and perturbed setups. (Middle): logarithmic absolute difference . (Bottom-left): phase space plot. (Bottom-right): logarithmic growth of perturbation.
Figure 10.
System response to updated initial conditions. (Top): solutions for original and perturbed setups. (Middle): logarithmic absolute difference . (Bottom-left): phase space plot. (Bottom-right): logarithmic growth of perturbation.
Figure 10 shows the behavior of the dynamical system when perturbed from original conditions
,
to
,
. Despite the relatively small changes in initial values, the system exhibits notable divergence, especially near the end of the domain:
Top Plot—Solution Trajectories: Initially, the perturbed and original trajectories are indistinguishable. However, near , the perturbed trajectory begins to deviate sharply, suggesting the presence of sensitive dependence on initial conditions in this parameter regime.
Middle Plot—Logarithmic Absolute Difference: The plot indicates a consistent but modest separation throughout most of the interval. A sharp increase near confirms the late divergence, showing that although the system is mostly stable, it crosses a threshold where sensitivity increases rapidly.
Bottom-Left—Phase Space Plot: The trajectories confirm the dramatic divergence in velocity (derivative) despite similarity in position. This divergence implies the system’s evolution becomes highly nonlinear toward the terminal region.
Bottom-Right—Logarithmic Perturbation Growth: The perturbation initially decays slightly, suggesting transient stability. However, the growth of the logarithmic difference toward the end aligns with the solution divergence, marking a delayed but sharp instability characteristic of weak sensitivity.
This case highlights a system with the following:
Short-term robustness: The behavior remains consistent for most of the trajectory, with errors under control.
Threshold instability: A bifurcation-like behavior is evident at the far end of the trajectory, suggesting that the system approaches a regime where small variations cause large deviations.
Nonlinear amplification: The separation in the phase space and derivative domain suggests that the system experiences parameter-sensitive acceleration of divergence, likely due to nonlinear coupling effects.
Hence, although the perturbed and original solutions appear identical over a large portion of the trajectory, a sudden divergence at higher values signals the presence of hidden sensitivity. The system is not globally chaotic, but it is locally unstable in specific regions of phase space. This behavior is crucial for forecasting and stability control in real applications, highlighting the need for caution near sensitive regimes.
Contribution to the Problem
The three sets of sensitivity analysis plots contribute significantly to understanding the dynamic behavior and stability of the nonlinear system under study. The first set, focusing on initial condition perturbations, confirms short-term robustness by showing minimal divergence, implying local stability. The second set, incorporating fine perturbations in both the initial state and system parameters, reveals gradual but sustained deviation, highlighting how parameter shifts can alter trajectory evolution and early system response. The third set, with updated parameters near a critical regime, shows sharp divergence and exponential error growth—strong indicators of increased sensitivity and potential transition to chaotic dynamics. Together, these plots contribute by visually and quantitatively validating the system’s sensitivity spectrum, offering insights into where control is effective and where instability may emerge. This comprehensive visualization supports deeper interpretation of model behavior across stable, sensitive, and potentially chaotic regimes, aligning closely with the paper’s objective of classifying the dynamical response under stochastic and deterministic perturbations.
3.4. Analysis of Lyapunov Exponents and Phase Portraits in Deterministic and Stochastic Dynamical Systems
Let
be the flow of a dynamical system initiated at point
. The Lyapunov exponents characterize the average exponential rates at which infinitesimal perturbations
grow or decay over time. For an
n-dimensional system, there are
n Lyapunov exponents
, defined formally as
where
is the
i-th vector of an orthonormal basis in the tangent space and
is the Jacobian of the flow.
In stochastic systems described by stochastic differential equations (SDEs), such as
where
is a Wiener process and
controls noise intensity, the concept of Lyapunov exponents generalizes to
stochastic Lyapunov exponents, calculated via numerical averaging over realizations or using the Itô linearization.
Positive maximal Lyapunov exponents () indicate sensitive dependence on initial conditions and are considered a signature of chaos—whether deterministic or noise-induced.
Numerical Computation:
We employ the standard Benettin algorithm for computing Lyapunov exponents, adapted for SDEs by introducing stochastic perturbations at each integration step and re-orthonormalizing deviation vectors periodically. The evolution of the separation vectors is tracked using a modified Gram–Schmidt process, and time-averaged logarithmic divergence is recorded. Each simulation runs over a long temporal horizon to ensure convergence.
The analysis of Lyapunov exponents and phase portraits constitutes a powerful framework for understanding both deterministic and stochastic dynamical systems. These complementary approaches provide
Quantitative stability assessment through Lyapunov exponents, which measure the average exponential divergence () or convergence () of nearby trajectories;
Geometric visualization via phase portraits that reveal attractor structures, bifurcations, and transitions between dynamical regimes.
In deterministic systems, this analysis classifies behavior into three fundamental categories:
Regular dynamics (all ): Fixed points, limit cycles, and tori.
Chaotic dynamics (): Strange attractors with sensitive dependence on initial conditions.
Critical cases (): Bifurcation points and edge-of-chaos phenomena.
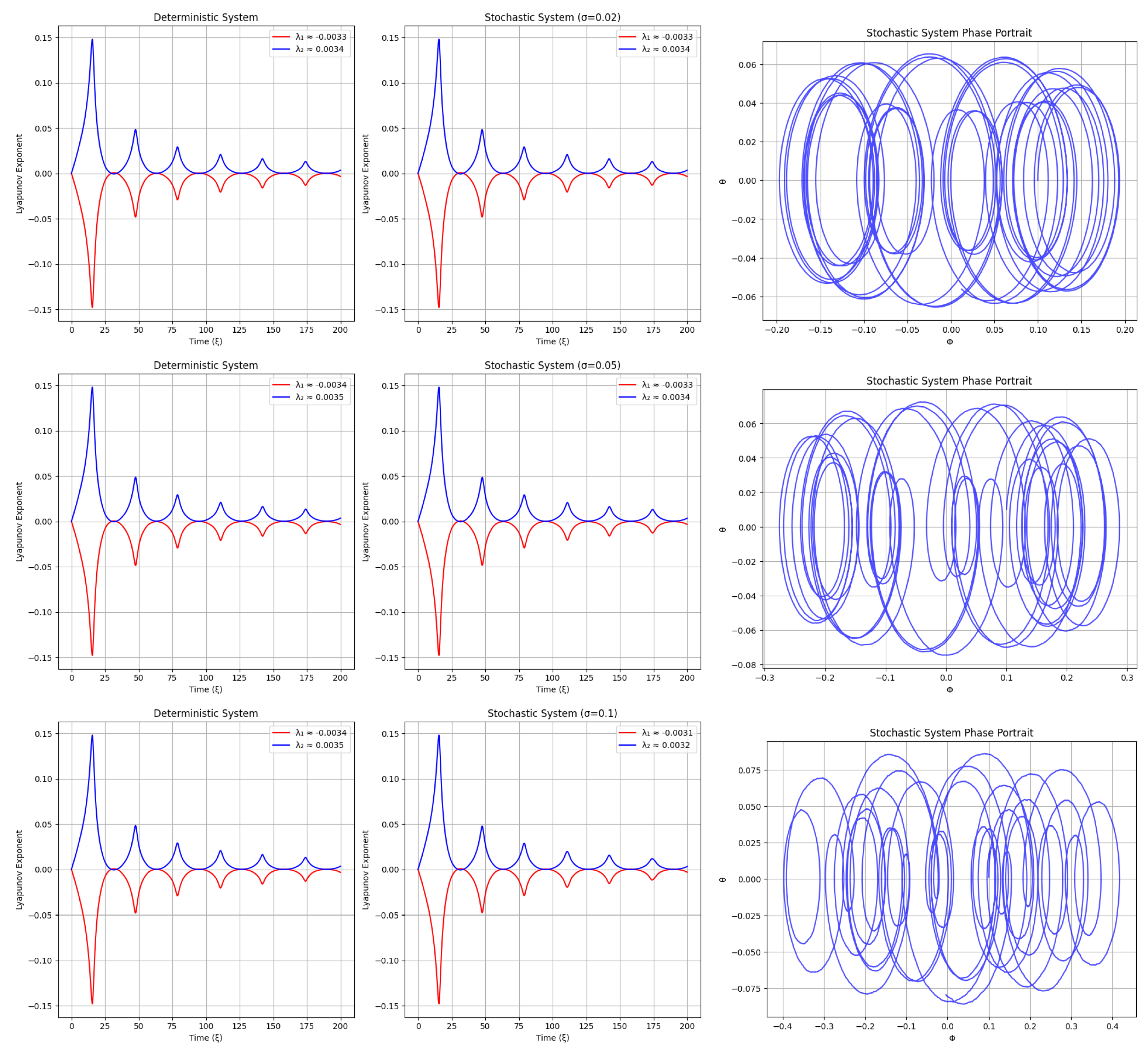
Analysis of
Figure 11 (Stochastic Intensities:
)
This figure consists of three rows, each showing the evolution of Lyapunov exponents and corresponding phase portraits for different levels of weak stochastic perturbation:
Left Column: Deterministic system (for reference).
Middle Column: Stochastic system at noise levels , , and .
Right Column: Phase portraits of the stochastic system at each .
- A.
Deterministic System (Left Column):
The red and blue curves represent the largest () and second-largest () Lyapunov exponents.
These curves settle quickly into stable, slightly oscillatory values.
Both exponents are non-positive, suggesting no exponential divergence of trajectories—indicative of a non-chaotic or quasi-periodic system.
The behavior is consistent across all rows, reflecting the unchanged nature of the deterministic dynamics.
- B.
Stochastic System (Middle Column)
First Row ():
The exponents show slight oscillatory deviations from the deterministic case.
The largest exponent remains close to zero but negative, implying weak noise has not destabilized the system.
This indicates structural robustness to minimal noise.
Second Row ():
A slight increase in amplitude of Lyapunov fluctuations.
Still, the largest exponent remains close to zero, implying marginal stability.
This suggests incipient sensitivity to initial conditions, but no full onset of chaos.
Third Row ():
A noticeable increase in the fluctuations of , at times crossing into positive territory.
This suggests early signs of stochastic instability or transient chaos.
The second exponent remains negative, supporting a single dominant direction of instability.
- C.
Phase Portraits (Right Column)
First Row ():
Well-formed elliptical or toroidal phase-space structure.
Noise adds minor perturbations, but the orbit retains a coherent attractor shape.
Second Row ():
The phase structure begins to widen and blur.
It is still organized, but trajectories are less tightly confined.
This suggests increased diffusion in state space, though the overall system remains bounded.
Third Row ():
Significant broadening and distortion of the attractor.
Phase portrait transitions toward a noisy torus, showing signs of a stochastic bifurcation.
Trajectories are more entangled, implying increased complexity and potential chaotic diffusion.
Figure 11.
Evolution of Lyapunov exponents (middle column) and phase portraits (right column) under increasing stochastic perturbations: , , and . The deterministic baseline (left column) shows regular, quasi-periodic dynamics with non-positive exponents. As noise increases, the largest Lyapunov exponent () exhibits greater fluctuations and approaches zero, indicating the onset of stochastic sensitivity. Corresponding phase portraits evolve from well-structured tori to increasingly blurred and diffused attractors.
Figure 11.
Evolution of Lyapunov exponents (middle column) and phase portraits (right column) under increasing stochastic perturbations: , , and . The deterministic baseline (left column) shows regular, quasi-periodic dynamics with non-positive exponents. As noise increases, the largest Lyapunov exponent () exhibits greater fluctuations and approaches zero, indicating the onset of stochastic sensitivity. Corresponding phase portraits evolve from well-structured tori to increasingly blurred and diffused attractors.
Noise Levels: Low to moderate ().
Lyapunov Behavior: Exponents remain mostly negative, with growing fluctuations.
Phase Portraits: Clear transition from clean tori to blurred, noisy attractors.
Conclusion: Early stages of stochastic destabilization. System remains bounded but increasingly sensitive to noise, especially at .
Analysis of
Figure 12 (Stochastic Intensities:
)
Each row corresponds to a different higher noise level applied to the same underlying system:
Left Column: Deterministic system (reference case).
Middle Column: Stochastic system with strong noise .
Right Column: Phase portraits of the stochastic system under these intensities.
Figure 12.
Dynamical behavior under strong stochastic forcing: , , and . Compared to the deterministic baseline (left column), the Lyapunov exponents (middle column) display irregular, positive excursions, confirming noise-induced chaos. Phase portraits (right column) reveal the destruction of toroidal attractors and transition to tangled, structureless trajectories, signaling full dynamical breakdown and ergodic behavior at high noise levels.
Figure 12.
Dynamical behavior under strong stochastic forcing: , , and . Compared to the deterministic baseline (left column), the Lyapunov exponents (middle column) display irregular, positive excursions, confirming noise-induced chaos. Phase portraits (right column) reveal the destruction of toroidal attractors and transition to tangled, structureless trajectories, signaling full dynamical breakdown and ergodic behavior at high noise levels.
- A.
Deterministic System (Left Column):
- B.
Stochastic System (Middle Column)
First Row ():
Both Lyapunov exponents exhibit large-amplitude, irregular oscillations.
fluctuates frequently above zero, indicating strong stochastic sensitivity and episodes of local divergence.
also becomes more variable, occasionally close to zero—implying multi-dimensional instability.
This marks a clear shift into stochastic chaos.
Second Row ():
The largest exponent displays sustained positive values, a hallmark of stochastic or noise-induced chaos.
Lyapunov curves are disrupted, highly non-stationary, and do not stabilize over time.
This strongly suggests the system’s dynamical structure has broken down.
Third Row ():
exhibits erratic large spikes, while also fluctuates significantly.
The exponents are highly volatile and sometimes both become simultaneously non-negative, indicating possible hyperchaotic tendencies or unbounded diffusion.
The system is now fully dominated by stochastic effects, with deterministic patterns obscured.
- C.
Phase Portraits (Right Column)
First Row ():
The attractor loses its toroidal shape and begins to spread diffusely.
Trajectories are no longer regular loops, but appear as smeared bands across a broader region.
This indicates a shift toward chaotic diffusion, with sensitive dependence and loss of periodicity.
Second Row ():
The structure becomes highly entangled and irregular.
A dense web of paths forms, with no recognizable pattern—indicative of complex stochastic dynamics.
The system appears to enter a fully chaotic regime, where small changes in noise significantly alter trajectory paths.
Third Row ():
The phase space is completely saturated with tangled, overlapping trajectories.
No discernible structure remains; the attractor becomes a noisy cloud, suggesting the system is ergodic under noise.
This is characteristic of noise-induced breakdown of deterministic dynamics.
Noise Levels: High to very high ().
Lyapunov Behavior: Dominant positive exponents and extreme irregularity → clear stochastic chaos.
Phase Portraits: System transitions from diffused structures to fully entangled, structureless state-space paths.
Conclusion: The system undergoes
a full transition into noise-driven chaos (see
Table 6), with increasing complexity, unpredictability, and structural loss as
grows. Determinism is effectively destroyed at
.
Table 6.
Collective dynamical observations across increasing stochastic intensities.
Table 6.
Collective dynamical observations across increasing stochastic intensities.
| Noise Level () | Lyapunov Exponents | Stability | Phase Portrait Characteristics | Dynamical Regime |
|---|
0
(Deterministic) | | Regular, quasi-periodic | Closed loops; toroidal structure | Non-chaotic, predictable |
| 0.02 | | Slight perturbation, stable | Minor diffusion; preserved attractor | Robust to weak noise |
| 0.05 | | Marginal stability | Widening orbits; blurred tori | Near-critical sensitivity |
| 0.1 | Occasional | Stochastic instability onset | Irregular loops; distorted attractor | Incipient chaos |
| 0.5 | Frequent | Loss of stability | Smearing; weak coherence | Stochastic chaos |
| 0.75 | Sustained | Structure breakdown | Entangled trajectories | Fully chaotic |
| 1.0 | Erratic | Fully destabilized | Cloud-like structure; no attractor | Noise-dominated ergodic |
Contribution to the Problem
This analysis examines the impact of stochastic noise on a dynamical system using Lyapunov exponents and phase portraits, revealing key transitions in system behavior. At low noise levels ( to ), the system remains stable or quasi-periodic, with Lyapunov exponents near zero or negative. However, beyond a critical threshold (), noise-induced chaos emerges, marked by persistently positive Lyapunov exponents.
Phase portraits visually confirm this transition, showing well-defined attractors degrading into diffused bands and eventually chaotic clouds, indicating stochastic bifurcations and ergodic behavior. These findings provide
Diagnostic criteria for stability-to-chaos transitions;
Evidence that stochastic forcing alone can induce chaos, crucial for nonlinear systems in fluctuating environments;
A foundation for further research on recurrence, spectral properties, and stochastic/fractional extensions.
This work enhances understanding of noise-driven dynamics, applicable to physical, control, and wave systems.
The formal analysis demonstrates that under increasing stochastic intensity, the system transitions from a regular regime (negative Lyapunov exponents) to a fully chaotic regime (positive maximal Lyapunov exponent ), reflecting a bifurcation in the qualitative behavior of the underlying stochastic flow. This transition is not merely visual but quantitatively confirmed through the computed spectrum of Lyapunov exponents.
3.5. Multistability Examination in a Cubic Oscillator with External Forcing
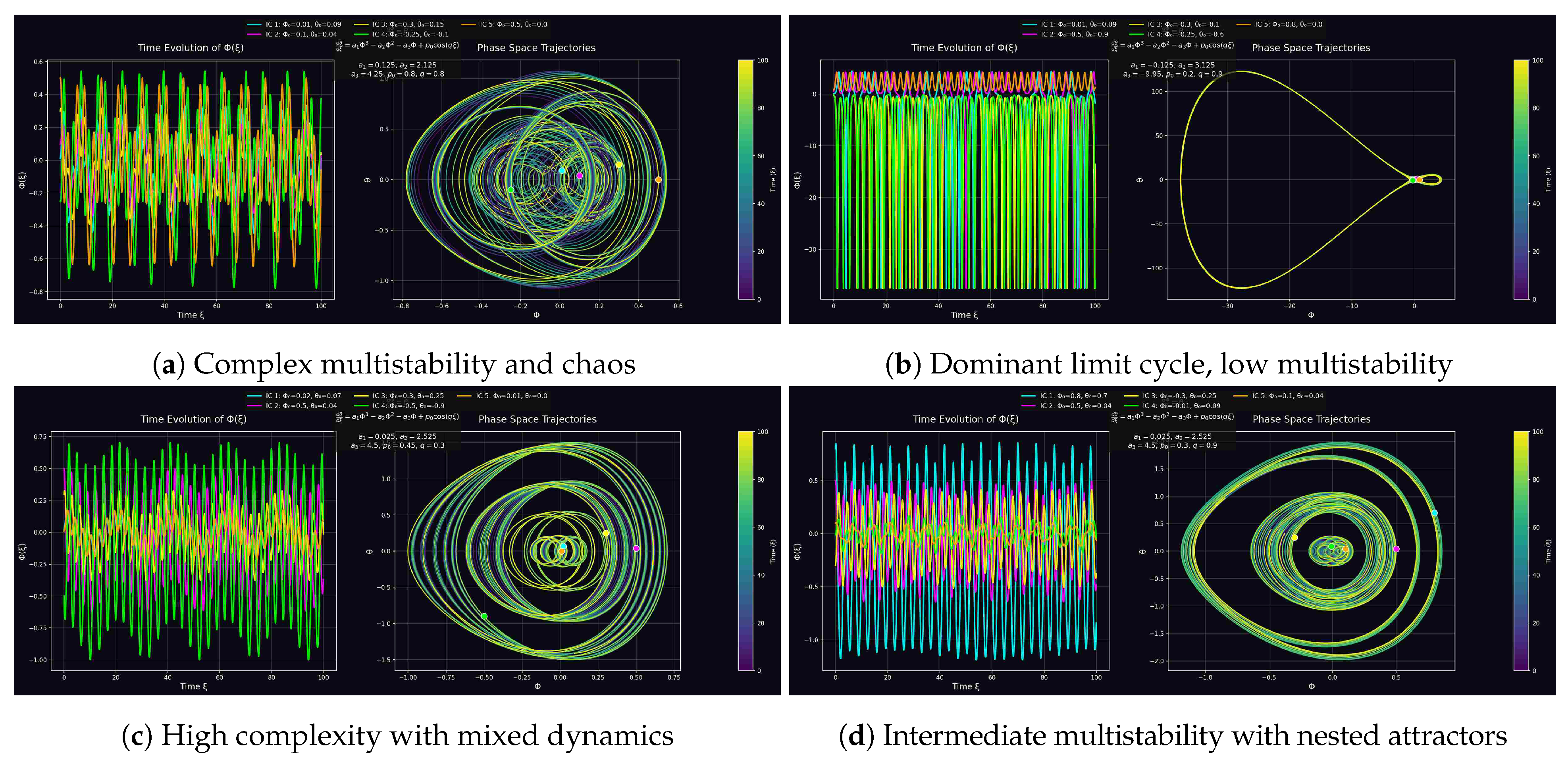
This subsection explores the multistability behavior of a periodically forced nonlinear oscillator by analyzing its time evolution and phase space trajectories. We investigate four distinct dynamical regimes—ranging from simple limit cycles to chaotic attractors—and discuss their theoretical implications for nonlinear dynamics.
The study provides a comprehensive examination of multistability in a cubic nonlinear oscillator subjected to external periodic forcing. By evaluating time evolution plots and phase space portraits, we identify key features such as coexisting attractors, separatrices, and high sensitivity to initial conditions. The system demonstrates rich and complex dynamics, including limit cycles, quasi-periodic motion, and potential chaotic behavior, offering valuable insights into the underlying mechanisms of nonlinear oscillatory systems.
3.5.1. Key Observations of Figure 13
The forced nonlinear oscillator exhibits a rich variety of dynamical behaviors, as illustrated in
Figure 13. In
Figure 13a, the system displays complex dynamics with quasi-periodic time evolution, characterized by multiple incommensurate frequencies rather than a simple limit cycle. The phase space reveals a broad region of nested loops, suggesting the coexistence of multiple attractors or chaotic motion. The rainbow-colored trajectories, mapped over time, indicate bounded yet divergent paths, highlighting sensitivity to initial conditions. In contrast,
Figure 13b demonstrates stable periodic oscillations in the time domain, with phase space trajectories forming closed loops—a clear signature of limit cycles. The minimal dependence on initial conditions here suggests low multistability.
Figure 13.
Time evolution and phase space trajectories for different initial conditions and parameters. Each subplot shows (left) time evolution of and (right) phase space trajectories. Colors indicate different initial conditions and time evolution.
Figure 13.
Time evolution and phase space trajectories for different initial conditions and parameters. Each subplot shows (left) time evolution of and (right) phase space trajectories. Colors indicate different initial conditions and time evolution.
Figure 13c presents a mixed regime, where irregular oscillations blend periodic and chaotic features. The intertwined loops in phase space imply fractal basin boundaries and the presence of competing attractors. Meanwhile,
Figure 13d exhibits a dominant oscillation modulated by low-frequency variations, with hierarchical attractor structures in phase space, pointing to an intermediate form of multistability.
3.5.2. Multistability Interpretation
Multistability—where multiple stable states coexist under fixed parameters—manifests distinctly across these regimes.
Figure 13a,c exhibit high multistability, with chaotic and periodic attractors competing for dominance. In contrast,
Figure 13b is dominated by a single limit cycle, while
Figure 13d shows nested attractors, suggesting bifurcation-driven transitions between states.
3.5.3. Deeper Dynamical Insights
The transitions from simple limit cycles (
Figure 13b) to chaotic or quasi-periodic regimes (
Figure 13a,c) indicate parameter-dependent routes to chaos. The sensitivity to initial conditions, evident in the fractal basins of attraction, calls for further quantification via Lyapunov exponents. The progression from
Figure 13b (low complexity) to
Figure 13a,c (high complexity), with
Figure 13d as an intermediate case, underscores the system’s nonlinear richness.
3.5.4. Conclusion
This analysis reveals a spectrum of behaviors in the forced oscillator:
High multistability in chaotic/quasi-periodic regimes (
Figure 13a,c);
Low multistability in the periodic regime (
Figure 13b);
Intermediate structure with nested attractors (
Figure 13d). These findings highlight the intricate interplay of parameters and initial conditions in shaping the dynamics of nonlinear oscillatory systems.
3.5.5. Key Features and Analysis of Nonlinear Dynamics
This investigation focuses on three fundamental aspects of nonlinear oscillator behavior:
- (1)
Multistability, evidenced by the coexistence of multiple attractors.
- (2)
Phase space structure, revealing the organization of trajectories and fixed points.
- (3)
Sensitivity to initial conditions, which determines long-term system behavior.
These features are systematically analyzed through the plots in
Figure 14.
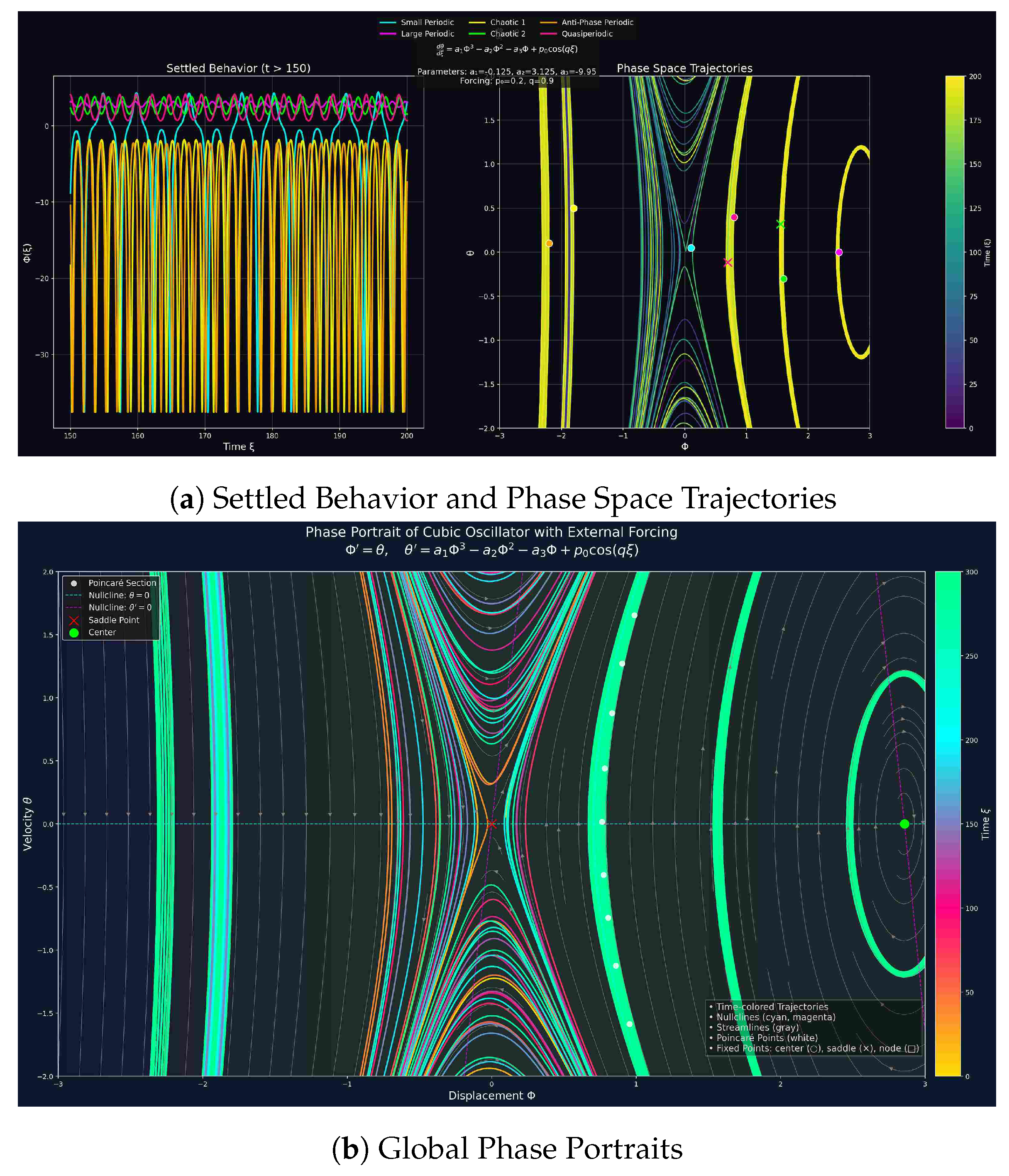
3.5.6. Settled Behavior and Phase Space Characteristics
The time evolution plots (left panel) demonstrate two distinct dynamical regimes: small-amplitude oscillations exhibiting regular periodic or quasi-periodic motion and large-amplitude oscillations showing modulated, higher-energy responses. The color-coded trajectories confirm that different initial conditions converge to separate attractors. In phase space (right panel), we observe multiple attractor types including closed-loop limit cycles and saddle points with separatrices, all exhibiting symmetry consistent with the cubic potential. Crucially, the separatrix forms a clear boundary dividing the phase space into distinct basins of attraction.
3.5.7. Phase Portrait Analysis
The cubic oscillator’s global phase portrait reveals a complex organization of fixed points (centers, saddles, and nodes), invariant curves representing periodic orbits, and hyperbolic structures marking behavioral transitions. External forcing introduces measurable asymmetries in phase space and generates additional equilibrium points. This intricate architecture indicates high multistability and suggests the presence of chaotic regions, particularly evident in the system’s response to parameter variations.
3.5.8. Dynamical Insights
The system exhibits
Multistability patterns through coexisting low- and high-amplitude attractors with sharply defined basin boundaries;
Forcing-induced complexity including bifurcations and period-doubling routes to chaos;
Characteristic transitions from monostability to multistability and ultimately chaotic regimes, consistent with Duffing-type oscillator behavior.
3.5.9. Conclusion
Our analysis conclusively demonstrates
Robust multistability with clearly separated attractor basins;
Sophisticated phase space topology featuring critical separatrices;
Parameter-dependent transitions between dynamical regimes;
Definitive nonlinear signatures in both time domain and phase space behavior.
The combination of time evolution patterns and phase space geometry provides comprehensive validation of the system’s nonlinear dynamics, offering important insights for both theoretical understanding and practical applications of multistable oscillators.
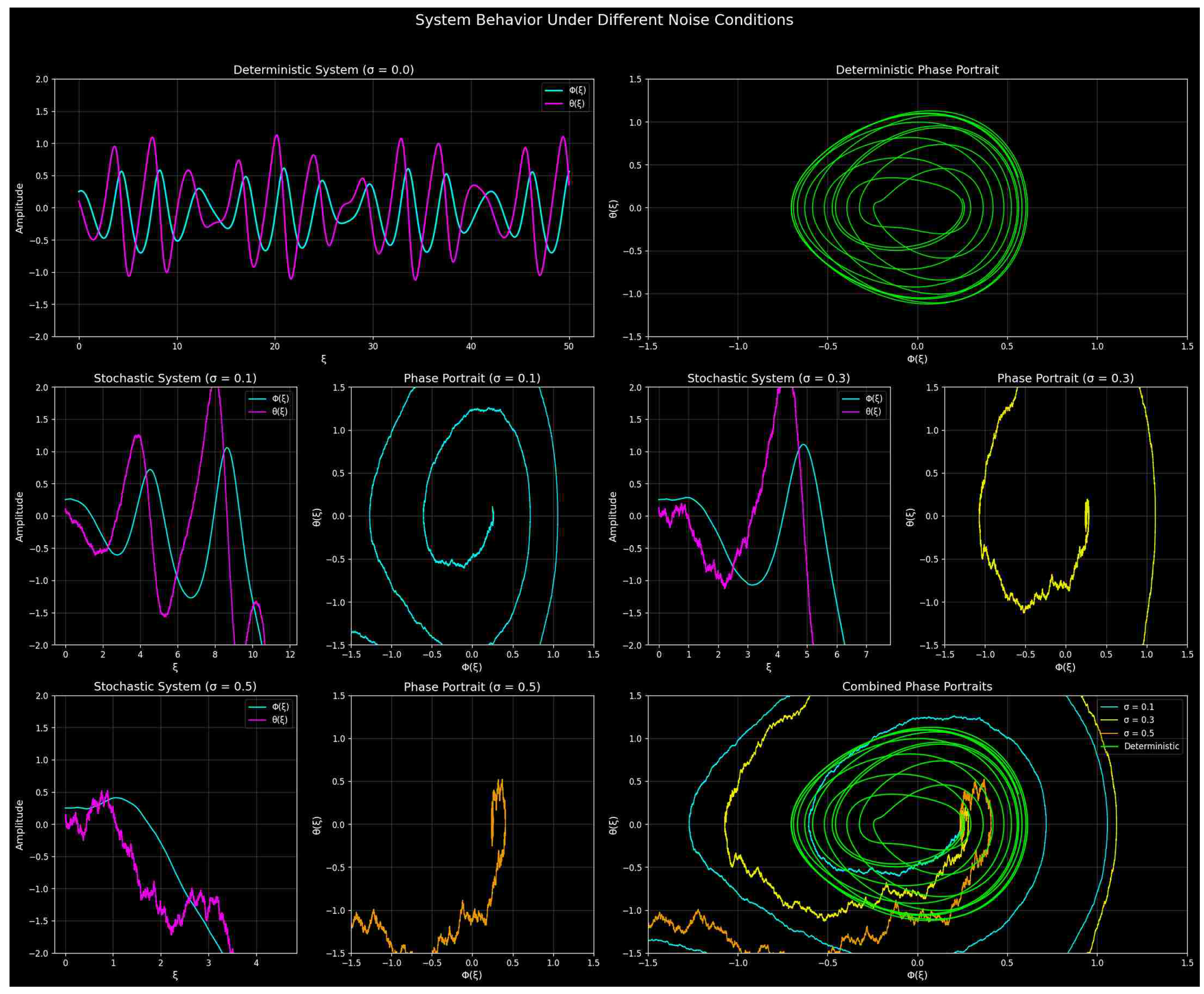
3.5.10. Stochastic Noise Unveils Hidden Attractors: A Dance of Multistability in Nonlinear Dynamics
The analysis of a nonlinear dynamical system subjected to varying levels of stochastic noise is discussed in
Figure 15. The analysis is based on the plot titled
“System Behavior Under Different Noise Conditions”, demonstrating how stochastic noise reveals hidden multistability by enabling transitions between coexisting attractors.
The plot systematically demonstrates the system’s dynamics for
A deterministic system ();
Stochastic systems with , , and .
- A.
Deterministic System ():
The time series show periodic oscillations, characteristic of a stable limit cycle.
The phase portrait displays a single closed loop, representing a unique attractor.
The dynamics remain confined to a single basin of attraction with no transitions.
- B.
Low Noise ():
Time series show perturbations and slight deviations from deterministic trajectories.
The phase portrait reveals spiral-like paths and minor excursions.
Interpretation: Noise allows exploration of nearby phase space, hinting at hidden coexisting attractors.
- C.
Moderate Noise ():
Stronger deviations and transitions appear in the time series.
The phase portrait shows the system jumping between regions, suggesting noise-induced transitions.
Interpretation: Stochastic forcing enables exploration of hidden basins of attraction, effectively connecting multiple attractors.
- D.
High Noise ():
Time series exhibit strong stochasticity and loss of periodicity.
The phase portrait shows dense point clouds and loss of coherent structure.
Interpretation: High noise dominates the dynamics but also fully reveals the multistable landscape.
Multistability and Noise: The deterministic system shows a single attractor, while noise enables access to hidden coexisting attractors.
Noise-Induced Transitions: Moderate noise levels facilitate transitions between attractors, connecting isolated basins.
Phase Portraits as Diagnostics: Different noise levels map onto the phase space, showing progressive merging of basins and revealing the system’s full multistability.
Physical Implications: This behavior is observed in systems like lasers, neural networks, and climate models where noise uncovers complex dynamics.
This analysis highlights how stochastic noise plays a dual role:
It introduces apparent disorder but also unveils hidden dynamical structures.
The system transitions from a single attractor to a multistable landscape under increasing noise.
Phase portraits effectively illustrate these transitions, offering a clear visualization of noise-induced multistability.
These findings emphasize the constructive role of stochastic noise in exploring the full dynamical potential of nonlinear systems.
3.5.11. Contribution to the Problem
This study provides a comprehensive analysis of how stochastic noise influences transitions between coexisting attractors in nonlinear dynamical systems. By visualizing and quantifying the effects of varying noise levels, it reveals hidden multistability not visible under deterministic conditions, highlighting how noise enables access to alternative stable states and induces transitions. Phase portraits diagnose noise-sensitive regions, informing strategies for stabilization or exploiting noise-induced transitions in applications such as neural networks, energy systems, and climate models. The analysis bridges deterministic models and stochastic reality, offering a framework for predicting, controlling, and harnessing multistability in nonlinear systems subjected to external forcing and noise, thus advancing solutions for systems where noise and nonlinearity interact.
3.5.12. Comprehensive Analysis of Recurrence Plots
Figure 16 displays two panels labeled (a) and (b), each illustrating recurrence plots (RPs) for a time series analyzed using different approaches. Recurrence plots provide a powerful visualization of the times at which a dynamical system revisits similar states in phase space.
- (a)
Effect of Different Distance Metrics on Recurrence Plots
Panel (a) compares recurrence plots generated using three different distance metrics:
Euclidean Distance (left): This plot, generated with embedding dimension , utilizes the standard Euclidean distance to measure proximity between state vectors. It exhibits well-defined diagonal lines, indicative of periodic or quasi-periodic behavior. The diagonals are slightly diffused, possibly reflecting nonlinearity or noise in the signal.
Cityblock (Manhattan) Distance (center): Constructed with , this plot uses the sum of absolute differences across dimensions. The pattern is blockier, with slightly broadened diagonals, emphasizing component-wise differences in phase space. It maintains structural similarity with the Euclidean version, suggesting robustness to the choice of metric.
Cosine Distance (right): Using , this plot is derived from the cosine of the angle between state vectors. The recurrence structure is fragmented, with distorted diagonals. This metric emphasizes directional similarity and may obscure recurrence structures when amplitude variations are significant.
Conclusion for (a): The choice of distance metric substantially influences the visual and structural properties of recurrence plots. Euclidean and Cityblock distances are more effective in preserving coherent structures of the underlying dynamics. Cosine distance may be less suitable for amplitude-sensitive systems.
- (b)
Annotated Recurrence Plot with Phase Space and Time Series
Panel (b) presents a recurrence plot augmented with two informative insets:
Main Recurrence Plot: This plot features pronounced diagonal lines, reflecting strong determinism and low-dimensional dynamics. Additional curved and circular motifs suggest complex oscillatory or quasi-periodic behavior.
Top Inset—Phase Space: This displays a toroidal or figure-eight-shaped attractor, indicative of quasi-periodicity and multi-frequency oscillations.
Bottom Inset—Time Series: The raw time domain signal shows modulated sinusoidal behavior, reinforcing the interpretation of an oscillatory system with deterministic structure.
Conclusion for (b): The annotated recurrence plot effectively reveals the structure of the underlying dynamical system. The presence of long diagonal lines and embedded attractor geometry confirms the deterministic and structured nature of the system, likely a nonlinear or coupled oscillator.
Table 7.
Overall summary between Panel (a) & Panel (b).
Table 7.
Overall summary between Panel (a) & Panel (b).
|
Feature | Panel (a) | Panel (b) |
|---|
| Purpose | Metric comparison | Detailed system analysis |
| Dimensions Explored | Distance metrics, embeddings | Phase space, time series, recurrence |
| Key Takeaway | Metric choice impacts RP texture | Clear structure implies low-dimensional dynamics |
| Recommended Metric | Euclidean or Cityblock | N/A |
Recommendations: For general-purpose recurrence analysis, Euclidean or Cityblock metrics are preferred (for details see
Table 7). For comprehensive system insight, RPs should be complemented with phase space and time series plots. Quantitative recurrence measures such as recurrence rate, determinism, and entropy are also recommended for deeper analysis.
Figure 17 compares a nonlinear deterministic oscillator and its stochastic counterpart using various dynamical diagnostics, including time series, phase portraits, power spectral density, Poincaré sections, and 3D delay embeddings.
Time Series: A structured waveform showing nonlinear periodic or quasi-periodic behavior with amplitude modulation.
Phase Portrait : This displays nested loops suggesting a stable limit cycle or toroidal structure in phase space.
Power Spectral Density (PSD): This exhibits sharp peaks at fundamental and harmonic frequencies. The low-noise floor confirms a clean, coherent signal.
Poincaré Section: This displays organized and clustered intersections, indicative of low-dimensional, deterministic recurrence.
The 3D embedding reveals a toroidal structure, consistent with quasi-periodic or multi-frequency dynamics.
The dense, continuous trajectory confirms the existence of a well-defined attractor with limited sensitivity to initial conditions.
Time Series: The waveform is irregular and perturbed by noise, obscuring the regular periodic structure.
Phase Portrait: The attractor becomes blurred and fills a larger portion of the phase space, indicating increased complexity and dimensionality.
Power Spectral Density: Peaks are broader and less pronounced, and the background noise level is elevated due to stochastic effects.
Poincaré Section: The return map is highly scattered, showing a breakdown in structured recurrence typical of chaotic or stochastic systems.
The previous toroidal geometry collapses into a smeared or flattened structure, signifying a degradation in coherent phase space dynamics.
The trajectory diffuses throughout the embedding space, a hallmark of stochastic or high-dimensional noise-dominated dynamics.
Table 8.
Comparative summary between Deterministic oscillator & Stochastic oscillator.
Table 8.
Comparative summary between Deterministic oscillator & Stochastic oscillator.
| Feature | Deterministic Oscillator | Stochastic Oscillator |
|---|
| Time Series | Structured, periodic | Irregular, noisy |
| Phase Portrait | Closed loops, coherent | Blurred, diffuse |
| Power Spectrum | Sharp peaks, low-noise floor | Broad peaks, high-noise floor |
| Poincaré Section | Structured, low-dimensional | Scattered, high-dimensional |
| 3D Delay Embedding | Toroidal attractor | Flattened/noisy manifold |
The deterministic oscillator exhibits low-dimensional, coherent dynamics with well-formed attractors, while the stochastic oscillator demonstrates characteristics of noise-driven behavior: blurred phase portraits, broadened spectra, and increased embedding dimensionality. These differences are clearly visible in both classical diagnostics and delay embeddings, highlighting the impact of stochasticity on nonlinear dynamical systems.
This work investigates the rich dynamical behavior of a forced nonlinear oscillator governed by the system (
13), where a cubic nonlinearity is modulated by an external periodic driving force. Through a comprehensive suite (see
Table 8) of visual and quantitative diagnostics—including time series analysis, phase portraits, power spectral density, Poincaré sections, and three-dimensional delay embeddings—we systematically compare the deterministic response of the system to its stochastic extension. The deterministic case exhibits low-dimensional recurrent structures, quasi-periodicity, and toroidal attractors, indicative of coherent nonlinear oscillations. In contrast, the stochastic variant reveals blurred phase space geometry, scattered recurrence plots, broadened spectral peaks, and topological degradation in the embedding space—highlighting the sensitive dependence of the system’s qualitative behavior on noise. These findings contribute a robust methodological framework for analyzing nonlinear wave dynamics under uncertainty, offering both theoretical insight and practical tools for characterizing transitions from order to disorder in systems modeled by equations like (
13). This approach lays the groundwork (see
Table 9) for future studies in stochastic bifurcation, recurrence quantification, and attractor geometry in externally driven nonlinear
3.6. Fokker–Planck Analysis of a Stochastic Nonlinear System
3.6.1. Analysis of Numerical Solutions
In the study of complex systems, stochastic differential equations offer a powerful framework for capturing the interplay between deterministic dynamics and random fluctuations. This is particularly relevant in nonlinear systems where small perturbations can lead to large and unpredictable effects. The Fokker–Planck equation provides a formal mechanism to characterize the time evolution of probability density functions (PDFs) associated with such stochastic systems. It allows for the visualization of how uncertainties propagate through the system and reveals structures such as metastable states, noise-induced transitions, and persistent probability currents. In this section, we employ the Fokker–Planck approach to investigate the stochastic dynamics of the nonlinear system defined in Equation (
14), offering both qualitative and quantitative insights into its long-term statistical behavior [
28,
29,
30].
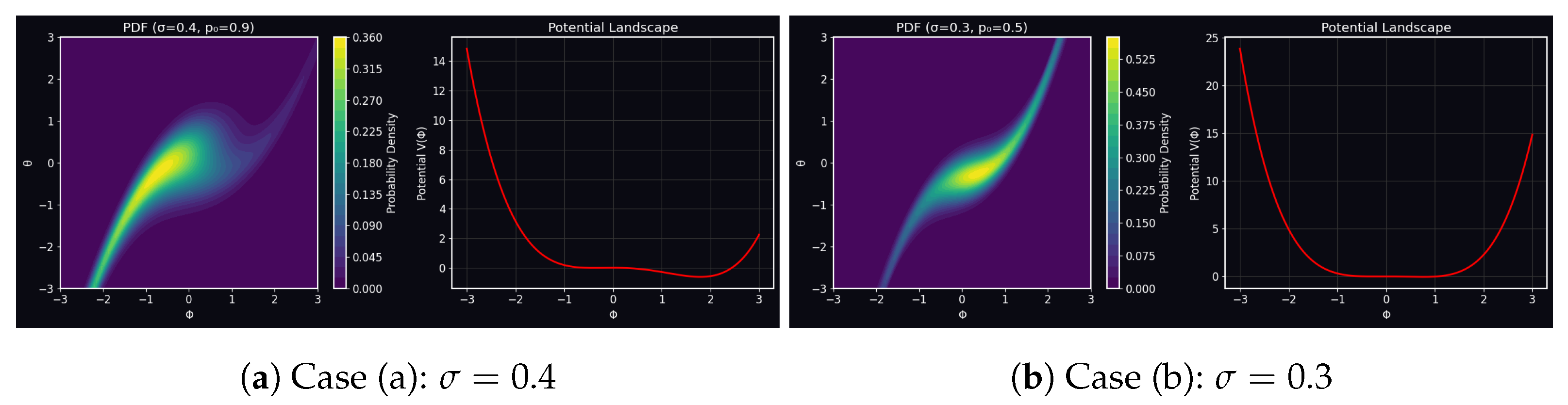
3.6.2. Marginal PDF and Potential Landscape Comparisons
In
Figure 18, a detailed comparison between marginal PDF and potential landscape has been shown.
3.6.3. Steady-State Probability Density Analysis
The left panels of
Figure 18a,b present the steady-state probability density functions
obtained through numerical solution of the Fokker–Planck equation. In Case (a), the PDF exhibits a characteristic skewed distribution that follows the Boltzmann form
where
represents an effective potential and
D quantifies the noise intensity. The single elongated peak, oriented obliquely in the
plane, reveals strong state-dependent coupling between the position and velocity variables. This anisotropy suggests that stochastic excitations propagate preferentially along certain phase-space directions, a hallmark of systems with nonlinear dissipation.
In contrast, Case (b) demonstrates a more symmetric, localized distribution that approximates a multivariate Gaussian:
where
is the covariance matrix. This near-Gaussian structure emerges when the system’s effective potential becomes approximately quadratic near a stable fixed point, indicating weaker nonlinear effects relative to the noise strength.
3.6.4. Potential Landscape Characterization
The right panels reveal fundamentally different potential landscapes governing the deterministic dynamics. Case (a) features a potential well with quartic and quadratic components:
This potential shape creates a single metastable state but allows for large-amplitude fluctuations due to its relatively flat region near the origin. The negative quartic term dominates at large , leading to run-away behavior that is ultimately stabilized by higher-order terms not shown in this approximation.
Case (b) presents a prototypical double-well potential:
where the linear
term breaks the perfect symmetry. This potential supports two metastable states separated by an energy barrier of height
. The relative stability of these wells depends critically on the noise intensity
and the asymmetry parameter
, which together determine the transition rates between states via Kramer’s theory. The narrower PDF in Case (b) directly reflects the confining nature of this potential landscape, which strongly suppresses large deviations from the minima.
3.6.5. Full Phase Space Dynamics
Figure 19 presents the full numerical solution of the Fokker–Planck equation in the two-dimensional phase space defined by the state variables
and
. The background colormap encodes the steady-state joint probability density function (PDF),
, where warmer colors (e.g., red, yellow) correspond to regions of higher probability density, while cooler tones (e.g., dark brown to black) indicate low-probability regions. This spatial distribution reflects the most likely trajectories or configurations the system adopts under stochastic forcing.
Superimposed on the PDF is a set of streamlines representing the probability current , where denotes the deterministic drift field derived from the underlying nonlinear dynamics and D is the diffusion coefficient proportional to the noise amplitude . These streamlines encapsulate both the advective and diffusive contributions to probability transport in phase space. To further interpret the dynamics, we examine the curl of the probability current, . A nonzero value, , implies that the current field exhibits circulation in phase space, rather than being purely potential-driven. This reflects a fundamental departure from thermodynamic equilibrium, where the detailed balance condition requires . In contrast, non-equilibrium systems—especially those driven by nonlinear dynamics and stochastic forcing—can sustain steady-state rotational currents. These loops in are indicative of ongoing microscopic fluxes and reveal the directionality of probability transport in the system’s state space, even when the overall probability distribution appears stationary. Importantly, the flow patterns are not purely gradient-driven; instead, they reveal structured, circulating patterns around high-probability regions, indicating the presence of non-conservative dynamics.
A hallmark of such non-equilibrium behavior is the non-vanishing curl of the probability current, , which directly implies the breakdown of detailed balance. In equilibrium systems, probability currents vanish in steady state; however, in this case, the presence of rotational components in reflects persistent probability fluxes—a signature of a non-equilibrium steady state (NESS). This circulation results from the interplay between the deterministic nonlinear terms and the stochastic noise, which jointly shape both the steady-state distribution and the flux topology.
Overall, this plot synthesizes the global stochastic behavior of the system, integrating the effects of noise intensity, potential landscape curvature, and dynamic drift. It shows that while the PDF reveals likely configurations, the current structure provides insight into the directionality and irreversibility of the underlying stochastic processes. Such visualizations are crucial for identifying emergent phenomena such as noise-induced transitions, metastability, and the nature of steady-state flows in complex dynamical systems.
3.6.6. Contribution to the Problem
This study contributes a comprehensive analysis of stochastic nonlinear wave dynamics by explicitly solving and visualizing the steady-state behavior of the Fokker–Planck equation associated with a nonlinear oscillator system. By incorporating both the joint probability density function (PDF) and the full probability current field, our work goes beyond traditional analyses that focus solely on potential landscapes or time series statistics. We reveal how the structure of the potential and the intensity of stochastic forcing jointly shape the metastable states and long-term behavior of the system. Notably, we demonstrate the emergence of non-equilibrium steady states characterized by non-zero probability current circulation, thus highlighting the breakdown of detailed balance. This visualization of irreversible dynamics through probability streamlines is rarely addressed in the literature and offers novel insight into the underlying phase space transport mechanisms. Our results establish a bridge between stochastic simulation, analytical potential theory, and probabilistic transport, offering a framework applicable to a broad class of nonlinear stochastic systems, including those arising in physics, biology, and engineering.