Rapid Estimation of Soil Copper Content Using a Novel Fractional Derivative Three-Band Index and Spaceborne Hyperspectral Data
Abstract
1. Introduction
2. Materials and Methods
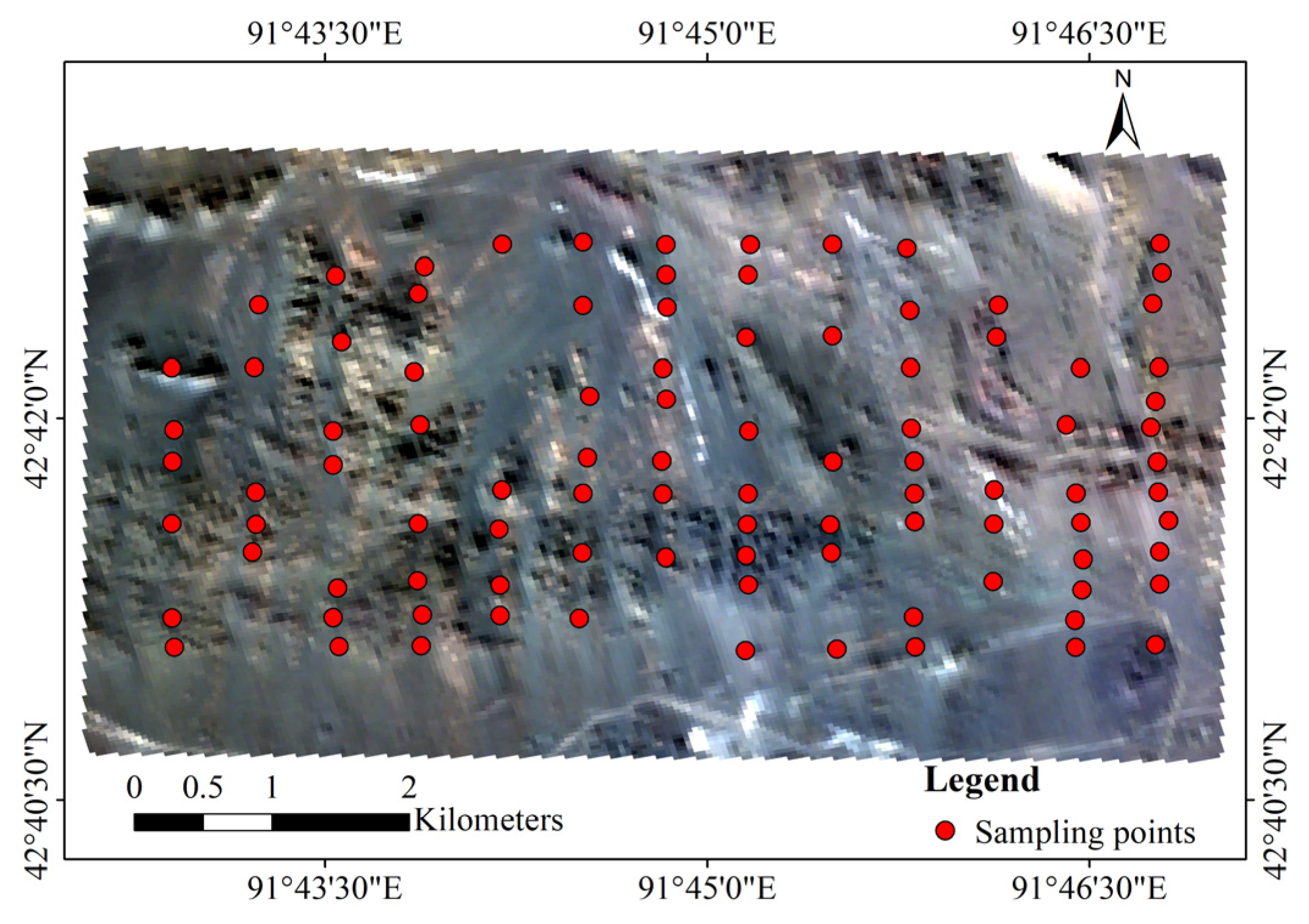
2.1. Study Area
2.2. Soil Sample Collection and Copper Content Measurements
2.3. GF-5 Hyperspectral Data Acquisition and Preprocessing
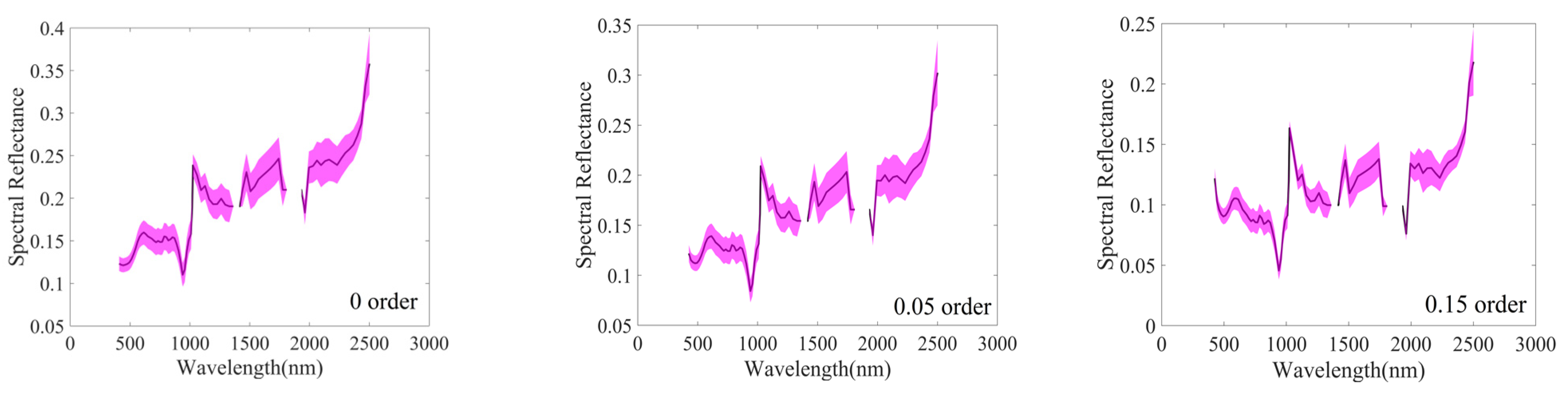
2.4. Fractional-Order Derivative
2.5. Establishing the Three-Band Spectral Index
2.6. Model Establishment and Evaluation
3. Results
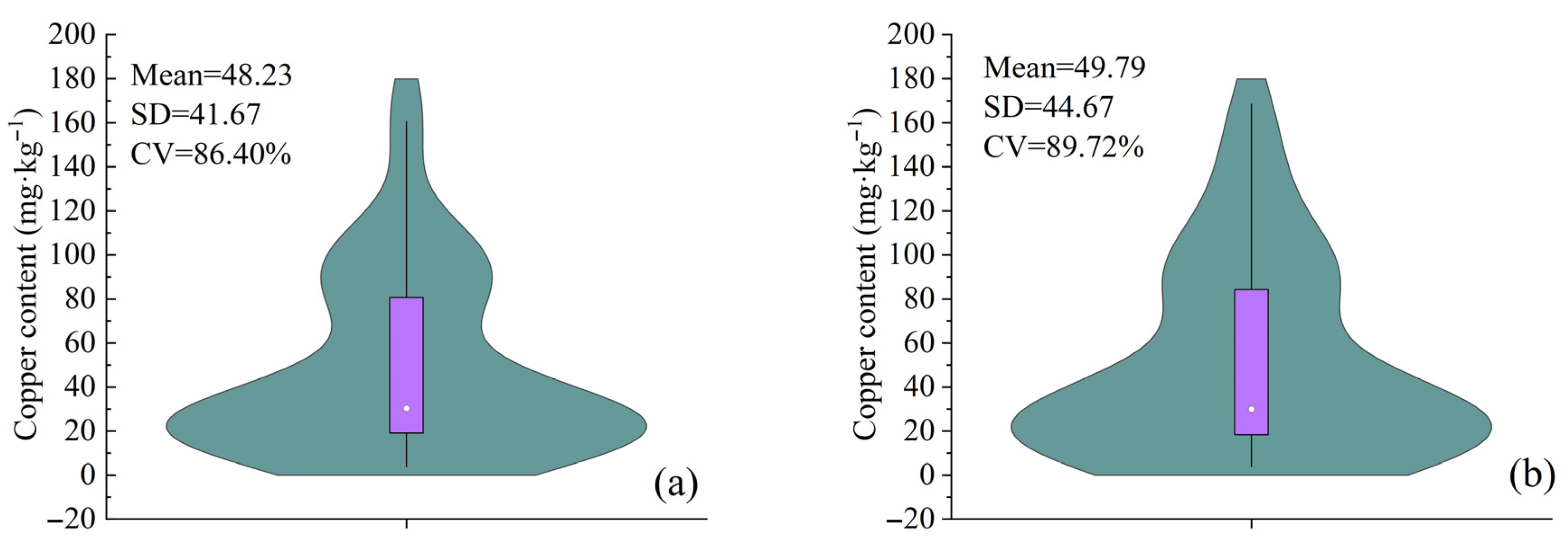
3.1. Soil Copper Content
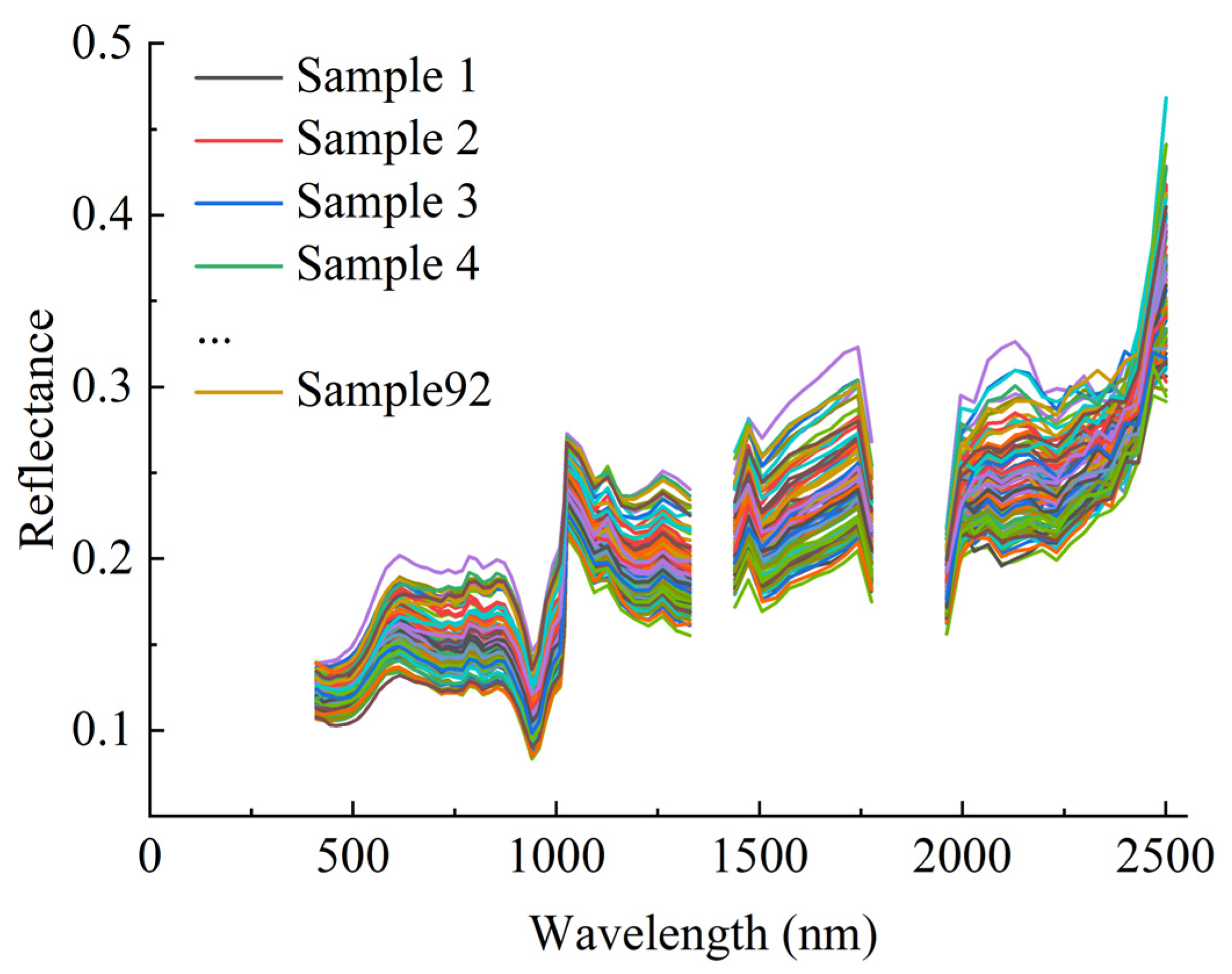
3.2. Spectral Characteristics
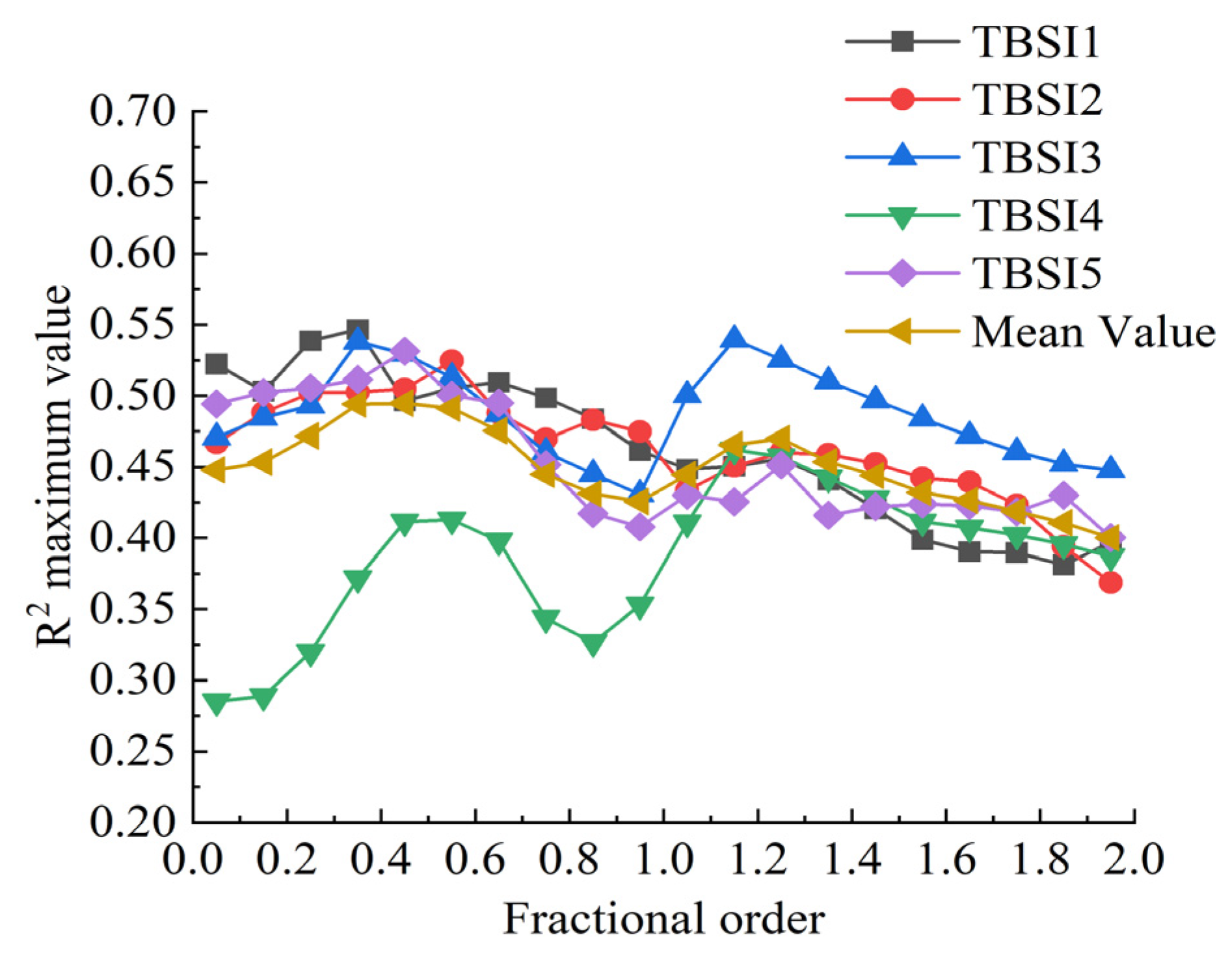
3.3. Optimal Three-Band Spectral Index
3.4. Performance of Copper Content Estimation Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shi, T.Z.; Chen, Y.Y.; Liu, Y.L.; Wu, G.F. Visible and Near-Infrared Reflectance Spectroscopy—An Alternative for Monitoring Soil Contamination by Heavy Metals. J. Hazard. Mater. 2014, 265, 166–176. [Google Scholar] [CrossRef] [PubMed]
- Torres-Sallan, G.; Schulte, R.P.O.; Lanigan, G.; Byrne, K.A.; Reidy, B.; Simo, I.; Six, J.; Creamer, R.E. Clay Illuviation Provides a Long-Term Sink for C Sequestration in Subsoils. Sci. Rep. 2017, 7, 45635. [Google Scholar] [CrossRef] [PubMed]
- Habashi, J.; Moghadam, H.J.; Oskouei, M.M.; Pour, A.B.; Hashim, M. PRISMA Hyperspectral Remote Sensing Data for Mapping Alteration Minerals in Sar-e-Châh-e-Shur Region, Birjand, Iran. Remote Sens. 2024, 16, 1277. [Google Scholar] [CrossRef]
- Mahboob, M.A.; Celik, T.; Genc, B. Predictive Modelling of Mineral Prospectivity Using Satellite Remote Sensing and Machine Learning Algorithms. Remote Sens. Appl. Soc. Environ. 2024, 36, 101316. [Google Scholar] [CrossRef]
- Santos, D.; Azzalini, A.; Mendes, A.; Cardoso-Fernandes, J.; Lima, A.; Müller, A.C.; Teodoro, A. Optimizing Exploration: Synergistic Approaches to Minimize False Positives in Pegmatite Prospecting. Ore Geol. Rev. 2024, 175, 106347. [Google Scholar] [CrossRef]
- Ahmed, I.; Liu, H.F.; Chen, R.J.; Ahmad, J.; Shah, S.A.; Fahad, S.; Rahim, O.A.; Ullah, F.; Rui, L. Geothermal Resource Exploration in Reshi Town by Integrated Geophysical Methods. Energies 2024, 17, 856. [Google Scholar] [CrossRef]
- Halford, D.T.; Karolyte, R.; Dellenbach, J.T.; Cathey, B.; Cathey, M.; Balentine, D.; Andreason, M.W.; Rice, G.K. Applications in Utilizing Soil Gas Geochemistry Along with Geological and Geophysical Data to Construct Helium Exploration Statistical Models. Front. Earth Sci. 2024, 12, 1434785. [Google Scholar] [CrossRef]
- Sumanovac, F.; Kapuralic, J.; Pavicic, I.; Perkovic, L. Assessment of Near-Surface Geophysical Methods Used to Discover Karst Bauxite Deposits in the Dinarides Using the Example of Posušje Area, Bosnia and Herzegovina. Minerals 2024, 14, 378. [Google Scholar] [CrossRef]
- Henne, A.; Noble, R.R.P.; Williams, M. Multi-Element Geochemical Analyses on Ultrafine Soils in Western Australia—Towards Establishing Abundance Ranges in Mineral Exploration Settings. J. Geochem. Explor. 2024, 24, geochem2023-043. [Google Scholar] [CrossRef]
- Puchhammer, P.; Kalubowila, C.; Braus, L.; Pospiech, S.; Sarala, P.; Filzmoser, P. A Performance Study of Local Outlier Detection Methods for Mineral Exploration with Geochemical Compositional Data. J. Geochem. Explor. 2024, 258, 107392. [Google Scholar] [CrossRef]
- Sadeghi, B.; Molayemat, H.; Pawlowsky-Glahn, V. How to Choose a Proper Representation of Compositional Data for Mineral Exploration? J. Geochem. Explor. 2024, 259, 107425. [Google Scholar] [CrossRef]
- Cheng, Y.Y.; Zhou, K.F.; Wang, J.L.; Cui, S.C.; Yan, J.N.; De Maeyer, P.; Van de Voorde, T. Regional Metal Pollution Risk Assessment Based on a Long Short-Term Memory Model: A Case Study of the South Altai Mountain Mining Area, China. J. Clean. Prod. 2022, 379, 134755. [Google Scholar] [CrossRef]
- Buaisha, M.; Balku, S.; Özalp-Yaman, S. Heavy Metal Removal Investigation in Conventional Activated Sludge Systems. Civ. Eng. J. 2020, 6, 470–477. [Google Scholar] [CrossRef]
- Cheng, Y.Y.; Zhou, K.F.; Wang, J.L.; Cui, S.C.; Yan, J.N.; De Maeyer, P.; Van de Voorde, T. Regional Metal Pollution Risk Assessment Based on a Big Data Framework: A Case Study of the Eastern Tianshan Mining Area, China. Ecol. Indic. 2022, 145, 109585. [Google Scholar] [CrossRef]
- Liu, X.M.; Song, Q.J.; Tang, Y.; Li, W.L.; Xu, J.M.; Wu, J.J.; Wang, F.; Brookes, P.C. Human Health Risk Assessment of Heavy Metals in Soil-Vegetable System: A Multi-Medium Analysis. Sci. Total. Environ. 2013, 463, 530–540. [Google Scholar] [CrossRef]
- Mwesigye, A.R.; Young, S.D.; Bailey, E.H.; Tumwebaze, S.B. Population Exposure to Trace Elements in the Kilembe Copper Mine Area, Western Uganda: A Pilot Study. Sci. Total. Environ. 2016, 573, 366–375. [Google Scholar] [CrossRef]
- Hofer, C.; Borer, F.; Bono, R.; Kayser, A.; Papritz, A. Predicting Topsoil Heavy Metal Content of Parcels of Land: An Empirical Validation of Customary and Constrained Lognormal Block Kriging and Conditional Simulations. Geoderma 2013, 193, 200–212. [Google Scholar] [CrossRef]
- Francos, N.; Gholizadeh, A.; Ben Dor, E. Spatial Distribution of Lead (Pb) in Soil: A Case Study in a Contaminated Area of the Czech Republic. Geomat. Nat. Hazards Risk 2022, 13, 610–620. [Google Scholar] [CrossRef]
- Duru, S.C.; Echiegu, E.A.; Anyadike, C.C.; Alaneme, G.U.; Okechukwu, M.E. Spatial Variability of Heavy Metals Concentrations in Soil of Auto-Mechanic Workshop Clusters in Nsukka, Nigeria. Sci. Rep. 2024, 14, 9681. [Google Scholar] [CrossRef] [PubMed]
- Chandra, K.; Proshad, R.; Islam, M.; Idris, A.M. An Integrated Overview of Metals Contamination, Source-Specific Risks Investigation in Coal Mining Vicinity Soils. Environ. Geochem. Health 2023, 45, 7425–7458. [Google Scholar] [CrossRef] [PubMed]
- Islam, A.M.T.; Varol, M.; Habib, M.A.; Khan, R. Risk Assessment and Source Apportionment for Metals in Sediments of Kaptai Lake in Bangladesh Using Individual and Synergistic Indices and a Receptor Model. Mar. Pollut. Bull. 2023, 190, 114845. [Google Scholar] [CrossRef]
- Kurochkin, I.N.; Trifonova, T.A.; Kurbatov, Y.N. Heavy Metals in Soils of Various Functional Zones of Urbanized Territories: Assessment of the Content and Environmental Risk. Theor. Appl. Ecol. 2023, 2, 38–46. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. A review of comparative studies of spatial interpolation methods in environmental sciences: Performance and impact factors. Ecol. Inform. 2011, 6, 228–241. [Google Scholar] [CrossRef]
- Wu, J.; Norvell, W.A.; Welch, R.M. Kriging on highly skewed data for DTPA-extractable soil Zn with auxiliary information for pH and organic carbon. Geoderma 2006, 134, 187–199. [Google Scholar] [CrossRef]
- Xia, K.; Wu, T.X.; Zhang, S.W.; Wang, S.D.; Li, X.T.; Shen, Q.; Li, T. A New Method for High-Precision Estimation of Soil Organic Matter Using Two-Dimensional Correlation Spectroscopy to Support Collaborative Use of Global Open Soil Spectral Libraries. Geoderma 2024, 445, 116877. [Google Scholar] [CrossRef]
- Zhou, W.; Yang, H.; Xie, L.J.; Li, H.R.; Huang, L.; Zhao, Y.P. Hyperspectral Inversion of Soil Heavy Metals in Three-River Source Region Based on Random Forest Model. Catena 2021, 202, 105222. [Google Scholar] [CrossRef]
- Jordanova, D.; Goddu, S.R.; Kotsev, T.; Jordanova, N. Industrial Contamination of Alluvial Soils Near Fe-Pb Mining Site Revealed by Magnetic and Geochemical Studies. Geoderma 2013, 192, 237–248. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, Y.X.; Shang, K.; Ding, S.T.; Sun, W.C. Soil Cd Content Retrieval from Hyperspectral Remote Sensing Data Based on Organic Matter Characteristic Spectral Bands. Trans. Chin. Soc. Agric. Mach. 2024, 55, 186–195, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Abrantes, G.; Almeida, V.; Maia, A.J.; Nascimento, R.; Nascimento, C.; Silva, Y.; Silva, Y.; Veras, G. Comparison between Variable-Selection Algorithms in PLS Regression with Near-Infrared Spectroscopy to Predict Selected Metals in Soil. Molecules 2023, 28, 6959. [Google Scholar] [CrossRef]
- Wang, X.; An, S.; Xu, Y.Q.; Hou, H.P.; Chen, F.Y.; Yang, Y.J.; Zhang, S.; Liu, R. A Back Propagation Neural Network Model Optimized by Mind Evolutionary Algorithm for Estimating Cd, Cr, and Pb Concentrations in Soils Using Vis-NIR Diffuse Reflectance Spectroscopy. Appl. Sci. 2020, 10, 51. [Google Scholar] [CrossRef]
- Kaestner, F.; Sut-Lohmann, M.; Ramezany, S.; Raab, T.; Feilhauer, H.; Chabrillat, S. Estimating Heavy Metal Concentrations in Technosols with Reflectance Spectroscopy. Geoderma 2022, 406, 115512. [Google Scholar] [CrossRef]
- Cui, S.C.; Zhou, K.F.; Ding, R.F.; Cheng, Y.Y.; Jiang, G. Estimation of soil copper content based on fractional-order derivative spectroscopy and spectral characteristic band selection. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2022, 275, 121190. [Google Scholar] [CrossRef] [PubMed]
- Nawar, S.; Mohamed, E.S.; Sayed, S.E.E.; Mohamed, W.S.; Rebouh, N.Y.; Hammam, A.A. Estimation of Key Potentially Toxic Elements in Arid Agricultural Soils Using Vis-NIR Spectroscopy with Variable Selection and PLSR Algorithms. Front. Environ. Sci. 2023, 12, 1222871. [Google Scholar] [CrossRef]
- Tepanosyan, G.; Muradyan, V.; Tepanosyan, G.; Avetisyan, R.; Asmaryan, S.; Sahakyan, L.; Denk, M.; Glasser, C. Exploring Relationship of Soil PTE Geochemical and VIS-NIR Spectroscopy Patterns Near Cu-Mo Mine, Armenia. Environ. Pollut. 2023, 323, 121180. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.L.; Wang, Z.; Luo, Y.; Zhang, J.Q.; Tian, D.; Zhang, Y.D. Rapid Estimation of Soil Pb Concentration Based on Spectral Feature Screening and Multi-Strategy Spectral Fusion. Sensors 2023, 23, 7707. [Google Scholar] [CrossRef]
- Subi, X.; Eziz, M.; Zhong, Q.; Li, X.G. Estimating the Chromium Concentration of Farmland Soils in an Arid Zone from Hyperspectral Reflectance Using Partial Least Squares Regression Methods. Ecol. Indic. 2023, 161, 111987. [Google Scholar] [CrossRef]
- Azizi, K.; Ayoubi, S.; Nabiollahi, K.; Garosi, Y.; Gislum, R. Predicting Heavy Metal Contents by Applying Machine Learning Approaches and Environmental Covariates in West Iran. J. Geochem. Explor. 2022, 233, 106921. [Google Scholar] [CrossRef]
- Tasan, M.; Demir, Y.; Tasan, S.; Ozturk, E. Comparative Analysis of Different Machine Learning Algorithms for Predicting Trace Metal Concentrations in Soils Under Intensive Paddy Cultivation. Comput. Electron. Agric. 2024, 219, 108772. [Google Scholar] [CrossRef]
- Xu, X.B.; Ren, M.Y.; Gao, J.F.; Wu, Q.Y.; Liu, P.Y.; Lv, J.S. Spectroscopic diagnosis of zinc contaminated soils based on competitive adaptive reweighted sampling algorithm and an improved support vector machine. Spectrosc. Lett. 2020, 53, 86–99. [Google Scholar] [CrossRef]
- Mouazen, A.M.; Nyarko, F.; Qaswar, M.; Tóth, G.; Gobin, A.; Moshou, D. Spatiotemporal Prediction and Mapping of Heavy Metals at Regional Scale Using Regression Methods and Landsat 7. Remote Sens. 2021, 13, 4615. [Google Scholar] [CrossRef]
- Guo, H.Y.; Yang, K.; Wu, F.; Chen, Y.; Shen, J.X. Regional Inversion of Soil Heavy Metal Cr Content in Agricultural Land Using Zhuhai-1 Hyperspectral Images. Sensors 2023, 23, 8756. [Google Scholar] [CrossRef]
- Wang, Y.; Abliz, A.; Ma, H.B.; Liu, L.; Kurban, A.; Halik, Ü.; Pietikainen, M.; Wang, W. Hyperspectral Estimation of Soil Copper Concentration Based on Improved TabNet Model in the Eastern Junggar Coalfield. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5534020. [Google Scholar] [CrossRef]
- Sawut, R.; Kasim, N.; Abliz, A.; Li, H.; Yalkun, A.; Maihemuti, B. Investigation of Optimized Indices for Assessing Heavy Metal Levels in Soils Surrounding an Open Pit Coal Mine. Int. J. Appl. Earth Observ. Geoinf. 2018, 73, 14–25. [Google Scholar] [CrossRef]
- Lin, X.; Su, Y.C.; Shang, J.L.; Sha, J.M.; Li, X.M.; Sun, Y.Y. Hyperspectral Modeling of Soil Zinc Levels Using Geographically Weighted Regression: The Impact of Fractional-Order Differential. Remote Sens. 2019, 11, 636. [Google Scholar] [CrossRef]
- Vina, A.; Gitelson, A.A.; Nguy-Robertson, A.L.; Peng, Y. Comparative Analysis of Various Vegetation Indices for the Remote Evaluation of Green Leaf Area Index in Crops. Remote Sens. Environ. 2011, 115, 3468–3478. [Google Scholar] [CrossRef]
- Zhang, Z.P.; Ding, J.L.; Wang, J.Z.; Ge, X.Y.; Li, Z.S. Quantitative Assessment of Soil Organic Matter Content Using a Three-Dimensional Spectral Index: A Case Study in Ebinur Lake Basin, Xinjiang. Spectrosc. Spect. Anal. 2020, 40, 1514–1522. [Google Scholar] [CrossRef]
- Hong, Y.S.; Guo, L.; Chen, S.C.; Linderman, M.; Mouazen, A.M.; Yu, L.; Chen, Y.; Liu, Y.; Liu, Y.; Cheng, H.; et al. Evaluating the Capacity of Airborne Hyperspectral Imagery for Estimating Topsoil Organic Carbon: The Influence of Fractional-Order Derivative and Optimal Band Combination Algorithms. Geoderma 2020, 365, 114228. [Google Scholar] [CrossRef]
- Song, Y.X.; Ji, J.F.; Mao, C.P.; Ayoko, G.A.; Frost, R.L.; Yang, Z.; Yuan, X. Utilizing Visible-NIR Reflectance Spectroscopy to Predict Seasonal Variations of Trace Metals in Suspended Solids of the Yangtze River. Catena 2013, 109, 217–224. [Google Scholar] [CrossRef]
- Ge, X.Y.; Ding, J.L.; Jin, X.L.; Wang, J.Z.; Chen, X.Y.; Li, X.H.; Liu, J.; Xie, B. Estimating Soil Moisture Content in Agricultural Lands through UAV-Based Hyperspectral Imagery in Arid Regions. Remote Sens. 2021, 13, 1562. [Google Scholar] [CrossRef]
- Geng, J.; Lv, J.W.; Liao, C.H.; Tan, Q.Y.; Qang, T.X.; Fang, H.J.; Wang, L. Prediction of soil organic carbon in black soil based on a synergistic scheme from hyperspectral data: Combining fractional-order derivatives and three-dimensional spectral indices. Comput. Electron. Agric. 2024, 220, 108905. [Google Scholar] [CrossRef]
- Zhu, C.M.; Wang, H.W.; Xia, X.; Ma, L.G.; Tong, Y.J.; Quan, L.Z.R. Retrieval of Soil Organic Matter Content Based on Spectral Index and Machine Learning. Jiangsu Agric. Sci. 2020, 48, 233–241. (In Chinese) [Google Scholar] [CrossRef]
- Feng, Y.; Wang, J.L.; Tang, Y.L. Estimation and inversion of soil heavy metal arsenic (As) based on UAV hyperspectral platform. Microchem. J. 2024, 207, 112027. [Google Scholar] [CrossRef]
- Fu, P.J.; Yang, K.M.; Meng, F.; Zhang, W.; Cui, Y.; Feng, F.S.; Yao, G.B. A Novel Three-Band Spectral and Metal Element Index for Estimating Soil Arsenic Levels in Mining Areas. Process Saf. Environ. Prot. 2022, 157, 22–36. [Google Scholar] [CrossRef]
- Fu, C.B.; Xiong, H.G.; Tian, A.H. Investigating the Effect of Fractional Derivative on Hyperspectral Data for Soil Organic Matter Content in Arid Regions. J. Spectrosc. 2019, 2019, 7159317. [Google Scholar] [CrossRef]
- Hong, Y.S.; Chen, S.C.; Liu, Y.L.; Zhang, Y.; Yu, L.; Chen, Y.Y. Enhancement of Soil Organic Matter Estimation Accuracy via Combining Fractional Order Derivative Techniques and Memory-Based Learning Algorithms Using Visible and Near-Infrared Spectroscopy. Catena 2019, 174, 104–116. [Google Scholar] [CrossRef]
- Meng, C.; Hong, M.; Hu, Y.C.; Li, F. Assessment of Soil Copper Concentration in Mining Areas Using Optimized Spectral Indices and Machine Learning Algorithms. Sensors 2024, 16, 4153. [Google Scholar] [CrossRef]
- Demetriadesshah, T.H.; Steven, M.D.; Clark, J.A. High-Resolution Derivative Spectra in Remote Sensing Applications. Remote Sens. Environ. 1990, 33, 55–64. [Google Scholar] [CrossRef]
- Tsai, F.; Philpot, W. Analyzing Derivatives of Hyperspectral Data. Remote Sens. Environ. 1998, 66, 41–51. [Google Scholar] [CrossRef]
- Shi, T.Z.; Yang, C.; Liu, H.Z.; Wu, C.; Wang, Z.H.; Li, H.; Zhang, H.; Guo, L.; Wu, G.; Su, F. Mapping Lead Concentrations in Urban Topsoil Utilizing Proximal and Remote Sensing Techniques Coupled with Hybrid Statistical Approaches. Environ. Pollut. 2020, 272, 116041. [Google Scholar] [CrossRef]
- Hong, Y.S.; Shen, R.L.; Cheng, H.; Chen, Y.Y.; Zhang, Y.; Liu, Y.; Zhou, M.; Yu, L.; Liu, Y.; Liu, Y. Predicting Lead and Zinc Levels in Agricultural Soils in Peri-Urban Regions Using Reflectance Spectroscopy: The Role of Fractional-Order Derivative and Random Forest Techniques. Sci. Total Environ. 2019, 651, 1969–1982. [Google Scholar] [CrossRef] [PubMed]
- Hong, Y.S.; Liu, Y.L.; Chen, Y.Y.; Liu, Y.F.; Yu, L.; Liu, Y. Implementing Fractional-Order Derivative Methods for the Quantitative Estimation of Soil Organic Matter Content Using Visible and Near-Infrared Reflectance Spectroscopy. Geoderma 2019, 337, 758–769. [Google Scholar] [CrossRef]
- Bhadra, S.; Sagan, V.; Maimaitijiang, M.; Maimaitiyiming, M.; Newcomb, M.; Shakoor, N.; Mockler, T.C. Hyperspectral Data-Driven Estimation of Leaf Chlorophyll Concentration in Sorghum Using Derivative Calculus and Machine Learning Techniques. Remote Sens. 2020, 12, 2082. [Google Scholar] [CrossRef]
- Chen, L.H.; Lai, J.; Tan, K.; Wang, X.; Chen, Y.; Ding, J.W. A New Method for Estimating Soil Heavy Metals Based on Spectral Indices: Integrating Fractional-Order Derivative Pretreatment with Absorption Mechanism Understanding. Sci. Total Environ. 2022, 813, 151882. [Google Scholar] [CrossRef]
- Tang, R.N.; Li, X.W.; Li, C.; Jiang, K.X.; Hu, W.F.; Wu, J.J. Evaluating Total Nitrogen Content in Rubber Plantation Soil Utilizing Hyperspectral Data and Fractional Order Derivative Methods. Electronics 2022, 11, 1956. [Google Scholar] [CrossRef]
- Xiao, D.; Huang, J.; Li, J.; Fu, Y.H.; Li, Z.N. Inversion Analysis of Cadmium Content in Soil Using Reflection Spectroscopy Coupled with MSC-ELM Model. Spectrochim. Acta A 2022, 283, 121696. [Google Scholar] [CrossRef]
- Fu, C.B.; Gan, S.; Xiong, H.G.; Tian, A.H. An Innovative Method for Estimating Soil Organic Matter via a Combination Model Incorporating Short Memory Fractional Order Derivative and Machine Learning Techniques. Infrared Phys. Technol. 2023, 134, 104922. [Google Scholar] [CrossRef]
- Liu, Y.; Lu, Y.Y.; Chen, D.Y.; Zheng, W.; Ma, Y.X.; Pan, X.Z. Simultaneously Estimating Diverse Soil Properties Under Moist Conditions Using Fractional-Order Derivative of Vis-NIR Spectra Coupled with Deep Learning Approaches. Geoderma 2023, 438, 116653. [Google Scholar] [CrossRef]
- Song, G.M.; Wang, Q.; Jin, J. Enhancing Partial Least Squares Regression Estimation of Photosynthetic Capacity Using Fractional-Order Derivative Spectral Transformations from Hyperspectral Data. IEEE Trans. Geosci. Remote 2023, 61, 5510110. [Google Scholar] [CrossRef]
- Galvão, R.K.H.; Araújo, M.C.U.; Fragoso, W.D.; Silva, E.C.; José, G.E.; Soares, S.F.C. A Variable Elimination Approach to Enhance the Parsimony of MLR Models via the Successive Projections Algorithm. Chemom. Intell. Lab. 2008, 92, 83–91. [Google Scholar] [CrossRef]
- Vohland, M.; Ludwig, M.; Thiele-Bruhn, S.; Ludwig, B. Assessing Soil Properties through Visible to Near- and Mid-Infrared Spectroscopy: The Impact of Spectral Variable Selection Methods. Geoderma 2014, 223, 88–96. [Google Scholar] [CrossRef]
- Zhang, X.L.; Xue, J.; Xiao, Y.; Shi, Z.; Chen, S.C. Optimizing Variable Selection Methods for Predicting Soil Properties through a Regional Soil Vis-NIR Spectral Library. Remote Sens. 2023, 15, 465. [Google Scholar] [CrossRef]
- Wang, X.P.; Zhang, F.; Kung, H.T.; Johnson, V.C. Innovative Approaches for Enhancing Remote Sensing Estimates of Soil Organic Matter Content in the Ebinur Lake Wetland National Nature Reserve, Northwest China. Remote Sens. Environ. 2018, 218, 104–118. [Google Scholar] [CrossRef]
- Kahaer, Y.; Sawut, R.; Kasim, N.; Tashpolati, N.; Zhang, F.; Abliz, A. Estimation of Heavy Metal Levels in Soil Near Open Pit Coal Mines Utilizing Optimized Spectral Indices. Spectrosc. Spect. Anal. 2019, 39, 2486–2494. [Google Scholar] [CrossRef]
- Xia, K.; Xia, S.S.; Shen, Q.; Zhang, S.W.; Li, C.; Cheng, Q.; Zhou, J. Optimizing a Soil Particle Content Prediction Model Based on Combined Spectral Indices and the Successive Projections Algorithm Using Vis-NIR Spectroscopy. Spectroscopy 2021, 35, 24–34. [Google Scholar]
- Fu, P.J.; Zhang, J.W.; Yuan, Z.X.; Feng, J.F.; Zhang, Y.X.; Meng, F. Estimating Heavy Metal Levels in Entisols from a Mining Area Using Enhanced Spectral Indices and CatBoost. Sensors 2024, 24, 1492. [Google Scholar] [CrossRef] [PubMed]



| Three-Band Spectral Index | Calculation Formula |
|---|---|
| TBSI1 | |
| TBSI2 | |
| TBSI3 | |
| TBSI4 | |
| TBSI5 |
| Spectral Index Calculation Method | Spectral Band Position (nm) | Derivative Order | Determination Coefficient R2 | p Value |
|---|---|---|---|---|
| TBSI1 | 768.904, 426.696, 974.245 | 0.35 | 0.55 | <0.001 |
| TBSI2 | 768.904, 632.170, 922.910 | 0.55 | 0.52 | <0.001 |
| TBSI3 | 426.696, 512.275, 974.245 | 0.35 | 0.54 | <0.001 |
| TBSI3 | 443.812, 786.016, 460.927 | 1.15 | 0.54 | <0.001 |
| TBSI4 | 443.812,786.016, 460.927 | 1.15 | 0.46 | <0.001 |
| TBSI5 | 632.170, 922.910, 768.904 | 0.45 | 0.53 | <0.001 |
| Three-Band Spectral Index | Training Set | Testing Set | |||
|---|---|---|---|---|---|
| R2 | Fitting Relationship Formula | R2 | RMSE (mg·kg−1) | RPD | |
| TBSI1 (768.904, 426.696, 974.245, 0.35 order) | 0.55 | Y = 39.188X − 270.69 | 0.46 | 32.96 | 1.36 |
| TBSI2 (768.904, 632.170, 922.910, 0.55 order) | 0.52 | Y = 200.12X − 136.38 | 0.28 | 37.42 | 1.19 |
| TBSI3 (426.696, 512.275, 974.245, 0.35 order) | 0.54 | Y = 289.7 − 4746.7X | 0.51 | 30.90 | 1.46 |
| TBSI3 (443.812, 786.016, 460.927, 1.15 order) | 0.54 | Y = 8229.3X + 355.17 | 0.46 | 32.41 | 1.39 |
| TBSI4 (443.812,786.016, 460.927, 1.15 order)) | 0.46 | Y = 138.53 − 10,000,000X | 0.42 | 36.42 | 1.23 |
| TBSI5 (632.170, 922.910, 768.904, 0.45 order) | 0.53 | Y = 21.276X − 63.278 | 0.25 | 38.21 | 1.17 |
| Newly Constructed Spectral Index | Training Set | Testing Set | ||
|---|---|---|---|---|
| R2 | R2 | RMSE (mg·kg−1) | RPD | |
| TBSI1 [TBSI5 (632.170, 922.910, 768.904, 0.45 order), TBSI2 (768.904, 632.170, 922.910, 0.55 order), TBSI3 (426.696, 512.275, 974.245, 0.35 order)] | 0.65 | 0.56 | 29.40 | 1.52 |
| TBSI2 [TBSI2 (768.904, 632.170, 922.910, 0.55 order), TBSI4 (443.812,786.016, 460.927, 1.15 order)), TBSI3 (426.696, 512.275, 974.245, 0.35 order)] | 0.63 | 0.53 | 30.5 | 1.46 |
| TBSI3 [TBSI1 (768.904, 426.696, 974.245, 0.35 order), TBSI2 (768.904, 632.170, 922.910, 0.55 order), TBSI5 (632.170, 922.910, 768.904, 0.45 order)] | 0.59 | 0.38 | 34.86 | 1.28 |
| TBSI4 [TBSI1 (768.904, 426.696, 974.245, 0.35 order), TBSI2 (768.904, 632.170, 922.910, 0.55 order), TBSI5 (632.170, 922.910, 768.904, 0.45 order)] | 0.55 | 0.29 | 37.08 | 1.20 |
| TBSI5 [TBSI2 (768.904, 632.170, 922.910, 0.55 order),TBSI3 (426.696, 512.275, 974.245, 0.35 order), TBSI3 (443.812, 786.016, 460.927, 1.15 order)] | 0.60 | 0.49 | 31.63 | 1.41 |
| Spectral Index Form | R2 Maximum Value |
|---|---|
| Two-band: ratio spectral index | 0.44 |
| Two-band: difference spectral index | 0.47 |
| Two-band: normalized spectral index | 0.45 |
| Three-band: TBSI1 | 0.55 |
| Three-band: TBSI2 | 0.52 |
| Three-band: TBSI3 | 0.54 |
| Three-band: TBSI4 | 0.46 |
| Three-band: TBSI5 | 0.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, S.; Jiang, G.; Lu, J. Rapid Estimation of Soil Copper Content Using a Novel Fractional Derivative Three-Band Index and Spaceborne Hyperspectral Data. Fractal Fract. 2025, 9, 523. https://doi.org/10.3390/fractalfract9080523
Cui S, Jiang G, Lu J. Rapid Estimation of Soil Copper Content Using a Novel Fractional Derivative Three-Band Index and Spaceborne Hyperspectral Data. Fractal and Fractional. 2025; 9(8):523. https://doi.org/10.3390/fractalfract9080523
Chicago/Turabian StyleCui, Shichao, Guo Jiang, and Jiawei Lu. 2025. "Rapid Estimation of Soil Copper Content Using a Novel Fractional Derivative Three-Band Index and Spaceborne Hyperspectral Data" Fractal and Fractional 9, no. 8: 523. https://doi.org/10.3390/fractalfract9080523
APA StyleCui, S., Jiang, G., & Lu, J. (2025). Rapid Estimation of Soil Copper Content Using a Novel Fractional Derivative Three-Band Index and Spaceborne Hyperspectral Data. Fractal and Fractional, 9(8), 523. https://doi.org/10.3390/fractalfract9080523







