Fractional Wave Structures in a Higher-Order Nonlinear Schrödinger Equation with Cubic–Quintic Nonlinearity and β-Fractional Dispersion

Abstract

This study employs the improved modified extended tanh method (IMETM) to derive exact analytical solutions of a higher-order nonlinear Schrödinger (HNLS) model, incorporating $\beta$-fractional derivatives in both time and space. Unlike classical methods such as the inverse scattering transform or Hirota’s bilinear technique, which are typically limited to integrable systems and integer-order operators, the IMETM offers enhanced flexibility for handling fractional models and higher-order nonlinearities. It enables the systematic construction of diverse solution types—including Weierstrass elliptic, exponential, Jacobi elliptic, and bright solitons—within a unified algebraic framework. The inclusion of fractional derivatives introduces richer dynamical behavior, capturing nonlocal dispersion and temporal memory effects. Visual simulations illustrate how fractional parameters $\alpha$ (space) and $\beta$ (time) affect wave structures, revealing their impact on solution shape and stability. The proposed framework provides new insights into fractional NLS dynamics with potential applications in optical fiber communications, nonlinear optics, and related physical systems.

1. Introduction

Nonlinear partial differential equations (NLPDEs) are applied across a wide range of disciplines, including fluid dynamics, cosmology, hydrodynamics, plasma physics, biology, and optics, to model various complex physical phenomena [1,2,3,4,5]. Obtaining exact solutions to these NLPDEs is essential for comprehending the behavior of such intricate processes. Recently, several integration methods have been developed to find these exact solutions. These methods include the extended Bernoulli’s equation technique [6], the Jacobi elliptic function method, Kudryashov’s method [7], the Hirota bilinear approach [8], and the F-expansion technique [9]. These advanced techniques provide powerful tools for solving NLPDEs, facilitating deeper insights into the underlying mechanics of the modeled phenomena [10].

Advancements in the telecommunications sector heavily rely on the understanding of wave propagation in optical fibers. To model this phenomenon, researchers often employ a diverse array of NLPDEs, each providing unique insights into the underlying dynamics. The nonlinear Schrödinger (NLS) model is a cornerstone for describing wave packet evolution in optical fibers, capturing the interplay between group velocity dispersion and Kerr nonlinearity. Zayed et al. [11] derived exact solutions for the NLS equation with anti-cubic nonlinearity and Hamiltonian perturbations, providing insights into soliton stability under non-standard nonlinear effects. Zhang et al. [12] obtained exact traveling wave solutions for two NLS variants, enhancing the analytical framework for pulse propagation. Soliman et al. [13] extended the NLS model to include spatial fractional derivatives, demonstrating their impact on soliton dynamics in optical fibers. Ali et al. [14] explored optical soliton solutions of a generalized perturbed nonlinear Schrödinger equation under a dual-power law nonlinearity, providing insights into pulse propagation in complex nonlinear media. Samir et al. [15] analyzed traveling and soliton wave dynamics in the extended (3+1)-dimensional Kadomtsev–Petviashvili equation, shedding light on fluid flow phenomena described by higher-dimensional nonlinear PDEs. Some of these studies collectively underscore the NLS model’s versatility in modeling complex nonlinear dynamics in optical fibers, motivating our focus on its fractional extension with cubic–quintic interactions. The Biswas–Arshed model [16,17], on the other hand, extends the NLS equation by incorporating higher-order nonlinear effects, enabling a more comprehensive representation of the optical fiber dynamics.

The Fokas–Lenells equation [18,19], derived from the perspective of inverse scattering theory, provides a generalized framework for analyzing soliton solutions and their interactions in optical fibers. Similarly, the Chen–Lee–Liu equation [20,21] and the Kundu–Mukherjee–Naskar [22,23] model offer alternative formulations that account for additional physical phenomena, such as fourth-order dispersion and variable coefficients, respectively.

The Radhakrishnan–Kundu–Lakshmanan equation (RKL) [24,25] is another prominent model that has been extensively studied in the context of optical fiber communications. It incorporates the effects of self-phase modulation, group velocity dispersion, and stimulated Raman scattering, making it a versatile tool for understanding the complex dynamics of wave propagation in optical fibers.

These NLPDEs serve as fundamental tools for understanding various aspects of wave behavior in optical fibers, which is crucial for improving signal transmission efficiency and minimizing losses. By applying these models, researchers can develop more effective methods for managing dispersion and nonlinearity, leading to the design of more robust and higher-capacity telecommunication networks.

Beyond the telecommunications realm, nonlinear Schrödinger equations (NLSEs) also hold pivotal importance in quantum mechanics and fluid dynamics as they are instrumental in capturing the wave dynamics in optical fibers and photonics. Notably, the incorporation of a fractional beta derivative into these equations introduces an additional layer of complexity, enabling a more accurate representation of the anomalous dispersion effects observed in practical applications. This paper focuses on the analysis of the fractional beta derivative Schrödinger equation, as described in [26].

$$\begin{array}{ccc}\hfill & & {\displaystyle \frac{D_{xx}^{\alpha }u}{2}}+i{D}_t^{\beta }u+u{\left|u\right|}^2-i\sigma \left(D_{xxx}^{\alpha }u+6D_x^{\alpha }u{\left|u\right|}^2\right)+\hfill \\ & & \gamma \left(D_{xxxx}^{\alpha }u+6u^{*}\left|D_x^{\alpha }{u|}^2+4u\right|D_x^{\alpha }{u|}^2+8{\left(D_{xx}^{\alpha }u\right)}^{*}{\left|u\right|}^2+2u^2{\left(D_{xx}^{\alpha }u\right)}^{*}+6u{\left|u\right|}^4\right)=0.\hfill \end{array}$$

(1)

In this equation, $u=u(x,t)$ describes the complex-valued field that depends on the spatial variable x, as well as the time variable t. $D_{xx}^{\alpha }u$ represents the dispersion effects in the optical fiber, while $\alpha$ is the order of the fractional derivative capturing anomalous dispersion. $D_t^{\beta }u$ represents the temporal evolution of the optical field u, with $\beta$ being the order of the fractional time derivative. ${u\left|u\right|}^2$ is a nonlinear term that represents the Kerr nonlinearity in the optical fiber The other terms represent additional dispersive effects, such as third-order dispersion, as well as nonlinear effects like self-steepening, with $\sigma$ as the coefficient. $\alpha$ and $\beta$ are the orders of the fractional derivative and have values between 0 and 1. The $\beta$ derivative, a generalization of the classical derivative, is defined as follows [27,28,29]:

$$D^{\beta }f\left(t\right)=\underset{\delta \to 0}{lim}{\displaystyle \frac{f(t+\delta {(t+\frac{1}{\Gamma \left(\beta \right)})}^{1-\beta })-f\left(t\right)}{\delta }},t>0,0<\beta \le 1.$$

(2)

We acknowledge that several generalized fractional operators based on Mittag–Leffler memory kernels were introduced well before the Atangana–Baleanu class. Key foundational contributions include the works of Viñales [30], Desposito [31], Sandev [32,33,34], Tomovski [35,36], and others [37], whose formulations encompass and extend various operator families used today. The fractional derivatives capture the non-Gaussian and non-Markovian nature of the dispersion and nonlinear processes, allowing for a more accurate description of pulse propagation in realistic fiber-optic systems. The fractional Schrödinger equation has been extensively studied in the field of fiber optics to model the propagation of optical waves, particularly for ultrashort pulse propagation. The inclusion of fractional derivatives allows for a more accurate representation of the anomalous dispersion and nonlinear effects that arise in optical fibers. One of the pioneering works in this area is the paper by Magin et al. [38], which derived a generalized fractional Schrödinger equation to describe pulse propagation in nonlinear optical fibers. The authors showed that the fractional derivatives can capture the non-Gaussian and non-Markovian nature of the dispersion and nonlinear processes, leading to a more realistic model compared to the standard nonlinear Schrödinger equation. Building upon this foundation, Bhattacharya et al. [39] investigated the soliton solutions of the fractional Schrödinger equation and their stability in the context of fiber optics. They demonstrated that the fractional order of the derivatives significantly impacts the soliton dynamics and propagation characteristics. More recently, Keshavarz and Soori [40] studied the numerical simulation of the fractional Schrödinger equation for fiber-optic communication systems. They proposed efficient numerical methods to solve the equation and analyzed the effects of the fractional orders on the pulse propagation and distortion. Additionally, Coskun et al. [41] explored the use of the fractional Schrödinger equation to model the impact of nonlinear effects, such as four-wave mixing and self-phase modulation, on the performance of wavelength-division multiplexed fiber-optic communication systems.

While many analytical methods have been applied to classical and fractional models, there remains a clear need for exact solutions to higher-order NLS systems incorporating both space and time fractional derivatives. These models are increasingly important for capturing the memory and nonlocal dispersion effects present in ultrafast optical fibers, nonlinear media, and quantum transport systems. In this work, we address this gap by applying the IMETM to a higher-order nonlinear Schrödinger equation involving $\alpha$- and $\beta$-fractional derivatives, cubic–quintic nonlinearity, and higher-order dispersion. The IMETM enables the derivation of diverse exact solutions—ranging from bright solitons to elliptic and exponential forms—along with a detailed analysis of the influence of fractional parameters on wave profiles. The main goals of this study are as follows:

• To derive exact analytical solutions to a generalized fractional HNLS model using the IMETM;
• To examine how fractional orders $\alpha$ (space) and $\beta$ (time) shape wave propagation dynamics;
• To provide physically meaningful simulations that capture soliton behavior under fractional dispersion.

These contributions offer both analytical insight and practical relevance for the design and analysis of next-generation nonlinear wave systems.

This study is structured in the following way: Section 2 provides a brief overview of the proposed methodology. In Section 3, the method is applied to obtain precise solutions for the model under investigation. Section 4 includes graphical illustrations of some of these solutions to demonstrate the features of the propagating wave. The concluding section wraps up the work in Section 5. Some future work recommendations are presented in Section 6.

2. The Proposed Scheme

This section provides a brief discussion of the IMETM [42,43,44,45].

Let us consider a general form of an NLPDE, where V is a nonlinear operator (or function) acting on the dependent variable f and its various fractional derivatives with respect to time and space:

$$V(f,D_t^{\alpha }f,D_x^{\alpha }f,D_{xx}^{\alpha }f,\dots )=0.$$

(3)

The following steps need to be completed in order to apply the recommended technique to Equation (3).

Step (1): 

Equation (3) is converted to an ordinary differential equation (ODE) by applying the following wave transformation:

$$f(x,t)=M\left(z\right)e^{i\varphi },z={\displaystyle \frac{h{\left(\frac{1}{\Gamma \left(\alpha \right)}+x\right)}^{\alpha }}{\alpha }}-{\displaystyle \frac{\nu {\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }}{\beta }},\varphi =\theta -{\displaystyle \frac{k{\left(\frac{1}{\Gamma \left(\alpha \right)}+x\right)}^{\alpha }}{\alpha }}+{\displaystyle \frac{\omega {\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }}{\beta }}.$$

(4)

In this case, k denotes the wave’s speed. Afterwards, the Equation (3) becomes

$$H(M,M^{\prime },M^{″},M^{‴},M^{\left(4\right)},\dots )=0.$$

(5)

Step (2): 

Write the converted ODE’s solution as

$$M\left(z\right)=\sum _{j=0}^N{a}_j{{\rm Y}}^j\left(z\right)+\sum _{j=-1}^{-N}{b}_{-j}{{\rm Y}}^j\left(z\right),$$

(6)

where the following DE is satisfied by ${\rm Y}\left(z\right)$:

$${{\rm Y}}^{\prime }\left(z\right)=\sqrt{d_0+d_1{\rm Y}\left(z\right)+d_2{{\rm Y}}^2\left(z\right)+d_3{{\rm Y}}^3\left(z\right)+d_4{{\rm Y}}^4\left(z\right)}.$$

(7)

Step (3): 

The balancing rule is used to calculate the parameter N.

Step (4): 

Equations (6) and (5) are substituted into Equation (5) to produce a set of nonlinear algebraic equations, after which, the coefficients of ${{\rm Y}}^p\left(z\right)$ are gathered.

Step (5): 

The created system in step 4 is solved using Mathematica software packages V.13.3 to yield $a_j$ and $b_j$ and the parameters h, k, $\omega$, and $\nu$.

Step (6): 

Finally, by assigning distinct numerical values to the parameters $d_0$, $d_1$, $d_2$, $d_3$, and $d_4$, various solutions can be derived.

Case 1: 

$d_0=d_1=d_3=0$

$${\rm Y}\left(z\right)=\sqrt{-{\displaystyle \frac{d_2}{d_4}}}\mathrm{sech}\left(\sqrt{d_2}z\right),d_2>0,d_4<0.$$

Case 2: 

$d_1=d_3=0$

$${\rm Y}\left(z\right)=\sqrt{{\displaystyle \frac{-d_2{m}^2}{d_4(2m^2-1)}}}\mathrm{cn}\left(\sqrt{{\displaystyle \frac{d_2}{(2m^2-1)}}}z\right),d_2>0,d_4<0,d_0={\displaystyle \frac{d_2^2{m}^2(1-m^2)}{d_4{(2m^2-1)}^2}},$$

$${\rm Y}\left(z\right)=\sqrt{-{\displaystyle \frac{m^2}{d_4(2-m^2)}}}\mathrm{dn}\left(\sqrt{{\displaystyle \frac{d_2}{(2-m^2)}}}z\right),d_2>0,d_4<0,d_0={\displaystyle \frac{d_2^2(1-m^2)}{d_4{(2-m^2)}^2}},$$

Case 3: 

$d_2=d_4=0,d_3>0$

$${\rm Y}\left(z\right)=\wp \left({\displaystyle \frac{\sqrt{d_3}}{2}}z,{\displaystyle \frac{-4d_1}{d_3}},{\displaystyle \frac{-4d_0}{d_3}}\right),.$$

Case 4: 

$d_0=d_1=d_2=0$

$${\rm Y}\left(z\right)={\displaystyle \frac{d_3}{2d_4}}exp\left({\displaystyle \frac{d_3}{2\sqrt{-d_4}}}z\right).$$

Step (7): 

To obtain solutions for Equation (3), add the constants $a_j$ and $b_{-j}$ to Equation (5) in addition to the described general solutions of Equation (6). To elucidate the rationale for selecting the IMETM, it is instructive to compare it with other established analytical techniques, such as Hirota’s bilinear method and the inverse scattering transform (IST). Hirota’s method excels in deriving multi-soliton solutions for integrable NLPDEs by transforming them into bilinear forms, but its applicability is often limited to soliton solutions and integrable systems, which may not fully accommodate the non-local nature of $\beta$-fractional derivatives in the fractional NLSE. Similarly, the IST provides a rigorous framework for integrable systems, yielding soliton solutions through scattering analysis, yet its computational intensity and complexity make it less practical for non-integrable or fractional systems. In contrast, the IMETM offers distinct strengths: its versatility in generating diverse solution types, including solitons, Jacobi elliptic, Weierstrass elliptic, and exponential functions, enables a broader exploration of the fractional NLSE’s dynamics. Additionally, the IMETM’s straightforward algebraic approach, which reduces the NLPDE to a system of nonlinear equations solvable via software like Mathematica, enhances computational efficiency and accessibility. Its seamless incorporation of fractional derivatives through wave transformation further optimizes its suitability for modeling complex, non-Gaussian wave phenomena, making the IMETM a robust and flexible tool for this study. Despite its strengths, the IMETM has certain limitations. It relies on a predefined functional ansatz—typically involving hyperbolic or elliptic functions—which restricts the class of solutions to those compatible with this structure. As a result, the method may not capture more complex or irregular solution behaviors such as rogue waves, chaotic waveforms, or multi-soliton interactions. Additionally, while the method is well-suited for generating analytical solutions, it is not inherently designed for exploring solution stability or performing long-time dynamics, which may require complementary numerical methods. These constraints should be considered when applying the IMETM to broader classes of fractional nonlinear systems.

3. Applying to the Studied Model

The aim of this section is to derive exact solutions for Equation (1) in the following manner:

$$\begin{array}{c}\hfill u(x,t)=Q\left(z\right)e^{i\varphi },z={\displaystyle \frac{h{\left(\frac{1}{\Gamma \left(\alpha \right)}+x\right)}^{\alpha }}{\alpha }}-{\displaystyle \frac{\nu {\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }}{\beta }}\mathbf{and}\varphi =\theta -{\displaystyle \frac{k{\left(\frac{1}{\Gamma \left(\alpha \right)}+x\right)}^{\alpha }}{\alpha }}+{\displaystyle \frac{\omega {\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }}{\beta }}.\end{array}$$

(8)

By using Equation (8) as a substitute for Equation (1), the fractional derivative NLPDE can be transformed into the entire complex derivative ODE. The generated ODE’s real and imaginary portions are, as follows, in that order:

$$\begin{array}{ccc}\hfill & & 2\gamma h^4{Q}^{\left(4\right)}\left(z\right)+h^2\left(-12\gamma k^2-6k\sigma +1\right)Q^{″}\left(z\right)+Q\left(z\right)\left(20\gamma h^2{Q}^{\prime }{\left(z\right)}^2+2\gamma k^4+2k^3\sigma -k^2-2\omega \right)+\hfill \\ & & 20\gamma h^{2}Q{\left(z\right)}^2{Q}^{″}\left(z\right)-2Q{\left(z\right)}^3\left(12\gamma k^2+6k\sigma -1\right)+12\gamma Q{\left(z\right)}^5=0,\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill & & 2Q^{\prime }\left(z\right)\left(hk\left(4\gamma k^2+3k\sigma -1\right)-6hQ{\left(z\right)}^2(4\gamma k+\sigma )-\nu \right)-2h^3{Q}^{\left(3\right)}\left(z\right)(4\gamma k+\sigma )=0.\hfill \end{array}$$

(10)

Equating the coefficients in Equation (10) to zero yields

$$\begin{array}{ccc}& & k=-{\displaystyle \frac{\sigma }{4\gamma }},\hfill \\ & & \nu =hk\left(4\gamma k^2+3k\sigma -1\right).\hfill \end{array}$$

To implement the recommended method, the integer N must be calculated. We balance $Q^{\left(4\right)}$ with $Q^{″}{Q}^2$ to obtain $N=1$. The following can then be used to express the solution to the resulting ordinary differential equation (ODE):

$$Q\left(z\right)=s_0+s_1{\rm Y}\left(z\right)+{\displaystyle \frac{r_1}{{\rm Y}\left(z\right)}}.$$

(11)

The system of nonlinear algebraic equations is derived by substituting Equation (11) and Equation (6) into Equation (9) and equating the coefficients of ${\rm Y}\left(z\right)$ to zero. Using Mathematica software, this system can be solved to obtain the results for Equation (1).

Case 1. $d_0=d_1=d_3=0$

$$\begin{array}{ccc}& & s_0=0,\hfill \\ & & s_1=\sqrt{-d_4}h,\hfill \\ & & s_2=0,\hfill \\ & & \omega ={\displaystyle \frac{-8\gamma {\sigma }^2+256{\gamma }^4{d}_2^2{h}^4+128{\gamma }^3{d}_2{h}^2+96{\gamma }^2{d}_2{h}^2{\sigma }^2-3{\sigma }^4}{256{\gamma }^3}}.\hfill \end{array}$$

As a result, for Equation (1), it is feasible to supply a bright soliton solution:

$$\begin{array}{cc}\hfill u(x,t)=& h\sqrt{d_2}\mathrm{Sec}\mathrm{h}\left[\sqrt{d_2}\left({\displaystyle \frac{h\sigma \left(-\frac{{\sigma }^2}{2\gamma }-1\right){\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }}{4\beta \gamma }}+{\displaystyle \frac{h{\left(\frac{1}{\Gamma \left(\alpha \right)}+x\right)}^{\alpha }}{\alpha }}\right)\right].\hfill \\ \hfill & \times exp\left(i\left(\theta -{\displaystyle \frac{k{\left(\frac{1}{\Gamma \left(\alpha \right)}+x\right)}^{\alpha }}{\alpha }}+{\displaystyle \frac{\omega {\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }}{\beta }}\right)\right).\hfill \end{array}$$

(12)

Case 2. $d_1=d_3=0,d_0={\displaystyle \frac{d_2^{2}P}{d_4}}$, where, as mentioned in case 2 previously, P is altered in accordance with the Jacobi function type

$$\begin{array}{ccc}& & s_0=0,\hfill \\ & & s_1=\sqrt{-d_4}h,\hfill \\ & & s_2=0,\hfill \\ & & \omega ={\displaystyle \frac{-8\gamma {\sigma }^2+256{\gamma }^4{d}_2^2{h}^4+512{\gamma }^4{d}_2^2{h}^{4}p+128{\gamma }^3{d}_2{h}^2+96{\gamma }^2{d}_2{h}^2{\sigma }^2-3{\sigma }^4}{256{\gamma }^3}}.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill u(x,t)& =& h\sqrt{{\displaystyle \frac{m^2}{2-m^2}}}\mathrm{dn}\left(\left.\left({\displaystyle \frac{h{\left(x+\frac{1}{\Gamma \left(\alpha \right)}\right)}^{\alpha }}{\alpha }}-{\displaystyle \frac{\nu {\left(t+\frac{1}{\Gamma \left(\beta \right)}\right)}^{\beta }}{\beta }}\right)\sqrt{{\displaystyle \frac{d_2}{2-m^2}}}\right|m\right)\hfill \\ & & \times exp\left(i\left(\theta -{\displaystyle \frac{k{\left(\frac{1}{\Gamma \left(\alpha \right)}+x\right)}^{\alpha }}{\alpha }}+{\displaystyle \frac{\omega {\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }}{\beta }}\right)\right),\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill u(x,t)& =& h\sqrt{{\displaystyle \frac{d_2{m}^2}{2m^2-1}}}\mathrm{cn}\left(\left.\left({\displaystyle \frac{h{\left(x+\frac{1}{\Gamma \left(\alpha \right)}\right)}^{\alpha }}{\alpha }}-{\displaystyle \frac{\nu {\left(t+\frac{1}{\Gamma \left(\beta \right)}\right)}^{\beta }}{\beta }}\right)\sqrt{{\displaystyle \frac{d_2}{2m^2-1}}}\right|m\right)\hfill \\ & & \times exp\left(i\left(\theta -{\displaystyle \frac{k{\left(\frac{1}{\Gamma \left(\alpha \right)}+x\right)}^{\alpha }}{\alpha }}+{\displaystyle \frac{\omega {\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }}{\beta }}\right)\right).\hfill \end{array}$$

(14)

Case 3. $d_2=d_4=0,d_3>0$

$$\begin{array}{ccc}& & s_1=0,\hfill \\ & & s_2=\sqrt{-d_0}h,\hfill \\ & & \omega ={\displaystyle \frac{-8\gamma {\sigma }^2-3{\sigma }^4+11776{\gamma }^4{s}_0^4+768{\gamma }^3{s}_0^2+576{\gamma }^2{s}_0^2{\sigma }^2}{256{\gamma }^3}},\hfill \\ & & d_1=-{\displaystyle \frac{4\sqrt{-d_0}{s}_0}{h}},\hfill \\ & & d_3={\displaystyle \frac{8s_0^3}{\sqrt{-d_0}{h}^3}}.\hfill \end{array}$$

Next, we can provide a Weierstrass elliptic solution

$$\begin{array}{ccc}\hfill u(x,t)& =& {\displaystyle \frac{\sqrt{-d_0}h}{\wp \left(\sqrt{2}\left(\frac{h{\left(x+\frac{1}{\Gamma \left(\alpha \right)}\right)}^{\alpha }}{\alpha }-\frac{\nu {\left(t+\frac{1}{\Gamma \left(\beta \right)}\right)}^{\beta }}{\beta }\right)\sqrt{\frac{s_0^3}{h^3\sqrt{-d_0}}};-\frac{2h^2{d}_0}{s_0^2},-\frac{h^3\sqrt{-d_0}{d}_0}{2s_0^3}\right)}}+s_0\hfill \\ & & \times exp\left(i\left(\theta -{\displaystyle \frac{k{\left(\frac{1}{\Gamma \left(\alpha \right)}+x\right)}^{\alpha }}{\alpha }}+{\displaystyle \frac{\omega {\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }}{\beta }}\right)\right).\hfill \end{array}$$

(15)

Case 4. $d_3=d_4=0,d_0={\displaystyle \frac{d_1^2}{4d_2}}$

$$\begin{array}{ccc}& & s_0={\displaystyle \frac{\sqrt{-4\gamma -3{\sigma }^2}}{4\sqrt{3}\gamma }},\hfill \\ & & s_1=-{\displaystyle \frac{\sqrt{3}\gamma d_3{h}^2}{\sqrt{-4\gamma -3{\sigma }^2}}},\hfill \\ & & s_2=0,\hfill \\ & & \omega ={\displaystyle \frac{-32{\gamma }^2-72\gamma {\sigma }^2-27{\sigma }^4}{768{\gamma }^3}},\hfill \\ & & d_4={\displaystyle \frac{3{\gamma }^2{d}_3^2{h}^2}{4\gamma +3{\sigma }^2}}.\hfill \end{array}$$

Next, we are able to provide an exponential solution for (1):

$$\begin{array}{ccc}\hfill u(x,t)& =& ({\displaystyle \frac{\sqrt{-4\gamma -3{\sigma }^2}}{4\sqrt{3}\gamma }}-{\displaystyle \frac{\left(4\gamma +3{\sigma }^2\right)exp\left(\frac{d_3\left(\frac{h{\left(\frac{1}{\Gamma \left(\alpha \right)}+x\right)}^{\alpha }}{\alpha }-\frac{\nu {\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }}{\beta }\right)}{2\sqrt{3}\sqrt{-\frac{{\gamma }^2{d}_3^2{h}^2}{4\gamma +3{\sigma }^2}}}\right)}{2\sqrt{3}\gamma \sqrt{-4\gamma -3{\sigma }^2}}})\hfill \\ & & \times exp\left(i\left(\theta -{\displaystyle \frac{k{\left(\frac{1}{\Gamma \left(\alpha \right)}+x\right)}^{\alpha }}{\alpha }}+{\displaystyle \frac{\omega {\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }}{\beta }}\right)\right).\hfill \end{array}$$

(16)

4. Graphical Simulations of Some Obtained Solutions

To illustrate the characteristics of the acquired outcomes, the selected solutions are shown as graphical simulations. The bright soliton of Equation (12) with $\sigma =2.95,\gamma =-1.6,\alpha =1,h=0.66,d_2=5.44$ is visually simulated in Figure 1. Bright soliton profiles corresponding to Equation (12) for fixed spatial fractional order $\alpha =1$ and varying temporal orders $\beta =0.55$, $0.7$, and 1 is shown graphically. The horizontal axis represents space x (arbitrary units), and the vertical axis denotes the optical field magnitude $\left|u\right(x,t\left)\right|$. As $\beta$ increases, the soliton becomes narrower and more localized, indicating reduced temporal memory effects. The same parameter values are used in Figure 2, but with the difference that $\beta$ = 1 and various values of $\alpha$ are used to show the effect of the fractional derivative on space. Bright soliton profiles for Equation (12) with fixed temporal fractional order $\beta =1$ and varying spatial orders $\alpha =0.5$, $0.8$, and 1 is shown graphically Horizontal axis: space x (a.u.); vertical axis: $\left|u\right(x,t\left)\right|$. Decreasing $\alpha$ results in broader soliton profiles and lower peaks, reflecting enhanced spatial dispersion.

A visual illustration of a periodic Jacobi elliptic solution with $\sigma =-5.55,\gamma =0.85,\alpha =1,h=0.5,d_2=5,m=0.852$ for Equation (14) is presented in Figure 3. Jacobi elliptic soliton profiles based on Equation (14) for fixed $\alpha =1$ and varying $\beta =0.55$, $0.7$, and 1 is shown graphically. The axes show x (a.u.) versus $\left|u\right(x,t\left)\right|$. As $\beta$ increases, the waveform becomes more sharply defined with higher oscillation contrast, indicating weaker memory effects in time. The same parameter values are used in Figure 4, but with the difference that $\beta$=1 and various values of $\alpha$ are used to show the effect of the fractional derivative on space (x). Jacobi elliptic wave profiles from Equation (14) with fixed $\beta =1$ and spatial orders $\alpha =0.5$, $0.8$, and 1 is shown graphically. Axes represent space x (a.u.) vs. $\left|u\right(x,t\left)\right|$. Lower $\alpha$ values broaden the wave and reduce periodic sharpness, highlighting the influence of spatial nonlocality due to fractional dispersion. This algorithm generates solitary wave solutions that can travel great distances while maintaining their shape and velocity. The balance between the dispersion and nonlinear effects of the system leads to this exceptional stability.

Physical Relevance of Solutions

The analytical solutions derived in this study offer several physically meaningful insights into nonlinear optical systems with fractional dispersion and nonlocal effects. The key physical interpretations are summarized as follows:

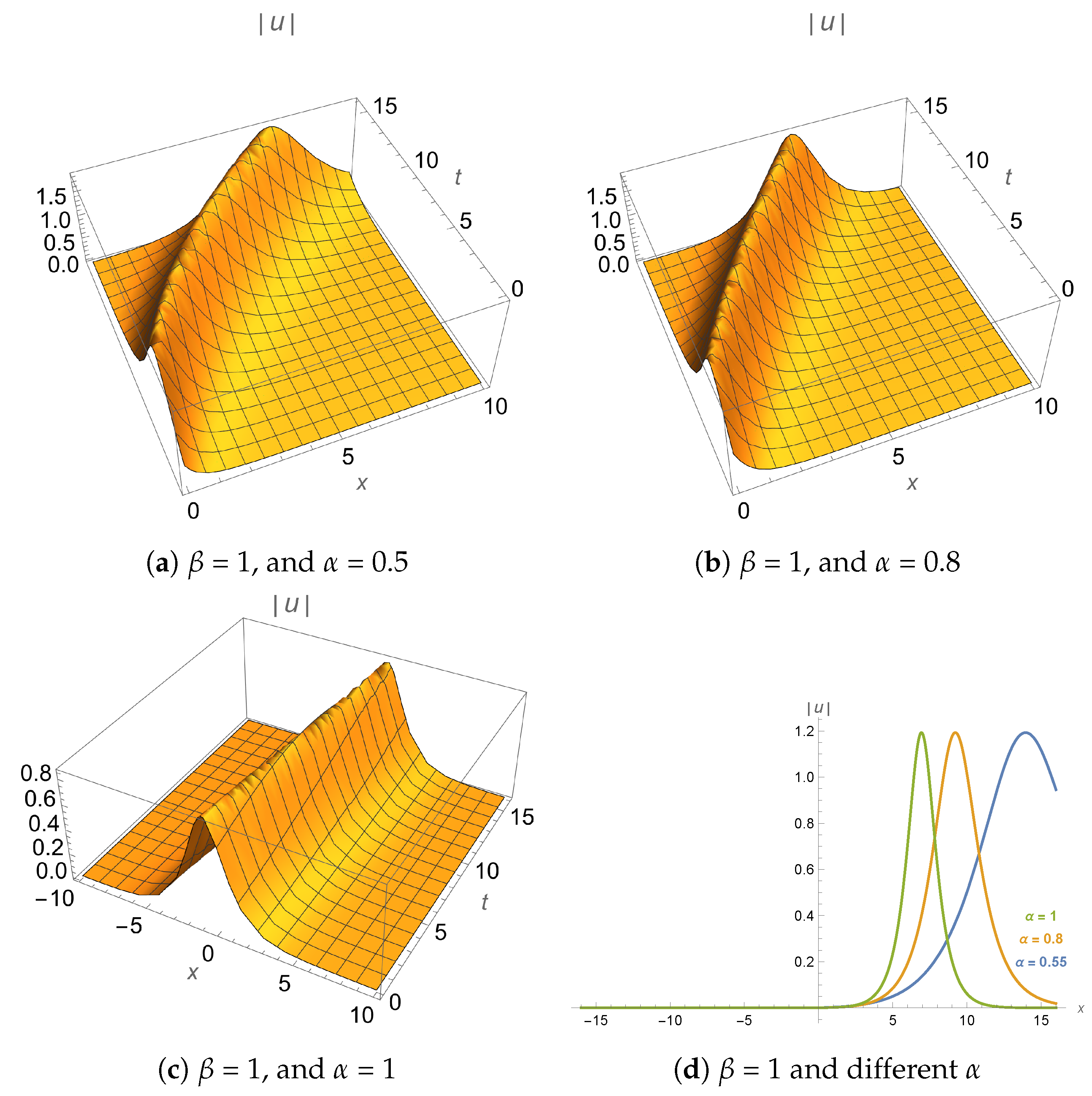
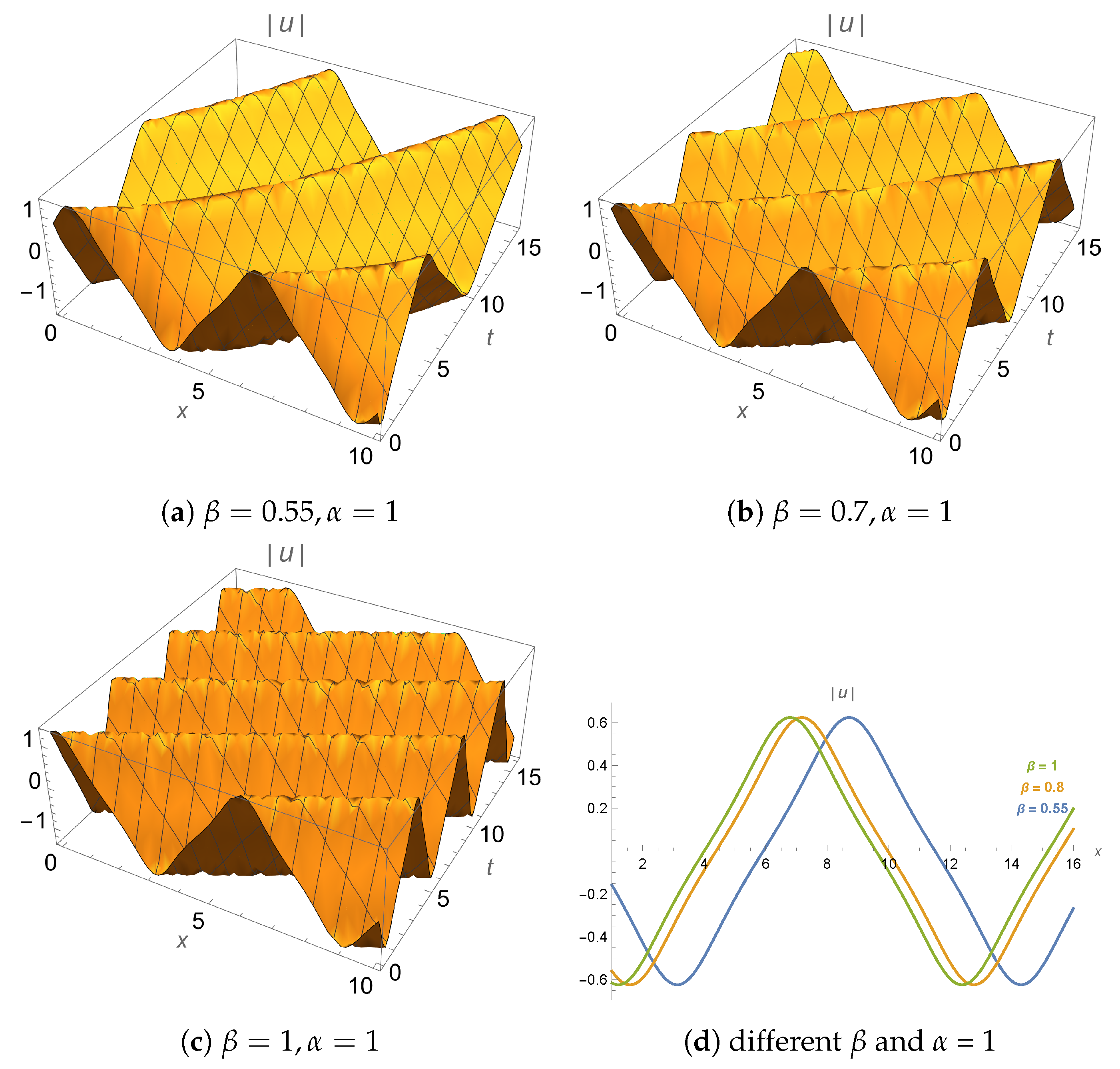
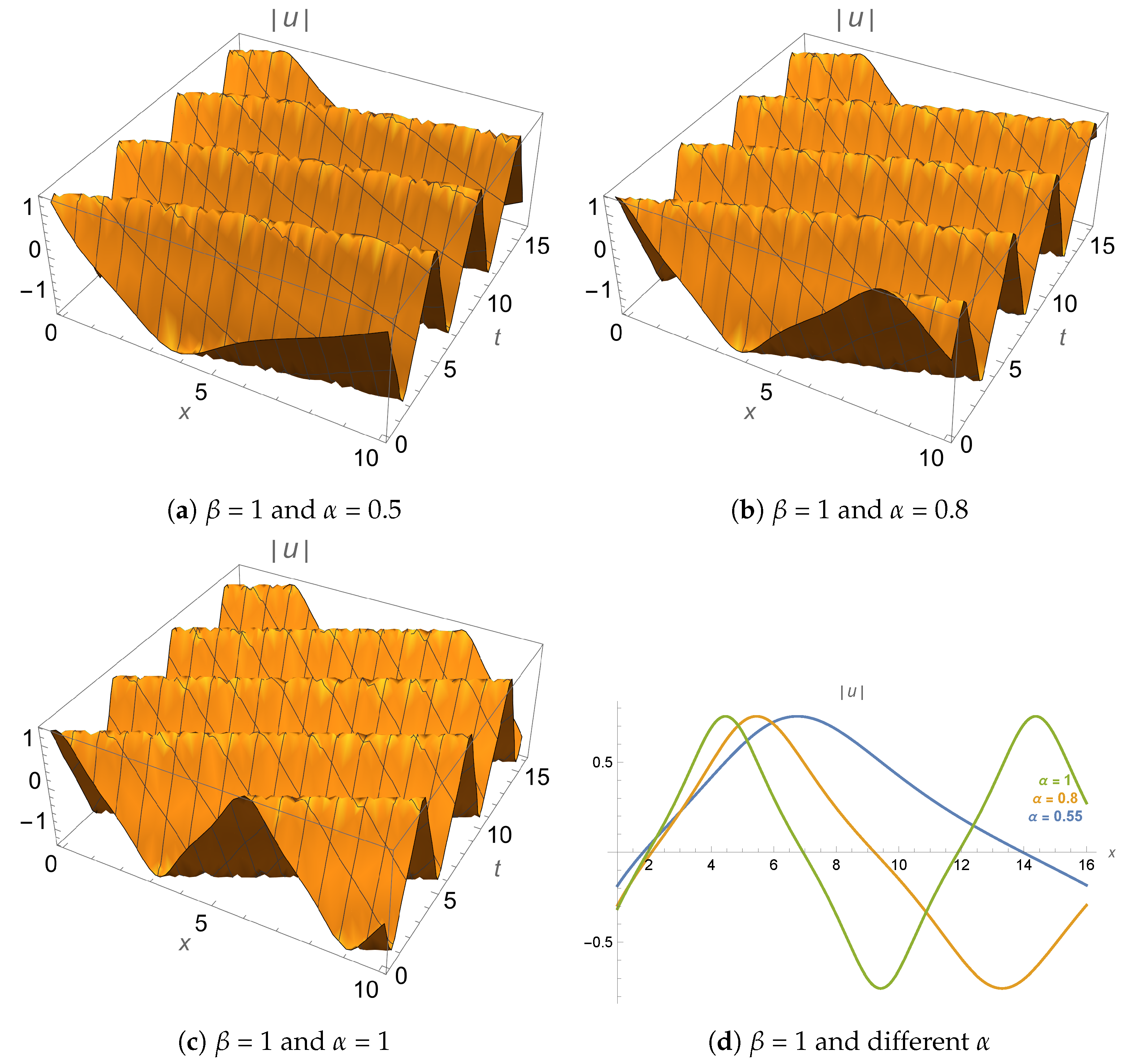
• Role of spatial fractional order $\alpha$: The parameter $\alpha$ governs the degree of anomalous spatial dispersion. As shown in Figure 2 and Figure 4, decreasing $\alpha$ results in broader wave profiles and reduced peak amplitudes, indicating enhanced spatial spreading. This behavior models long-range dispersive effects observed in fiber optics and photonic lattices.
• Role of temporal fractional order $\beta$: The parameter $\beta$ captures memory effects in the system. As demonstrated in Figure 1 and Figure 3, lower values of $\beta$ result in broader, more diffuse pulse shapes due to enhanced non-Markovian behavior. This is relevant for modeling ultrashort pulse propagation in media with temporal relaxation.
• Interpretation of bright soliton (Equation (12)): The bright soliton represents a localized pulse sustained by the balance between fractional dispersion and cubic–quintic nonlinearity. This is applicable in self-focusing media such as high-power laser systems and nonlinear fibers with tailored dispersion profiles.
• Interpretation of Jacobi elliptic solutions (Equation (14)): These solutions describe periodic waveforms, which may correspond to pulse trains or modulated structures in wavelength-division multiplexing (WDM) systems. The influence of $\alpha$ and $\beta$ on wave periodicity and sharpness is consistent with observed dispersion-induced distortions in experimental setups.
• Choice of parameters: The parameters $\sigma =2.95$, $\gamma =-1.6$, $h=0.66$, and $d_2=5.44$ were chosen to satisfy the solvability conditions of the IMETM. In physical terms, $\gamma <0$ captures self-focusing nonlinearities, and positive $\sigma$ reflects higher-order dispersion—a typical combination for modeling soliton propagation in cubic–quintic media. These values align with existing theoretical studies [30,31,32,33] and produce physically realistic waveforms.
• Real-world relevance: The flexibility of fractional orders allows for tailoring the solution behavior to match specific experimental scenarios, such as pulse compression, dispersion management, or long-distance propagation stability in nonlinear optical channels.

5. Conclusions

While classical hyperbolic methods have been applied to integrable models, their adaptation to higher-order systems with space–time fractional $\beta$-derivatives remains largely unexplored. This work fills that gap by employing the method to derive multiple classes of exact solutions for the fractional model with cubic–quintic interactions. The obtained solutions—including elliptic, exponential, and bright soliton forms—demonstrate the method’s effectiveness in addressing fractional nonlinear partial differential equations. The main novelty of this work lies in the derivation of new classes of exact analytical solutions to the higher-order fractional NLS equation using an extended tanh-function method tailored to handle space-time fractional derivatives. The incorporation of cubic–quintic and higher-order dispersion terms introduces rich dynamics, and the derived solutions provide insights into fractional wave propagation phenomena not addressed in earlier works. The inclusion of $\beta$-fractional derivatives enhances the modeling accuracy of wave propagation in media with anomalous dispersion, which is particularly relevant for telecommunications and nonlinear optics. Graphical simulations further confirm the stability and parameter sensitivity of these soliton solutions, offering practical insights for controlling dispersion and nonlinearity in optical systems. Beyond the model equation, the approach presented here holds potential for broader application to other nonlinear physical models involving fractional dynamics. The key takeaway of this work is that fractional-order derivatives, when combined with cubic–quintic nonlinearities and higher-order dispersion terms, significantly enrich the solution space of nonlinear wave models. The analytical framework provided here allows researchers to predict and design specific wave behaviors—such as pulse localization, periodicity, and memory-induced broadening—by tuning the fractional parameters $\alpha$ and $\beta$. Practically, this means that optical system designers can use these analytical insights to guide the configuration of dispersion-managed fibers, develop pulse-shaping strategies in nonlinear waveguides, or simulate fractional media with targeted soliton characteristics. The technique itself may be applied to other fractional PDEs beyond the nonlinear Schrödinger family, offering a versatile tool for theoretical exploration in nonlocal wave dynamics.

6. Future Work

Building on the analytical results presented in this study, several promising directions can be pursued in future research:

• Stability Analysis: A rigorous linear and nonlinear stability analysis of the derived soliton and periodic solutions, especially under perturbations in the fractional parameters $\alpha$ and $\beta$, would deepen understanding of solution robustness.
• Numerical Simulations: Implementing high-accuracy numerical schemes (e.g., spectral or finite difference methods) to simulate pulse dynamics and compare with the exact solutions derived here.
• Physical Modeling in Fibers: Calibrating the model parameters using experimental data from real-world optical fiber systems that exhibit anomalous dispersion and nonlocal effects.
• Multi-Component Systems: Generalizing the model to vector or coupled fractional NLS systems to study multi-mode wave propagation or polarization effects.
• Fractional Dissipation and Gain: Introducing fractional damping or gain terms to analyze the interplay between fractional dispersion and energy exchange in nonlinear media.

These directions would not only enrich the theoretical framework of fractional wave dynamics but also bridge the gap between analytical models and real-world photonic applications.