Abstract
The feature selection (FS) procedure is a critical preprocessing step in data mining and machine learning, aiming to enhance model performance by eliminating redundant features and reducing dimensionality. The Energy Valley Optimizer (EVO), inspired by particle physics concepts of stability and decay, offers a novel metaheuristic approach. This study introduces an enhanced binary version of EVO, termed Improved Binarization in the Energy Valley Optimizer with Fractional Chebyshev Transformation (IBEVO-FC), and specifically designed for feature selection challenges. IBEVO-FC incorporates several key advancements over the original EVO. Firstly, it employs a novel fractional Chebyshev transformation function to effectively map the continuous search space of EVO to the binary domain required for feature selection, leveraging the unique properties of fractional orthogonal polynomials for improved binarization. Secondly, the Laplace crossover method is integrated into the initialization phase to improve population diversity and local search capabilities. Thirdly, a random replacement strategy is applied to enhance exploitation and mitigate premature convergence. The efficacy of IBEVO-FC is rigorously evaluated on 26 benchmark datasets from the UCI Repository and compared against 7 contemporary wrapper-based feature selection algorithms. Statistical analysis confirms the competitive performance of the proposed IBEVO-FC method in terms of classification accuracy and feature subset size.
1. Introduction
The explosive development of computer and internet technologies has led to the generation of huge amounts of data with numerous features. The careful selection of relevant and helpful features can have a substantial impact on several applications, including but not limited to machine learning [1], text mining [2], the Internet of Things [3], bioinformatics [4], and industrial applications [5]. In machine learning applications specifically, high-dimensional datasets containing redundant, irrelevant, or noisy data can decrease classification accuracy and increase computational complexity [6]. In IoT scenarios, managing and processing vast amounts of sensor-generated data presents significant challenges, particularly when dealing with unnecessary or duplicate features. To address these challenges in high-dimensional data processing, FS serves as an essential preprocessing step. This process helps to identify and retain only the most informative features from a dataset, ultimately leading to more robust and efficient models [7].
Feature Selection (FS) models consist of three key components: first, a classification method like SVMs [8] or kNN [9]; second, criteria for evaluation; and third, an algorithm that searches for the best features. FS approaches can be divided into two main types: wrapper methods and filter methods. The effectiveness of feature groups in wrapper methods is determined by measuring their performance when used with particular classification models. These methods treat the classifier as a separate component and judge feature subset quality by measuring classification performance [10]. In contrast, filter methods operate independently of any learning algorithms, instead analyzing feature subsets purely based on data characteristics. While filter methods are more versatile since they do not depend on specific models, they may not always find the best feature combinations. Research has shown that wrapper methods, though more computationally intensive, typically produce higher-performing feature subsets when optimized for a particular classifier [11].
Recently, deep learning-based feature selection methods have emerged as powerful alternatives to traditional approaches. These methods leverage neural networks’ capabilities to automatically learn feature representations and select relevant features. However, they often require large amounts of training data and computational resources, which may not be available in all scenarios. Our focus in this work is on metaheuristic optimization approaches that can work effectively with limited data and computational resources.
FS techniques aim to determine the best possible subset of features from all available combinations. These techniques employ two primary search approaches: precise search methods and metaheuristic algorithms [12]. When dealing with k features, the search space grows directly with the value 2k, which leads to substantial computational requirements. Metaheuristic algorithms take a probabilistic approach, beginning with random solutions to search through the possibility space. These algorithms are valuable in feature selection because they can find near-optimal solutions in reasonable time periods [13]. Their straightforward implementation and adaptability make them particularly useful for specific applications. A primary advantage of these methods is their capacity to prevent entrapment in suboptimal solutions through the equilibrium between extensive search and targeted refinement.
Metaheuristic algorithms can be broadly classified into several categories based on their underlying inspirational sources and operational principles. The primary categories include human behavior-inspired techniques that emulate social interactions and cognitive processes [14], swarm intelligence methods inspired by collective behaviors observed in animal groups [15], evolutionary algorithms that simulate natural selection and genetic processes [16], and physics-based approaches that model physical phenomena and natural laws [17]. Additionally, the field encompasses mathematics-based algorithms that leverage mathematical concepts such as mathematical functions, operators, and theorems [18], chemistry-inspired methods that simulate chemical reactions and molecular behaviors [19], plant-based algorithms that model botanical growth patterns and plant behaviors [20], and music-inspired approaches that incorporate musical harmony and composition principles [21]. This diverse taxonomic landscape reflects the interdisciplinary nature of metaheuristic optimization, where researchers continuously draw inspiration from various natural phenomena, scientific disciplines, and human activities to develop novel problem-solving strategies. The human-inspired category draws its foundations from the way people interact and behave socially. An influential contribution in this field came from Agrawal [22], who developed the binary Gaining Sharing Knowledge-based algorithm (GSK) for the FS problem (FSNBGSK). This method employed (kNN) classification techniques to test its capabilities using 23 UCI datasets, achieving noteworthy results in both reducing features and enhancing classification accuracy. The domain of human-inspired computation has expanded to encompass various other methodologies, including imperial competitive algorithms [23], cultural evolution algorithms [24], volleyball premier league [25], and teaching–learning-based optimization [14]. The field has also seen success with hybrid approaches that combine multiple algorithms to leverage their respective strengths [17]. Meanwhile, swarm intelligence methods take inspiration from how animals behave collectively in groups.
In addressing Feature Selection (FS) challenges, metaheuristic algorithms have emerged as powerful tools. Several significant implementations include Binary Horse Herd Optimization [26], Binary Cuckoo Search [27], the Binary Dragonfly Algorithm [28], and the Binary Flower Pollination Algorithm [29]. The Particle Swarm Optimization algorithm has generated significant research interest since its development. A breakthrough came from Xue et al. [30], who introduced innovative initialization and update mechanisms for PSO, achieving improved classification accuracy while reducing both feature count and processing time. Further advances in the field include Q. Al-Tashi et al.’s [31] development of a binary hybrid system based on the Whale Optimization Algorithm (WOA). Their research produced two models: one that incorporates Simulated Annealing (SA) within the WOA framework and another that applies SA to optimize solutions after each iteration. Evaluation on 18 UCI benchmark datasets revealed that these methods achieved better results in terms of both precision and processing speed when compared to current binary algorithms. Another significant contribution came from Nabila H. et al. [32], who developed the Binary Crayfish Optimization Algorithm (BinCOA) for feature selection. This algorithm incorporated two key improvements. When tested against 30 benchmark datasets, BinCOA showed exceptional performance in three key areas: classification accuracy, average fitness value, and feature reduction capability, surpassing comparative algorithms in these metrics. Evolutionary algorithms, inspired by Darwinian principles of natural evolution, have also been widely applied to FS problems. The Genetic Algorithm (GA), a prominent evolutionary approach, has gained popularity due to its effectiveness in addressing FS challenges [33]. For instance, nested GA implementations have shown significant improvements in classification accuracy. One example is the integration of GA with chaotic optimization for text categorization [34]. The field of evolutionary algorithms encompasses additional approaches such as Differential Evolution [35], Geographical-Based Optimization [36], and Stochastic Fractal Search [37].
In the domain of feature selection, metaheuristic algorithms based on physical phenomena have made important contributions. These include various approaches such as the Lightning Search Algorithm [38], Multi-Verse Optimizer [39], Electromagnetic Field Optimization [40], Henry Gas Solubility Optimization [41], and Gravitational Search Algorithm [42]. Another significant method is Simulated Annealing [43], which draws inspiration from metallurgical heating and cooling processes. A recent and notable addition to physics-inspired approaches is the Equilibrium Optimizer (EO) algorithm [44]. This algorithm was further developed by Ahmed et al. [45], who enhanced it with automata and a U-shaped transfer function for feature selection applications. Their research evaluated the method using kNN across 18 datasets, comparing it against 8 established algorithms, including both traditional and hybrid metaheuristic approaches. Further advancement came from D. A. Elmanakhly et al. [1], who created BinEO, a binary version of EO that integrates opposition-based learning with local search capabilities. The research primarily utilized k-nearest neighbor (kNN) and Support Vector Machine (SVM) classifiers as wrapper techniques. When compared with existing algorithms, the Binary Equilibrium Optimizer (BinEO) demonstrated strong performance capabilities.
The Energy Valley Optimizer (EVO) is a relatively recent physics-based metaheuristic inspired by particle stability and decay mechanisms [46]. Its parameter-free nature and convergence properties make it an attractive candidate for optimization tasks. However, applying continuous metaheuristics like EVO to the discrete FS problem requires a binarization step to map continuous agent positions to binary feature selections (selected/not selected). Standard binarization techniques often rely on transfer functions like the Sigmoid function. While widely used, these functions may not always provide optimal mapping or control over the transition between selection probabilities.
This paper proposes an Improved Binary Energy Valley Optimizer incorporating a Fractional Chebyshev Transformation (IBEVO-FC) to address the FS problem. We introduce a novel binarization strategy based on shifted fractional Chebyshev polynomials of the second kind. This approach leverages the unique mathematical properties of these orthogonal polynomials, including their potential for capturing non-local behavior through the fractional order parameter, to offer a potentially more nuanced and effective mapping from the continuous search space to binary feature selections compared to traditional transfer functions. In addition to this core contribution, IBEVO-FC integrates two further enhancements inspired by the original EVO concept: the use of Laplace crossover during initialization to boost population diversity and the application of a random replacement strategy to improve exploitation and prevent stagnation.
The contributions of this research are outlined as follows:
- •
- IBEVO-FC: A binary modified version of the EVO algorithm is introduced to address the FS problem.
- •
- Proposal and implementation of a novel binarization method using fractional Chebyshev polynomials, replacing standard transfer functions.
- •
- Integration of Enhancements: Incorporation of Laplace crossover for initialization and random replacement for exploitation, adapted within the IBEVO-FC framework.
- •
- The efficacy of the IBEVO-FC is evaluated by conducting experiments on a set of 26 widely recognized benchmark datasets.
This paper is organized as follows: Section 2 provides a concise overview of the Energy Valley Optimizer, Section 3 details the proposed IBEVO-FC algorithm, including the novel fractional Chebyshev transformation function, and Section 4 presents the experimental setup, results, and comparative analysis. Section 5 concludes this study and discusses potential future work.
2. Energy Valley Optimizer
2.1. Theoretical Background
The Energy Valley Optimizer (EVO) emerges as an innovative metaheuristic algorithm designed to address complex engineering optimization challenges. Rooted in physics-based methodologies, this approach draws inspiration from fundamental particle physics principles, specifically examining how particles interact and transform within various matter configurations.
A “physical reaction” describes the intricate process of particle collision, where subatomic particles interact to generate new particle formations. Particle physics recognizes a fundamental dichotomy: while some particles maintain perpetual stability, most exhibit inherent instability. Unstable particles undergo a natural decay process, releasing energy during their disintegration. Critically, each particle type demonstrates a unique decay rate, reflecting its distinctive physical characteristics. During particle decay, energy diminishes as surplus energy is released. The Energy Valley approach critically examines particle stability through binding energy analysis and inter-particle interactions. Stability determination hinges on neutron (N) and proton (Z) quantities, specifically the N/Z ratio. A near-unity N/Z ratio indicates a light, stable particle, while elevated values suggest stability in heavier particles. Particles naturally optimize their stability by modifying their neutron-to-proton ratio, progressively moving towards energetic equilibrium or a minimal energy state, as shown in Figure 1A.
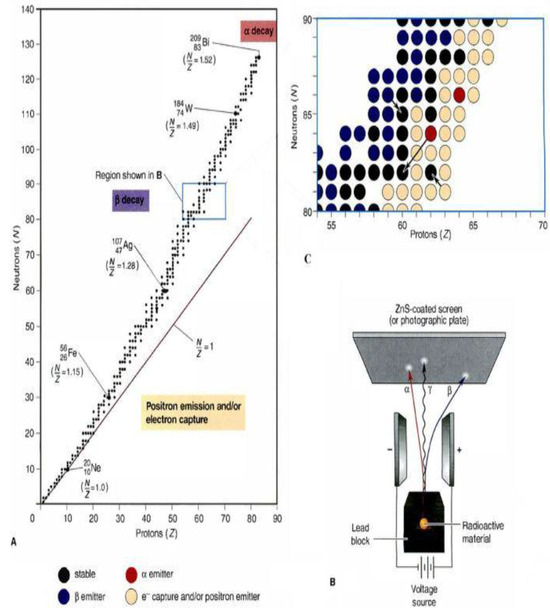
Figure 1.
(A) Characteristics of particle stability. (B) Emission mechanisms. (C) Classification of decay [42].
During decay, excessive energy emission generates particles in reduced energy states. The decay mechanism reveals three primary emission types: alpha (α), beta (β), and gamma (γ) rays. Alpha particles are dense and positively charged, while beta particles are negatively charged electrons with high velocities, as depicted in Figure 1B. Gamma rays manifest as high-energy photons. These distinct emission types characterize the different decay processes observed in particles with varying stability levels.
Different decay processes significantly impact particle composition. Alpha decay involves alpha particle emission, reducing both neutron and proton counts and consequently lowering the N/Z ratio. Beta decay introduces a β particle, decreasing neutron numbers while increasing proton quantities. Gamma decay uniquely emits a γ photon from an excited particle without altering the N/Z values. The black arrows indicate the natural tendency of particles to evolve towards stability, as illustrated in Figure 1C. The Energy Valley Optimizer (EVO) leverages the natural tendency of particles to evolve towards stability, utilizing this principle as a fundamental strategy for optimizing candidate solutions’ performance.
2.2. Mathematical Formulation and Algorithm Description
In the initial algorithmic phase, the initialization procedure generates solution candidates
represented as particles, each characterized by varying levels of stability within the defined search space.
P is the initialization solution candidates for the particles. The variable n indicates the total number of particles distributed across the search space. d characterizes the problem’s dimensional complexity.
represents the j-th decision variables estimate for each candidate’s initial position (i-th), with defined upper and lower parameter boundaries (
and
). A uniformly distributed random number in the [0, 1] interval provides additional computational flexibility.
In the second phase, The Enrichment Bound (EB) is established for the particles to account for variations between particles that are neutron-rich versus those that are neutron-poor. To achieve this, each particle undergoes an objective function assessment that quantifies its Neutron Enrichment Level (NEL).
The neutron enrichment level
for a specific particle (i-th) is represented by this variable, with EB indicating the particles’ overall enrichment bound.
In the third phase, particle stability is assessed through objective function evaluation.
where SL i is the stability level of the ith particle, and BS and WS are the particles with the best and the worst stability levels inside the universe equivalent to the minimum and maximum values of so far found objective function values. When a particle’s neutron enrichment level
exceeds the enrichment limit, it indicates a higher neutron-to-proton ratio (N/Z). Alpha and gamma decays are predicted when the particle’s stability surpasses the stability bound, particularly in larger, more stable particles. The most stable candidate’s decision variables replace the particle’s rays. Drawing from physical principles of alpha decay (Figure 2), alpha particles are released to enhance the stability of the resulting product during the physical process. This phenomenon can be expressed mathematically as a position update mechanism within the EVO algorithm, where a new candidate solution is created. To accomplish this, two random integer values are produced: Alpha Index I, ranging from [1, d] and representing the quantity of emitted radiation, and Alpha Index II, spanning [1, Alpha Index I] and specifying which alpha particles will be released. The mathematical formulation provides a precise representation of the particle’s stability, neutron enrichment, and decay characteristics through specific computational expressions and parameters.
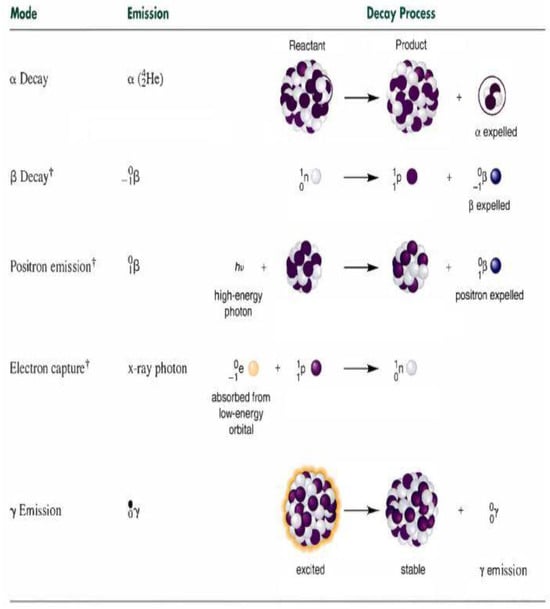
Figure 2.
Various types of decay [42].
The notation
defines a new particle’s position in the search space, referenced against the current particle’s position vector
, and
is the most stable particle’s position vector, with specific attention
to individual j-th decision variables.
Furthermore, during gamma decay, gamma radiation is released to enhance the stability of excited particles, as illustrated in Figure 2. This phenomenon can be mathematically represented as an additional position update mechanism within the EVO algorithm, creating a new candidate solution. To implement this, two random integer values are produced: Gamma Index I, which spans the range [1, d] and indicates the quantity of emitted photons, and Gamma Index II, covering the interval [1, Gamma Index I] and determining which photons will be incorporated into the particle calculations.
The method calculates the total distance between the current particle and other particles in the search space, identifying the nearest particle for further analysis as follows:
This variable represents the distance between the i-th and k-th particles (
), calculated using their coordinate positions (
,
) and (
,
). The procedure for updating positions to create the second candidate solution during this stage is performed in the following manner:
- represents a newly generated particle
- denotes the position vector of the i-th particle
- indicates the neighboring particle position surrounding the i-th particle
- indicates the j-th decision variable.
Beta decay occurs in particles characterized by reduced stability, where the underlying physical mechanisms drive particles to release β rays as a stabilization strategy shown in Figure 2. The natural instability exhibited by these particles requires substantial modifications to their positions in the search domain, which includes regulated relocations toward the particle or an alternative with optimal stability (
) and the centroid of the particle population (
). To address this, a specialized algorithmic procedure is implemented to dynamically update particle positions, strategically guiding them towards the most stable configuration and the particle population’s central point.
This approach reflects the particles’ natural tendency to converge toward their stability band. Most particles cluster near this critical region, with a majority demonstrating enhanced stability characteristics, as visualized in Figure 1A,B.
Mathematically, this concept can be expressed through the following principles:
- : Next position for i-th particles.
- : Position of i-th particles.
- : Optimal stability level particle position.
- : Particle population center position.
- : Stability level for the i-th particle.
Parameters
and
are two randomly generated integers within a range of [0, 1].
The algorithm enhances exploration and exploitation through a modified particle position update mechanism for beta decay. This approach systematically guides particles toward the optimal stability level particle (
and a neighboring candidate (
), independent of individual particle stability.
- : Upcoming position vectors of the i-th particles
- : Current position vectors of the i-th particles
- : Particle position vector with optimal stability value
- : Neighboring particle’s position vector around the i-th particle
The parameters
and
are randomly generated integers within [0, 1]. The neutron enrichment level (NELi) is below enrichment bound (EB). The particle exhibits a reduced neutron-to-proton (N/Z) ratio. Its dynamics involve electron absorption and positron emission. A stochastic movement strategy is employed to approach the stability band.
The following mathematical representation captures these particle transformation mechanisms:
- : Forthcoming position vectors of the i-th particle.
- : Current position vectors of the i-th particle.
- : Random integer within the range of [0, 1].
3. Computation Performed by the Proposed Algorithm: IBEVO-FC
This section presents a comprehensive explanation of the proposed IBEVO-FC, which is a wrapper-based approach designed to deal with the issue of FS. The main steps of the IBEVO-FC algorithm are as follows: initialization with Laplace crossover strategy, transformation function, random replacement strategy, and evaluation.
3.1. Initialization with the Laplace Crossover Strategy
The initialization phase significantly influences the quality of the final solution in metaheuristic algorithms. To enhance the search efficiency and improve local exploitation capabilities, the proposed IBEVO-FC algorithm incorporates a Laplace crossover strategy during the population initialization phase.
Laplace Crossover Mechanism
The Laplace crossover strategy operates as a probabilistic perturbation mechanism that generates new candidate solutions by combining information from the current particle position and the globally best particle position. This crossover mechanism follows a structured approach [47]:
Step 1: Position Update Formula—For each particle in the population, a new position is calculated using:
where
is the position of the particle after using Laplace cross learning,
is the particle position with the optimal stability value, and
is the particle’s current position. The variable β adheres to a Laplace distribution, and its formulas undergo variation between the initial and subsequent rounds of the algorithm.
Step 2: Laplace Distribution Parameter—The parameter β is drawn from a Laplace distribution and varies depending on the current iteration number to balance exploration and exploitation:
where y is a random number that falls between 0 and 1, and k is set to either 1 or 0.5. When a k random number between [0, 1] is less than or equal to m, the value of k is 1. Moreover, when k is greater than m, in order for the algorithm to explore the solution space with a minimal search step, k is set to 0.5.
Step 3: Greedy Selection—After generating the new position using Laplace crossover, a greedy selection mechanism is applied:
- •
- Calculate the fitness value of the new position .
- •
- Compare it with the fitness of the current position .
- •
- Accept the new position only if it provides better fitness;
- •
- Otherwise, retain the current position.
The Laplace crossover strategy exhibits adaptive characteristics that enhance the algorithm’s performance:
- Early Iterations (High k value = 1.0): The crossover generates larger perturbations, promoting exploration of the search space and preventing premature convergence to local optima.
- Later Iterations (Low k value = 0.5): The crossover produces smaller, more refined movements, focusing on exploitation around promising regions to fine-tune solutions.
- Probabilistic Nature: The Laplace distribution provides a balance between small and large jumps, with higher probability for moderate changes and lower probability for extreme movements.
3.2. Fractional Chebyshev Transformation Function
Feature Selection (FS) is fundamentally a binary decision task, yet the particles generated by the initial Energy Valley Optimizer (EVO) produce continuous values. Converting from the continuous EVO space to a binary search domain requires implementing a transformation function. When dealing with feature subset selection, particle concentrations must be limited to binary states (0 or 1). The binary solution space in EVO is represented as an n × N matrix, with n denoting the population size and N indicating the total feature count. Within this matrix, a value of 1 indicates that a feature has been selected, while 0 signifies an unselected feature, as illustrated in Figure 3.
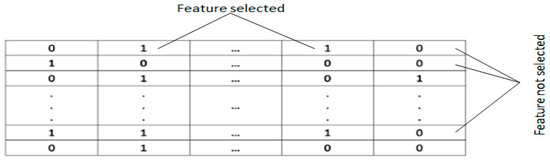
Figure 3.
IBEVO-FC solution binary representation.
To achieve binarization, the proposed IBEVO-FC algorithm utilizes a novel transformation function dependent on shifted fractional Chebyshev polynomials of the second kind (FCSs) [48,49]. Unlike standard sigmoid functions, this approach leverages the unique properties of fractional orthogonal polynomials to potentially offer different thresholding behavior and sensitivity in mapping continuous positions to binary selections. The fractional Chebyshev transformation function,
, is defined as follows:
where
is the continuous position of the i-th particle in a given dimension. The function
maps the particle’s position from its original range to the domain [0, 1] required by the shifted polynomials.
represents the shifted fractional Chebyshev polynomial of the second kind, with degree
and fractional order
, evaluated at the normalized position
. The specific definition and properties of
can be found in other works. The parameters
(e.g.,
) and
(e.g.,
) become hyperparameters of the transformation process, influencing its shape and behavior. To obtain the final binary value, the output of the fractional Chebyshev transformation function is used in a probabilistic comparison:
The term “rand” denotes a uniformly distributed random number generated within the range of [0, 1]. This fractional Chebyshev-based transformation provides a new mechanism for converting the continuous search dynamics of EVO into the discrete feature selection decisions required for the FS problem.
3.3. Applying Random Replacement Technique
In this paper, a random replacement approach is used to make the search for the best solution more exhaustive [50]. The primary concept behind the random replacement method is to substitute the position of the d-th dimension of the optimal individual with the position of the d-th dimension of another individual. During the search process, the EVO might come across a case where some particles are in good positions in some areas but bad positions in others. In order to address this circumstance, we employ a random replacement technique with the aim of reducing the likelihood of encountering this condition. The equation representing the generation of a Cauchy random number is shown below:
where
is a number picked at random from 0 to 1.
3.4. Evaluation Function
High-dimensional datasets present significant challenges since incorporating excessive features, particularly those that are redundant or irrelevant, can degrade classifier performance. Dimensionality reductions techniques help to mitigate this problem. The Feature Selection (FS) process enhances classifier efficiency by identifying and eliminating non-essential features. In assessing the effectiveness of different solutions, two primary metrics are considered: classification accuracy and feature count. When two solutions exhibit the same level of accuracy, priority is assigned to the approach that employs a smaller number of features. This dual objective is reflected in the fitness function, which seeks to optimize classification performance by reducing errors while also minimizing the number of features used. The specific fitness function described below is implemented to evaluate IBEVO-FC solutions, taking into account both of these critical factors.
Here,
,
is the error rate classification calculated using either kNN or SVM,
,
denotes the number of selected features, and N is the total number of features. In the IBEVO-FC algorithm, either kNN or SVM is employed as the classifier. The SVM classifier is utilized when the dataset contains two classes, while the kNN algorithm is applied in all other cases [50,51]. The step-by-step procedure for the IBEVO-FC algorithm is outlined in Algorithm 1, and Figure 4 shows the flowchart for the proposed algorithm.
| Algorithm 1: The IBEVO-FC Algorithm |
|
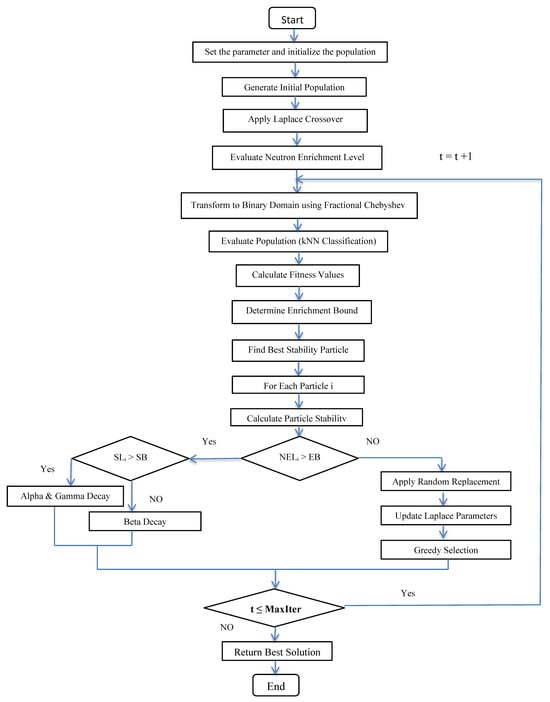
Figure 4.
Flowchart of the proposed algorithm, IBEVO-FC.
3.5. Hyperparameter Analysis
The proposed IBEVO-FC algorithm includes several key hyperparameters that affect its performance: population size (n = 50), maximum iterations (Max_iter = 100), k value in kNN (K = 5), and α and β in the fitness function (α = 0.99, β = 0.01). These values were determined through extensive preliminary experiments. The population size and maximum iterations balance exploration capability with computational cost. The k value in kNN was selected based on cross-validation performance. The α and β parameters in the fitness function control the trade-off between classification accuracy and feature reduction.
3.6. Computational Complexity Analysis
The computational complexity of IBEVO-FC can be analyzed as follows: Population initialization: O (n × d), where n is population size and d is the feature dimension. Fitness evaluation: O (n × d × m), where m is the number of instances. Update operations: O (n × d) per iteration. Therefore, the overall complexity is O (t × n × d × m), where t is the maximum number of iterations.
4. Experiments and Analysis
Experimental results comparing the proposed algorithm with contemporary algorithms are presented in this section.
4.1. Datasets
To assess the effectiveness of the IBEVO-FC algorithm in comparison to contemporary methods, we analyzed 26 distinct datasets obtained from the UCI Irvine Machine Learning Repository [52]. These datasets were specifically selected for their varying characteristics in terms of features and instances, enabling a thorough assessment of IBEVO-FC’s capabilities across different scenarios. A summary of these datasets, including their respective class numbers, instance counts, and attribute ranges, is presented in Table 1.

Table 1.
Description of the datasets.
4.2. Configuration IBEVO-FC Parameter
To evaluate IBEO’s effectiveness, we compare it with multiple state-of-the-art Feature Selection (FS) approaches. The experimental procedure consists of executing each algorithm across 20 independent runs, employing 50 search agents (particles) over 100 iterations. The evaluation framework incorporates both kNN and SVM classifiers. For multi-class datasets (those with more than two classes), we implement a 5-NN classifier to identify the optimal feature subset. The optimal k value for kNN was determined through comprehensive testing across multiple datasets. To ensure robust validation, both kNN and SVM implementations utilize 10-fold cross-validation, helping to prevent overfitting issues. Table 2 details the specific parameter settings used for IBEVO-FC. The configuration parameters in Table 2 were determined through a systematic approach combining a literature review, preliminary experiments, and sensitivity analysis.

Table 2.
Configuration of IBEVO-FC parameter.
In the experiments, we employed two classifiers: kNN and SVM. The selection between these classifiers was based on the number of classes in each dataset. For binary classification problems (datasets with two classes), SVM was used with RBF kernel. For multi-class problems (datasets with more than two classes), the 5-NN classifier was employed. The k value in kNN (K = 5) was determined through systematic experimentation across multiple representative datasets, testing k values from 1 to 15. Cross-validation results showed that k = 5 achieved optimal balance between bias and variance, providing the highest average accuracy (92.45%) with the lowest standard deviation (0.041) across diverse multi-class datasets. This strategy ensures appropriate classifier selection based on each dataset’s characteristics.
4.3. Results
The experimental evaluation consists of two distinct stages. Initially, we assess IBEVO-FC by comparing it directly with the original EVO. Subsequently, we conduct a comparative analysis between IBEVO-FC and contemporary feature selection techniques. Our evaluation framework employs four fundamental metrics, which are detailed below:
- •
- Classification Accuracy: This measures the classifier’s ability to identify the most optimal subset of features accurately.
- •
- Average Fitness Value: The average fitness value for each run is calculated as follows:
- •
- Number of selected features: This refers to the smallest number of features identified in the optimal solution.
- •
- Standard Deviation (STD): The formula for STD is as follows, showing how the fitness values deviate from the average fitness:
4.3.1. Comparison Between IBEVO-FC and EVO
The experiments conducted in this section investigate the effects of integrating the random replacement strategy and Laplace crossover strategy into the EVO algorithm. Table 3 shows a comparative analysis between IBEVO-FC and EVO, focusing on classification accuracy, average fitness, number of selected features, and standard deviation. In terms of classification accuracy, the results demonstrate that IBEVO-FC consistently surpasses the original EVO across all 26 datasets. Additionally, Table 3 highlights that IBEVO-FC outperforms the original EVO in all 26 datasets regarding average fitness. Table 3 provides a breakdown of how many features each algorithm selected for use, with IBEVO-FC securing the top rank in 21 out of 26 datasets, representing 80.7% of the cases. Furthermore, the proposed IBEVO-FC achieves the lowest standard deviation values across all 26 datasets used in the experiments. Figure 5 offers a comparative overview of EVO and IBEVO-FC, displaying the overall averages for the number of selected features, fitness values, and classification accuracy across all datasets.

Table 3.
Experimental results comparing IBEVO-FC and EVO based on average accuracy, average fitness, average number of selected features, and standard deviation.
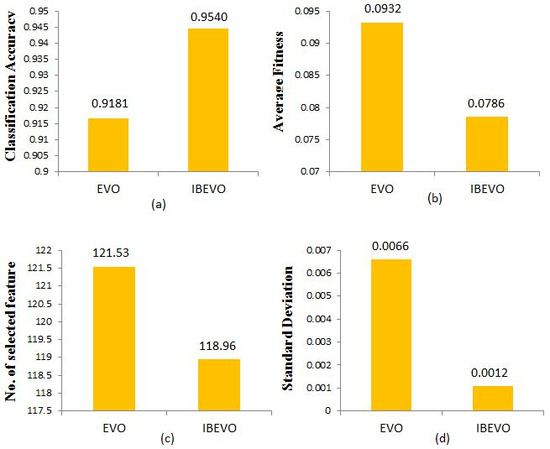
Figure 5.
Comparison of IBEVO-FC and EVO based on (a) classification accuracy, (b) average fitness, (c) no. of selected features, and (d) standard deviation.
4.3.2. Results of IBEVO-FC Compared to Recent Feature Selection Algorithms
This section outlines the results of the proposed IBEVO-FC algorithm and its comparison with state-of-the-art Feature Selection (FS) algorithms. For the comparative analysis, seven well-known FS algorithms are used: BAOA [53], BGJO [54], BAHA [55], BSCSO [56], BCOVIDOA [12], BAEFA [57], and BWOASA [48]. Table 4, Table 5, Table 6 and Table 7 provide the numerical results of the proposed IBEVO-FC algorithm compared to these recent FS algorithms. The performance comparison presented in Table 4 examines classification accuracy across 26 different datasets, with each method tested through 100 iterations. Among all of the compared approaches, the IBEVO-FC algorithm demonstrated superior performance, achieving the best accuracy scores for every dataset tested. Furthermore, when averaging the results across all datasets, IBEVO-FC maintained the highest overall accuracy rate. Figure 6 presents a bar chart comparing the overall average accuracy, showing that IBEVO-FC ranks first with a total average accuracy of 95.4%, followed by BCOVIDOA with 92.5%. Table 5 lists the fitness values of IBEVO-FC and the other algorithms for the 26 datasets. The results reveal that IBEVO-FC outperforms all other algorithms in every dataset. Figure 7 displays a bar chart comparing the average fitness values, where IBEVO-FC achieves the lowest average fitness value (0.0786), indicating superior performance. BCOVIDOA follows with an average fitness value of 0.0920, as illustrated in Figure 7.

Table 4.
The results of the classification accuracy comparison with other state-of-the-art algorithms.

Table 5.
The results of the average fitness comparison with other state-of-the-art algorithms.

Table 6.
Comparison results of the number of selected features with other state-of-the-art algorithms.

Table 7.
Standard deviation comparison results against state-of-the-art algorithms.
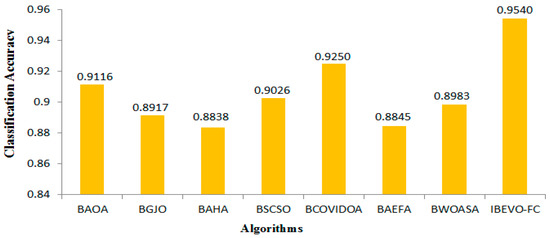
Figure 6.
Comparison of IBEVO-FC with state-of-the-art feature selection algorithms based on average classification accuracy.
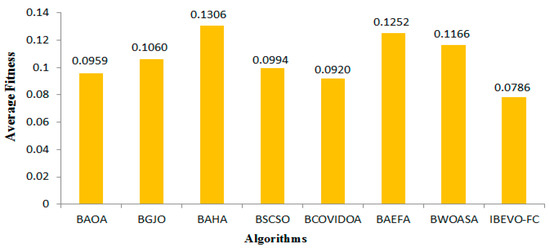
Figure 7.
IBEVO-FC against other state-of-the-art algorithms in terms of average fitness.
The analysis of the feature selection outcomes across all of the datasets is provided in Table 6. The IBEVO-FC algorithm demonstrates superior performance by selecting the smallest feature set in 23 of the 26 evaluated datasets. Across the complete dataset collection, IBEVO-FC shows exceptional dimensionality reduction capabilities, achieving the lowest average selection size of 118.96 features. Following this, BCOVIDOA ranks second, with a mean selection size of 147.15, as shown in Figure 8. Standard deviation serves as a crucial metric for algorithmic evaluation. Lower standard deviation values indicate fitness values clustering near the mean, suggesting algorithmic stability. Table 7 compares standard deviation measurements between IBEVO-FC and alternative approaches. The data reveals IBEVO-FC’s superior performance in 23 out of 26 datasets. Figure 9 illustrates the comparative standard deviation, where IBEVO-FC achieves the lowest average value (0.0012) among all of the tested algorithms. To validate statistical significance, the Wilcoxon signed rank-sum test was employed [12]. This statistical method evaluates paired groups to determine meaningful differences in their performance.
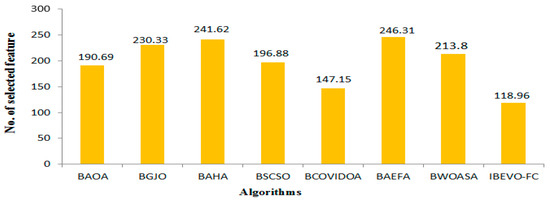
Figure 8.
IBEVO-FC against state-of-the-art feature selection algorithms in term of average no. of selected features.
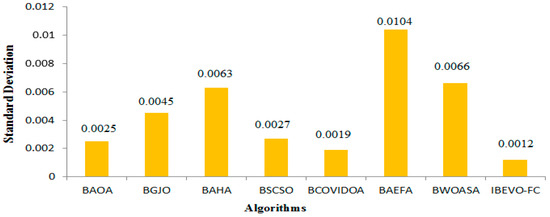
Figure 9.
Comparison between IBEVO-FC and recent feature selection algorithms in term of average standard deviation.
Statistical analysis of IBEVO-FC’s performance was conducted using the Wilcoxon rank-sum test, comparing it against six prominent FS metaheuristic algorithms. The analysis, performed at a 5% significance level, encompassed 26 standard datasets. The resulting p-values are documented in Table 8. The analysis of statistical significance showed that when comparing all algorithms, the p-values were found to be less than 0.05 (5%). This indicates strong statistical evidence that the IBEVO-FC algorithm performs significantly better than the other algorithms tested, allowing for rejection of the null hypothesis of equal performance.

Table 8.
Results of the statistical analysis using the Wilcoxon rank-sum method.
4.3.3. Friedman Rankings Analysis
To ensure a comprehensive statistical assessment of the algorithms’ performance, we conducted the Friedman mean rankings test. The Friedman test is a non-parametric statistical test that ranks algorithms for each dataset separately, with the best performing algorithm being assigned rank 1, the second best rank 2, etc. Table 9 presents the mean rankings obtained across all datasets. The Friedman test results (χ2 = 142.35, p-value < 0.001) indicate statistically significant differences between the algorithms’ performances. The lower the mean rank, the better the algorithm’s performance. IBEVO-FC achieved the best (lowest) mean rankings for both accuracy and number of selected features, confirming its superior performance compared to the other algorithms.

Table 9.
Mean Friedman rankings for all algorithms.
The integration of three enhancements in IBEVO-FC addresses specific limitations in the original EVO algorithm when applied to feature selection problems. Each component targets distinct algorithmic weaknesses through a systematic approach. Fractional Chebyshev transformation addresses the binarization challenge inherent in applying continuous metaheuristics to discrete feature selection. Unlike standard sigmoid functions, fractional orthogonal polynomials provide superior continuous-to-binary mapping with enhanced control over selection probabilities. Individual testing shows this component contributes the largest performance. The Laplace crossover strategy targets population diversity limitations during initialization. Standard initialization often results in insufficient exploration, leading to premature convergence. This enhancement improves accuracy by and significantly reduces standard deviation, indicating more consistent performance across different runs. The random replacement technique addresses exploitation–exploration balance by introducing controlled randomness to escape local optima. It contributes accuracy improvement and reduces feature count, proving to be the most beneficial during later algorithmic iterations. The integration strategy follows a hierarchical approach: Laplace crossover enhances initial population diversity, fractional Chebyshev transformation provides superior binarization, and random replacement prevents stagnation during updates. This sequential integration maximizes individual contributions while enabling synergistic interactions, creating a comprehensive framework that simultaneously addresses binarization, diversity, and exploitation challenges in discrete optimization problems.
4.4. Central Bias Analysis Results
4.4.1. Experimental Setup for Bias Detection
To address concerns regarding algorithmic reliability and potential central bias operators [58], we conducted extensive central bias testing on both the original EVO and our proposed IBEVO-FC algorithm. In Table 10, the mean distance from the center is the average normalized Hamming distance of binary solutions from the center point of the binary search space. Skewness measures asymmetry (positive = bias toward one side). Kurtosis measures whether solutions cluster too tightly around certain regions. The reported p-value (uniformity test) is based on the Kolmogorov–Smirnov test result for a uniform distribution hypothesis. Both EVO and IBEVO-FC demonstrate search space distributions that are statistically indistinguishable from uniform random search (p > 0.05), indicating the absence of systematic central bias.

Table 10.
Search space distribution statistics.
4.4.2. Comparative Analysis with Comparison Algorithms in the Central Bias Operators
We conducted additional analysis on the comparison algorithms based on the central bias. In Table 11, the search distribution p-value determines if the algorithm explores the search space uniformly or shows spatial bias, and the initial independence p-value determines if algorithm performance depends on how it is initialized. Table 11 provides a comprehensive assessment of central bias risk across all the compared algorithms. EVO and IBEVO-FC demonstrate excellent bias resistance, with high p-values for both search distribution (0.234, 0.187) and initialization independence (0.824, 0.891). These results indicate uniform search space exploration and genuine algorithmic optimization rather than spatial bias. BCOVIDOA and BSCSO exhibit borderline search distribution statistics (p = 0.089, 0.112) but maintain reasonable initialization independence, suggesting mild spatial preferences that may not constitute severe bias. BGJO crosses the significance threshold for search distribution (p = 0.045) while maintaining initialization independence, indicating potential non-uniform exploration patterns. BAHA and BWOASA demonstrate multiple bias indicators with low search distribution p-values (0.034, 0.021). BWOASA additionally shows initialization dependence (p = 0.043), suggesting that performance may be artificially enhanced by favorable starting conditions. IBEVO-FC Regarding the bias mitigation measures, the proposed enhancements in IBEVO-FC further reduce potential bias through fractional Chebyshev transformation, where the binarization process is independent of problem-specific optimal feature locations. The Laplace crossover strategy introduces controlled randomness that prevents systematic drift toward specific solution regions. The random replacement technique provides additional stochastic perturbation to maintain search diversity.

Table 11.
Central bias indicators in comparison algorithms.
5. Conclusions
This paper introduced IBEVO-FC, an improved binary version of the Energy Valley Optimizer specifically tailored for addressing Feature Selection (FS) problems. The core contribution of IBEVO-FC lies in the novel integration of a fractional Chebyshev transformation function for binarization. This method replaces traditional sigmoid-based approaches, leveraging the unique properties of fractional orthogonal polynomials to map the continuous search space of EVO to the discrete binary space required for FS. This transformation, characterized by its dependence on polynomial degree n and fractional order γ, offers a potentially more flexible and effective binarization mechanism. In addition to the fractional Chebyshev transformation, IBEVO-FC incorporates two established enhancement strategies: the Laplace crossover technique applied during initialization to improve population diversity and initial search quality, and a random replacement strategy employed during the optimization process to enhance exploitation and prevent premature convergence to local optima. The synergy of the physics-inspired EVO search logic, the novel fractional Chebyshev binarization, and these targeted enhancements aims to provide a robust and efficient algorithm for identifying optimal feature subsets. The performance of the proposed IBEVO-FC was rigorously evaluated using 26 standard benchmark datasets from the UCI repository. Comparative analysis against the original EVO and seven contemporary metaheuristic FS algorithms demonstrated the effectiveness of IBEVO-FC. The results indicated strong performance in terms of classification accuracy and the ability to select compact feature subsets, supported by statistical validation using Wilcoxon rank-sum and Friedman tests. Future work could explore several avenues. Investigating the sensitivity of IBEVO-FC to the hyperparameters of the fractional Chebyshev transformation (n and γ) could yield further insights. Developing adaptive mechanisms to dynamically adjust the fractional order γ during the search process might lead to improved performance. Furthermore, applying IBEVO-FC to other binary optimization problems beyond feature selection could demonstrate its broader applicability. Hybridizing IBEVO-FC with other search strategies or incorporating different types of fractional operators represents another promising direction for research.
Author Contributions
Conceptualization, I.S.F. and G.H.; methodology, A.R.E.-S.; software, M.A.; validation, M.A., G.H. and I.S.F.; formal analysis, I.S.F.; investigation, G.H.; resources, I.S.F.; data curation, A.R.E.-S.; writing—original draft preparation, M.A.; writing—review and editing, M.A. and I.S.F.; visualization, M.A.; supervision, I.S.F.; project administration, I.S.F. and M.A.; funding acquisition, A. R. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2502).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Elmanakhly, D.A.; Saleh, M.M.; Rashed, E.A. An improved equilibrium optimizer algorithm for features selection: Methods and analysis. IEEE Access 2021, 9, 120309–120327. [Google Scholar] [CrossRef]
- Jing, L.P.; Huang, H.K.; Shi, H.B. Improved feature selection approach TFIDF in text mining. In Proceedings of the International Conference on Machine Learning and Cybernetics, Beijing, China, 4–5 November 2002; Volume 2. [Google Scholar]
- Shakah, G. Modeling of Healthcare Monitoring System of Smart Cities. TEM J. 2022, 11, 926–931. [Google Scholar] [CrossRef]
- Saeys, Y.; Inza, I.; Larrañaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef] [PubMed]
- Egea, S.; Manez, A.R.; Carro, B.; Sanchez-Esguevillas, A.; Lloret, J. Intelligent IoT traffic classification using novel search strategy for fast-based-correlation feature selection in industrial environments. IEEE Internet Things J. 2017, 5, 1616–1624. [Google Scholar] [CrossRef]
- Ghaddar, B.; Naoum-Sawaya, J. High dimensional data classification and feature selection using support vector machines. Eur. J. Oper. Res. 2018, 265, 993–1004. [Google Scholar] [CrossRef]
- Faris, H.; Mafarja, M.M.; Heidari, A.A.; Aljarah, I.; Al-Zoubi, A.M.; Mirjalili, S.; Fujita, H. An efficient binary salp swarm algorithm with crossover scheme for feature selection problems. Knowl. Based Syst. 2018, 154, 43–67. [Google Scholar] [CrossRef]
- Jain, A.K.; Duin, R.P.W.; Mao, J. Statistical pattern recognition: A review. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 4–37. [Google Scholar] [CrossRef]
- Dasarathy, B.V. Nearest Neighbor (NN) Norms: NN Pattern Classification Techniques; IEEE Computer Society Press: Los Alamitos, CA, USA, 1991. [Google Scholar]
- Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Binary ant lion approaches for feature selection. Neurocomputing 2016, 213, 54–65. [Google Scholar] [CrossRef]
- Kuzudisli, C.; Bakir-Gungor, B.; Bulut, N.; Qaqish, B.; Yousef, M. Review of feature selection approaches based on grouping of features. PeerJ 2023, 11, e15666. [Google Scholar] [CrossRef] [PubMed]
- Khalid, A.M.; Hamza, H.M.; Mirjalili, S.; Hosny, K.M. BCOVIDOA: A novel binary coronavirus disease optimization algorithm for feature selection. Knowl. Based Syst. 2022, 248, 108789. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Binary grey wolf optimization approaches for feature selection. Neurocomputing 2016, 172, 371–381. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Kaveh, A.; Farhoudi, N. A new optimization method: Dolphin echolocation. Adv. Eng. Softw. 2013, 59, 53–70. [Google Scholar] [CrossRef]
- Hansen, N.; Müller, S.D.; Koumoutsakos, P. Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (CMA-ES). Evol. Comput. 2003, 11, 1–18. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Boschetti, M.A.; Maniezzo, V. Matheuristics: Using mathematics for heuristic design. 4OR 2022, 20, 173–208. [Google Scholar] [CrossRef]
- Omari, M.; Kaddi, M.; Salameh, K.; Alnoman, A.; Benhadji, M. Atomic Energy Optimization: A Novel Meta-Heuristic Inspired by Energy Dynamics and Dissipation. IEEE Access 2024, 13, 2801–2828. [Google Scholar] [CrossRef]
- Abdelhamid, A.A.; Towfek, S.K.; Khodadadi, N.; Alhussan, A.A.; Khafaga, D.S.; Eid, M.M.; Ibrahim, A. Waterwheel plant algorithm: A novel metaheuristic optimization method. Processes 2023, 11, 1502. [Google Scholar] [CrossRef]
- Rahman, A.; Sokkalingam, R.; Othman, M.; Biswas, K.; Abdullah, L.; Kadir, E.A. Nature-inspired metaheuristic techniques for combinatorial optimization problems: Overview and recent advances. Mathematics 2021, 9, 2633. [Google Scholar] [CrossRef]
- Agrawal, P.; Ganesh, T.; Mohamed, A.W. A novel binary gaining–sharing knowledge-based optimization algorithm for feature selection. Neural Comput. Appl. 2020, 33, 5989–6008. [Google Scholar] [CrossRef]
- Hosseini, S.; Al Khaled, A. A survey on the imperialist competitive algorithm metaheuristic: Implementation in engineering domain and directions for future research. Appl. Soft Comput. 2014, 24, 1078–1094. [Google Scholar] [CrossRef]
- Kuo, H.; Lin, C. Cultural evolution algorithm for global optimizations and its applications. J. Appl. Res. Technol. 2013, 11, 510–522. [Google Scholar] [CrossRef]
- Moghdani, R.; Salimifard, K. Volleyball premier league algorithm. Appl. Soft Comput. 2018, 64, 161–185. [Google Scholar] [CrossRef]
- Elmanakhly, D.A.; Saleh, M.; Rashed, E.A.; Abdel-Basset, M. BinHOA: Efficient binary horse herd optimization method for feature selection: Analysis and validations. IEEE Access 2022, 10, 26795–26816. [Google Scholar] [CrossRef]
- Rodrigues, D.; Pereira, L.A.; Almeida, T.N.S.; Papa, J.P.; Souza, A.N.; Ramos, C.C.; Yang, X.S. BCS: A binary cuckoo search algorithm for feature selection. In Proceedings of the 2013 IEEE International Symposium on Circuits and Systems (ISCAS), Beijing, China, 19–23 May 2013. [Google Scholar]
- Mafarja, M.M.; Eleyan, D.; Jaber, I.; Hammouri, A.; Mirjalili, S. Binary dragonfly algorithm for feature selection. In Proceedings of the 2017 International Conference on New Trends in Computing Sciences (ICTCS), Amman, Jordan, 11–13 October 2017. [Google Scholar]
- Rodrigues, D.; Yang, X.S.; De Souza, A.N.; Papa, J.P. Binary flower pollination algorithm and its application to feature selection. In Recent Advances in Swarm Intelligence and Evolutionary Computation; Springer International Publishing: Cham, Switzerland, 2015; pp. 85–100. [Google Scholar]
- Xue, B.; Zhang, M.; Browne, W.N. Particle swarm optimisation for feature selection in classification: Novel initialisation and updating mechanisms. Appl. Soft Comput. 2014, 18, 261–276. [Google Scholar] [CrossRef]
- Al-Tashi, Q.; Kadir, S.J.A.; Rais, H.M.; Mirjalili, S.; Alhussian, H. Binary optimization using hybrid grey wolf optimization for feature selection. IEEE Access 2019, 7, 39496–39508. [Google Scholar] [CrossRef]
- Shikoun, N.H.; Al-Eraqi, A.S.; Fathi, I.S. BinCOA: An Efficient Binary Crayfish Optimization Algorithm for Feature Selection. IEEE Access 2024, 12, 28621–28635. [Google Scholar] [CrossRef]
- Kumar, M.; Husain, D.M.; Upreti, N.; Gupta, D. Genetic Algorithm: Review and Application. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3529843 (accessed on 3 March 2020).
- Chen, H.; Jiang, W.; Li, C.; Li, R. A heuristic feature selection approach for text categorization by using chaos optimization and genetic algorithm. Math. Probl. Eng. 2013, 2013, 1–6. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, D.-W.; Gao, X.-Z.; Tian, T.; Sun, X.-Y. Binary differential evolution with self-learning for multi-objective feature selection. Inf. Sci. 2020, 507, 67–85. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-based optimization. In IEEE Transactions on Evolutionary Computation; IEEE: New York, NY, USA, 2008; Volume 12, pp. 702–713. [Google Scholar]
- Khalilpourazari, S.; Naderi, B.; Khalilpourazary, S. Multi-objective stochastic fractal search: A powerful algorithm for solving complex multi-objective optimization problems. Soft Comput. 2019, 24, 3037–3066. [Google Scholar] [CrossRef]
- Shareef, H.; Ibrahim, A.A.; Mutlag, A.H. Lightning search algorithm. Appl. Soft Comput. 2015, 36, 315–333. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2015, 27, 495–513. [Google Scholar] [CrossRef]
- Abedinpourshotorban, H.; Shamsuddin, S.M.; Beheshti, Z.; Jawawi, D.N. Electromagnetic field optimization: A physics-inspired metaheuristic optimization algorithm. Swarm Evol. Comput. 2016, 26, 8–22. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W.; Mirjalili, S. Henry gas solubility optimization: A novel physics-based algorithm. Futur. Gener. Comput. Syst. 2019, 101, 646–667. [Google Scholar] [CrossRef]
- Taradeh, M.; Mafarja, M.; Heidari, A.A.; Faris, H.; Aljarah, I.; Mirjalili, S.; Fujita, H. An evolutionary gravitational search-based feature selection. Inf. Sci. 2019, 497, 219–239. [Google Scholar] [CrossRef]
- Hosseini, F.S.; Choubin, B.; Mosavi, A.; Nabipour, N.; Shamshirband, S.; Darabi, H.; Haghighi, A.T. Flash-flood hazard assessment using ensembles and Bayesian-based machine learning models: Application of the simulated annealing feature selection method. Sci. Total. Environ. 2020, 711, 135161. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Ahmed, S.; Ghosh, K.K.; Mirjalili, S.; Sarkar, R. AIEOU: Automata-based improved equilibrium optimizer with U-shaped transfer function for feature selection. Knowl. Based Syst. 2021, 228, 107283. [Google Scholar] [CrossRef]
- Azizi, M.; Aickelin, U.; Khorshidi, H.A.; Shishehgarkhaneh, M.B. Energy valley optimizer: A novel metaheuristic algorithm for global and engineering optimization. Sci. Rep. 2023, 13, 226. [Google Scholar] [CrossRef]
- Deep, K.; Thakur, M. A new crossover operator for real coded genetic algorithms. Appl. Math. Comput. 2007, 188, 895–911. [Google Scholar] [CrossRef]
- Wang, F.; Chen, Y.; Liu, Y. Finite Difference and Chebyshev Collocation for Time-Fractional and Riesz Space Distributed-Order Advection–Diffusion Equation with Time-Delay. Fractal Fract. 2024, 8, 700. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Alsuyuti, M.M. Numerical treatment of multi-term fractional differential equations via new kind of generalized Chebyshev polynomials. Fractal Fract. 2023, 7, 74. [Google Scholar] [CrossRef]
- Bao, H.; Liang, G.; Cai, Z.; Chen, H. Random replacement crisscross butterfly optimization algorithm for standard evaluation of overseas Chinese associations. Electronics 2022, 11, 1080. [Google Scholar] [CrossRef]
- Pernkopf, F. Bayesian network classifiers versus selective k-NN classifier. Pattern Recognit. 2005, 38, 1–10. [Google Scholar] [CrossRef]
- Zhu, Z.; Ong, Y.S.; Dash, M. Wrapper–filter feature selection algorithm using a memetic framework. IEEE Trans. Syst. Man Cybern. Part B 2007, 37, 70–76. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Song, Q.; Xi, M.; Zhou, Z. Binary arithmetic optimization algorithm for feature selection. Soft Comput. 2023, 27, 11395–11429. [Google Scholar] [CrossRef]
- Chopra, N.; Ansari, M.M. Golden jackal optimization: A novel nature-inspired optimizer for engineering applications. Expert Syst. Appl. 2022, 198, 116924. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Mirjalili, S. Artificial hummingbird algorithm: A new bio-inspired optimizer with its engineering applications. Comput. Methods Appl. Mech. Eng. 2022, 388, 114194. [Google Scholar] [CrossRef]
- Seyyedabbasi, A. Binary sand cat swarm optimization algorithm for wrapper feature selection on biological data. Biomimetics 2023, 8, 310. [Google Scholar] [CrossRef] [PubMed]
- Chauhan, D.; Yadav, A. Binary artificial electric field algorithm. Evol. Intell. 2022, 16, 1155–1183. [Google Scholar] [CrossRef]
- Kudela, J. The evolutionary computation methods no one should use. arXiv 2023, arXiv:2301.01984. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).