Existence of Positive Solutions for a Class of Nabla Fractional Difference Equations with Parameter-Dependent Summation Boundary Conditions

Abstract

In this manuscript, we study a class of nabla fractional difference equations with summation boundary conditions that depend on a parameter. We construct the Green’s function related to the linear problem and we deduce some of its properties. First, we obtain an upper bound of the sum of it, and use this property to give an existence result for the considered problem based on the Leray–Shauder nonlinear alternative. Then, we establish some bounds on the parameter in which the Green’s function is positive, and by using Krasnoselski–Zabreiko fixed-point theorem, we deduce another existence result. Finally, we give some particular examples in order to demonstrate our primary findings.

1. Introduction

Discrete fractional calculus is a branch of mathematical analysis that extends the concepts of continuous fractional calculus to discrete systems. While traditional fractional calculus deals with derivatives and integrals of noninteger order in continuous domains, discrete fractional ones focus on similar operations but within discrete sequences. This field finds applications in numerous branches of engineering and science including signal processing, control theory, and mathematical modeling of phenomena in economics, biology, and physics, where discrete events or data points are predominant. We refer to the reader [1,2,3,4] and the references therein for a detailed introduction to discrete fractional calculus.

In the last few decades, interest in discrete fractional problems has surged [5,6,7,8]. Consequently, many articles on this topic appeared for both delta problems and nabla problems with Liouville–Caputo [9,10,11,12] or Riemann–Liouville operators [13,14,15,16,17] under different boundary conditions. For example, in a very recent paper [18], the authors managed to ensure the existence results for the problem

$$\begin{array}{c}-\left({\nabla }_{d_1-1}^{\nu }w\right)\left(\zeta \right)=\lambda f\left(\zeta \right)g\left(w\left(\zeta \right)\right),\zeta \in {\mathbb{N}}_{d_1+2}^{d_2},\\ w\left(d_1\right)=\left({\nabla }_{d_1-1}^{\mu }w\right)\left(d_2\right)=0,\end{array}$$

where $f:{\mathbb{N}}_{d_1+2}^{d_2}\to (0,\infty )$ and $g:[0,\infty )\to [0,\infty )$ are continuous functions; $0\le \mu \le 1<\nu <2$; ${\nabla }_{d_1-1}^{\nu }$ and ${\nabla }_{d_1-1}^{\mu }$ are $\nu$-thand $\mu$-th order nabla difference operators.

Since many mathematical models in different areas of science and engineering [19,20,21,22] such as elasticity, electric railway systems, electric power networks, telecommunication lines, thermodynamics and others can be represented as multi-point boundary value problems, the interest in analyzing such discrete delta fractional problems increased lately.

In one of the first notable works [23], considering delta fractional problem with summation conditions

$$\begin{array}{c}{\mathrm{\Delta }}^{\eta }w\left(\zeta \right)=\mathfrak{f}(\zeta +\eta -1,w(\zeta +\eta -1),\mathrm{\Delta }w(\zeta +\eta -1)),1<\eta \le 2,\zeta \in {\mathbb{N}}_0^{l+2},\\ w(\eta -2)=0,w(\zeta +l+1)=\sum _{s=\eta -1}^{\alpha }w\left(s\right),\alpha \in {[\eta -1,\eta +l]}_{{\mathbb{N}}_{\eta -1}},\end{array}$$

with $\mathfrak{f}:{\mathbb{R}}_{\eta -1}^{\eta +l+1}\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$, the authors deduced existence results using fixed-point theory. Later, these results were extended in [24].

However, for nabla fractional problems, such results are almost missing. In particular, there are many recent papers that deal with nabla problems with Dirichlet, periodic, anti-periodic, mixed or separated boundary conditions [25,26,27,28]; however, to the best of our knowledge, there is only one result regarding the nabla problem with summation conditions. Recently, in [29], the following nabla problem:

$$\begin{array}{c}-\left({\nabla }_{k-1}^{\eta }w\right)\left(\zeta \right)=\mathfrak{f}\left(\zeta ,w(\zeta \right)),1<\eta \le 2,\zeta \in {\mathbb{N}}_{k+2}^l,\\ w\left(k\right)=C,w\left(l\right)+\mu \sum _{s=k+1}^{l-1}w\left(s\right)=D,\mu >0,\end{array}$$

with $\mathfrak{f}:{\mathbb{R}}_{k+2}^l\times \mathbb{R}\to \mathbb{R}$ being continuous with respect to its second argument, was studied and the authors managed to obtain existence, uniqueness, and stability results. This was the first result regarding a nabla fractional problem with summation conditions. We point out that no results regarding the sign of the Green’s function were obtained and the authors of the above work only managed to obtain the existence of a sign-changing solution based on the fact that the related Green’s function there was also sign-changing.

Motivated by the works mentioned above, in this manuscript, we continue this research as we consider the following nabla problem:

$$\begin{array}{c}-\left({\nabla }_{k-1}^{\eta }w\right)\left(\zeta \right)=\mathfrak{f}\left(\zeta ,w(\zeta \right)),1<\eta \le 2,\zeta \in {\mathbb{N}}_{k+2}^l,\end{array}$$

(1)

$$\begin{array}{c}w\left(k\right)=0,w\left(l\right)=\mu \sum _{s=k+1}^{d}w\left(s\right),d\in {\mathbb{N}}_{k+1}^{l-1},\mu >0,\end{array}$$

(2)

where $\mathfrak{f}:{\mathbb{N}}_{k+2}^l\times \mathbb{R}\to \mathbb{R}$ is a continuous function.

The manuscript is organized as follows. In Section 2, we recall some preliminaries on nabla fractional calculus. In Section 3, we deduce the exact expression of the Green’s function that is associated with (1) and (2), and also derive some of its properties. After that, in Section 4, under some sufficient conditions, we obtain existence results for (1) and (2) using the Leray–Shauder nonlinear alternative. In Section 5, we establish some bounds on the parameter $\mu$ in which the related Green’s function is positive. Then, by using the Krasnoselski–Zabreiko fixed-point theorem, we obtain another type of existence result and, most importantly, for the first time in the literature, we deduce the existence of a strictly positive solution for (1) and (2). Finally, we illustrate our main findings in Section 6, as we provide a few examples there. In the end of this paper, in the Conclusion section, we give some ideas for possible future work in this direction.

In the existing literature on fractional problems with summation boundary conditions recently given in [29], the authors were only able to establish an upper bound of the Green’s function, which can be sign-changing and this only allowed them to deduce the existence of a solution that might be sign-changing as well. However, in this research, we introduced the new idea of finding an interval of the parameter $\mu$, where the Green’s function is strictly positive, which allowed us to prove the existence of strictly positive solutions. This is the main novelty in this work, which is a very important task in terms of better understanding the analytical side of these kinds of problems and their applications in the real world. This result has a clear physical interpretation since Green’s function can represent various physical properties. For example, in heat conduction problems, the Green’s function might depend on the temperature. For certain temperature ranges, the system might have a stable heat distribution, while outside of this range, some thermal runaway might occur. In electrical problems, parameters like conductivity, for instance, may affect the Green’s function. The positivity of it on a specific interval could indicate that the system is stable, while outside of this interval it might be unstable.

The only limitation of our work is that we were able to obtain the positivity of the Green’s function only in a given interval of the parameter $\mu$, but we think that a better result could not be obtained for such a general fractional problem with summation boundary conditions. However, we point out that these new results and novel ideas can be used in future works with the idea of obtaining a multiplicity of positive solutions for the considered problem (1) and (2) or other nabla problems with summation boundary conditions.

In terms of the novel contributions of this work, we highlight the following:

• The boundary value problems (1) and (2) considered in this work are completely new to the existing literature.
• The exact expression of the Green’s function associated with (1) and (2) is deduced, and the upper bound of its sum is obtained.
• We establish existence results for (1) and (2) under some sufficient conditions.
• We obtain an interval of the parameter in which the related Green’s function is strictly positive.
• Suitable conditions are imposed under which the problem considered (1) and (2) has at least one positive solution.

2. Preliminaries

For this work, we shall use the following fundamentals of discrete fractional calculus [3]. Denote by ${\mathbb{N}}_e=\{e,e+1,e+2,\dots \}$ and ${\mathbb{N}}_e^f=\{e,e+1,e+2,\dots ,f\}$ for any real e and f such that $f-e\in {\mathbb{N}}_1$. First, we recall some definitions and lemmas that will be used in this work.

Definition 1

([3]). For any a, $b\in \mathbb{R}$, the generalized rising function is

$$a^{\overline{b}}={\displaystyle \frac{\mathrm{\Gamma }(a+b)}{\mathrm{\Gamma }\left(a\right)}},$$

provided the quotient is well defined with $\mathrm{\Gamma }(·)$ being the Euler gamma function.

Definition 2

([3]). Let $\beta \in \mathbb{R}\setminus \{\dots ,-2,-1\}$. The βth-order nabla fractional Taylor monomial is

$${\mathfrak{H}}_{\beta }(\zeta ,k)={\displaystyle \frac{{(\zeta -k)}^{\overline{\beta }}}{\mathrm{\Gamma }(\beta +1)}},$$

provided on the right-hand side is well defined.

Definition 3

([3]). Let $w:{\mathbb{N}}_k\to \mathbb{R}$ and $N\in {\mathbb{N}}_1$. The first-order nabla difference of w is defined by

$$\left(\nabla w\right)\left(\zeta \right)=w\left(\zeta \right)-w(\zeta -1),\zeta \in {\mathbb{N}}_{k+1},$$

and the $Nth$-order nabla difference of w is defined recursively by

$$\left({\nabla }^{N}w\right)\left(\zeta \right)=\left(\nabla \left({\nabla }^{N-1}w\right)\right)\left(\zeta \right),\zeta \in {\mathbb{N}}_{k+N}.$$

We collect some important properties of nabla fractional Taylor monomials in the following lemmas.

Lemma 1

([3,11]). Let $s\in {\mathbb{N}}_k$ and $\mu >-1$. The following properties hold:

(a)

${\mathfrak{H}}_{\mu }(\zeta ,s-1)\ge 0$ for $\zeta \in {\mathbb{N}}_{s-1}$ and ${\mathfrak{H}}_{\mu }(\zeta ,s-1)>0$ for $\zeta \in {\mathbb{N}}_s$;

(b)

${\mathfrak{H}}_{\mu }(\zeta ,s-1)$ is a decreasing function of s for $\zeta \in {\mathbb{N}}_{s-1}$ and $\mu >0$. Moreover, it is an increasing function of ζ for $\zeta \in {\mathbb{N}}_s$ and $\mu >0$;

(c)

${\displaystyle {\mathfrak{H}}_{\mu }(\zeta ,k)-{\mathfrak{H}}_{\mu -1}(\zeta ,k)={\mathfrak{H}}_{\mu }(\zeta ,k+1)}$;

(d)

${\displaystyle \nabla {\mathfrak{H}}_{\mu }(l,\zeta )=-{\mathfrak{H}}_{\mu -1}(l+1,\zeta )}$;

(e)

${\displaystyle \sum _{s=k+1}^{\zeta }{\mathfrak{H}}_{\mu }(\zeta ,s-1)={\mathfrak{H}}_{\mu +1}(\zeta ,k)}$.

Lemma 2

([14]). Let $\mu >0$, $s\in {\mathbb{N}}_k$ and $\zeta \in {\mathbb{N}}_s$. Denote by

$${\mathfrak{h}}_{\mu }(\zeta ,s)={\displaystyle \frac{{\mathfrak{H}}_{\mu }(\zeta ,s-1)}{{\mathfrak{H}}_{\mu }(\zeta ,k-1)}}>0.$$

We have that ${\mathfrak{h}}_{\mu }(\zeta ,s)$ is a nondecreasing function of ζ for $\mu >0$.

Definition 4

([3]). Let $w:{\mathbb{N}}_{k+1}\to \mathbb{R}$ and $\eta >0$. The $\eta \mathrm{th}$-order nabla fractional sum of w based at k is

$$\left({\nabla }_k^{-\eta }w\right)\left(\zeta \right)=\sum _{s=k+1}^{\zeta }{\mathfrak{H}}_{\eta -1}(\zeta ,s-1)w\left(s\right),\zeta \in {\mathbb{N}}_k,$$

where by convention $\left({\nabla }_k^{-\eta }w\right)\left(k\right)=0$.

Definition 5

([3]). Let $w:{\mathbb{N}}_{k+1}\to \mathbb{R}$, $\eta >0$ and choose $N\in {\mathbb{N}}_1$ such that $N-1<\eta \le N$. The $\eta th$-order Riemann–Liouville nabla fractional difference of w based at k is

$$\left({\nabla }_k^{\eta }w\right)\left(\zeta \right)=\left({\nabla }^N\left({\nabla }_k^{-(N-\eta )}w\right)\right)\left(\zeta \right),\zeta \in {\mathbb{N}}_{k+N}.$$

Theorem 1

([14]). Assume $1<\eta \le 2$. The general solution of the nabla problem

$$\left({\nabla }_{k-1}^{\eta }w\right)\left(\zeta \right)=h\left(\zeta \right),\zeta \in {\mathbb{N}}_{k+2},$$

(3)

is

$$w\left(\zeta \right)=C_1{\mathfrak{H}}_{\eta -1}(\zeta ,k-1)+C_2{\mathfrak{H}}_{\eta -2}(\zeta ,k-1)+\sum _{s=k+2}^{\zeta }{\mathfrak{H}}_{\eta -1}(\zeta ,s-1)h\left(s\right),\zeta \in {\mathbb{N}}_k,$$

(4)

where $h:{\mathbb{N}}_{k+2}\to \mathbb{R}$.

3. Construction of Green’s Function

Here, we show how one can deduce the Green’s function that is related to the linear problem

$$\begin{array}{c}-\left({\nabla }_{k-1}^{\eta }w\right)\left(\zeta \right)=h\left(\zeta \right),1<\eta \le 2,\zeta \in {\mathbb{N}}_{k+2}^l,\end{array}$$

(5)

$$\begin{array}{c}w\left(k\right)=0,w\left(l\right)=\mu \sum _{s=k+1}^{d}w\left(s\right),d\in {\mathbb{N}}_{k+1}^{l-1},\mu >0.\end{array}$$

(6)

Here $h:{\mathbb{N}}_{k+2}^l\to \mathbb{R}$. Set

$$\mathrm{\Xi }={\mathfrak{H}}_{\eta -1}(l,k)-\mu {\mathfrak{H}}_{\eta }(d,k).$$

Theorem 2.

Let $\mathrm{\Xi }\ne 0$. The above linear problem (5) and (6) has a unique solution which is given as

$$w\left(\zeta \right)=\sum _{s=k+2}^l\mathcal{G}(\zeta ,s)h\left(s\right),\zeta \in {\mathbb{N}}_k^l,$$

(7)

where

$$\mathcal{G}(\zeta ,s)=\left\{\begin{array}{c}{\mathcal{G}}_1(\zeta ,s),s\le min\{\zeta ,d\},\hfill \\ {\mathcal{G}}_2(\zeta ,s),\zeta +1\le s\le d,\hfill \\ {\mathcal{G}}_3(\zeta ,s),d+1\le s\le \zeta ,\hfill \\ {\mathcal{G}}_4(\zeta ,s),s\ge max\{\zeta +1,d+1\},\hfill \end{array}\right.$$

with

$${\mathcal{G}}_1(\zeta ,s)={\displaystyle \frac{{\mathfrak{H}}_{\eta -1}(\zeta ,k){\mathfrak{H}}_{\eta -1}(l,s-1)}{\mathrm{\Xi }}}-{\displaystyle \frac{\mu {\mathfrak{H}}_{\eta -1}(\zeta ,k){\mathfrak{H}}_{\eta }(d,s-1)}{\mathrm{\Xi }}}-{\mathfrak{H}}_{\eta -1}(\zeta ,s-1),$$

$${\mathcal{G}}_2(\zeta ,s)={\displaystyle \frac{{\mathfrak{H}}_{\eta -1}(\zeta ,k){\mathfrak{H}}_{\eta -1}(l,s-1)}{\mathrm{\Xi }}}-{\displaystyle \frac{\mu {\mathfrak{H}}_{\eta -1}(\zeta ,k){\mathfrak{H}}_{\eta }(d,s-1)}{\mathrm{\Xi }}},$$

$${\mathcal{G}}_3(\zeta ,s)={\displaystyle \frac{{\mathfrak{H}}_{\eta -1}(\zeta ,k){\mathfrak{H}}_{\eta -1}(l,s-1)}{\mathrm{\Xi }}}-{\mathfrak{H}}_{\eta -1}(\zeta ,s-1),$$

and

$${\mathcal{G}}_4(\zeta ,s)={\displaystyle \frac{{\mathfrak{H}}_{\eta -1}(\zeta ,k){\mathfrak{H}}_{\eta -1}(l,s-1)}{\mathrm{\Xi }}}.$$

Proof. 

From (4) and $w\left(k\right)=0$, we get

$$C_1+C_2=0.$$

(8)

Next, from ${\displaystyle w\left(l\right)=\mu \sum _{s=k+1}^{d}w\left(s\right)}$, we obtain

$$\begin{array}{c}{C}_1{\mathfrak{H}}_{\eta -1}(l,k-1)+C_2{\mathfrak{H}}_{\eta -2}(l,k-1)-\sum _{s=k+2}^l{\mathfrak{H}}_{\eta -1}(l,s-1)h\left(s\right)\hfill \\ \hfill \hspace{1em}=\mu \sum _{s=k+1}^d\left[C_1{\mathfrak{H}}_{\eta -1}(s,k-1)+C_2{\mathfrak{H}}_{\eta -2}(s,k-1)-\sum _{r=k+2}^s{\mathfrak{H}}_{\eta -1}(s,r-1)h\left(r\right)\right].\end{array}$$

(9)

From (8) and (9) and Lemma 1(e), we have

$$C_1={\displaystyle \frac{1}{\mathrm{\Xi }}}\left[\sum _{s=k+2}^l{\mathfrak{H}}_{\eta -1}(l,s-1)h\left(s\right)-\mu \sum _{s=k+2}^d{\mathfrak{H}}_{\eta }(d,s-1)h\left(s\right)\right],$$

(10)

and

$$C_2=-{\displaystyle \frac{1}{\mathrm{\Xi }}}\left[\sum _{s=k+2}^l{\mathfrak{H}}_{\eta -1}(l,s-1)h\left(s\right)-\mu \sum _{s=k+2}^d{\mathfrak{H}}_{\eta }(d,s-1)h\left(s\right)\right].$$

(11)

Substituting (10) and (11) in (4), we have that

$$\begin{array}{ccc}\hfill w\left(\zeta \right)& =& {\displaystyle \frac{1}{\mathrm{\Xi }}}\left[\sum _{s=k+2}^l{\mathfrak{H}}_{\eta -1}(l,s-1)h\left(s\right)-\mu \sum _{s=k+2}^d{\mathfrak{H}}_{\eta }(d,s-1)h\left(s\right)\right]{\mathfrak{H}}_{\eta -1}(\zeta ,k-1)\hfill \\ & & -{\displaystyle \frac{1}{\mathrm{\Xi }}}\left[\sum _{s=k+2}^l{\mathfrak{H}}_{\eta -1}(l,s-1)h\left(s\right)-\mu \sum _{s=k+2}^d{\mathfrak{H}}_{\eta }(d,s-1)h\left(s\right)\right]{\mathfrak{H}}_{\eta -2}(\zeta ,k-1)\hfill \\ & & -\sum _{s=k+2}^{\zeta }{\mathfrak{H}}_{\eta -1}(\zeta ,s-1)h\left(s\right),\hfill \end{array}$$

which, using Lemma 1(c), can be written as

$$\begin{array}{ccc}\hfill w\left(\zeta \right)& =& {\displaystyle \frac{\left({\mathfrak{H}}_{\eta -1}(\zeta ,k-1)-{\mathfrak{H}}_{\eta -2}(\zeta ,k-1)\right)}{\mathrm{\Xi }}}\sum _{s=k+2}^l{\mathfrak{H}}_{\eta -1}(l,s-1)h\left(s\right)\hfill \\ \hfill & & -{\displaystyle \frac{\mu \left({\mathfrak{H}}_{\eta -1}(\zeta ,k-1)-{\mathfrak{H}}_{\eta -2}(\zeta ,k-1)\right)}{\mathrm{\Xi }}}\sum _{s=k+2}^d{\mathfrak{H}}_{\eta }(d,s-1)h\left(s\right)\hfill \\ \hfill & & -\sum _{s=k+2}^{\zeta }{\mathfrak{H}}_{\eta -1}(\zeta ,s-1)h\left(s\right)\hfill \\ \hfill & =& {\displaystyle \frac{{\mathfrak{H}}_{\eta -1}(\zeta ,k)}{\mathrm{\Xi }}}\sum _{s=k+2}^l{\mathfrak{H}}_{\eta -1}(l,s-1)h\left(s\right)-{\displaystyle \frac{\mu {\mathfrak{H}}_{\eta -1}(\zeta ,k)}{\mathrm{\Xi }}}\sum _{s=k+2}^d{\mathfrak{H}}_{\eta }(d,s-1)h\left(s\right)\hfill \\ & & -\sum _{s=k+2}^{\zeta }{\mathfrak{H}}_{\eta -1}(\zeta ,s-1)h\left(s\right)\hfill \\ \hfill & =& \sum _{s=k+2}^l\mathcal{G}(\zeta ,s)h\left(s\right).\hfill \end{array}$$

(12)

□

Lemma 3.

The Green’s function $\mathcal{G}(\zeta ,s)$ is such that

$$\underset{\zeta \in {\mathbb{N}}_k^l}{max}\sum _{s=k+2}^l\left|\mathcal{G}\left(\zeta ,s\right)\right|\le \mathrm{{\rm Y}},$$

(13)

where

$$\mathrm{{\rm Y}}={\displaystyle \frac{{\mathfrak{H}}_{\eta -1}(l,k){\mathfrak{H}}_{\eta }(l,k+1)}{\left|\mathrm{\Xi }\right|}}+{\displaystyle \frac{\mu {\mathfrak{H}}_{\eta -1}(l,k){\mathfrak{H}}_{\eta +1}(d,k+1)}{\left|\mathrm{\Xi }\right|}}+{\mathfrak{H}}_{\eta }(l,k+1).$$

Proof. 

Using similar arguments as before, from (12), we obtain

$$\begin{array}{cc}\hfill \sum _{s=k+2}^l\left|\mathcal{G}\left(\zeta ,s\right)\right|& \le {\displaystyle \frac{{\mathfrak{H}}_{\eta -1}(\zeta ,k)}{\left|\mathrm{\Xi }\right|}}\sum _{s=k+2}^l{\mathfrak{H}}_{\eta -1}(l,s-1)+{\displaystyle \frac{\mu {\mathfrak{H}}_{\eta -1}(\zeta ,k)}{\left|\mathrm{\Xi }\right|}}\sum _{s=k+2}^d{\mathfrak{H}}_{\eta }(d,s-1)\hfill \\ & +\sum _{s=k+2}^{\zeta }{\mathfrak{H}}_{\eta -1}(\zeta ,s-1)\hfill \\ & ={\displaystyle \frac{{\mathfrak{H}}_{\eta -1}(\zeta ,k){\mathfrak{H}}_{\eta }(l,k+1)}{\left|\mathrm{\Xi }\right|}}+{\displaystyle \frac{\mu {\mathfrak{H}}_{\eta -1}(\zeta ,k){\mathfrak{H}}_{\eta +1}(d,k+1)}{\left|\mathrm{\Xi }\right|}}\hfill \\ & +{\mathfrak{H}}_{\eta }(\zeta ,k+1)\left(\mathrm{By}\mathrm{Lemma}1\left(\mathrm{e}\right)\right)\hfill \\ & \le {\displaystyle \frac{{\mathfrak{H}}_{\eta -1}(l,k){\mathfrak{H}}_{\eta }(l,k+1)}{\left|\mathrm{\Xi }\right|}}+{\displaystyle \frac{\mu {\mathfrak{H}}_{\eta -1}(l,k){\mathfrak{H}}_{\eta +1}(d,k+1)}{\left|\mathrm{\Xi }\right|}}\hfill \\ & +{\mathfrak{H}}_{\eta }(l,k+1).\left(\mathrm{By}\mathrm{Lemma}1(\mathrm{b}\right))\hfill \end{array}$$

□

4. Existence Results

Here, we will give some existence results of (1) and (2) using the Leray–Schauder’s nonlinear alternative. Theorem 2 implies the equivalence between the solutions of (1) and (2) and

$$w\left(\zeta \right)=\sum _{s=k+2}^l\mathcal{G}(\zeta ,s)\mathfrak{f}(s,w\left(s\right)),\zeta \in {\mathbb{N}}_k^l.$$

Set $\mathcal{B}$ as the Banach space of all real-valued functions on ${\mathbb{N}}_k^l$ equipped with the maximum norm

$$∥y∥=\underset{\zeta \in {\mathbb{N}}_k^l}{max}\left|w\left(\zeta \right)\right|$$

for any $y\in \mathcal{B}$. Next, set the operator $S:\mathcal{B}\to \mathcal{B}$ by

$$\left(Sw\right)\left(\zeta \right)=\sum _{s=k+2}^l\mathcal{G}(\zeta ,s)\mathfrak{f}(s,w\left(s\right)),\zeta \in {\mathbb{N}}_k^l.$$

Clearly, w is a fixed point of S if and only if w is a solution of (1) and (2). For $r>0$ denote

$$K=\left\{u\in \mathcal{B}:u\left(k\right)=0,u\left(l\right)=\mu \sum _{s=k+1}^{d}u\left(s\right),d\in {\mathbb{N}}_{k+1}^{l-1},\mu >0,∥u∥\le r\right\}.$$

Throughout this section, we assume that $\mathrm{\Xi }\ne 0$. We use the following Leray–Schauder’s nonlinear alternative to study (1) and (2).

Theorem 3

([30]). (Leray–Schauder Nonlinear Alternative) Let $\mathcal{B}=\left(\mathcal{B},\parallel ·\parallel \right)$ be a Banach space, C be a closed, convex subset of $\mathcal{B}$, U an open subset of C and $0\in U$. Suppose that $T:\overline{U}\to C$ is a completely continuous map. Then, either

1.

T has a fixed point in $\overline{U}$;

2.

Or there exists a $y\in \partial U$ and $\lambda \in (0,1)$ such that $y=\lambda Ty$.

Theorem 4.

Suppose that

(C1) 

There exists $p:{\mathbb{N}}_{k+2}^l\to [0,\infty )$ and a nondecreasing function $q:[0,\infty )\to [0,\infty )$ such that

$$\left|\mathfrak{f}(\zeta ,y)\right|\le p\left(\zeta \right)q\left(\parallel y\parallel \right),(\zeta ,y)\in {\mathbb{N}}_{k+2}^l\times \mathbb{R}.$$

(C2) 

There exists $N>0$ such that

$${\displaystyle \frac{N}{\mathrm{{\rm Y}}\mathrm{\Omega }q\left(N\right)}}>1,$$

where

$$\mathrm{\Omega }=\underset{\zeta \in {\mathbb{N}}_{k+2}^l}{max}p\left(\zeta \right).$$

Then, problem (1) and (2) have a solution in K.

Proof. 

In the beginning, we claim that S maps bounded sets into bounded sets. Indeed, by (C1) and (13), for $\zeta \in {\mathbb{N}}_k^l$ and $w\in K$,

$$\begin{array}{cc}\hfill \left|\left(Sw\right)\left(\zeta \right)\right|& =\left|\sum _{s=k+2}^l\mathcal{G}(\zeta ,s)\mathfrak{f}(s,w\left(s\right))\right|\hfill \\ & \le \sum _{s=k+2}^l\left|\mathcal{G}(\zeta ,s)\right|\left|\mathfrak{f}(s,w(s\left)\right)\right|\hfill \\ & \le \sum _{s=k+2}^l\left|\mathcal{G}(\zeta ,s)\right|p\left(s\right)q\left(\left|w\right(s\left)\right|\right)\hfill \\ & \le q\left(\parallel w\parallel \right)\sum _{s=k+2}^l\left|\mathcal{G}(\zeta ,s)\right|p\left(s\right)\hfill \\ & \le \mathrm{{\rm Y}}\mathrm{\Omega }q\left(r\right),\hfill \end{array}$$

implying that

$$∥Sw∥\le \mathrm{{\rm Y}}\mathrm{\Omega }q\left(r\right).$$

Since ${\mathbb{N}}_k^l$ is a discrete set, by the Arzela–Ascoli theorem, S is completely continuous. Assume that $w\in \mathcal{B}$ and for some $0<\lambda <1$, we have $w=\lambda Sw$. Then, for $\zeta \in {\mathbb{N}}_k^l$, and again by (C1) and (13),

$$\begin{array}{cc}\hfill \left|w\left(\zeta \right)\right|& =\left|\lambda \left(Sw\right)\left(\zeta \right)\right|\hfill \\ & \le \sum _{s=k+2}^l\left|\mathcal{G}(\zeta ,s)\right|\left|\mathfrak{f}(s,w(s\left)\right)\right|\hfill \\ & \le \sum _{s=k+2}^l\left|\mathcal{G}(\zeta ,s)\right|p\left(s\right)q\left(\left|w\right(s\left)\right|\right)\hfill \\ & \le q\left(\parallel w\parallel \right)\sum _{s=k+2}^l\left|\mathcal{G}(\zeta ,s)\right|p\left(s\right)\hfill \\ & \le \mathrm{{\rm Y}}\mathrm{\Omega }q\left(\parallel w\parallel \right),\hfill \end{array}$$

implying that

$${\displaystyle \frac{\parallel w\parallel }{\mathrm{{\rm Y}}\mathrm{\Omega }q\left(\parallel w\parallel \right)}}\le 1.$$

Since $\parallel w\parallel \ne N$ from (C2), if

$$U=\left\{u\in \mathcal{B}:\parallel w\parallel <N\right\},$$

then $S:\overline{U}\to \mathcal{B}$ is a completely continuous operator. From the choice of U, there is no $w\in \partial U$ such that $w=\lambda Sw$ for any $0<\lambda <1$. Theorem 3 implies that S has a fixed point $w_0\in \overline{U}$ which is a solution of (1) and (2). □

5. Positive Green’s Function

In this section, we will establish some bounds on the parameter $\mu$ in order to ensure the positivity of the Green’s function defined in Theorem 2. Then, by applying the Krasnoselskii–Zabreiko fixed point theorem, we will obtain the existence of nontrivial solutions to problem (1) and (2) and finally we will deduce the existence of strictly positive solutions. We start with the following technical result.

Lemma 4.

Assume

$${\displaystyle \frac{\eta -1}{d-k}}\le \mu <{\displaystyle \frac{\eta \mathrm{\Gamma }\left(d-k\right)\mathrm{\Gamma }\left(l-k+\eta -1\right)}{\mathrm{\Gamma }\left(l-k\right)\mathrm{\Gamma }\left(d-k+\eta \right)}}.$$

(14)

Denote by

$$\varphi \left(s\right)={\mathfrak{H}}_{\eta -1}(l,s-1)-\mu {\mathfrak{H}}_{\eta }(d,s-1),s\in {\mathbb{N}}_{k+1}^d.$$

Then, the function ϕ has the following properties:

(i)

$\varphi (k+1)=\mathrm{\Xi }>0$;

(ii)

ϕ is a positive nondecreasing function on ${\mathbb{N}}_{k+1}^d$.

Proof. 

To verify (i), one can check that

$$\mathrm{\Xi }={\mathfrak{H}}_{\eta -1}(l,k)-\mu {\mathfrak{H}}_{\eta }(d,k)>0$$

is equivalent to

$$\mu <{\displaystyle \frac{{\mathfrak{H}}_{\eta -1}(l,k)}{{\mathfrak{H}}_{\eta }(d,k)}}={\displaystyle \frac{\eta \mathrm{\Gamma }\left(d-k\right)\mathrm{\Gamma }\left(l-k+\eta -1\right)}{\mathrm{\Gamma }\left(l-k\right)\mathrm{\Gamma }\left(d-k+\eta \right)}}.$$

To show that (ii) holds, for $s\in {\mathbb{N}}_{k+2}^d$, we have

$$\begin{array}{cc}\hfill \left(\nabla \varphi \right)\left(s\right)& =-{\mathfrak{H}}_{\eta -2}(l+1,s-1)+\mu {\mathfrak{H}}_{\eta -1}(d+1,s-1)\left(\mathrm{By}\mathrm{Lemma}1\left(\mathrm{d}\right)\right)\hfill \\ & \ge -{\mathfrak{H}}_{\eta -2}(d+2,s-1)+\mu {\mathfrak{H}}_{\eta -1}(d+1,s-1)\left(\mathrm{By}\mathrm{Lemma}1\left(\mathrm{b}\right)\right)\hfill \\ & =-{\displaystyle \frac{\mathrm{\Gamma }(d-s+\eta +1)}{\mathrm{\Gamma }(\eta -1)\mathrm{\Gamma }(d-s+3)}}+\mu {\displaystyle \frac{\mathrm{\Gamma }(d-s+\eta +1)}{\mathrm{\Gamma }\left(\eta \right)\mathrm{\Gamma }(d-s+2)}}\hfill \\ & ={\displaystyle \frac{\mathrm{\Gamma }(d-s+\eta +1)}{\mathrm{\Gamma }(\eta -1)\mathrm{\Gamma }(d-s+2)}}\left[-{\displaystyle \frac{1}{d-s+2}}+\mu {\displaystyle \frac{1}{\eta -1}}\right]\hfill \\ & \ge {\displaystyle \frac{\mathrm{\Gamma }(d-s+\eta )}{\mathrm{\Gamma }(\eta -1)\mathrm{\Gamma }(d-s+2)}}\left[-{\displaystyle \frac{1}{d-k}}+\mu {\displaystyle \frac{1}{\eta -1}}\right]\ge 0,\hfill \end{array}$$

implying (ii). □

Lemma 5.

Assume (14) holds. We have

$$\mathcal{G}(\zeta ,s)\ge 0,(\zeta ,s)\in {\mathbb{N}}_k^l\times {\mathbb{N}}_{k+2}^l.$$

Proof. 

Clearly, from the expressions of the Green’s function $\mathcal{G}(\zeta ,s)$ and Lemma 1(a), ${\mathcal{G}}_1(\zeta ,s)\le {\mathcal{G}}_i(\zeta ,s)$ for $i=2,3,4$ and it is enough to show that ${\mathcal{G}}_1(\zeta ,s)\ge 0$.

Using Lemma 1(a) and Lemma 4, one can check that

$$\begin{array}{cc}\hfill {\mathcal{G}}_1(\zeta ,s)& ={\displaystyle \frac{{\mathfrak{H}}_{\eta -1}(\zeta ,k){\mathfrak{H}}_{\eta -1}(l,s-1)}{\mathrm{\Xi }}}-{\displaystyle \frac{\mu {\mathfrak{H}}_{\eta -1}(\zeta ,k){\mathfrak{H}}_{\eta }(d,s-1)}{\mathrm{\Xi }}}-{\mathfrak{H}}_{\eta -1}(\zeta ,s-1)\hfill \\ & ={\displaystyle \frac{1}{\mathrm{\Xi }}}[{\mathfrak{H}}_{\eta -1}(\zeta ,k)\varphi \left(s\right)-{\mathfrak{H}}_{\eta -1}(\zeta ,s-1)\varphi (k+1)]\hfill \\ & \ge {\displaystyle \frac{{\mathfrak{H}}_{\eta -1}(\zeta ,s-1)}{\mathrm{\Xi }}}[\varphi \left(s\right)-\varphi (k+1)]\hfill \\ & \ge 0.\hfill \end{array}$$

□

In the next two examples, we will numerically validate our main new result. We point out that, indeed, for $\mu$, satisfying (14), the Green’s function is positive, while outside of this interval, the Green’s function is negative.

Example 1.

Take $k=0$, $l=5$, $d=2$, $\eta =1.5$, $\mu =0.5$. Clearly,

$${\displaystyle \frac{\eta -1}{\eta }}\le \mu <{\displaystyle \frac{\eta \mathrm{\Gamma }\left(d-k\right)\mathrm{\Gamma }\left(l-k+\eta -1\right)}{\mathrm{\Gamma }\left(l-k\right)\mathrm{\Gamma }\left(d-k+\eta \right)}}.$$

The values of $\mathcal{G}(\zeta ,s)$ for $(\zeta ,s)\in {\mathbb{N}}_0^5\times {\mathbb{N}}_2^5$ are presented in

Table 1. Values of $\mathcal{G}(\zeta ,s)$.

•	$\mathit{\zeta }=0$	$\mathit{\zeta }=1$	$\mathit{\zeta }=2$	$\mathit{\zeta }=3$	$\mathit{\zeta }=4$	$\mathit{\zeta }=5$
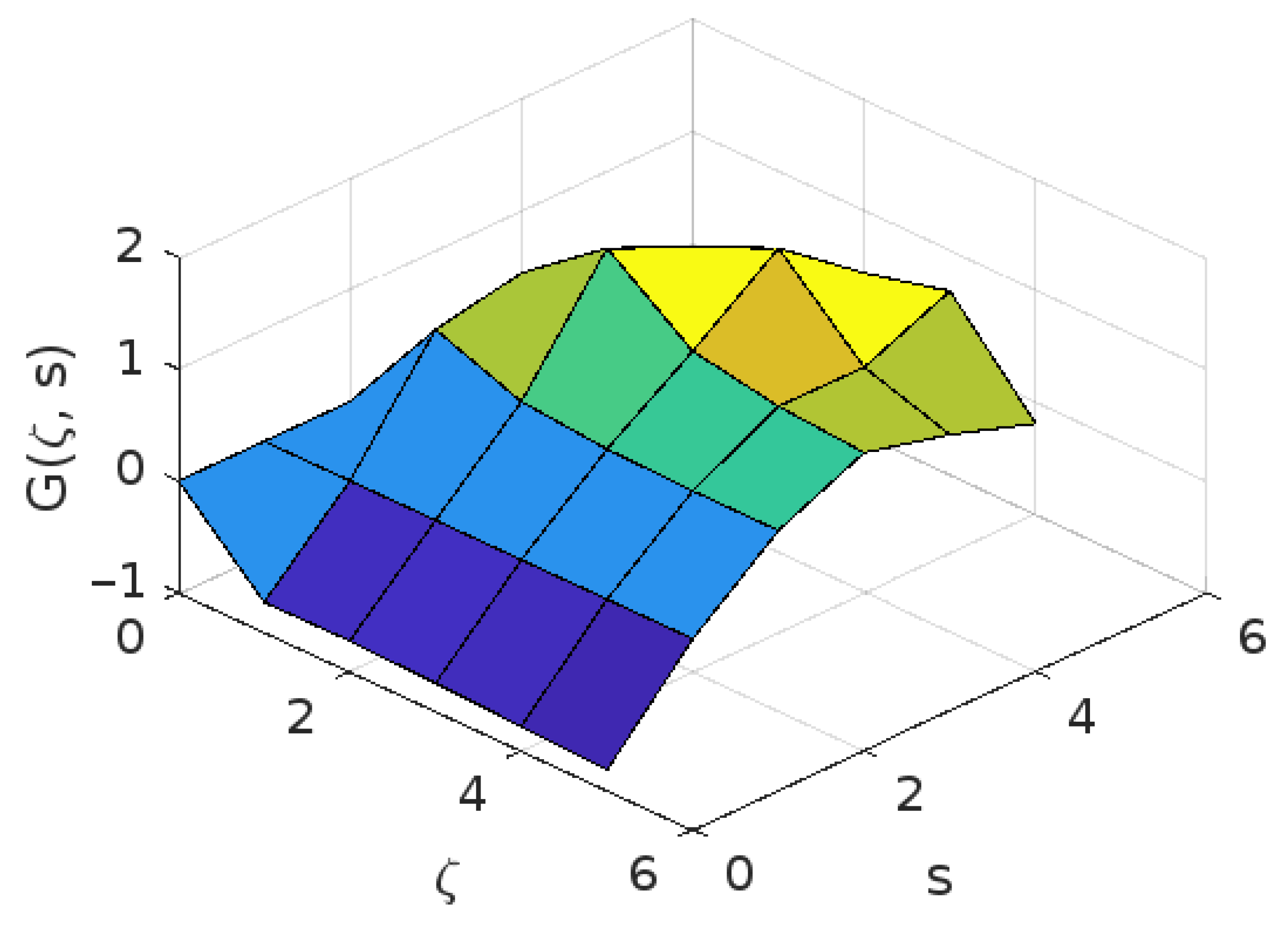
$s=2$	0	1.3936	1.0904	1.1130	1.1735	1.2420
$s=3$	0	1.5484	2.3227	1.9033	1.8872	1.9356
$s=4$	0	1.2387	1.8581	2.3227	1.7098	1.5485
$s=5$	0	0.8258	1.2387	1.5484	1.8065	1.0323

.

Example 2.

Take $k=0$, $l=5$, $d=2$, $\eta =1.5$, $\mu =1$. Clearly,

$${\displaystyle \frac{\eta \mathrm{\Gamma }\left(d-k\right)\mathrm{\Gamma }\left(l-k+\eta -1\right)}{\mathrm{\Gamma }\left(l-k\right)\mathrm{\Gamma }\left(d-k+\eta \right)}}<\mu .$$

The values of $\mathcal{G}(\zeta ,s)$ for $(\zeta ,s)\in {\mathbb{N}}_0^5\times {\mathbb{N}}_2^5$ are presented in

Table 2. Values of $\mathcal{G}(\zeta ,s)$.

•	$\mathit{\zeta }=0$	$\mathit{\zeta }=1$	$\mathit{\zeta }=2$	$\mathit{\zeta }=3$	$\mathit{\zeta }=4$	$\mathit{\zeta }=5$
$s=2$	0	−30.3708	−46.5563	−58.4453	−68.3112	−76.9282
$s=3$	0	−47.9540	−71.9309	−90.9137	−106.3993	−119.8867
$s=4$	0	−38.3632	−57.5448	−71.9309	−84.9194	−95.9094
$s=5$	0	−25.5754	−38.3632	−47.9540	−55.9463	−63.9396

.

Lemma 6.

Assume (14) holds. Then,

$$\underset{\zeta \in {\mathbb{N}}_k^l}{max}\sum _{s=k+2}^l\mathcal{G}\left(\zeta ,s\right)=g\left({\zeta }^{*}\right),$$

(15)

where

$$g\left(\zeta \right)={\displaystyle \frac{\left(\gamma \eta -\zeta +k+1\right)\mathrm{\Gamma }\left(\zeta +\eta -k-1\right)}{\mathrm{\Gamma }\left(\eta \right)\mathrm{\Gamma }\left(\zeta -k\right)}},\zeta \in {\mathbb{N}}_k^l,$$

and

$${\zeta }^{*}=\lfloor \gamma (\eta -1)+k+1\rfloor .$$

Here

$$\gamma ={\displaystyle \frac{{\mathfrak{H}}_{\eta }(l,k+1)-\mu \left({\mathfrak{H}}_{\eta +1}(d,k)-{\mathfrak{H}}_{\eta }(d,k)\right)}{\mathrm{\Xi }}}.$$

Proof. 

From Lemma 1(e),

$$\sum _{s=k+2}^{\zeta }{\mathfrak{H}}_{\eta -1}(\zeta ,s-1)={\mathfrak{H}}_{\eta }(\zeta ,k+1)$$

and

$$\sum _{s=k+2}^{\zeta }{\mathfrak{H}}_{\eta }(\zeta ,s-1)={\mathfrak{H}}_{\eta +1}(\zeta ,k)-{\mathfrak{H}}_{\eta }(\zeta ,k).$$

Now, from (12), we deduce that

$$\begin{array}{ccc}\hfill \sum _{s=k+2}^l\mathcal{G}\left(\zeta ,s\right)& =& {\displaystyle \frac{{\mathfrak{H}}_{\eta -1}(\zeta ,k)}{\mathrm{\Xi }}}{\mathfrak{H}}_{\eta }(l,k+1)-{\displaystyle \frac{\mu {\mathfrak{H}}_{\eta -1}(\zeta ,k)}{\mathrm{\Xi }}}\left({\mathfrak{H}}_{\eta +1}(d,k)-{\mathfrak{H}}_{\eta }(d,k)\right)\hfill \\ & & -{\mathfrak{H}}_{\eta }(\zeta ,k+1).\hfill \end{array}$$

Then,

$$\begin{array}{ccc}\hfill \sum _{s=k+2}^l\mathcal{G}\left(\zeta ,s\right)& =& \gamma {\mathfrak{H}}_{\eta -1}(\zeta ,k)-{\mathfrak{H}}_{\eta }(\zeta ,k+1)\hfill \\ & =& {\displaystyle \frac{\left(\gamma \eta -\zeta +k+1\right)\mathrm{\Gamma }\left(\zeta +\eta -k-1\right)}{\mathrm{\Gamma }\left(\eta \right)\mathrm{\Gamma }\left(\zeta -k\right)}}=g\left(\zeta \right).\hfill \end{array}$$

For $\zeta \in {\mathbb{N}}_{k+1}^l$, one can compute that

$$(\nabla g)\left(\zeta \right)={\displaystyle \frac{\mathrm{\Gamma }\left(\zeta +\eta -k-2\right)}{\mathrm{\Gamma }\left(\eta \right)\mathrm{\Gamma }\left(\zeta -k\right)}}\left(\gamma \eta -\gamma -\zeta +k+1\right).$$

Clearly, for $\zeta \in {\mathbb{N}}_{k+1}^l$ and $1<\eta <2$, $\mathrm{\Gamma }\left(\zeta +\eta -k-2\right)>0$, $\mathrm{\Gamma }\left(\eta \right)>0$ and $\mathrm{\Gamma }\left(\zeta -k\right)>0$. Then, equation $(\nabla g)\left(\zeta \right)=0$ has a unique solution $\gamma (\eta -1)+k+1$, so we set ${\zeta }^{*}$ as the critical point of g. If $\zeta \le {\zeta }^{*}$, the term $\left(\gamma \eta -\gamma -\zeta +k+1\right)$ is positive, and thus g is increasing. On the other hand, if $\zeta \ge {\zeta }^{*}$, the term $\left(\gamma \eta -\gamma -\zeta +k+1\right)$ is negative, and thus g is decreasing. Hence, the maximum value of g occurs at ${\zeta }^{*}$. Thus, we obtain (15). □

Let us recall the following Krasnoselskii–Zabreiko fixed point theorem [31].

Theorem 5.

Let X be a Banach space, and let $\mathfrak{f}:X\to X$ be a completely continuous operator. If there exists a bounded linear operator $A:X\to X$ such that 1 is not an eigenvalue and

$$\underset{∥y∥\to \infty }{lim}{\displaystyle \frac{∥\mathfrak{f}\left(y\right)-A\left(y\right)∥}{∥y∥}}=0,$$

then $\mathfrak{f}$ has a fixed point in $X.$

Finally, we establish our main result in this section following the idea given in [32].

Theorem 6.

Suppose that (14) holds. Moreover, if

$$\underset{\left|r\right|\to \infty }{lim}{\displaystyle \frac{\mathfrak{f}\left(\zeta ,r\right)}{r}}=m\left(\zeta \right)<{\displaystyle \frac{1}{g\left({\zeta }^{*}\right)}}\mathrm{for}\mathrm{all}\zeta \in {\mathbb{N}}_k^l,$$

(16)

then (1) and (2) has at least one solution $w.$ Furthermore, if $\mathfrak{f}\left(\zeta ,0\right)\ne 0$ for some $\zeta \in {\mathbb{N}}_k^l,$ then w is nontrivial, while if $\mathfrak{f}:{\mathbb{N}}_{k+2}^l\times (0,\infty )\to (0,\infty )$, then w is a positive solution.

Proof. 

Corresponding to (1) and (2), consider the problem

$$-\left({\nabla }_{k-1}^{\eta }w\right)\left(\zeta \right)=m\left(\zeta \right)w\left(\zeta \right),\zeta \in {\mathbb{N}}_{k+2}^l,$$

(17)

coupled with the boundary conditions (2) and define a completely continuous operator $A:\mathcal{B}\to \mathcal{B}$ by

$$\left(Aw\right)\left(\zeta \right)=\sum _{s=k+2}^l\mathcal{G}\left(\zeta ,s\right)m\left(s\right)w\left(s\right),\zeta \in {\mathbb{N}}_k^l.$$

It is clear that every solution of (17) and (2) is a fixed point of A, and conversely. First, we claim that 1 is not an eigenvalue of A. Indeed, since (17) and (2) has only the trivial solution $m\left(\zeta \right)=0$ for all $\zeta \in {\mathbb{N}}_k^l$, then it is clear that 1 is not an eigenvalue of A. On the other hand, if $m\left(\zeta \right)\ne 0$ for at least one $\zeta \in {\mathbb{N}}_k^l$, and (17) and (2) has a nontrivial solution w with $∥w∥>0.$ Moreover, using (15), we have that

$$∥w∥=∥Aw∥=\underset{\zeta \in {\mathbb{N}}_k^l}{max}\left|\sum _{s=k+2}^l\mathcal{G}\left(\zeta ,s\right)m\left(s\right)w\left(s\right)\right|<{\displaystyle \frac{∥w∥}{g\left({\zeta }^{*}\right)}}\underset{\zeta \in {\mathbb{N}}_k^l}{max}\sum _{s=k+2}^l\mathcal{G}\left(\zeta ,s\right)<∥w∥,$$

which means that again 1 is not an eigenvalue of $A.$

Now, we will show that

$$\underset{∥w∥\to \infty }{lim}{\displaystyle \frac{∥S\left(w\right)-A\left(w\right)∥}{∥w∥}}=0.$$

Let $ϵ>0$ be given. From (16), there exists $M\left(\zeta \right)>0$ such that for all $\left|r\right|>M\left(\zeta \right)$,

$$\left|\mathfrak{f}\left(\zeta ,r\right)-m\left(\zeta \right)\right|<ϵ\left|r\right|.$$

(18)

Denote

$$N_1=\underset{\zeta \in {\mathbb{N}}_k^l}{max}M\left(\zeta \right)>0,N=\underset{\left|r\right|\le N_1,\zeta \in {\mathbb{N}}_k^l}{max}\left|\mathfrak{f}\left(\zeta ,r\right)\right|>0,$$

and let $L\ge N_1$ be such that

$$N+{\displaystyle \frac{N_1}{g\left({\zeta }^{*}\right)}}<ϵL.$$

Next, choose $u\in \mathcal{B}$ with $∥w∥>L$. If $\left|w\left(s\right)\right|\le N_1$ for $s\in {\mathbb{N}}_k^l$, we have

$$\left|\mathfrak{f}\left(s,w\left(s\right)\right)-m\left(s\right)w\left(s\right)\right|\le \left|\mathfrak{f}\left(s,w\left(s\right)\right)\right|+{\displaystyle \frac{\left|w\left(s\right)\right|}{g\left({\zeta }^{*}\right)}}\le N+{\displaystyle \frac{N_1}{g\left({\zeta }^{*}\right)}}<ϵL<ϵ∥w∥.$$

If, on the other hand, $\left|w\left(s\right)\right|>N_1$, using (18), we deduce that

$$\left|\mathfrak{f}\left(s,w\left(s\right)\right)-m\left(s\right)w\left(s\right)\right|<ϵ\left|w\left(s\right)\right|\le ϵ∥w∥.$$

As a consequence, we have that

$$\left|\mathfrak{f}\left(s,w\left(s\right)\right)-m\left(s\right)w\left(s\right)\right|<ϵ∥w∥\mathrm{for}\mathrm{all}s\in {\mathbb{N}}_k^l.$$

Then, for $w\in \mathcal{B}$ with $∥w∥>L$,

$$\begin{array}{ccc}\hfill ∥S\left(w\right)-A\left(w\right)∥& =& \underset{\zeta \in {\mathbb{N}}_k^l}{max}\left|\sum _{s=k+2}^l\mathcal{G}\left(\zeta ,s\right)\left(\mathfrak{f}\left(s,w\left(s\right)\right)-m\left(s\right)w\left(s\right)\right)\right|\hfill \\ & \le & g\left({\zeta }^{*}\right)\left|\mathfrak{f}\left(s,w\left(s\right)\right)-m\left(s\right)w\left(s\right)\right|\hfill \\ & <& ϵ∥w∥g\left({\zeta }^{*}\right).\hfill \end{array}$$

Thus, we proved that

$$\underset{∥w∥\to \infty }{lim}{\displaystyle \frac{∥S\left(w\right)-A\left(w\right)∥}{∥w∥}}=0.$$

Therefore, by Theorem 5, S has a fixed point $w\in \mathcal{B}$ which is a nontrivial solution of (1) and (2) if $\mathfrak{f}\left(\zeta ,0\right)\ne 0$ for some $\zeta \in {\mathbb{N}}_{k+2}^l$. □

6. Examples

In the end, in this section, we give some examples that illustrate our main results of this manuscript.

Example 3.

Consider the problem

$$\left\{\begin{array}{c}\left({\nabla }_{-1}^{1.5}w\right)\left(\zeta \right)+\zeta w^2\left(\zeta \right)=0,\zeta \in {\mathbb{N}}_2^5,\hfill \\ w\left(0\right)=0,w\left(5\right)=w\left(1\right)+w\left(2\right).\hfill \end{array}\right.$$

(19)

Here $k=0$, $l=5$, $d=2$, $\eta =1.5$, $\mu =1$, and $\mathfrak{f}(\zeta ,r)=\zeta r^2$. Clearly,

$$\left|\mathfrak{f}(\zeta ,r)\right|\le p\left(\zeta \right)q\left(\left|r\right|\right),(\zeta ,r)\in {\mathbb{N}}_2^5\times \mathbb{R},$$

where

$$p\left(\zeta \right)=\zeta ,\zeta \in {\mathbb{N}}_2^5,$$

and

$$q\left(\left|r\right|\right)={\left|r\right|}^2=r^2,r\in \mathbb{R}.$$

In addition, $p:{\mathbb{N}}_2^5\to [0,\infty )$ and $q:[0,\infty )\to [0,\infty )$ are nondecreasing functions. Thus, assumption (C1) of Theorem 4 holds. Moreover,

$$\mathrm{\Omega }=\underset{\zeta \in {\mathbb{N}}_2^5}{max}p\left(\zeta \right)=5.$$

Now, we calculate Y. The Green’s function associated with (19) is given by

$$\mathcal{G}(\zeta ,s)=\left\{\begin{array}{c}{\mathcal{G}}_1(\zeta ,s),s\le min\{\zeta ,2\},\hfill \\ {\mathcal{G}}_2(\zeta ,s),\zeta +1\le s\le 2,\hfill \\ {\mathcal{G}}_3(\zeta ,s),3\le s\le \zeta ,\hfill \\ {\mathcal{G}}_4(\zeta ,s),s\ge max\{\zeta +1,3\},\hfill \end{array}\right.$$

with

$${\mathcal{G}}_1(\zeta ,s)=-{\displaystyle \frac{{\mathfrak{H}}_{0.5}(\zeta ,0){\mathfrak{H}}_{0.5}(5,s-1)}{0.0391}}+{\displaystyle \frac{{\mathfrak{H}}_{0.5}(\zeta ,0){\mathfrak{H}}_{1.5}(2,s-1)}{0.0391}}-{\mathfrak{H}}_{0.5}(\zeta ,s-1),$$

$${\mathcal{G}}_2(\zeta ,s)=-{\displaystyle \frac{{\mathfrak{H}}_{0.5}(\zeta ,0){\mathfrak{H}}_{0.5}(5,s-1)}{0.0391}}+{\displaystyle \frac{{\mathfrak{H}}_{0.5}(\zeta ,0){\mathfrak{H}}_{1.5}(2,s-1)}{0.0391}}$$

$${\mathcal{G}}_3(\zeta ,s)=-{\displaystyle \frac{{\mathfrak{H}}_{0.5}(\zeta ,0){\mathfrak{H}}_{0.5}(5,s-1)}{0.0391}}-{\mathfrak{H}}_{0.5}(\zeta ,s-1)$$

and

$${\mathcal{G}}_4(\zeta ,s)=-{\displaystyle \frac{{\mathfrak{H}}_{0.5}(\zeta ,0){\mathfrak{H}}_{0.5}(5,s-1)}{0.0391}}.$$

Then,

$$\mathrm{{\rm Y}}={\displaystyle \frac{{\mathfrak{H}}_{0.5}(5,0){\mathfrak{H}}_{1.5}(5,1)}{0.0391}}+{\displaystyle \frac{{\mathfrak{H}}_{0.5}(5,0){\mathfrak{H}}_{2.5}(2,1)}{0.0391}}+{\mathfrak{H}}_{1.5}(5,1)=482.5431.$$

There exists $0<N<{\displaystyle \frac{1}{2412}}$ such that (C2) of Theorem 4 holds. Therefore, by Theorem 3, (19) has a solution defined on ${\mathbb{N}}_0^5$. The values of $\mathcal{G}(\zeta ,s)$ are presented in

Table 3. Values of $\mathcal{G}(\zeta ,s)$.

•	$\mathit{\zeta }=0$	$\mathit{\zeta }=1$	$\mathit{\zeta }=2$	$\mathit{\zeta }=3$	$\mathit{\zeta }=4$	$\mathit{\zeta }=5$
$s=0$	0	41.1590	62.1136	77.7982	90.8557	102.2742
$s=1$	0	−0.0009	−0.0014	−0.0018	−0.0021	−0.0024
$s=2$	0	−30.3708	−46.5563	−58.4453	−68.3112	−76.9282
$s=3$	0	−47.9540	−71.9309	−90.9137	−106.3993	−119.8867
$s=4$	0	−38.3632	−57.5448	−71.9309	−84.9194	−95.9094
$s=5$	0	−25.5754	−38.3632	−47.9540	−55.9463	−63.9396

and Figure 1.

Example 4.

Consider the problem

$$\left\{\begin{array}{c}\left({\nabla }_{-1}^{1.5}w\right)\left(\zeta \right)+\mathfrak{f}\left(\zeta ,w(\zeta \right))=0,\zeta \in {\mathbb{N}}_2^5,\hfill \\ w\left(0\right)=0,w\left(5\right)=w\left(1\right)+w\left(2\right).\hfill \end{array}\right.$$

(20)

Here $k=0$, $l=5$, $d=2$, $\eta =1.5$, $\mu ={\displaystyle \frac{1}{3}}$, and

$$\mathfrak{f}(\zeta ,r)=C{e}^{-{\zeta }^2}r\left|{tan}^{-1}\left({\zeta }^2{(r+1)}^3\right)\right|+e^{{\zeta }^2}\sqrt{\left|r+1\right|},$$

with $C>0$. Clearly,

$$m\left(\zeta \right)=\underset{\left|r\right|\to \infty }{lim}{\displaystyle \frac{\mathfrak{f}\left(\zeta ,r\right)}{r}}={\displaystyle \frac{C\pi }{2}}{e}^{-{\zeta }^2},\zeta \in {\mathbb{N}}_0^5.$$

Now, we calculate $g\left({\zeta }^{*}\right)$. The Green’s function associated with (20) is

$$\mathcal{G}(\zeta ,s)=\left\{\begin{array}{c}{\mathcal{G}}_1(\zeta ,s),s\le min\{t,2\},\hfill \\ {\mathcal{G}}_2(\zeta ,s),\zeta +1\le s\le 2,\hfill \\ {\mathcal{G}}_3(\zeta ,s),3\le s\le \zeta ,\hfill \\ {\mathcal{G}}_4(\zeta ,s),s\ge max\{\zeta +1,3\},\hfill \end{array}\right.$$

with

$${\mathcal{G}}_1(\zeta ,s)={\displaystyle \frac{{\mathfrak{H}}_{0.5}(\zeta ,0){\mathfrak{H}}_{0.5}(5,s-1)}{1.6276}}-{\displaystyle \frac{{\mathfrak{H}}_{0.5}(\zeta ,0){\mathfrak{H}}_{1.5}(2,s-1)}{4.8828}}-{\mathfrak{H}}_{0.5}(\zeta ,s-1),$$

$${\mathcal{G}}_2(\zeta ,s)={\displaystyle \frac{{\mathfrak{H}}_{0.5}(\zeta ,0){\mathfrak{H}}_{0.5}(5,s-1)}{1.6276}}-{\displaystyle \frac{{\mathfrak{H}}_{0.5}(\zeta ,0){\mathfrak{H}}_{1.5}(2,s-1)}{4.8828}}$$

$${\mathcal{G}}_3(\zeta ,s)={\displaystyle \frac{{\mathfrak{H}}_{0.5}(\zeta ,0){\mathfrak{H}}_{0.5}(5,s-1)}{1.6276}}-{\mathfrak{H}}_{0.5}(\zeta ,s-1)$$

and

$${\mathcal{G}}_4(\zeta ,s)={\displaystyle \frac{{\mathfrak{H}}_{0.5}(\zeta ,0){\mathfrak{H}}_{0.5}(5,s-1)}{1.6276}}.$$

Then,

$$\gamma ={\displaystyle \frac{{\mathfrak{H}}_{1.5}(5,1)-\frac{1}{3}\left({\mathfrak{H}}_{2.5}(2,0)-{\mathfrak{H}}_{1.5}(2,0)\right)}{1.6276}}=3.8272,$$

$$g\left(\zeta \right)={\displaystyle \frac{\left(5.7408-t+1\right)\mathrm{\Gamma }\left(\zeta +0.5\right)}{\mathrm{\Gamma }\left(1.5\right)\mathrm{\Gamma }\left(\zeta \right)}},\zeta \in {\mathbb{N}}_0^5,$$

$${\zeta }^{*}=\lfloor 2.9136\rfloor =2,$$

and

$$g\left({\zeta }^{*}\right)={\displaystyle \frac{\left(4.7408\right)\mathrm{\Gamma }\left(2.5\right)}{\mathrm{\Gamma }\left(1.5\right)\mathrm{\Gamma }\left(2\right)}}=7.1112.$$

Since

$${\displaystyle \frac{1}{g\left({\zeta }^{*}\right)}}=0.1406,$$

by Theorem 6, we can ensure that (20) has a nontrivial solution defined on ${\mathbb{N}}_0^5$ for all

$$0<C<{\displaystyle \frac{2}{g\left({\zeta }^{*}\right)\pi }}\approx 0.0895.$$

Note that in this case μ is satisfying (14) and as one can see from the values of $\mathcal{G}(\zeta ,s)$ presented in

Table 4. Values of $\mathcal{G}(\zeta ,s)$.

•	$\mathit{\zeta }=0$	$\mathit{\zeta }=1$	$\mathit{\zeta }=2$	$\mathit{\zeta }=3$	$\mathit{\zeta }=4$	$\mathit{\zeta }=5$
$s=2$	0	1	0.7088	0.6360	0.6170	0.6160
$s=3$	0	1.1520	1.7280	1.1600	1.0200	0.9600
$s=4$	0	0.9216	1.3824	1.7280	1.0160	0.7680
$s=5$	0	0.6144	0.9216	1.1520	1.3440	0.5120

and Figure 2, we have that the Green’s function is positive. As a consequence, by Theorem 6, if $r>0$, then problem (20) has a positive solution.

7. Conclusions

In this manuscript, we studied a class of nabla fractional difference problems with multi-point boundary conditions depending on a real parameter. We obtained the exact expression of the related Green’s function and we deduced some very important properties of it. In detail, we obtained an upper bound of the sum of it, and then we established some existence results based on this bound and using the Leray–Shauder alternative. Then, we were able to obtain some bounds of the parameter in which the Green’s function is strictly positive and we showed the existence of strictly positive solutions of the considered problem, which we consider to be the main novelty of this work. This has never been done in the literature for such kinds of problems, and this new idea can be very helpful for other researchers in their attempts to deduce the existence of positive solutions of fractional problems with parameter dependence. Moreover, it can be extended in order to obtain nonexistence or multiplicity results. Another possible future approach would be applying this method to singular fractional-order systems with faults, since they are likely to occur in real fractional-order systems, or to fractional difference multi-agent systems, since these systems are very common.