Anomalous Drug Transport in Biological Tissues: A Caputo Fractional Approach with Non-Classical Boundary Modeling

Abstract

This paper focuses on the numerical modeling of drug diffusion in biological tissues using fractional time-dependent parabolic equations with non-local boundary conditions. The model includes a Caputo fractional derivative to capture the non-local effects and memory inherent in biological processes, such as drug absorption and transport. The theoretical framework of the problem is based on the work of Alhazzani, et al.,which demonstrates the solution’s goodness, existence, and uniqueness. Building on this foundation, we present a robust numerical method designed to deal with the complexity of fractional derivatives and non-local interactions at the boundaries of biological tissues. Numerical simulations reveal how fractal order and non-local boundary conditions affect the drug concentration distribution over time, providing valuable insights into drug delivery dynamics in biological systems. The results underscore the potential of fractal models to accurately represent diffusion processes in heterogeneous and complex biological environments.

1. Introduction

In recent decades, the study of initial boundary value problems (IBVPs) with non-local boundary conditions has become one of the mainstays of applied mathematics. This growing interest has been driven by the wide practical applications of these problems in various fields, such as physics, engineering, biological sciences, and even economics and environmental sciences. The importance of these problems lies in their ability to describe complex phenomena with non-classical behaviors, such as memory effects, anomalous diffusion, and non-local spatial interactions that extend beyond the limits of traditional description using classical differential equations (Kilbas et al. [1]; Podlubny [2]). Non-local boundary conditions represent a new paradigm that takes into account the global effects of the entire system, rather than being limited to local properties at the boundaries. For example, in physics, these models are used to study diffusive heat systems that depend on the properties of materials distributed throughout the structure, while in biology, they contribute to the characterization of the diffusion of chemicals or drugs through biological tissues that exhibit inhomogeneous microscopic variations. In parallel, fractional differential equations have become a powerful mathematical tool that allows accurate modeling of systems with non-local spatiotemporal properties. By incorporating fractional derivatives, these equations provide an effective framework for representing phenomena that depend on the time history of the system and the effects of extended spatial interactions (Mainardi [3]; Magin [4]). For example, these models can be used to understand non-Newtonian fluid dynamics, analyze the spread of diseases, or even study smart materials in engineering.

Classical integer differential equations are a powerful and effective tool for describing local interactions in physical and biological systems. However, these equations show clear limitations when dealing with processes that depend on historical effects or past states, as well as those involving non-local spatial interactions. Fractional-order equations, which rely on non-integer derivatives, such as the Caputo derivative and the Riemann–Liouville derivative, have emerged as advanced mathematical tools capable of addressing these limitations (Gafiychuk et al. [5]; Ladaci et al. [6]). The advantage of these equations is their ability to incorporate memory effects, anomalous diffusion, and long-range interactions into mathematical models. This makes them suitable for describing complex phenomena that cannot be accurately expressed using classical models. For example, fractional differential equations are used to understand heat transfer dynamics, analyze viscoelastic materials, and model diffusion in heterogeneous media, expanding their applications in physics, engineering, and biological sciences (Mainardi [3]; Fang and Wang [7]). Moreover, these models offer greater flexibility in characterizing the dynamic behaviors of systems, such as hysteresis and time-dependent interactions, which are critical in studying biological processes like drug diffusion within tissues or complex environmental systems where non-local effects play a significant role.

Fractional differential equations are an essential mathematical tool for modeling complex processes in many fields, and one prominent application is modeling drug diffusion in biological tissues. In such systems, drug transport depends on the dynamic interplay between local tissue properties and long-range spatial interactions, including boundary effects. Fractional derivatives provide a natural framework for capturing the memory effects inherent in tissues, while non-local boundary conditions, often formulated as integral conditions, capture the global influence of the surroundings on drug distribution within the tissue. In recent years, studies have made significant progress in the mathematical and numerical understanding of fractional equivalent equations with non-local boundary conditions. These equations generalize classical equivalent models by incorporating fractional time derivatives, such as the Caputo or Caputo–Fabrizio derivative, to characterize time-dependent diffusion processes (Phong and Long [8]; Bashir et al. [9]). Similarly, non-local boundary conditions extend the applicability of these models by allowing the boundary condition to depend on integrated averages of system values, rather than being limited to local properties at the boundary (Mesloub and Gadain [10]; Liu et al. [11]).

In a related context, fixed point theory plays a crucial role in the analysis of complex fractal models, offering powerful mathematical tools to guarantee the existence, uniqueness, and stability of solutions. Recent studies, such as those by Balegh and Ghezal [12] and El Mamouni et al. [13], underscored the effectiveness of these theories in modeling dynamical systems involving time delays and non-local effects, particularly in applications such as epidemic modeling and tumor dynamics. For instance, Ghezal and Attia [14] employed stochastic fractal equations to simulate tumor growth and the diffusion of chemicals in biological tissues, thereby enhancing the understanding of complex interactions between fractal structures and heterogeneous biological environments. Furthermore, studies like that by El Hassani et al. [15] have demonstrated the relevance of saturated fractal derivatives—such as the fractal– fractal Hataf derivative—in modeling the abnormal spread of viruses like SARS-CoV-2, highlighting the stability of solutions through the use of Lipanov theory. These developments underscore the significant potential of fractal-based models in improving the accuracy of biological system simulations and reinforce the necessity of a robust numerical framework for incorporating these concepts into drug diffusion models, as addressed in this study.

Theoretically, research has focused on studying the properties of these models, including proving the existence, uniqueness, and stability of solutions. Advanced techniques such as energy inequality and functional analysis have been used to understand the regularity and stability of solutions (Cannon [16]; Alhazzani et al. [17]). On the other hand, numerical studies have addressed the challenges posed by fractional derivatives, which are characterized by their singular nature, and non-local interactions. Numerical methods such as the fractional finite difference method and spectroscopy have proven effective in providing accurate approximations of these models, enabling the simulation of complex systems (Xianjuan and Chuanju [18]; Jian et al. [19]; Amattouchi et al. [20]).

In the context of biological applications, these models are of particular importance in understanding the dynamics of drug delivery systems. Drug absorption and distribution within biological tissues depend on both the tissue microstructure and interactions at the boundaries, making non-local conditions essential for accurately characterizing these systems. For example, by formulating drug diffusion as a two-dimensional fractional equivalent equation with non-local boundary conditions, the complex relationship between the memory effects within tissues and the spatially distributed diffusion at the boundaries can be captured. This framework enhances the accuracy of drug delivery modeling, opening new avenues for improving diffusion-based medical therapies and dose control.

Building on the seminal work of Alhazzani et al. [17], this study focuses on the analysis of the two-dimensional fractional parabolic Caputo partial differential equation integrated with the Bessel factor, which is defined within a certain rectangular range $\mathsf{\Psi }=\left]0,\alpha \right[\times \left]0,\beta \right[\subset {\mathbb{R}}^2$. The main goal is to study the problem of finding a function $N:\left]0,\alpha \right[\times \left]0,\beta \right[\times \left[0,T\right]⟶\mathbb{R}$ that satisfies the fractional Caputo partial differential equation

$$L\left(N\right)={\partial }_t^{\tau }N-{\left(xy\right)}^{-1}div(xy\nabla N)+N=K_0(x,y,t),$$

(1)

where $\tau \in \left]0,1\right]$ denotes the fractional order and ${\partial }_t^{\tau }$ is the Caputo fractional derivative, defined by

$${\partial }_t^{\tau }U(x,t)={\mathsf{\Gamma }}^{-1}(1-\tau ){\displaystyle \underset{0}{\overset{t}{\int }}}{U}_{\gamma }(x,\gamma ){(t-\gamma )}^{-\tau }d\gamma ,$$

with $\mathsf{\Gamma }(.)$ representing the Gamma function. The model is supplemented by the initial condition

$$N(x,y,0)=f(x,y),$$

(2)

as well as the Neumann boundary conditions

$$N_x(\alpha ,y,t)=N_y(x,\beta ,t)=0,$$

(3)

and the non-local weighted boundary integral conditions

$${\displaystyle \underset{0}{\overset{\alpha }{\int }}}xN(x,y,t)dx={\displaystyle \underset{0}{\overset{\beta }{\int }}}yN(x,y,t)dy=0.$$

(4)

Additionally, the compatibility conditions require

$$\begin{array}{cc}\hfill f_x(\alpha ,y)& =f_y(x,\beta )=0,\hfill \\ \hfill {\displaystyle \underset{0}{\overset{\alpha }{\int }}}xf(x,y)dx& ={\displaystyle \underset{0}{\overset{\beta }{\int }}}yf(x,y)dy=0.\hfill \end{array}$$

Here, $K_0(x,y,t)$ belongs to the Hilbert space ${\mathbb{L}}_2(0,T;{\mathbb{L}}_{2,xy}(\left]0,\alpha \right[\times \left]0,\beta \right[))$ defined with the weight $xy$, and $f(x,y)$ belongs to the weighted Sobolev space $V_{2,\lambda }^1(\left]0,\alpha \right[\times \left]0,\beta \right[)$. These conditions collectively ensure a well-posed formulation that captures the complexities of fractional diffusion processes with non-local interactions. The appearance of the weight factor ${\left(xy\right)}^{-1}$ in the diffusion operator of Equation (1) is not arbitrary; it stems from the modeling of diffusion phenomena in geometrically heterogeneous media. This Bessel-type factor naturally arises when deriving diffusion equations in cylindrical or polar coordinates, where the radial symmetry of the physical context introduces scaling terms inversely proportional to the spatial variables, as seen in classical models of heat or mass transfer. In the context of fractional diffusion, such a weight modifies the operator’s spectral properties and reflects the influence of microstructural heterogeneities or anisotropic transport in biological tissues, particularly in porous or vascularized environments. This approach aligns with the mathematical treatment of weighted fractional diffusion equations used to model anomalous transport processes, where the weights capture the essential geometric or material characteristics of the medium. Therefore, the inclusion of ${\left(xy\right)}^{-1}$ serves to enhance the physical relevance of the model by accounting for local scaling effects in two-dimensional biological domains, especially in applications such as targeted drug delivery within structured tissues.

The main objective of this study is to develop a robust and efficient numerical framework for solving two-dimensional fractional parabolic equations with non-local boundary conditions, especially in the context of modeling drug diffusion in biological tissues. In this study, we present a new framework that addresses the challenges of time-fractional derivatives, which depend on the complete history of the system’s temporal behavior, and integrated boundary conditions that reflect the non-local interactions between the system and its environment. By incorporating these elements, numerical stability and high accuracy can be ensured in various simulations and applications. The main challenge is to incorporate non-local spatial and historical effects into mathematical models, which classical models cannot adequately handle. By addressing these issues, the proposed framework aims to improve our understanding of how the fractal order affects the spatiotemporal distribution of drug concentrations within tissues, including non-local effects that occur at the boundaries or in specific regions of the system. The practical significance of this study is to improve the modeling of drug delivery in biological tissues, where both tissue-level interactions and boundary effects are essential to understanding biological diffusion mechanisms. Fractional effects reflect the unusual slowness of diffusion, while non-local boundary conditions capture interactions between tissues and other parts of the body, which greatly influence treatment outcomes. Thus, improving models in this area has important implications for the development of medical treatments in general. By developing this numerical framework, this study aims to provide a powerful tool to support future studies in the fields of biology and biomedical engineering while opening new avenues for research into non-local temporal and spatial effects on drug diffusion.

Motivated by the increasing demand for accurate models of drug diffusion in heterogeneous biological tissues, this study proposes a novel mathematical and numerical framework that couples time-fractional diffusion dynamics with non-local boundary conditions. While previous works have either focused on fractional diffusion with classical boundaries or addressed non-local effects without memory considerations, our approach unifies both features within a single model governed by a Caputo fractional derivative and a weighted Bessel-type diffusion operator. This formulation allows capturing memory-dependent transport phenomena and spatial heterogeneity effects that are typically overlooked in conventional models. The main novelty of our paper lies in the integrated treatment of fractional dynamics and boundary-driven interactions using a dedicated numerical scheme that ensures both stability and accuracy when handling the singularity of memory kernels and the complexity of non-local boundary terms. Unlike existing methods that rely on asymptotic or simplified conditions, our approach provides a versatile tool capable of analyzing realistic diffusion scenarios, with direct applications to biomedical engineering and drug delivery systems. Theoretical analysis and extensive simulations demonstrate how the combined effect of the fractional order, boundary configuration, and spatial weighting significantly influences drug distribution patterns, offering new perspectives on model fidelity and practical relevance.

This paper begins with an introduction that provides a comprehensive background on fractional differential equations and their importance in modeling drug diffusion in biological tissues. The Theoretical Framework and Key Results section explains the mathematical basis and analytical results, including the existence, uniqueness, and stability of the solutions. The numerical simulation section presents the methodology and numerical simulations, supported by detailed visualizations and analyses of diffusion patterns under different conditions. Finally, the Conclusions section summarizes the results, highlighting the contributions of the study and their implications for future research in fractal modeling and biomedical engineering.

2. Theoretical Framework and Key Results

The foundational work by Alhazzani et al. [17] provided a rigorous mathematical analysis of the solvability of a single fractional time-parabolic equation with non-classical boundary conditions, proving the existence and uniqueness of solutions and introducing stability bounds that ensure small changes in the initial or boundary conditions do not lead to large deviations in the solutions. The researchers relied on modern techniques of functional analysis and energy inequality, providing a powerful theoretical framework for studying fractional derivatives and non-local boundary conditions. These results highlight the advanced mathematical understanding of fractional partial differential equations, which combine temporal memory effects with non-local spatial interactions, making them suitable for describing complex physical and biological systems.

• Key Theoretical Results

• A Priori Estimate
  Theorem 1 establishes an upper bound for the solution N in terms of its dependence on the initial data f and the source term $K_0$:

  $${∥N∥}_{{\mathbb{L}}_2(0,T,V_{2,xy}^{1,\delta }(\left]0,\alpha \right[\times \left]0,\beta \right[))}^2\le D_0(\kappa +1)({∥K_0∥}_{{\mathbb{L}}_2(0,T,{\mathbb{L}}_{2,xy}(\left]0,\alpha \right[\times \left]0,\beta \right[))}^2+{∥f∥}_{V_{2,xy}^1(\left]0,\alpha \right[\times \left]0,\beta \right[)}^2),$$

  where $D_0$ and $\kappa$ are positive constants given by

  $$D_0=max\left\{d_0,{(1-\tau )}^{-1}{\mathsf{\Gamma }}^{-1}(1-\tau )T^{1-\tau }max\left\{1,1+{\left(\alpha \beta /2\right)}^3/2\right\}\right\},$$

  and $\kappa ={\tau }^{-1}{D}_0{T}^{\tau }\mathsf{\Gamma }\left(\tau \right){\mathsf{\Phi }}_{\tau ,\tau }\left(D_0{T}^{\tau }\right)max\left\{1,T\right\},$ where $2d_0=max\{3.2{\alpha }^2+2{\beta }^2+2(\alpha$ ${\beta /2)}^2\}$. Here, ${\mathsf{\Phi }}_{\tau ,{\tau }^{\prime }}\left(x\right)$ denotes the Mittag–Leffler function, where ${\mathsf{\Phi }}_{\tau ,{\tau }^{\prime }}\left(x\right)={\displaystyle \sum _{j\ge 0}}{x}^j/\mathsf{\Gamma }(\tau j+{\tau }^{\prime })$. These constants are independent of N, ensuring that the bound holds for a wide range of inputs and providing stability to the problem formulation.
  Sketch of Proof of Theorem 1
  The proof of Theorem 1 follows a standard energy estimate approach adapted to the fractional framework.
  We begin by taking the inner product of the governing equation with a suitable test function that includes both the solution and its fractional derivatives.
  By carefully computing the inner products term by term, especially those involving the fractional derivative and the non-local integral operators, we obtain a differential inequality involving ${\parallel N\parallel }_{V_{2,\lambda }^1\left(\mathsf{\Omega }\right)}$, $\parallel N_x{\parallel }_{L_{\lambda }^2\left(\mathsf{\Omega }\right)}$, and $\parallel N_y{\parallel }_{L_{\lambda }^2\left(\mathsf{\Omega }\right)}$.
  Using Young’s inequality, the fractional Poincaré-type inequalities, and properties of the Mittag–Leffler function, we derive an inequality that bounds the $L^2$ norms of N in terms of the source term $K_0$ and the initial data f.
  Finally, by applying fractional integration and Grönwall-type estimates for fractional derivatives, we conclude with the desired a priori estimate.
• Operator Properties
  Proposition 1 proves that the operator $P:B⟶Y,$ where Y and B are Banach spaces, is closable, a fundamental property for the well-posed extension of P. Additionally, Theorem 2 guarantees that the problem in Equations (1)–(4) has a unique solution, namely $N=P^{-1}(K_0,f)=\overline{P^{-1}}(K_0,f)$, which depends continuously on the inputs $K_0\in {\mathbb{L}}_2(0,T,{\mathbb{L}}_{2,xy}(\left]0,\alpha \right[\times \left]0,\beta \right[))$ and $f\in V_{2,xy}^1(\left]0,\alpha \right[\times \left]0,\beta \right[)$. This result demonstrates the robustness of the solution under the given conditions.
  Sketch of Proof of Proposition 1
  The proof of Proposition 1 follows standard operator theory arguments within the framework of Banach spaces.
  We begin by establishing an a priori estimate of the form

  $${\parallel N\parallel }_B\le D_0(\kappa +1){\parallel PN\parallel }_Y,\forall N\in D\left(P\right),$$

  where $D_0$ and $\kappa$ are constants independent of N.
  This inequality implies that the graph of P is closed in $B\times Y$, which is equivalent to the operator P being closable.
  Moreover, by taking the closure $\overline{P}$ and observing that $R\left(P\right)$ is dense in Y, we deduce that $R\left(\overline{P}\right)=R\left(P\right)=Y$, confirming the surjectivity of the closed operator.
  This guarantees that $P^{-1}$ exists on Y and is bounded, thereby ensuring that the solution depends continuously on the data.
  The proof strategy mirrors classical approaches as detailed in the work of Mesloub [21], relying on operator closure properties and norm estimates.
• Uniqueness and Surjectivity of  $\mathit{P}$
  Theorem 3 provides the surjectivity condition for the operator P by showing that if $\pi \in {\mathbb{L}}_{2,xy}(\left]0,\alpha \right[\times \left]0,\beta \right[\times \left[0,T\right])$ satisfies ${(L\mathsf{\Omega },\pi )}_{{\mathbb{L}}_{2,xy}(\left]0,\alpha \right[\times \left]0,\beta \right[\times \left[0,T\right])}=0$ for all $\mathsf{\Omega }(x,y,t)\in D\left(P\right)$ with homogeneous initial conditions $\mathsf{\Omega }(x,y,0)=0$, then $\pi =0$ almost everywhere in $\left]0,\alpha \right[\times \left]0,\beta \right[\times \left[0,T\right],$ where $\overline{P}$ denotes the closure of P and $D(\overline{P})$ is its domain of definition. This result is critical in proving $R(\overline{P})=Y$, completing the argument for the existence of a unique solution.
  Sketch of Proof of Theorem 3
  The proof of Theorem 3 relies on the classical duality argument in Hilbert space settings combined with energy estimates adapted to the fractional-order operators.
  We consider the adjoint formulation. Assume that $\pi \in {\mathbb{L}}_{2,xy}\left((0,\alpha )\times (0,\beta )\times (0,T)\right)$ satisfies

  $${(L\mathsf{\Omega },\pi )}_{{\mathbb{L}}_{2,xy}}=0,$$

  for all $\mathsf{\Omega }\in D\left(P\right)$ with the homogeneous initial condition $\mathsf{\Omega }(x,y,0)=0$.
  By introducing appropriate test functions constructed via fractional integration of $\pi$ and carefully applying integration by parts adapted to the Caputo derivative and the divergence terms, we derive an energy identity involving ${\parallel \mathsf{\Omega }\parallel }^2$, ${\parallel \nabla \mathsf{\Omega }\parallel }^2$, and fractional norms of $\pi$.
  Through the use of Poincaré-type inequalities, Young’s inequality, and the properties of fractional integral operators (in particular, the positivity and coercivity of certain fractional norms), we deduce that $\pi =0$ almost everywhere in the domain.
  This implies that the range of the closure $\overline{P}$ is the entire space Y, establishing the surjectivity.
  The detailed proof involves estimating the energy functional derived from the weak formulation, handling boundary terms via the imposed conditions, and utilizing density arguments similar to those in Lions’ framework for evolution equations.

The results presented by Alhazzani et al. [17] establish a solid theoretical foundation for fractional parabolic equations with non-classical boundary conditions. The a priori estimates, operator properties, and surjectivity conditions ensure the existence, uniqueness, and stability of solutions, providing essential tools for further analytical and numerical explorations in modeling complex diffusion phenomena. Building upon this solid theoretical groundwork, our study seeks to advance the field by introducing several distinctive contributions that extend beyond the scope of Alhazzani et al. [17]. Specifically, we focus on the application of the Caputo fractional derivative in conjunction with non-local boundary conditions to model anomalous drug transport phenomena in biological tissues, a context not explored by Alhazzani et al. [17]. Our work emphasizes the dynamic interplay between memory effects and boundary-driven interactions, which we investigate systematically through detailed numerical simulations. These simulations illustrate, for the first time, how variations in fractional order, boundary conditions, source location, and computational resolution directly influence the spatiotemporal diffusion patterns. Moreover, unlike the theoretical scope of Alhazzani et al., which was confined to existence and uniqueness results, our study extends the analysis to practical modeling scenarios relevant to biomedical applications. We thus provide a comprehensive numerical assessment that highlights the impact of model parameters on diffusion behavior, thereby offering novel insights and validating the theoretical framework in a real-world modeling context.

In addition to establishing the theoretical and numerical contributions, it is important to clarify the practical relevance of our modeling framework within biomedical applications. The use of fractional-order derivatives—particularly in the Caputo sense—has been increasingly recognized as a powerful tool for describing transport processes in heterogeneous biological tissues, where classical diffusion models fail to capture the observed anomalous behaviors. As demonstrated by Metzler and Klafter [22], fractional dynamics naturally arise from random walk models with memory effects, which are directly linked to the irregular microstructure and trapping mechanisms inherent in biological environments. In this context, the fractional order serves as a phenomenological parameter that characterizes deviations from classical Fickian diffusion, thus reflecting measurable tissue properties such as the porosity, tortuosity, and retention time of the drug molecules. Moreover, Magin [4] emphasized the utility of fractional calculus in bioengineering, showing its effectiveness in modeling hereditary phenomena and complex time-dependent behaviors observed in biological systems, including drug transport and membrane dynamics. The fractional order can, therefore, be interpreted as a macroscopic indicator of the medium’s structural heterogeneity and viscoelastic response, parameters which can be experimentally inferred from tracer studies or transport measurements. By integrating these insights, our model not only advances the theoretical analysis but also lays the groundwork for calibrating fractional parameters against biological data, thereby enhancing its applicability to experimental drug delivery systems. This connection underscores the potential of fractional models as both predictive and interpretive tools in biomedical research, particularly in contexts requiring accurate descriptions of anomalous transport phenomena.

3. Numerical Simulation of Fractional Drug Diffusion Models

Numerical simulations play a crucial role in understanding the complex dynamics of drug diffusion in biological tissues, especially when modeled using fractional partial differential equations that consider temporal memory effects and non-local interactions. These simulations are a powerful tool for providing accurate visual and quantitative insights into the spatial and temporal distribution of drug concentration, enabling analysis of the influence of various parameters such as the order of fractional derivatives and non-traditional boundary conditions. Compared with purely theoretical analysis, simulations demonstrate the ability to capture complex phenomena such as anomalous diffusion, where diffusion is slower or faster than the natural model, as well as memory effects that reflect the system’s dependence on its history. This section features a review of various aspects of numerical modeling, including computational network design and fractional differential techniques, with the results presented through sophisticated visualizations that clearly illustrate the different dynamic patterns. Furthermore, a comprehensive interpretation is provided for each result, highlighting the relationship between model settings and biological parameters, enhancing our understanding of system dynamics, and providing a tool for predicting drug distribution behavior in complex biological environments. To effectively capture the complex dynamics of fractional drug diffusion with memory effects and non-local boundary interactions, we adopt a structured numerical methodology that ensures coherence between the mathematical formulation and its computational implementation. The adopted scheme consists of three main stages:

• Spatial Discretization: The spatial domain $\mathsf{\Psi }$ is discretized using a uniform rectangular grid. The Laplacian operator, with Bessel-type weighting reflecting geometric singularities, is approximated by a second-order central difference scheme.
• Temporal Discretization and Memory Effect Handling: The Caputo time-fractional derivative is discretized using a Grünwald–Letnikov approximation, capturing memory-dependent behavior via a weighted sum of the historical time levels. Time integration is handled by an explicit forward Euler method, chosen for its computational simplicity and ability to capture key dynamical features under controlled time steps.
• Treatment of Non-Local Boundary Conditions: The non-local integral boundary conditions are discretized using suitable numerical quadrature formulas and consistently integrated into the time-stepping algorithm, ensuring dynamic coupling between boundary effects and internal diffusion.

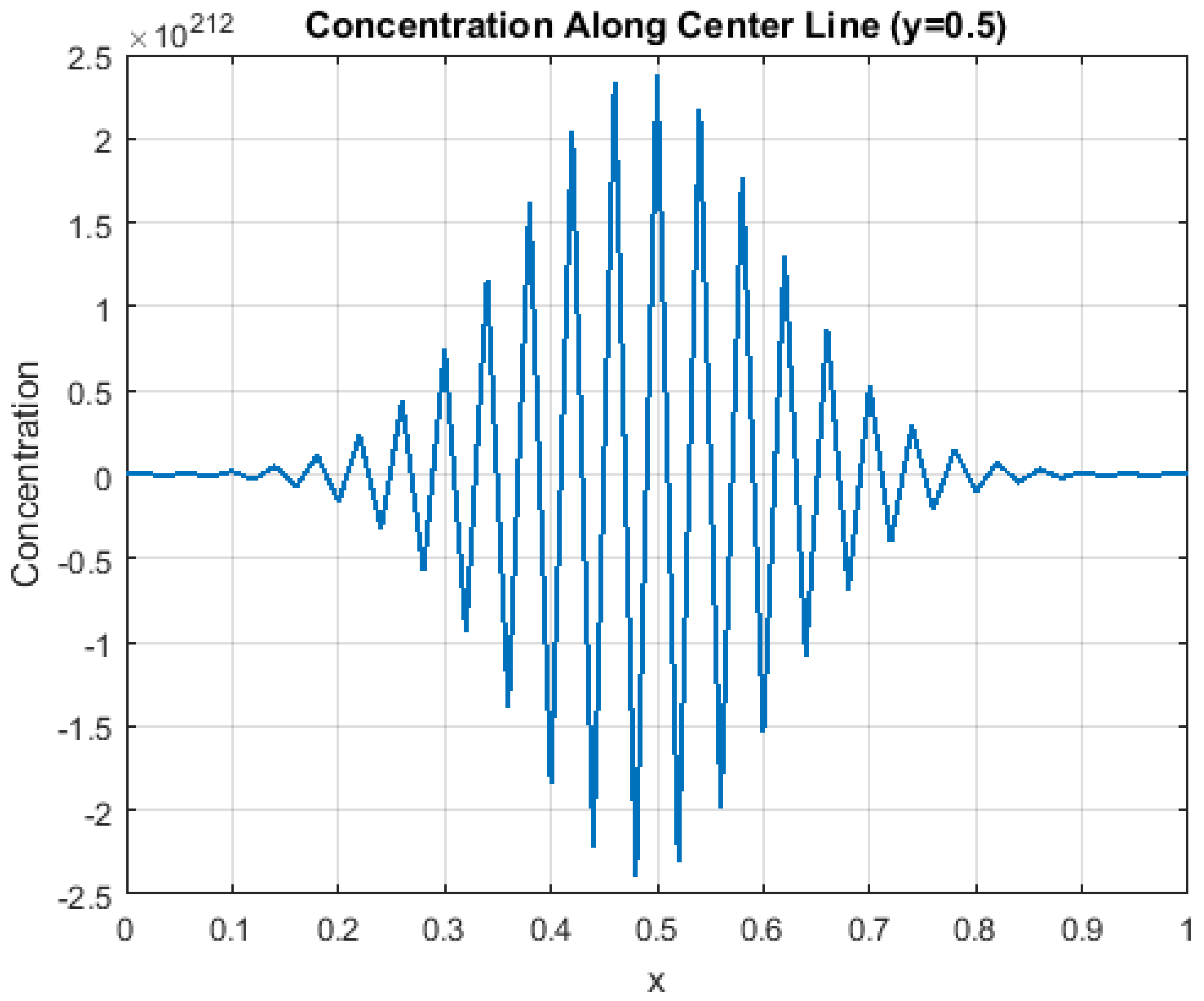
This numerical strategy balances computational efficiency and accuracy while faithfully preserving the intrinsic memory and boundary-driven dynamics of the fractional diffusion process. Validation through grid refinement and convergence analyses confirms the robustness of the proposed scheme. The next sections present simulation results supported by detailed visualizations and interpretations. To illustrate the capabilities of the proposed scheme, we begin by analyzing the concentration profiles along the domain’s centerline, as shown in Figure 1.

This figure (Figure 1) shows the temporal variations in drug concentration along the horizontal centerline (y = 0.5) of the simulated domain, highlighting how the drug diffuses from the initial source and gradually spreads outward. The gradual flattening of the concentration curve over time shows the effect of fractional diffusion dynamics, where fractional time derivatives lead to nonlinear slowing or acceleration of the diffusion process compared with conventional patterns. This visualization simplifies the 2D dynamics to a single cross-sectional view, facilitating the study of the fundamental properties of spatial diffusion and understanding its evolution along a critical axis of the system. In addition, this graphic reflects the balance between local processes and long temporal memory that controls drug diffusion, making it an important analytical tool. This basic analysis provides a basis for extending the study to more complex visualizations that include 3D distribution patterns and the influence of non-local boundary conditions, which helps give a more comprehensive understanding of drug diffusion dynamics in biological tissues.

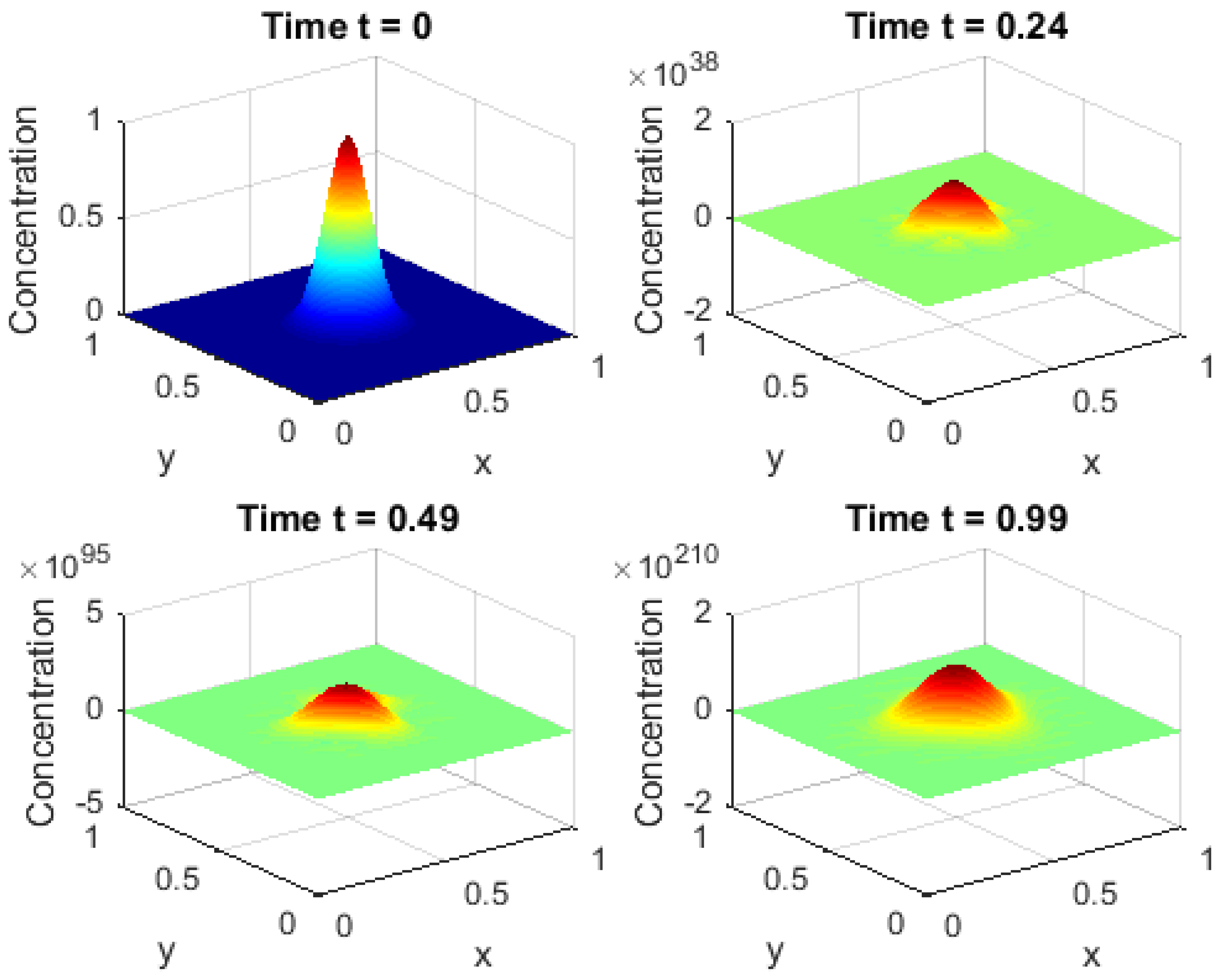
Figure 2 shows a series of snapshots showing the drug concentration distribution at specific time intervals, providing a dynamic visualization of the progression of the diffusion process from an initial state toward a more homogeneous state over time. These frames clearly show the effect of the fractional order on the diffusion rate, with the dynamics of the fractional derivatives contributing to a nonlinear behavior that includes anomalous diffusion and the gradual evolution of gradients within the domain. By analyzing these snapshots, it is possible to understand the relationship between local changes and the overall behavior of the system, revealing how local processes (such as concentration around the initial source) interact with global effects (such as the overall distribution across the domain). These frames also allow tracking the evolution of the entire domain over time, highlighting the spatial patterns that emerge at the domain boundaries and their influence on the diffusion dynamics. After focusing on the behavior along the horizontal centerline, these visualizations complete the analysis by providing a comprehensive three-dimensional view of the drug diffusion, helping to link local and global processes. These frames are a vital tool for understanding the combined effects of fractional derivatives and non-local boundary conditions and form the basis for evaluating model performance and developing more efficient numerical solutions in biological and engineering applications.

Figure 3 highlights the crucial influence of boundaries on drug concentration dynamics by plotting the concentration values at the boundaries ($x=0$ and $y=0$) over time. This visualization reveals how non-local boundary conditions, often represented by integral terms, influence the diffusion process within a domain. The curves highlight the dynamic interaction between the internal points of the system and the boundaries, providing insight into the interrelationship between the internal and boundary-driven dynamics. The figure reflects how integral boundary conditions can lead to unconventional behavior, such as delayed or enhanced effects on the internal distribution of the drug concentration, depending on the degree of spatial interaction and temporal memory embedded in the system. Analyzing this effect is crucial to understanding how domain edges contribute to shaping the internal patterns of diffusion, especially in systems characterized by non-local interactions. Furthermore, the figure provides a link between local effects at the boundaries and the overall patterns governing the entire system, bridging the gap between internal and boundary dynamics. This analysis provides a useful tool for improving diffusion models across unconventional domains, and helps design more accurate strategies for controlling drug distribution in biological and engineering applications.

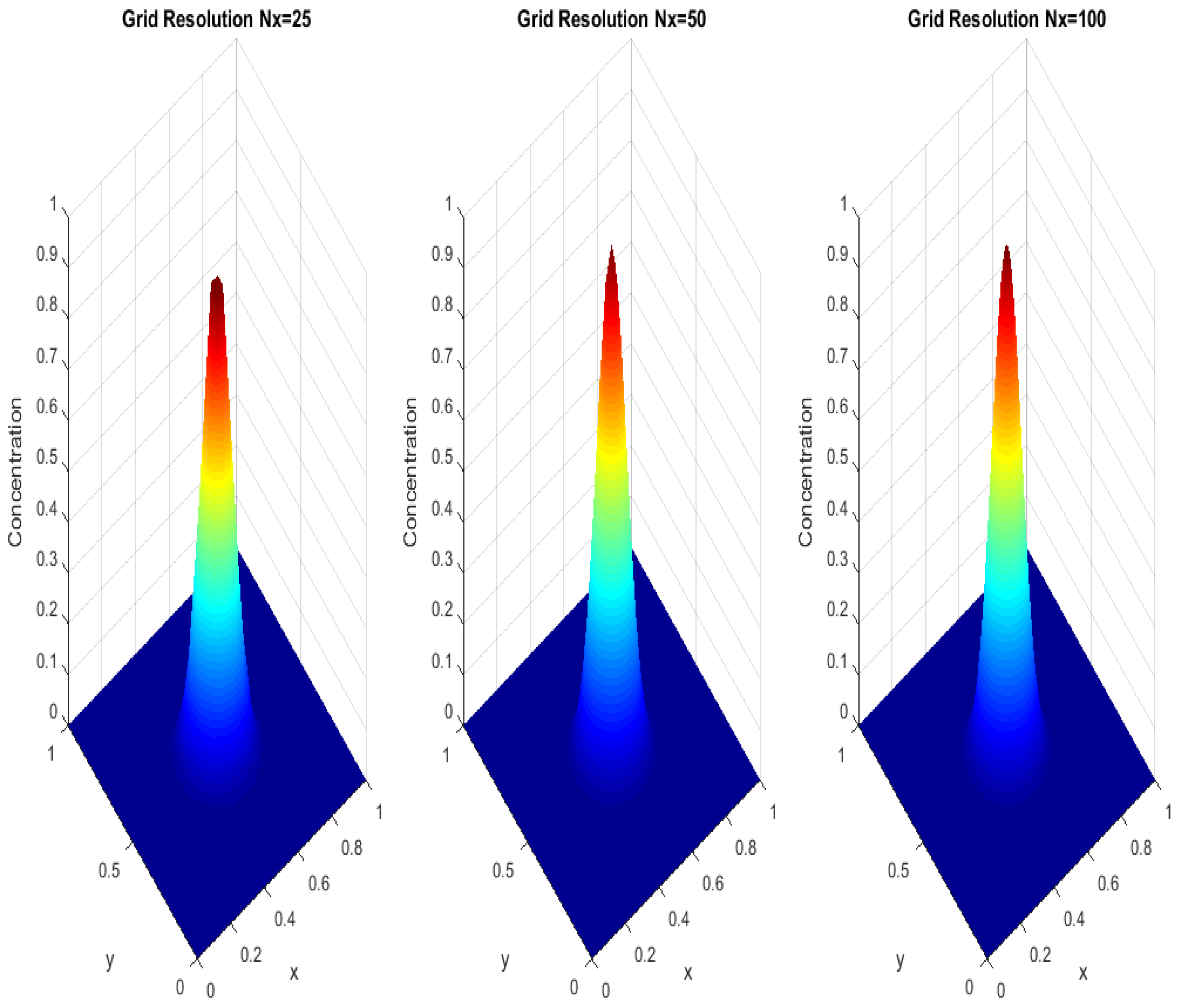
Figure 4 evaluates the impact of numerical grid resolution on the quality and accuracy of the simulation solutions. By comparing the results at different levels of partitioning (e.g., Nx = 25, 50, 100), the figure highlights the delicate balance between computational cost and solution accuracy. Higher-resolution grids show more accurate details of the diffusion process, with better representation of fine gradients and rapid changes in drug concentration, while lower-resolution grids may introduce significant errors, such as over-smoothing or the inability to capture complex system dynamics. The figure illustrates how insufficient numerical partitioning can lead to biases or oversimplifications of the dynamics, highlighting the importance of choosing an appropriate grid resolution that meets the model requirements. Furthermore, this evaluation helps ensure that the simulation results are robust and convergent, as they show low sensitivity to changes in grid resolution at a given level. This analysis contributes to increased confidence in the numerical outputs, making the simulation more reliable and applicable to a wide range of scenarios. It also provides valuable guidance for choosing the optimal mesh resolution, taking into account computational limitations, especially in biological and engineering applications that require accurate modeling of diffusion in complex tissues or materials.

Figure 5 explores the effect of the initial drug source location on diffusion patterns within the domain. By varying the source location $(x_c,y_c)$ across the domain, the figure reveals the sensitivity of the system to initial conditions and how they affect the diffusion process. The distributions resulting from these changes show how the fractional dynamics respond to the source location, with a particular focus on gradient formation and the interaction of the diffusion process with boundaries. This study highlights the flexibility of the model in handling diverse initial configurations, adding depth to the analysis and highlighting the ability to simulate different scenarios involving multi-site drug sources. The results reveal how the source location affects the concentration distribution over time, as interactions with boundaries and internal gradients can significantly alter them. By understanding this relationship between the initial source location and diffusion patterns, this analysis provides a powerful tool in real-world applications, such as targeted drug delivery, where controlling the source location may be necessary to achieve optimal drug distribution in biological tissues. Additionally, this research helps improve targeted delivery strategies and enhance therapeutic efficacy by modeling diffusion behavior in complex environments.

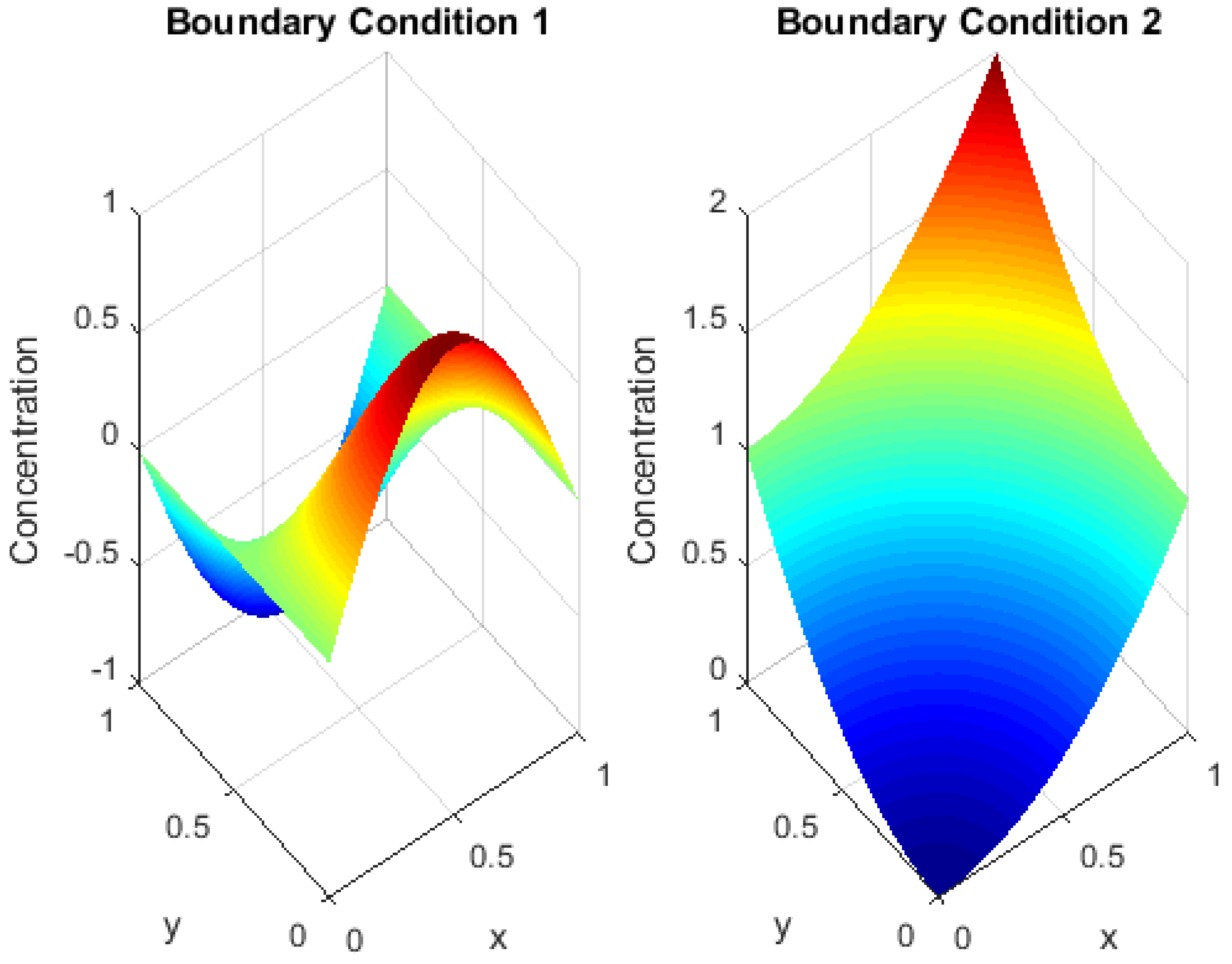
Figure 6 compares the diffusion patterns under different types of boundary conditions, with each subgraph showing the effect of these conditions on the drug concentration distribution, with particular emphasis on the behavior of the system near the edges of the domain. The comparison between conventional and unconventional boundary conditions illustrates how these boundaries shape the concentration distribution over time and how variations in boundary conditions can affect the acceleration or deceleration of diffusion in regions near the boundaries. This comparison underscores the vital importance of boundary conditions in accurately modeling real-world systems, such as drug diffusion in biological tissues or heterogeneous materials, where boundaries can significantly influence system dynamics. By examining the effect of boundary conditions on diffusion behavior, we build on previous insights into the influence of non-local and integrated boundaries, providing a deeper understanding of the role of these boundaries in shaping diffusion patterns along the domain. This analysis contributes to the ability to model complex systems involving non-local interactions and enhances the accuracy of numerical simulations by ensuring a realistic representation of the boundaries that influence diffusion behavior. It also helps guide the development of better strategies for targeted drug delivery or for engineering and biological applications that require accurate modeling of boundary effects.

Figure 7 shows the diffusion velocity at the final time step, calculated as the spatial gradient of the concentration field. The gradient map highlights regions that experience rapid changes in concentration, providing insights into the efficiency and extent of diffusion through the field. This map allows us to identify where diffusion is most effective, as well as regions where the process may be slowed down due to local interactions or boundary effects. The gradient map serves as a quantitative measure of how well a drug diffuses through the field and can be used to assess the exact speed at which a drug diffuses through different regions. These measurements reflect changes in the concentration distribution that occur as a result of complex interactions between non-local boundary conditions and the internal properties of the field. By presenting the diffusion velocity as a final summary, this analysis provides a focused metric that links the findings from the previous figures. It helps comprehensively assess the effectiveness of the model by highlighting how different factors such as the fractional order, boundary conditions, and source location affect the overall diffusion dynamics. This conclusion enhances our understanding of the time efficiency of simulations and contributes to improved strategies for predicting drug transport across tissues in biological and engineering applications.

Remark 1.

In the numerical implementation of the proposed fractional diffusion model, the spatial discretization is performed using a uniform finite-difference grid based on second-order central difference approximations for the Laplacian operator, ensuring consistency with the underlying diffusion dynamics. Time integration is handled via an explicit forward Euler scheme, chosen for its simplicity and ability to capture the main features of the evolving concentration field within the intended simulation horizon. To account for the temporal memory effects inherent in fractional Caputo derivatives, a discrete convolution-based approach is incorporated within the time- stepping framework. Specifically, the contribution of the fractional time derivative is approximated using a Grünwald–Letnikov-type discretization, which involves a weighted summation over all previous time levels, reflecting the non-local memory integral. This methodology effectively captures the history-dependent behavior of the system and enables the accurate simulation of anomalous diffusion processes driven by fractional dynamics. The combination of explicit time-stepping with memory-integrated approximation strikes a balance between computational efficiency and the faithful representation of the fractional-order dynamics. Moreover, the stability and convergence of the scheme are carefully monitored through grid refinement studies and time step sensitivity analyses, ensuring the robustness of the simulation results presented. This strategy allows the model to faithfully reflect both the spatial diffusion mechanisms and the long-range temporal memory effects that characterize the drug transport phenomena in biological tissues.

Remark 2.

To complement the grid sensitivity analysis presented in Figure 4, we conducted a quantitative assessment of the numerical error by evaluating the difference between solutions obtained upon successive grid refinements. Specifically, the $L_2$ norm of the difference between solutions computed with $N_x=100$ and $N_x=50$ was compared against that between $N_x=50$ and $N_x=25$. The observed reduction in the error norm with grid refinement confirms the expected convergence behavior of the finite difference scheme applied to the fractional diffusion model. The decreasing trend of the numerical discrepancy upon mesh refinement serves as a practical indicator of numerical consistency and stability. This comparative approach, widely adopted in numerical analysis, validates that the discretization captures the main diffusion dynamics without introducing significant numerical artifacts. Moreover, the convergence trend supports the reliability of the results presented, ensuring that the key phenomena illustrated in the simulation outputs are not artifacts of discretization but reflect the genuine behavior of the modeled system.

Remark 3.

The numerical simulation of fractional partial differential equations (PDEs) inherently involves a higher computational cost compared with classical integer-order models. This increase is mainly due to the non-local nature of the fractional derivatives, which require the evaluation of historical states at each time step, thereby increasing both the memory usage and computational time. In our implementation, the time-stepping scheme accumulates historical contributions explicitly, which becomes more computationally demanding as the simulation progresses. To manage this trade-off between numerical accuracy and computational efficiency, we carefully selected grid resolutions and time step sizes that ensured numerical stability while maintaining reasonable computational times. The grid sensitivity analysis (Figure 4) confirms that a mesh of $N_x=50$ strikes a good balance, capturing the essential diffusion dynamics without excessive computational cost. Although finer grids and smaller time steps would theoretically yield higher accuracy, they would substantially increase the computation time due to the memory effect intrinsic to fractional models. Therefore, our simulation settings represent a practical compromise, ensuring that the key physical features of anomalous diffusion are accurately captured without imposing prohibitive computational demands.

Remark 4.

In the context of drug diffusion in biological tissues, boundary conditions model crucial physiological interactions at tissue interfaces. For example, Dirichlet conditions may represent fixed drug concentrations at vascularized boundaries, reflecting controlled drug delivery from blood vessels. Neumann conditions can simulate passive diffusion barriers or controlled release at semi-permeable membranes, while more complex non-local or integral conditions model heterogeneous tissue interactions and active transport mechanisms. By varying these conditions in our simulations, we captured different physiological scenarios such as targeted delivery near vascular structures, diffusion in bounded tissue compartments, and dynamic exchange at tissue interfaces. This exploration supports the biological plausibility of the model and underscores the impact of boundary phenomena on drug distribution within living tissues. Additionally, the simulation results presented in Figure 6 clearly illustrate how varying boundary conditions significantly alters the diffusion patterns within the domain. This numerical evidence supports the biological insight that tissue boundaries, such as membranes, vascular interfaces, or compartment walls, actively influence drug spread by acting as either barriers, reservoirs, or exchange sites. Therefore, our computational exploration of boundary conditions provides both theoretical and practical understanding of their crucial role in predicting drug dynamics in heterogeneous biological environments.

Remark 5.

The choice of kernel function plays a pivotal role in fractional derivative models, as it governs how memory effects and non-local interactions are represented within the system. In this study, we employed a Mittag–Leffler kernel associated with the $\mathsf{\Psi }$–Hilfer fractional derivative. This choice provides substantial modeling flexibility, enabling smooth transitions between classical formulations, such as the Riemann, Liouville, and Caputo derivatives, and effectively capturing anomalous diffusion phenomena in complex and heterogeneous biological media. Nevertheless, we acknowledge that alternative kernel functions, such as power-law kernels, exponential fading memory kernels, and the Caputo–Fabrizio kernel, may be more suitable in certain physical or biological contexts. Each of these kernels encapsulates a distinct memory structure. For instance, power-law kernels are well suited for modeling long-term memory effects; exponential kernels emphasize short-term memory loss; and the Caputo–Fabrizio kernel offers a non-singular, smoothly decaying memory profile. In future work, we intend to extend our model to incorporate these alternative kernels, with the aim of examining their influence on the system’s qualitative behavior. Such investigations may reveal novel dynamical characteristics, improve alignment with empirical data, or enhance computational efficiency, particularly in applications involving drug transport or neuronal dynamics under complex boundary conditions.

4. Conclusions

This study introduced a fractional diffusion model with non-local boundary conditions to describe drug transport in biological tissues, effectively capturing memory effects and long-range interactions. Theoretical analysis and numerical simulations confirmed the model’s capability to reflect key diffusion dynamics influenced by fractional orders, boundary conditions, and initial configurations. Our findings highlight the potential of fractional models as predictive tools for drug delivery optimization in complex biological environments. Future research will focus on extending these results to three-dimensional domains and personalized medicine applications.