The Influence of Lévy Noise and Independent Jumps on the Dynamics of a Stochastic COVID-19 Model with Immune Response and Intracellular Transmission
Abstract
1. Introduction
2. Model Formulation
3. Existence and Uniqueness
- .
- such thatwith , wherewhere denotes the compensated random measure.
- .
- for where C is a positive constant.
4. Extinction
5. Persistence
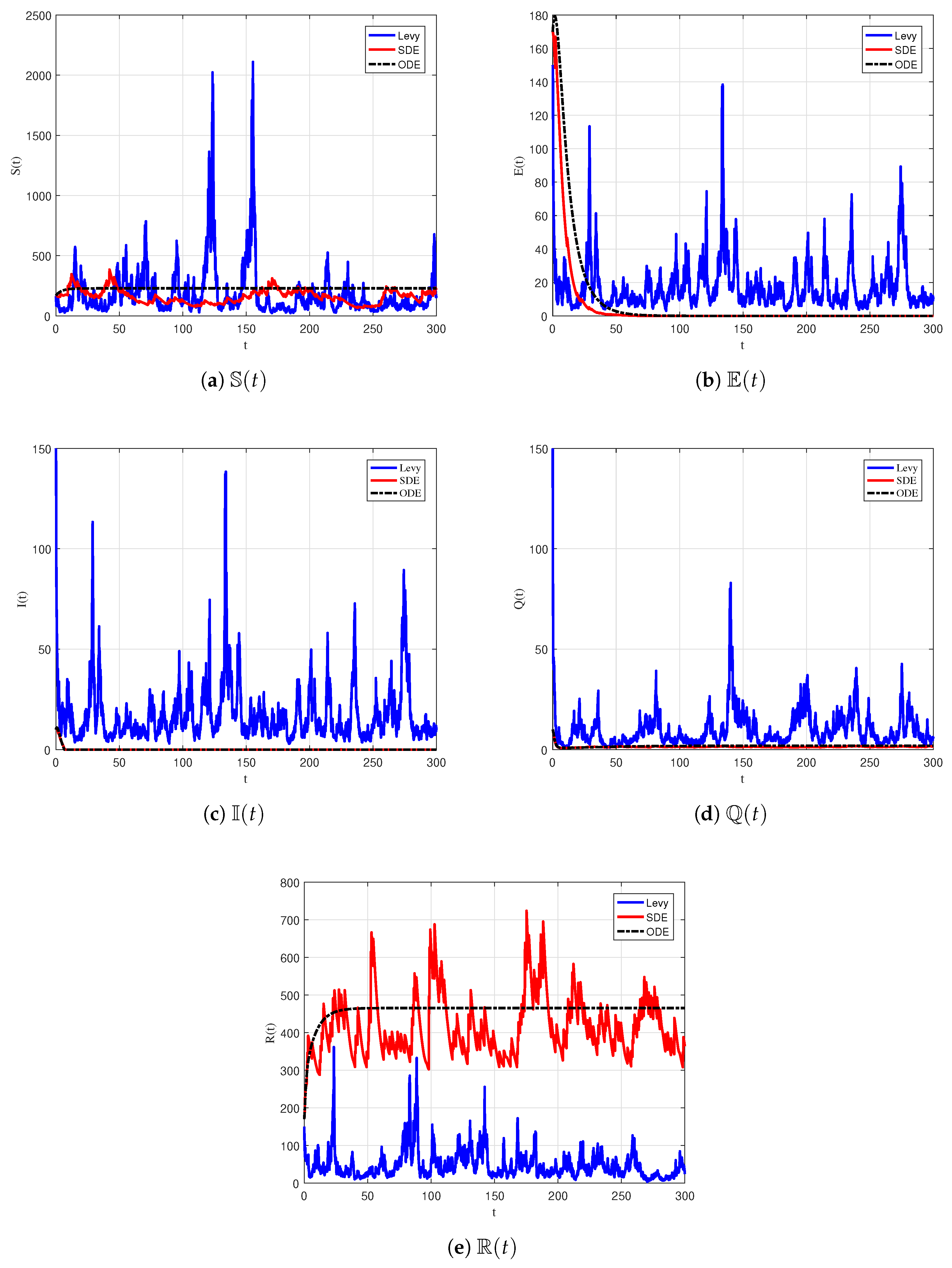
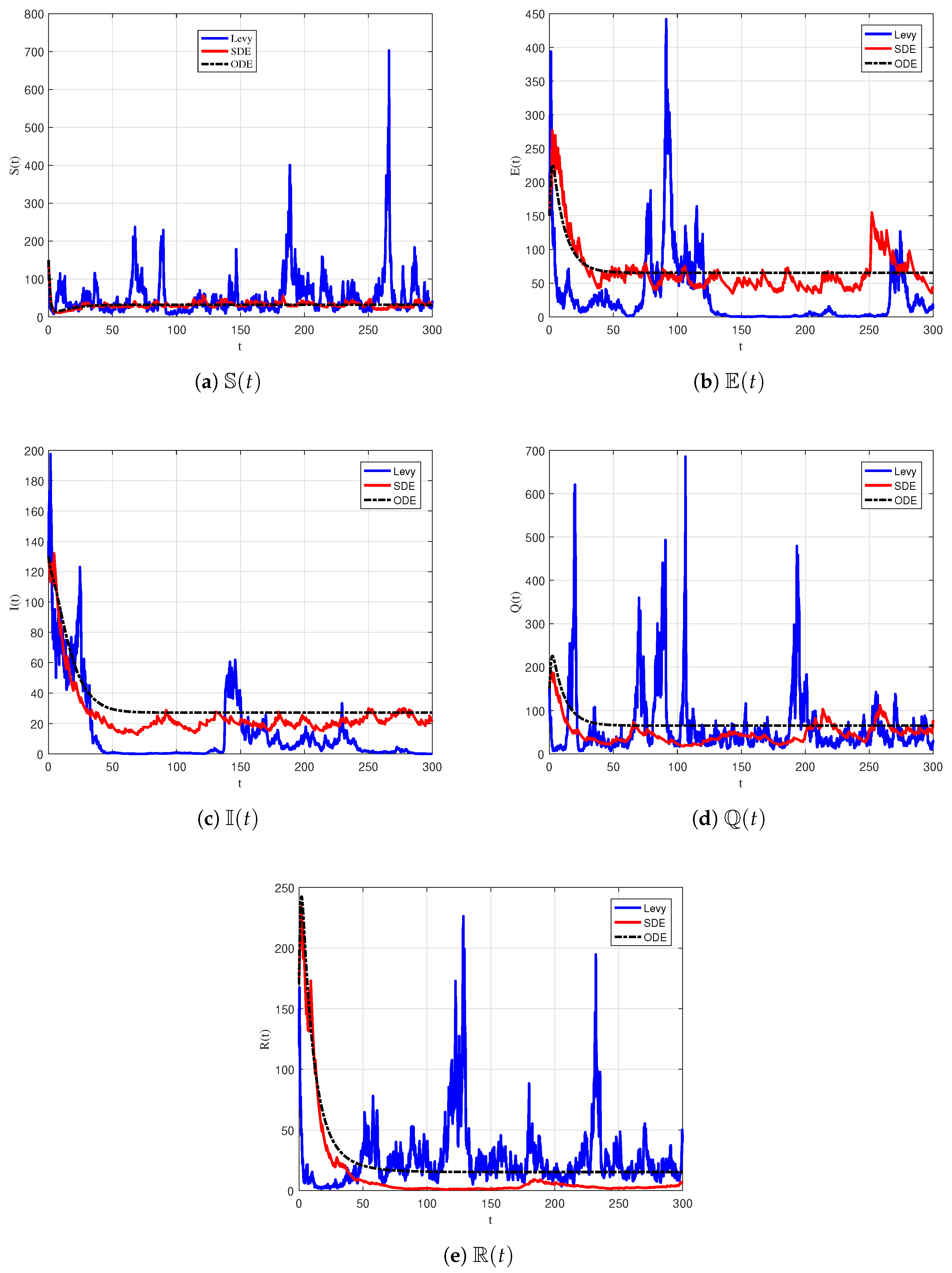
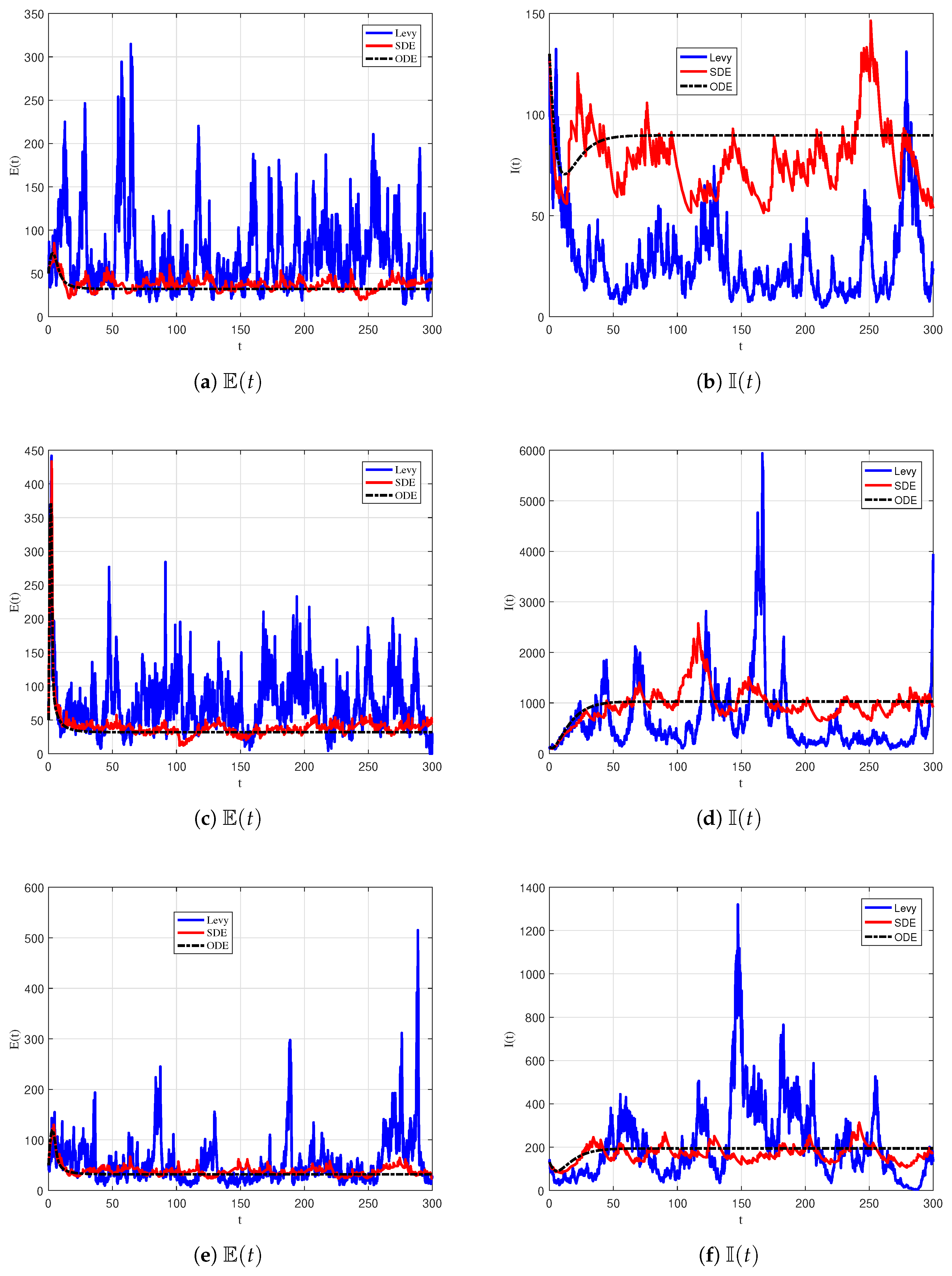
6. Numerical Analysis
6.1. Milstein Scheme with Jumps
6.2. Numerical Simulation of Extinction
6.3. Numerical Simulation of Persistence
6.4. Effects of Lévy Noise
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lai, C.-C.; Shih, T.-P.; Ko, W.-C.; Tang, H.-T.; Hsueh, P.-R. Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) and corona virus disease-2019 (COVID-19): The epidemic and the challenges. Int. J. Antimicrob. Agents 2020, 55, 105924. [Google Scholar] [CrossRef]
- De Groot, R.J.; Baker, S.C.; Baric, R.S.; Brown, C.S.; Drosten, C.; Enjuanes, L.; Fouchier, R.A.M.; Galiano, M.; Gorbalenya, A.E.; Memish, Z.A.; et al. Commentary: Middle East respiratory syndrome coronavirus (MERS-CoV): Announcement of the Coronavirus Study Group. J. Virol. 2013, 87, 7790–7792. [Google Scholar] [CrossRef]
- WHO MERS-CoV Research Group. State of knowledge and data gaps of Middle East respiratory syndrome coronavirus (MERS-CoV) in humans. PLoS Curr. 2013, 5, 1–30. [Google Scholar] [CrossRef]
- Chikungunya, E.C.D.C. Factsheet for Health Professionals. Available online: http://ecdc.europa.eu/en/ (accessed on 1 April 2025).
- World Health Organization. Coronavirus Disease 2019 (COVID-19): Situation Report, 67; World Health Organization: Geneva, Switzerland, 2020. [Google Scholar]
- World Health Organization. Coronavirus Disease 2019 (COVID-19): Situation Report, 85; World Health Organization: Geneva, Switzerland, 2020. [Google Scholar]
- Cao, Z.; Zhu, J.; Wang, Z.; Peng, Y.; Zeng, L. Comprehensive pan-cancer analysis reveals ENC1 as a promising prognostic biomarker for tumor microenvironment and therapeutic responses. Sci. Rep. 2024, 14, 25331. [Google Scholar] [CrossRef]
- Perko, L. Differential Equations and Dynamical Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 7. [Google Scholar]
- Arnold, L. Stochastic Differential Equations; Wiley: Hoboken, NJ, USA, 1974. [Google Scholar]
- Wu, Z.; McGoogan, J.M. Characteristics of and important lessons from the coronavirus disease 2019 (COVID-19) outbreak in China: Summary of a report of 72 314 cases from the Chinese Center for Disease Control and Prevention. JAMA 2020, 323, 1239–1242. [Google Scholar] [CrossRef] [PubMed]
- Sinan, M.; Alharthi, N.H. Mathematical analysis of fractal-fractional mathematical model of COVID-19. Fractal Fract. 2023, 7, 358. [Google Scholar] [CrossRef]
- Khader, M.M.; Adel, M. Modeling and numerical simulation for covering the fractional COVID-19 model using spectral collocation-optimization algorithm. Fractal Fract. 2022, 6, 363. [Google Scholar] [CrossRef]
- Gray, A.; Greenhalgh, D.; Hu, L.; Mao, X.; Pan, J. A stochastic differential equation SIS epidemic model. SIAM J. Appl. Math. 2011, 71, 876–902. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, W.; Yuan, S. Survival and stationary distribution of a SIR epidemic model with stochastic perturbations. Appl. Math. Comput. 2014, 244, 118–131. [Google Scholar] [CrossRef]
- Lu, Q. Stability of SIRS system with random perturbations. Phys. A Stat. Mech. Its Appl. 2009, 388, 3677–3686. [Google Scholar] [CrossRef]
- Ji, C.; Jiang, D. Threshold behaviour of a stochastic SIR model. Appl. Math. Model. 2014, 38, 5067–5079. [Google Scholar] [CrossRef]
- Din, A.; Ain, Q.T. Stochastic optimal control analysis of a mathematical model: Theory and application to non-singular kernels. Fractal Fract. 2022, 6, 279. [Google Scholar] [CrossRef]
- An, X.; Du, L.; Jiang, F.; Zhang, Y.; Deng, Z.; Kurths, J. A few-shot identification method for stochastic dynamical systems based on residual multipeaks adaptive sampling. Chaos Interdiscip. J. Nonlinear Sci. 2024, 34, 073118. [Google Scholar] [CrossRef]
- Ikram, R.; Hussain, G.; Khan, I.; Khan, A.; Zaman, G.; Raezah, A.A. Stationary distribution of stochastic COVID-19 epidemic model with control strategies. AIMS Math. 2024, 9, 30413–30442. [Google Scholar] [CrossRef]
- Shah, S.M.A.; Nie, Y.; Alkhazzan, A.; Tunç, C. A stochastic hepatitis B model with media coverage and Lévy noise. J. Taibah Univ. Sci. 2024, 18, 2414523. [Google Scholar] [CrossRef]
- Din, A.; Li, Y. Lévy noise impact on a stochastic hepatitis B epidemic model under real statistical data and its fractal–fractional Atangana–Baleanu order model. Phys. Scr. 2021, 96, 124008. [Google Scholar] [CrossRef]
- Luzyanina, T.; Bocharov, G. Stochastic modeling of the impact of random forcing on persistent hepatitis B virus infection. Math. Comp. Simul. 2014, 96, 54–65. [Google Scholar] [CrossRef]
- El Fatini, M.; Sekkak, I. Lévy noise impact on a stochastic delayed epidemic model with Crowly–Martin incidence and crowding effect. Phys. A Stat. Mech. Its Appl. 2020, 541, 123315. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, L.; Qiu, Z. Dynamics of a stochastic cholera epidemic model with Lévy process. Phys. A 2022, 595, 127069. [Google Scholar] [CrossRef]
- Zahri, M. Multidimensional Milstein scheme for solving a stochastic model for prebiotic evolution. J. Taibah Univ. Sci. 2014, 8, 186–198. [Google Scholar] [CrossRef]
- Leng, X.N.; Feng, T.; Meng, X.Z. Stochastic inequalities and applications to dynamics analysis of a novel SIVS epidemic model with jumps. J. Inequal. Appl. 2017, 138. [Google Scholar] [CrossRef] [PubMed]
- Danane, J.; Allali, K.; Hammouch, Z.; Nisar, K.S. Mathematical analysis and simulation of a stochastic COVID-19 Lévy jump model with isolation strategy. Results Phys. 2021, 23, 103994. [Google Scholar] [CrossRef] [PubMed]
- Mao, X.; Wei, F.; Wiriyakraikul, T. Positivity preserving truncated Euler–Maruyama method for stochastic Lotka-Volterra competition model. J. Comput. Appl. Math. 2021, 394, 113566. [Google Scholar] [CrossRef]
| Parameter | Description |
|---|---|
| The size of the vulnerable population at time t | |
| Denote the size of the infected individuals at time t which are not yet infectious | |
| Size of the infected compartment at time t | |
| At time t, the quarantined individuals | |
| Recovered individuals at time t | |
| b | Birth rate or recruitment into the susceptible population |
| Transmission rate of the infection | |
| Modification factor accounting for enhanced transmission due to increased contact | |
| Natural mortality rate | |
| Rate of progression from infected to quarantined individuals | |
| Rate of progression from exposed to quarantined individuals | |
| Rate of direct transition from susceptible to quarantined individuals | |
| Rate of natural immunity acquisition from susceptible individuals | |
| Rate of progression from exposed to infectious individuals | |
| Rate of disease-induced mortality in infected individuals | |
| Recovery rate from infection | |
| Transition rate from quarantined to recovered individuals | |
| Total number of individuals at any time t, defined as |
| Parameter | Set 1 | Set 2 |
|---|---|---|
| 500 | 1000 | |
| 20 | 50 | |
| 10 | 30 | |
| 5 | 15 | |
| 0 | 5 | |
| b | 0.02 | 0.03 |
| 0.5 | 0.7 | |
| 0.1 | 0.15 | |
| 0.01 | 0.02 | |
| 0.05 | 0.07 | |
| 0.03 | 0.05 | |
| 0.02 | 0.03 | |
| 0.01 | 0.02 | |
| 0.2 | 0.25 | |
| 0.03 | 0.04 | |
| 0.1 | 0.15 | |
| 0.08 | 0.1 | |
| 535 | 1100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Liu, P.; Din, A. The Influence of Lévy Noise and Independent Jumps on the Dynamics of a Stochastic COVID-19 Model with Immune Response and Intracellular Transmission. Fractal Fract. 2025, 9, 306. https://doi.org/10.3390/fractalfract9050306
Song Y, Liu P, Din A. The Influence of Lévy Noise and Independent Jumps on the Dynamics of a Stochastic COVID-19 Model with Immune Response and Intracellular Transmission. Fractal and Fractional. 2025; 9(5):306. https://doi.org/10.3390/fractalfract9050306
Chicago/Turabian StyleSong, Yuqin, Peijiang Liu, and Anwarud Din. 2025. "The Influence of Lévy Noise and Independent Jumps on the Dynamics of a Stochastic COVID-19 Model with Immune Response and Intracellular Transmission" Fractal and Fractional 9, no. 5: 306. https://doi.org/10.3390/fractalfract9050306
APA StyleSong, Y., Liu, P., & Din, A. (2025). The Influence of Lévy Noise and Independent Jumps on the Dynamics of a Stochastic COVID-19 Model with Immune Response and Intracellular Transmission. Fractal and Fractional, 9(5), 306. https://doi.org/10.3390/fractalfract9050306







