FPGA Implementation of Secure Image Transmission System Using 4D and 5D Fractional-Order Memristive Chaotic Oscillators
Abstract
1. Introduction
- (i)
- The hardware implementation of fractional-order chaotic oscillators based on 4D and 5D memristive systems, realized on FPGA using EFORK method for iterative approximation of system trajectories in VHSIC Hardware Description Language (VHDL).
- (ii)
- The synchronization of two identical fractional-order chaotic oscillators based on memristive systems in a master–slave topology using Hamiltonian form and observer approach to facilitate secure information transmission, with digital implementations on an Artix-7 AC701 (AMD, Santa Clara, CA, USA) evaluation board.
- (iii)
- The modular design of transmitter–receiver architecture integrating observer-based synchronization and a multi-stage image encryption pipeline fully implemented in hardware.
2. Preliminaries
2.1. Fractional Calculus
2.2. Explicit Fractional-Order Runge Kutta (EFORK) Numerical Method
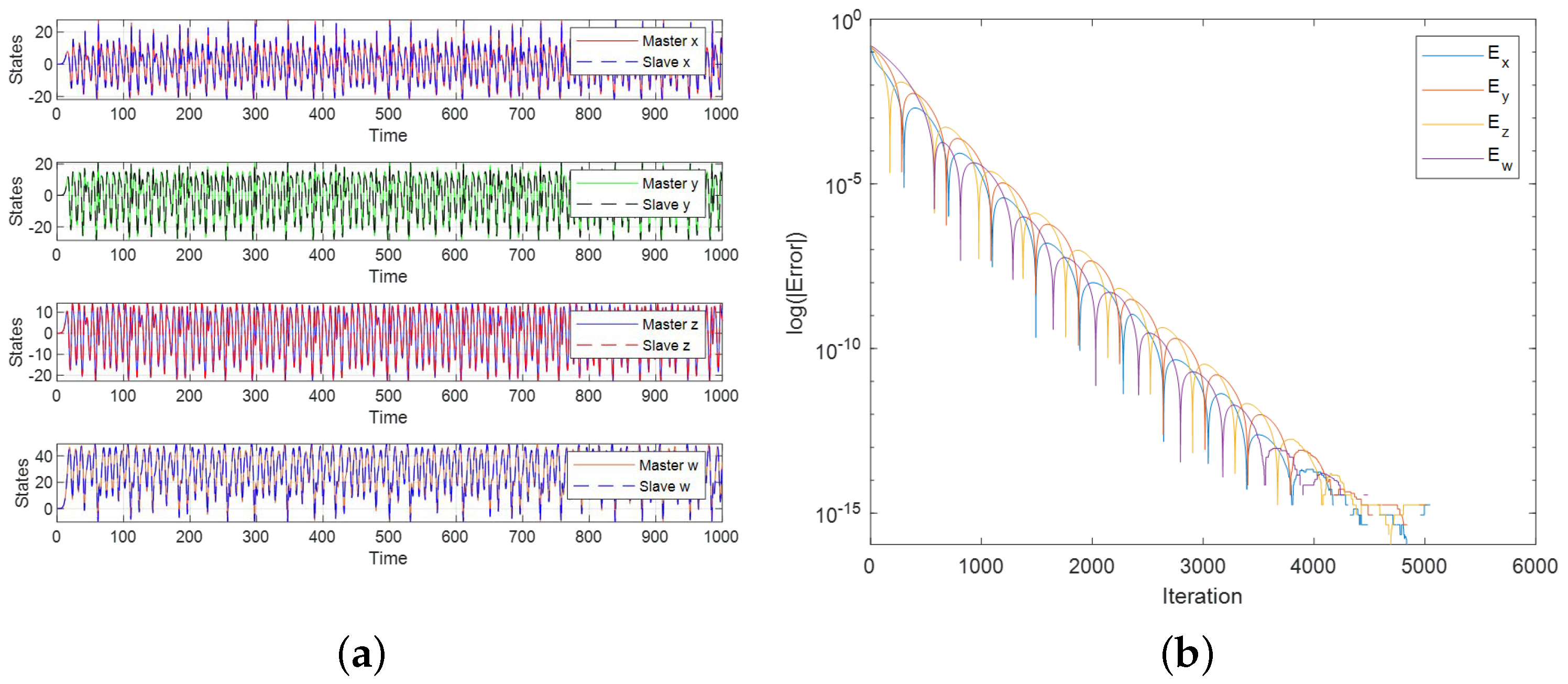
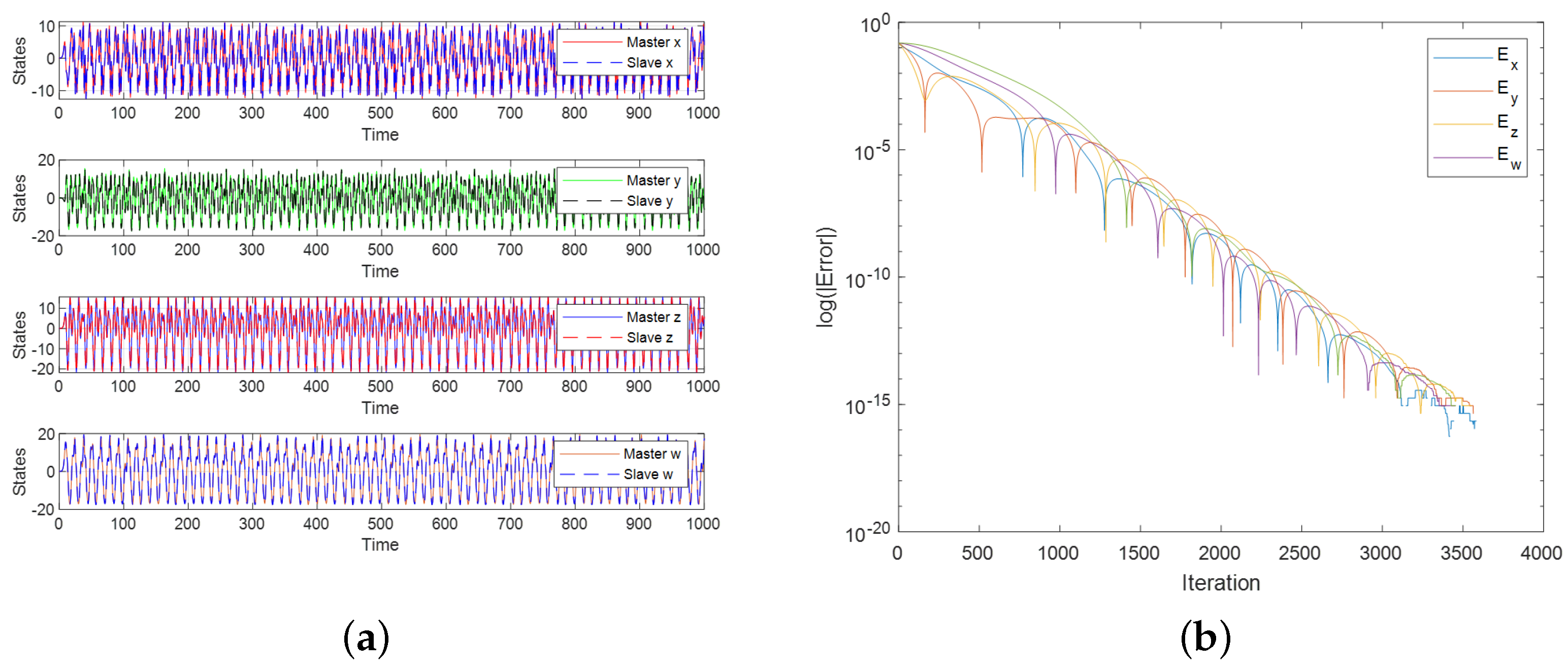
2.3. Hamiltonian Form and Observer Synchronization of Chaotic Systems
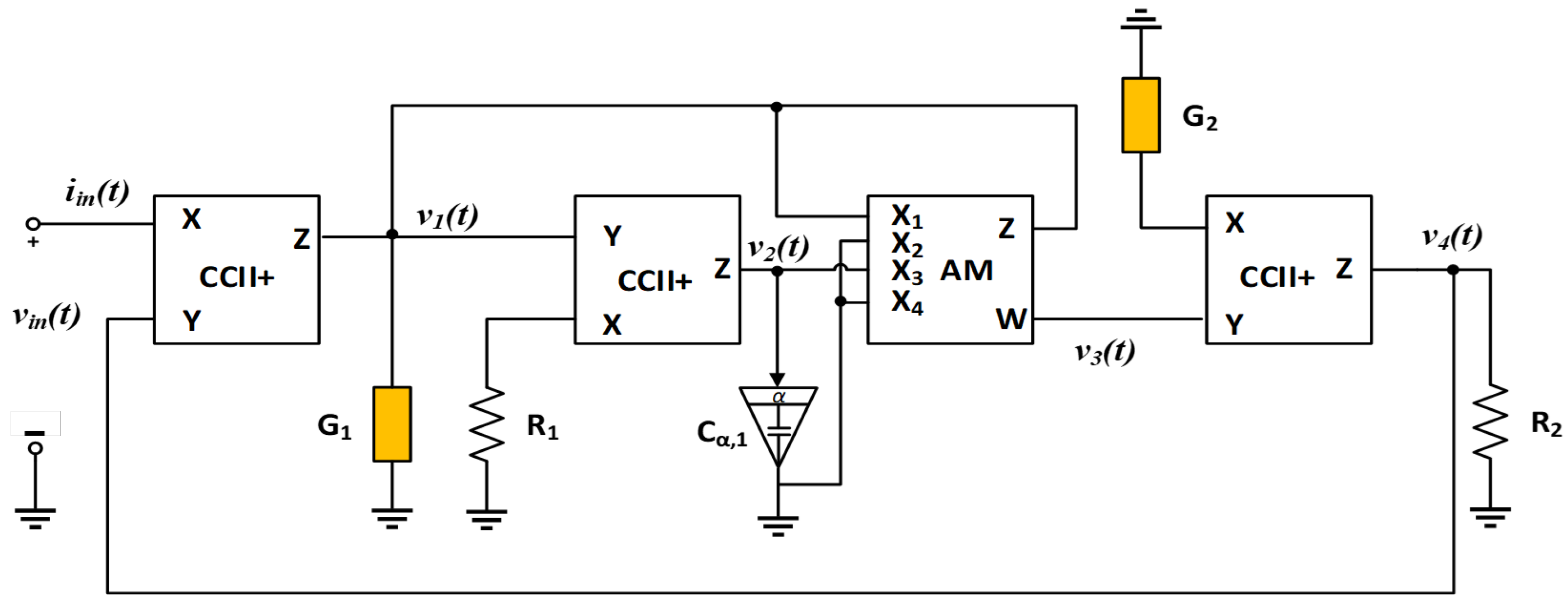
3. Fractional-Order Universal Memristive Systems
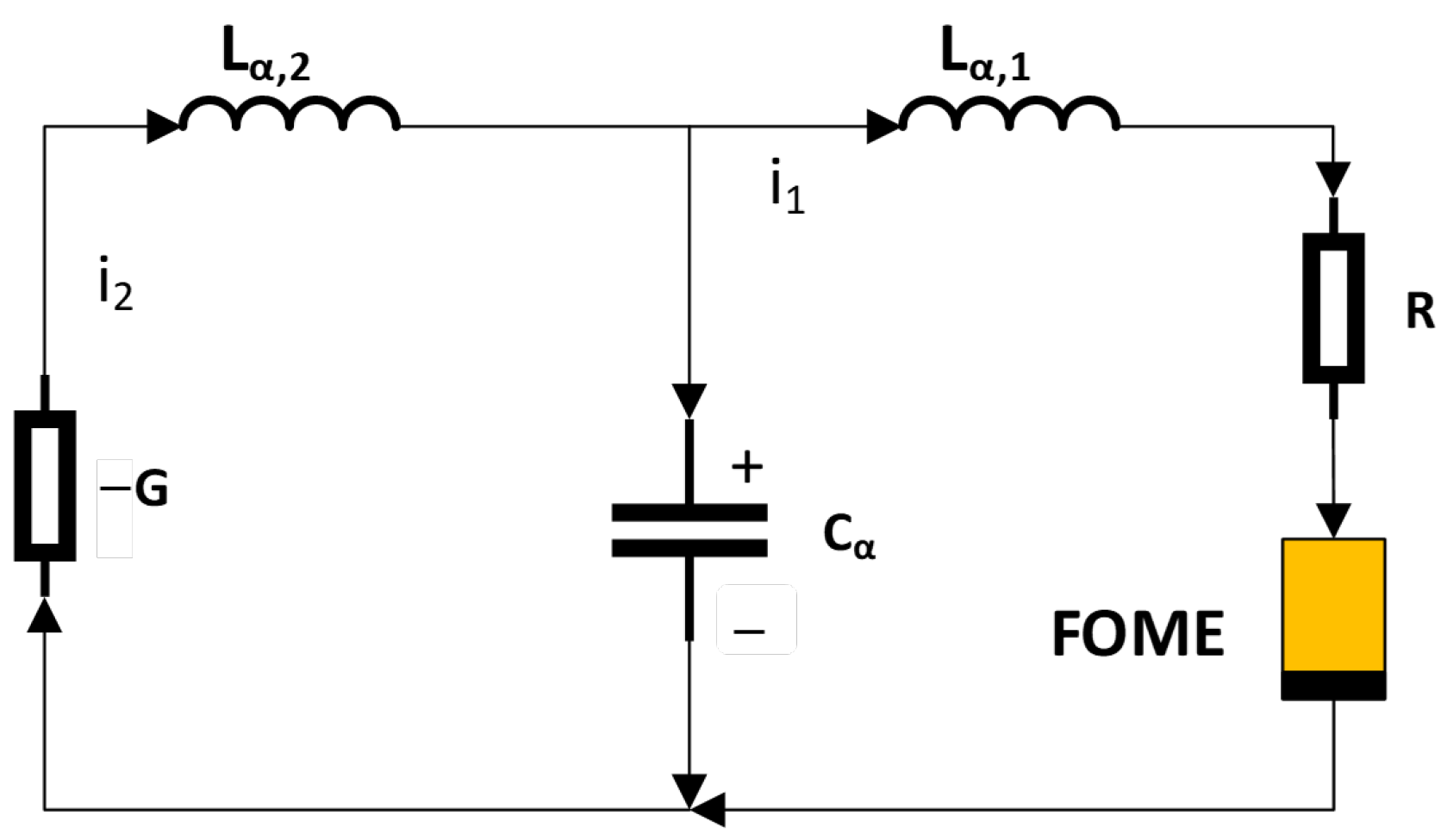
3.1. Reconfigurable Memristive Emulator Circuit of Arbitrary Order
3.2. A New Fractional-Order Model of Universal Memristive Chaotic System
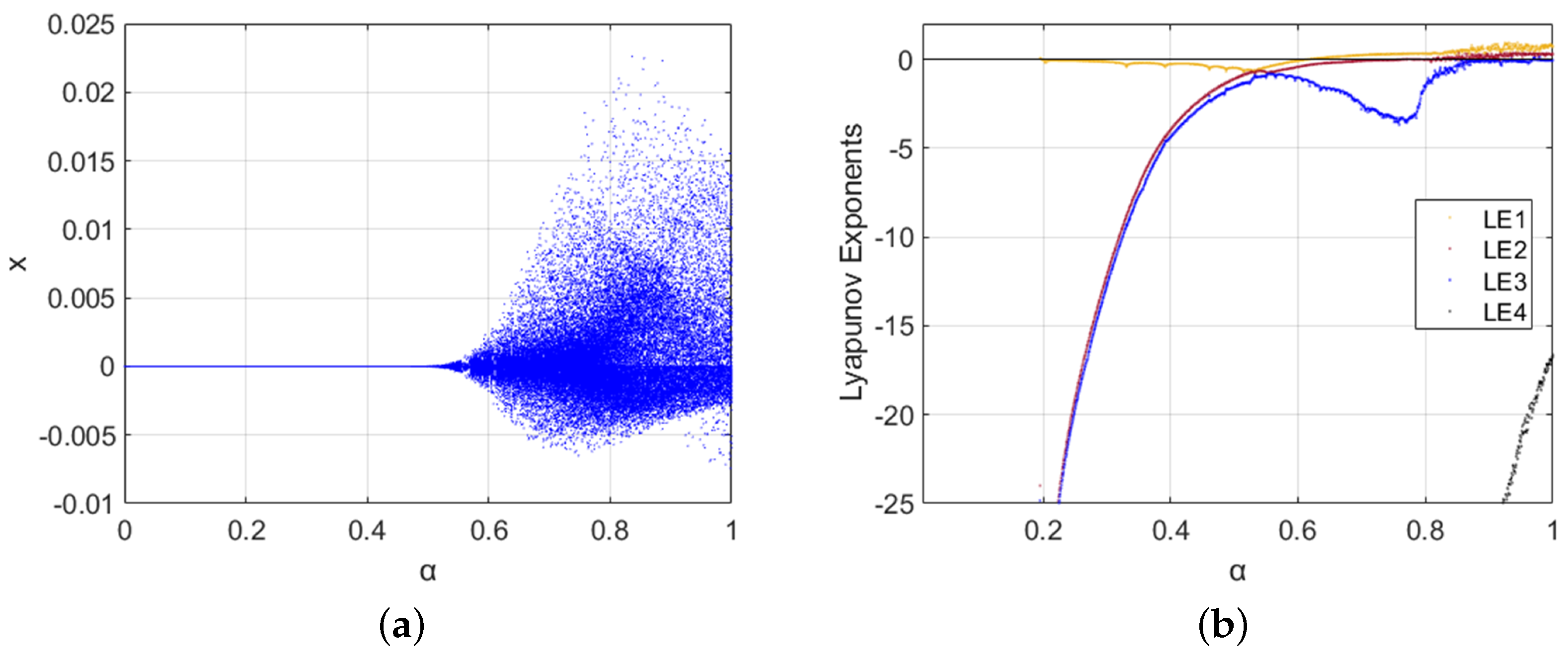
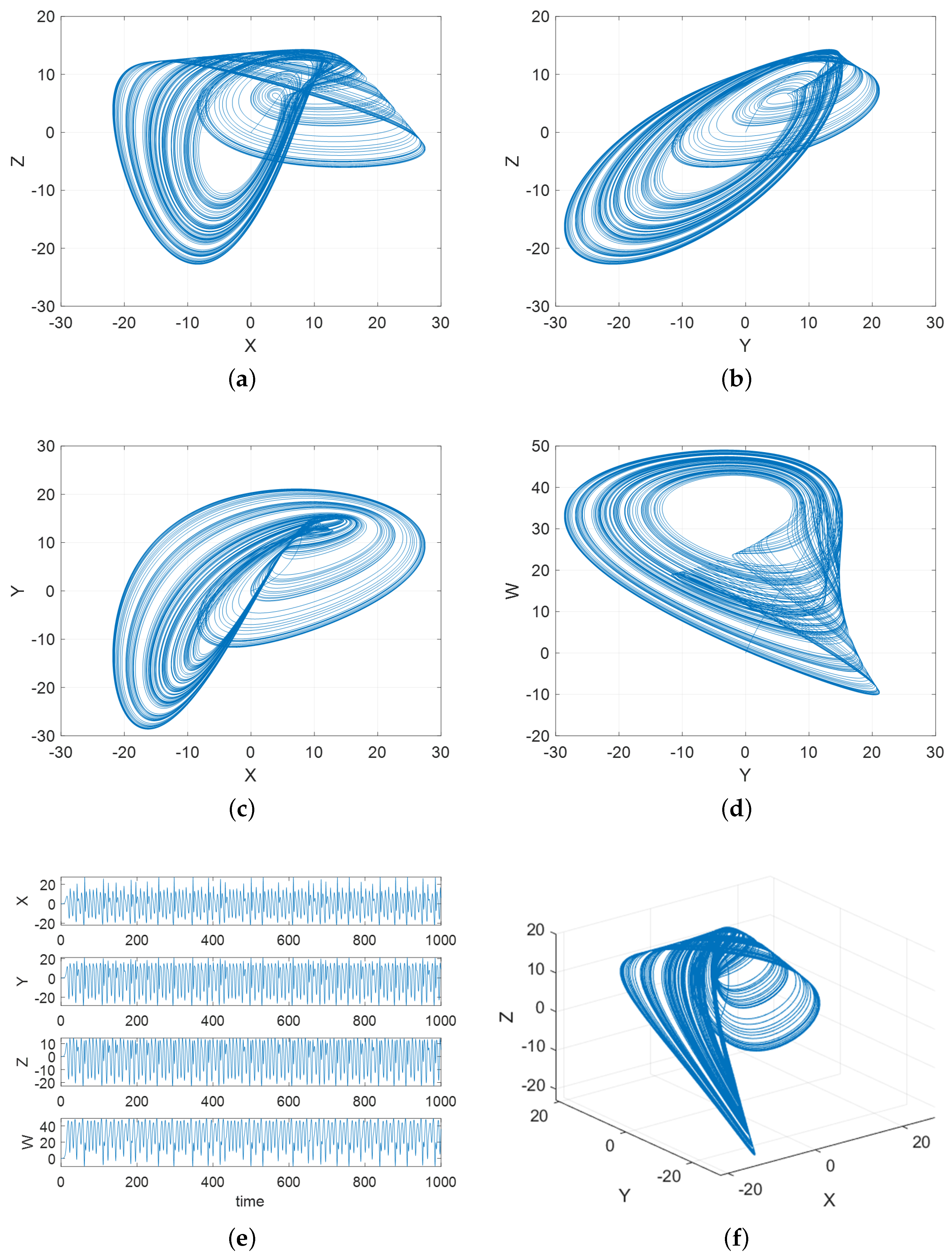
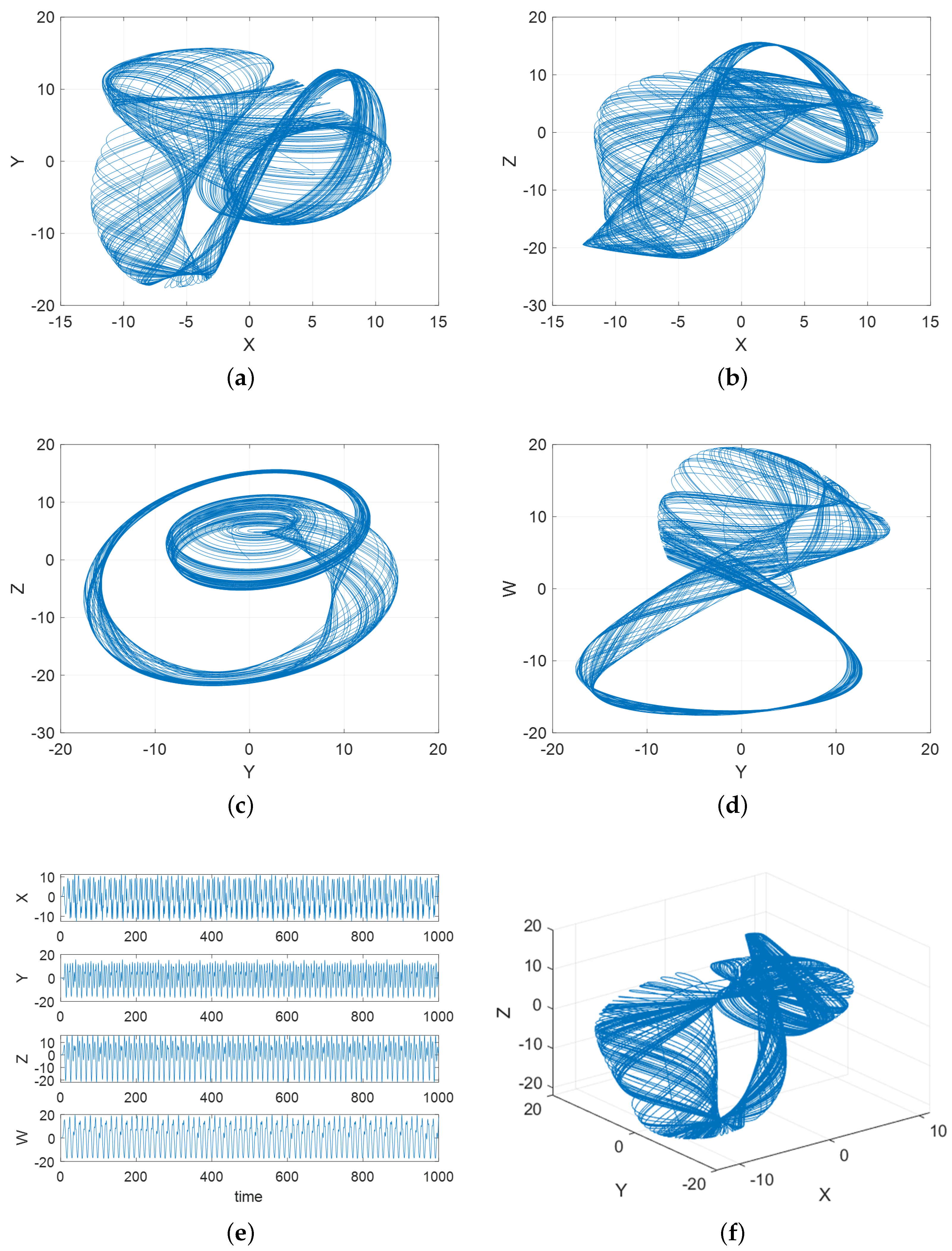
3.3. 4D Memristive Fractional-Order Chaotic System
3.4. 5D Memristive Fractional-Order Chaotic System
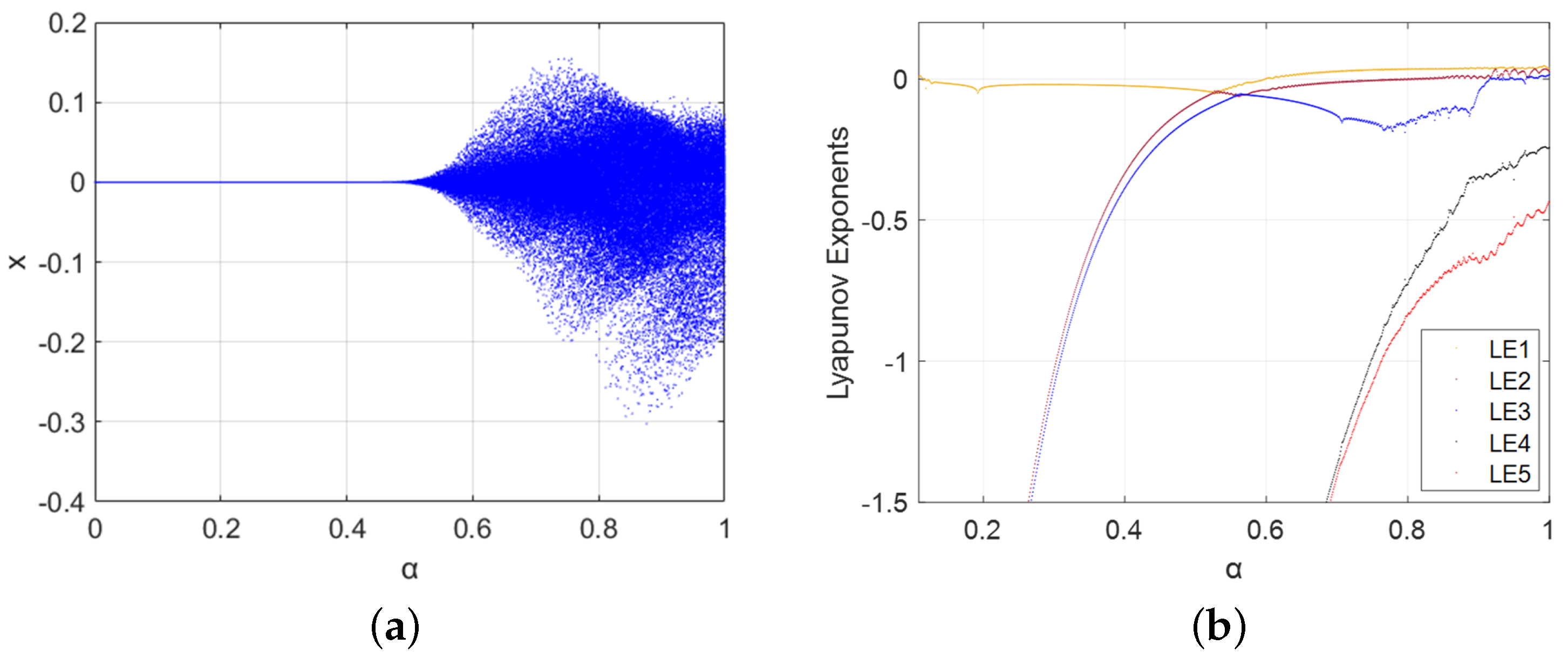
3.5. Synchronization Analysis of 4D and 5D Systems
4. Proposed Image Encryption and Decryption Processes
4.1. Chaotic Permutation via Dynamic Index Mapping
- Chaotic Index Selection: For each position , two chaotic values and are extracted cyclically, where ℓ is the length of the chaotic sequences and “mod” represents the modulo operation. A dynamic salt value is computed as Equation (43),where denotes the dynamic feedback value initialized to a fixed integer constant.
- Random Position Mapping: A candidate index is then selected via Equation (44),
- Feedback Update: The feedback is updated iteratively according to Equation (46),which introduces inter-dependence across pixels, making sure that even little changes in the image or chaotic inputs result in a completely different permutation pattern. The final result is a permuted image vector , where both pixel positions and values are tightly coupled to the synchronized chaotic sequences and the feedback mechanism.
4.2. Chaotic Bidirectional Diffusion
4.2.1. Forward Diffusion
- Chaotic Rotation: The 8-bit binary representation of is circularly shifted to the left by using Equation (47),where is the third state variable from the 4D chaotic system at index i.
- XOR with Feedback and Chaotic Value: The rotated value is converted back to an integer, then used to diffuse the permuted pixels using two XOR operations according to Equation (48),where is the result of the previous diffusion iteration, and is the rotated integer. The initial forward feedback is set as Equation (49),
4.2.2. Backward Diffusion
- Chaotic Rotation: A rotation is applied using the 5D system according to Equation (50),XOR with Feedback and Chaotic Value: The backward diffused pixel values are then obtained according to Equation (51),where is the rotated version of , and is the backward diffusion value from the next index. The initial backward feedback is defined as Equation (52),
4.2.3. Targeted Bit-Flip and Final Mask Operation
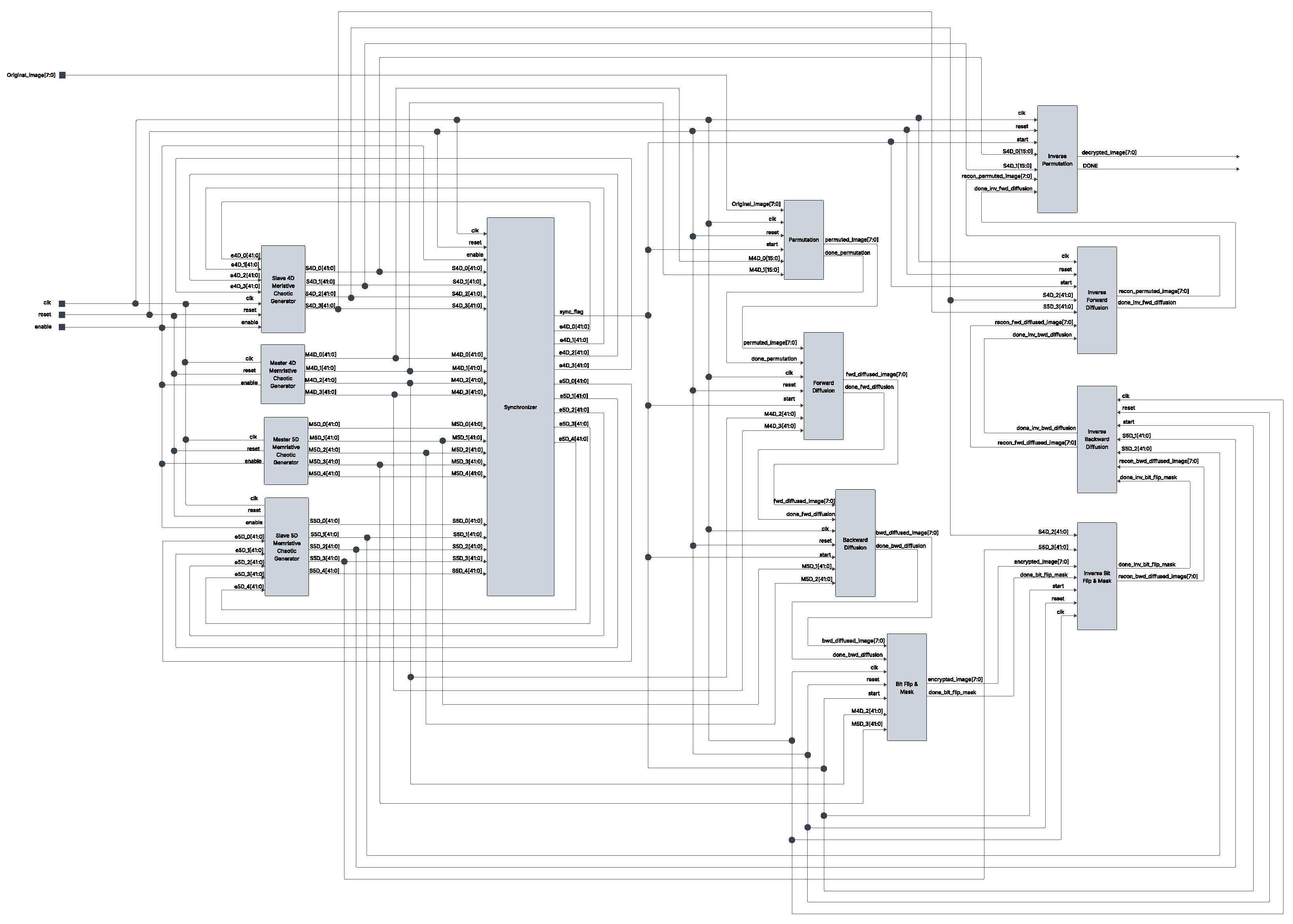
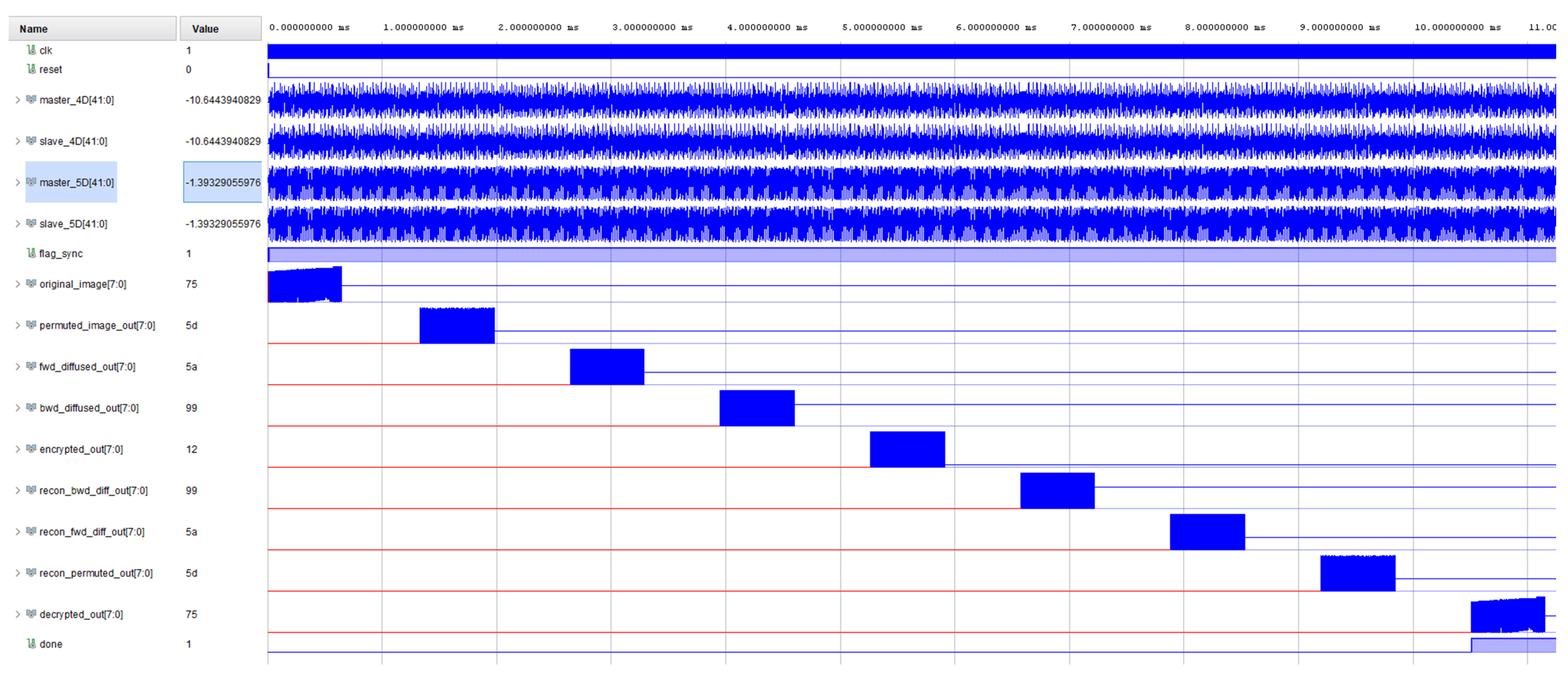
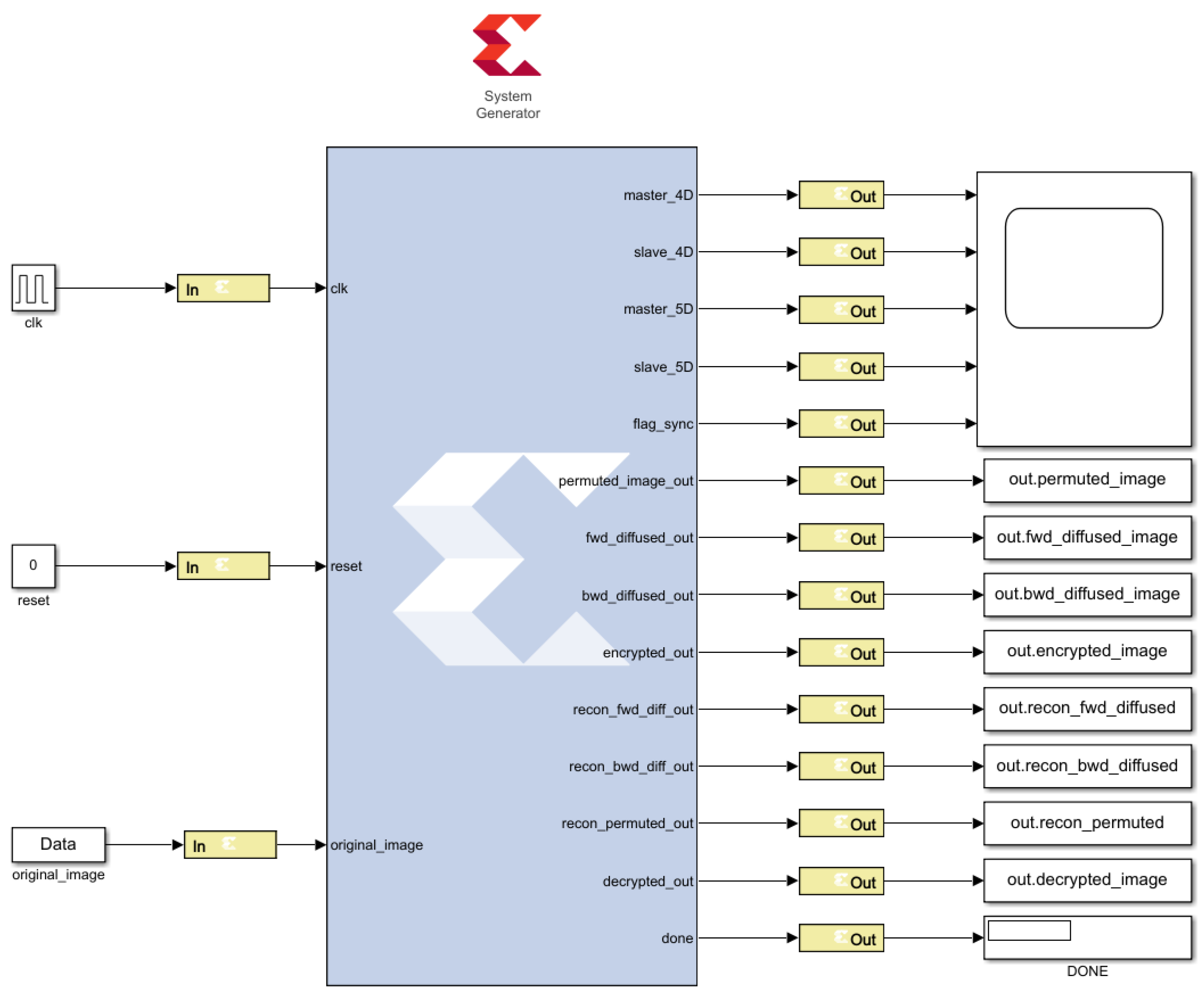
5. FPGA Implementation of Secure Image Transmission System
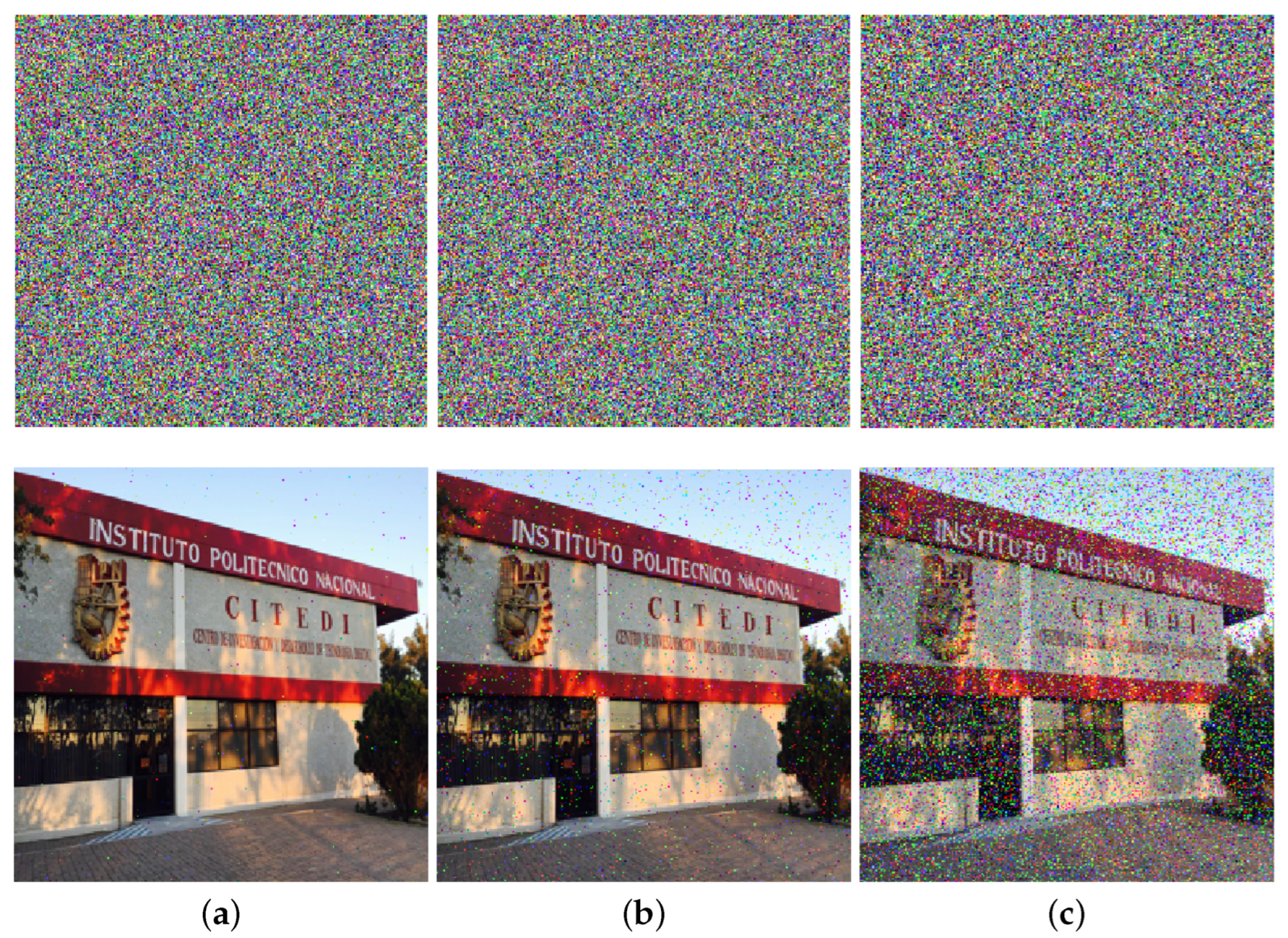
6. Security Analysis
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AM | Analog multiplier |
| BRAM | Block random access memory |
| BUFG | Global clock buffer |
| DSP | Digital signal processor |
| EFORK | Explicit fractional-order Runge–Kutta |
| FC | Fractional calculus |
| FF | Flip flop |
| FOC | Fractional-order capacitor |
| FPGA | Field programmable gate array |
| FSM | Finite-state machine |
| HDL | Hardware description language |
| IO | Input–output |
| LUT | Look up table |
| N/A | Not available |
| PQC | Post-quantum cryptography |
| RGB | Red green blue |
| RSA | Rivest–Shamir–Adleman |
| VHDL | Very high-speed integrated circuit hardware description language |
References
- Ye, C.; Tan, S.; Wang, J.; Shi, L.; Zuo, Q.; Feng, W. Social Image Security with Encryption and Watermarking in Hybrid Domains. Entropy 2025, 27, 276. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, G. Review of Research on Storage Development. Scalable Comput. Pract. Exp. 2021, 22, 365–385. [Google Scholar] [CrossRef]
- Adeyemi, V.A.; Tlelo-Cuautle, E.; Sandoval-Ibarra, Y.; Nuñez-Perez, J.C. FPGA Implementation of Parameter-Switching Scheme to Stabilize Chaos in Fractional Spherical Systems and Usage in Secure Image Transmission. Fractal Fract. 2023, 7, 440. [Google Scholar] [CrossRef]
- Hamidouche, B.; Guesmi, K.; Essounbouli, N. Mastering chaos: A review. Annu. Rev. Control 2024, 58, 100966. [Google Scholar] [CrossRef]
- Montero-Canela, R.; Zambrano-Serrano, E.; Tamariz-Flores, E.I.; Muñoz-Pacheco, J.M.; Torrealba-Meléndez, R. Fractional chaos based-cryptosystem for generating encryption keys in Ad Hoc networks. Ad Hoc Netw. 2020, 97, 102005. [Google Scholar] [CrossRef]
- Lai, Q.; Yang, L.; Liu, Y. Design and realization of discrete memristive hyperchaotic map with application in image encryption. Chaos Solitons Fractals 2022, 165, 112781. [Google Scholar] [CrossRef]
- Boutros, A.; Betz, V. FPGA Architecture: Principles and Progression. IEEE Circuits Syst. Mag. 2021, 21, 4–29. [Google Scholar] [CrossRef]
- Pan, G.; Li, C.; Liu, W.; Xue, Y.; Qi, X. Countless coexisting chaotic attractors: From system construction to FPGA-based observation. Chaos Solitons Fractals 2025, 198, 116610. [Google Scholar] [CrossRef]
- Almutairi, N.; Saber, S. Existence of chaos and the approximate solution of the Lorenz–Lü–Chen system with the Caputo fractional operator. AIP Adv. 2024, 14, 015112. [Google Scholar] [CrossRef]
- Clemente-López, D.; Munoz-Pacheco, J.M.; de Jesus Rangel-Magdaleno, J. A Review of the Digital Implementation of Continuous-Time Fractional-Order Chaotic Systems Using FPGAs and Embedded Hardware. Arch. Comput. Methods Eng. 2023, 30, 951–983. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, W.; Sun, K.; Wang, H. Sine-modulation Discrete Memristor Chaotic Map and Its Applications. Nonlinear Dyn. 2025. [Google Scholar] [CrossRef]
- Bao, B.; Rong, K.; Li, H.; Li, K.; Hua, Z.; Zhang, X. Memristor-Coupled Logistic Hyperchaotic Map. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2992–2996. [Google Scholar] [CrossRef]
- Tang, J.; Pan, X.; Chen, X.; Jiang, B.; Li, X.; Pan, J.; Qu, H.; Huang, Z.; Wang, P.; Duan, J.; et al. Flexible Memristor Based on Lead-Free Cs 2 AgBiBr 6 Perovskite for Artificial Nociceptors and Information Security. Adv. Funct. Mater. 2025, 35, 2412375. [Google Scholar] [CrossRef]
- Ye, J.; Chen, B.; Xu, N.; Zhou, J.; Mu, R.; Du, C.; Lu, W.D. A Non-Linear Partial Differential Equation Solver Based on Analog Memristor Crossbar Arrays. IEEE J. Electron Devices Soc. 2025, 13, 477–484. [Google Scholar] [CrossRef]
- Fatemieh, S.E.; Bagheralmoosavi, B.; Reshadinezhad, M.R. Energy-efficient and fast memristor-based serial multipliers applicable in image processing. Results Eng. 2025, 25, 104013. [Google Scholar] [CrossRef]
- Ismail, M.; Na, H.; Rasheed, M.; Mahata, C.; Kim, Y.; Kim, S. Synaptic metaplasticity and associative learning in low-power neuromorphic computing using W-diffused BaTiO3 memristors. Nano Energy 2025, 142, 111276. [Google Scholar] [CrossRef]
- Qian, K.; Xiao, Y.; Wei, Y.; Liu, D.; Wang, Q.; Feng, W. A Robust Memristor-Enhanced Polynomial Hyper-Chaotic Map and Its Multi-Channel Image Encryption Application. Micromachines 2023, 14, 2090. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, S.; Su, D.; Wu, Y.; Gracia, Y.M.; Yin, H. Dynamic Analysis and Implementation of FPGA for a New 4D Fractional-Order Memristive Hopfield Neural Network. Fractal Fract. 2025, 9, 115. [Google Scholar] [CrossRef]
- Hong, Q.; Jiang, H.; Xiao, P.; Du, S.; Li, T. A Parallel Computing Scheme Utilizing Memristor Crossbars for Fast Corner Detection and Rotation Invariance in the ORB Algorithm. IEEE Trans. Comput. 2025, 74, 996–1010. [Google Scholar] [CrossRef]
- Xiao, P.; Fang, J.; Wei, Z.; Dong, Y.; Du, S.; Wen, S.; Hong, Q. A Riccati Matrix Equation Solver Design Based Neurodynamics Method and Its Application. IEEE Trans. Autom. Sci. Eng. 2025, 22, 15163–15176. [Google Scholar] [CrossRef]
- Gokyildirim, A.; Calgan, H.; Demirtas, M. Fractional-Order sliding mode control of a 4D memristive chaotic system. J. Vib. Control 2024, 30, 1604–1620. [Google Scholar] [CrossRef]
- Lai, Q.; Zhu, C.; Qin, M.; Wan, Z. Complex dynamics and encryption application of a 3D dual-memristor oscillatory hyperchaotic map. Math. Comput. Simul. 2025, 236, 270–283. [Google Scholar] [CrossRef]
- Sah, M.; Jin, P.; Wang, G.; Yuan, F.; Fu, H. The Integral Role of Coupling Memristors in Complex Firing Patterns. Int. J. Bifurc. Chaos 2025, 35, 2530022. [Google Scholar] [CrossRef]
- Kundale, S.S.; Kamble, G.U.; Patil, P.P.; Patil, S.L.; Rokade, K.A.; Khot, A.C.; Nirmal, K.A.; Kamat, R.K.; Kim, K.H.; An, H.M.; et al. Review of Electrochemically Synthesized Resistive Switching Devices: Memory Storage, Neuromorphic Computing, and Sensing Applications. Nanomaterials 2023, 13, 1879. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y.; Tang, J.; Li, X.; Gao, B.; Qian, H.; Wu, H. Dynamic memristor-based reservoir computing for high-efficiency temporal signal processing. Nat. Commun. 2021, 12, 408. [Google Scholar] [CrossRef]
- Zhang, G.; Qin, J.; Zhang, Y.; Gong, G.; Xiong, Z.; Ma, X.; Lv, Z.; Zhou, Y.; Han, S. Functional Materials for Memristor-Based Reservoir Computing: Dynamics and Applications. Adv. Funct. Mater. 2023, 33, 2302929. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, X.; Cheng, H.; Qiu, J.; Liu, X.; Wang, M.; Liu, Q. Emerging dynamic memristors for neuromorphic reservoir computing. Nanoscale 2022, 14, 289–298. [Google Scholar] [CrossRef]
- Gokyildirim, A.; Yesil, A.; Babacan, Y. Implementation of a memristor-based 4D chaotic oscillator and its nonlinear control. Analog. Integr. Circuits Signal Process. 2022, 110, 91–104. [Google Scholar] [CrossRef]
- Machado, J.T.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef]
- İbrahim Ethem Saçu. Effects of high-order interactions on synchronization of a fractional-order neural system. Cogn. Neurodyn. 2024, 18, 1877–1893. [Google Scholar] [CrossRef]
- Abu-Shady, M.; Kaabar, M.K.A. A Generalized Definition of the Fractional Derivative with Applications. Math. Probl. Eng. 2021, 2021, 1–9. [Google Scholar] [CrossRef]
- Albadarneh, R.B.; Batiha, I.M.; Adwai, A.; Tahat, N.; Alomari, A.K. Numerical approach of riemann-liouville fractional derivative operator. Int. J. Electr. Comput. Eng. (IJECE) 2021, 11, 5367. [Google Scholar] [CrossRef]
- Sousa, J.V.D.C.; de Oliveira, E.C. On the Ψ-Hilfer fractional derivative. Commun. Nonlinear Sci. Numer. Simul. 2018, 60, 72–91. [Google Scholar] [CrossRef]
- Ma, L.; Li, C. On Hadamard Fractional Calculus. Fractals 2017, 25, 1750033. [Google Scholar] [CrossRef]
- Tarasov, V.E. General Fractional Calculus in Multi-Dimensional Space: Riesz Form. Mathematics 2023, 11, 1651. [Google Scholar] [CrossRef]
- Raza, N.; Raza, A.; Ullah, M.A.; Gómez-Aguilar, J.F. Modeling and investigating the spread of COVID-19 dynamics with Atangana-Baleanu fractional derivative: A numerical prospective. Phys. Scr. 2024, 99, 035255. [Google Scholar] [CrossRef]
- Jin, B. Fractional Differential Equations; Springer International Publishing: Berlin/Heidelberg, Germany, 2021; Volume 206. [Google Scholar] [CrossRef]
- Baliarsingh, P.; Nayak, L. Fractional Derivatives with Variable Memory. Iran. J. Sci. Technol. Trans. A Sci. 2022, 46, 849–857. [Google Scholar] [CrossRef]
- Lekshmi, A.S.; Balakumar, V. Numerical investigation of fractional order chaotic systems using a new modified Runge-Kutta method. Phys. Scr. 2024, 99, 105225. [Google Scholar] [CrossRef]
- Ghoreishi, F.; Ghaffari, R.; Saad, N. Fractional Order Runge–Kutta Methods. Fractal Fract. 2023, 7, 245. [Google Scholar] [CrossRef]
- Xu, S.; Wang, X.; Ye, X. A new fractional-order chaos system of Hopfield neural network and its application in image encryption. Chaos Solitons Fractals 2022, 157, 111889. [Google Scholar] [CrossRef]
- Al-Barakati, A.A.; Mesdoui, F.; Bekiros, S.; Kaçar, S.; Jahanshahi, H. A variable-order fractional memristor neural network: Secure image encryption and synchronization via a smooth and robust control approach. Chaos Solitons Fractals 2024, 186, 115135. [Google Scholar] [CrossRef]
- Khan, N.A.; Qureshi, M.A.; Khan, N.A. Evolving Tangent Hyperbolic memristor based 6D chaotic model with fractional order derivative: Analysis and applications. Partial Differ. Equ. Appl. Math. 2023, 7, 100505. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, K.; Zhang, J.; Zhao, X.; Chen, Y.; Cai, B.; Zhu, Z.; Wen, H.; Ye, C. Integrating Fractional-Order Hopfield Neural Network with Differentiated Encryption: Achieving High-Performance Privacy Protection for Medical Images. Fractal Fract. 2025, 9, 426. [Google Scholar] [CrossRef]
- Mohamed, S.M.; Sayed, W.S.; Madian, A.H.; Radwan, A.G.; Said, L.A. An Encryption Application and FPGA Realization of a Fractional Memristive Chaotic System. Electronics 2023, 12, 1219. [Google Scholar] [CrossRef]
- Yousefpour, A.; Jahanshahi, H.; Munoz-Pacheco, J.M.; Bekiros, S.; Wei, Z. A fractional-order hyper-chaotic economic system with transient chaos. Chaos Solitons Fractals 2020, 130, 109400. [Google Scholar] [CrossRef]
- Shafiq, F.; Malik, M. Fractional Derivatives with Applications: A Review. Math. Sci. Appl. 2023, 2, 33–50. [Google Scholar]
- Roldán-Caballero, A.; Pérez-Cruz, J.H.; Hernández-Márquez, E.; García-Sánchez, J.R.; Ponce-Silva, M.; de Jesus Rubio, J.; Villarreal-Cervantes, M.G.; Martínez-Martínez, J.; García-Trinidad, E.; Mendoza-Chegue, A. Synchronization of a New Chaotic System Using Adaptive Control: Design and Experimental Implementation. Complexity 2023, 2023, 1–22. [Google Scholar] [CrossRef]
- Fujisaka, H.; Yamada, T. Stability Theory of Synchronized Motion in Coupled-Oscillator Systems. Prog. Theor. Phys. 1983, 69, 32–47. [Google Scholar] [CrossRef]
- Chen, L.Q.; Liu, Y.Z. An Open-Plus-Closed-Loop Approach To Synchronization of Chaotic And Hyperchaotic Maps. Int. J. Bifurc. Chaos 2002, 12, 1219–1225. [Google Scholar] [CrossRef]
- Hoon, Y.; Radzi, M.A.M.; Zainuri, M.A.A.M.; Zawawi, M.A.M. Shunt Active Power Filter: A Review on Phase Synchronization Control Techniques. Electronics 2019, 8, 791. [Google Scholar] [CrossRef]
- Li, C.; Liao, X.; wo Wong, K. Lag synchronization of hyperchaos with application to secure communications. Chaos Solitons Fractals 2005, 23, 183–193. [Google Scholar] [CrossRef]
- Sira-Ramírez, H.; Cruz-Hernández, C. Synchronization Of Chaotic Systems: A Generalized Hamiltonian Systems Approach. Int. J. Bifurc. Chaos 2001, 11, 1381–1395. [Google Scholar] [CrossRef]
- Estudillo-Valdez, M.A.; Adeyemi, V.A.; Tlelo-Cuautle, E.; Sandoval-Ibarra, Y.; Nuñez-Perez, J.C. FPGA realization of four chaotic interference cases in a terrestrial trajectory model and application in image transmission. Sci. Rep. 2023, 13, 12969. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, C.; Zhang, X. A universal emulator for memristor, memcapacitor, and meminductor and its chaotic circuit. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 013141. [Google Scholar] [CrossRef]
- Koçak, H.; Palmer, K.J. Lyapunov Exponents and Sensitive Dependence. J. Dyn. Differ. Equ. 2010, 22, 381–398. [Google Scholar] [CrossRef]
- Yue, W.; Noonan, J.P.; Agaian, S. NPCR and UACI Randomness Tests for Image Encryption. J. Sel. Areas Telecommun. 2011, 1, 31–38. [Google Scholar]
- Liu, J.; Li, R.; Huang, D. Stability, bifurcation and characteristics of chaos in a new commensurate and incommensurate fractional-order ecological system. Math. Comput. Simul. 2025, 236, 248–269. [Google Scholar] [CrossRef]
- Li, Y.; Li, C.; Li, Y.; Moroz, I.; Yang, Y. A joint image encryption based on a memristive Rulkov neuron with controllable multistability and compressive sensing. Chaos Solitons Fractals 2024, 182, 114800. [Google Scholar] [CrossRef]
- Man, Z.; Li, J.; Di, X. Medical image encryption scheme based on self-verification matrix. IET Image Process. 2021, 15, 2787–2798. [Google Scholar] [CrossRef]
- Adeyemi, V.A.; Nuñez-Perez, J.C.; Ibarra, Y.S.; Perez-Pinal, F.J.; Tlelo-Cuautle, E. FPGA Realization of the Parameter-Switching Method in the Chen Oscillator and Application in Image Transmission. Symmetry 2021, 13, 923. [Google Scholar] [CrossRef]
- Al-Hussein, A.B.A.; Tahir, F.R.; Al-Suhail, G.A. Design and FPGA Implementation of a Hyper-Chaotic System for Real-time Secure Image Transmission. Iraqi J. Electr. Electron. Eng. 2025, 21, 55–68. [Google Scholar] [CrossRef]
- Abdullah, H.A.; Abdullah, H.N. FPGA implementation of color image encryption using a new chaotic map. Indones. J. Electr. Eng. Comput. Sci. 2019, 13, 129. [Google Scholar] [CrossRef]
- Younas, I.; Khan, M. A New Efficient Digital Image Encryption Based on Inverse Left Almost Semi Group and Lorenz Chaotic System. Entropy 2018, 20, 913. [Google Scholar] [CrossRef]
- Ciylan, F.; Ciylan, B.; Atak, M. FPGA-Based Chaotic Image Encryption Using Systolic Arrays. Electronics 2023, 12, 2729. [Google Scholar] [CrossRef]
- Yu, F.; Liu, L.; He, B.; Huang, Y.; Shi, C.; Cai, S.; Song, Y.; Du, S.; Wan, Q. Analysis and FPGA Realization of a Novel 5D Hyperchaotic Four-Wing Memristive System, Active Control Synchronization, and Secure Communication Application. Complexity 2019, 2019, 4047957. [Google Scholar] [CrossRef]
- Peng, X.; Zeng, Y. Image encryption application in a system for compounding self-excited and hidden attractors. Chaos Solitons Fractals 2020, 139, 110044. [Google Scholar] [CrossRef]
- Yu, F.; Shen, H.; Zhang, Z.; Huang, Y.; Cai, S.; Du, S. A new multi-scroll Chua’s circuit with composite hyperbolic tangent-cubic nonlinearity: Complex dynamics, Hardware implementation and Image encryption application. Integration 2021, 81, 71–83. [Google Scholar] [CrossRef]



| Metric | LUT | FF | DSP | I/O | BUFG | LUTRAM |
|---|---|---|---|---|---|---|
| (134,600) | (269,200) | (740) | (400) | (32) | (46,200) | |
| Resource | 16,213 | 3252 | 528 | 75 | 12 | 234 |
| Utilization | 12.05% | 1.12% | 71.35% | 18.75% | 37.5% | 0.51% |
| Module | LUT (134,600) | FF (269,200) | DSP (740) | I/O (400) | BUFG (32) | LUTRAM (46,200) |
|---|---|---|---|---|---|---|
| Top level | 0 | 0 | 0 | 75 | 12 | 0 |
| 4D master | 2530 | 368 | 120 | 0 | 0 | 0 |
| 4D slave | 2394 | 368 | 122 | 0 | 0 | 0 |
| 5D master | 2938 | 452 | 142 | 0 | 0 | 0 |
| 5D slave | 2809 | 452 | 144 | 0 | 0 | 0 |
| Synchronizer | 427 | 389 | 0 | 0 | 0 | 0 |
| Permutation | 1595 | 187 | 0 | 0 | 0 | 20 |
| Forward diffusion | 229 | 198 | 0 | 0 | 0 | 19 |
| Backward diffusion | 211 | 118 | 0 | 0 | 0 | 35 |
| Bit flip and mask | 219 | 110 | 0 | 0 | 0 | 43 |
| Inverse permutation | 1592 | 186 | 0 | 0 | 0 | 20 |
| Inverse forward diffusion | 197 | 84 | 0 | 0 | 0 | 19 |
| Inverse backward diffusion | 117 | 84 | 0 | 0 | 0 | 35 |
| Inverse bit flip and mask | 110 | 84 | 0 | 0 | 0 | 43 |
| Encrypted Image | |||||
|---|---|---|---|---|---|
| R | G | B | Grayscale | ||
| R | 5.6357 | −0.0034 | −0.0032 | ||
| Original Image | G | −0.0049 | −0.0072 | −0.0057 | 9.2066 |
| B | 3.7362 | −4.8187 | −6.1081 | ||
| R | G | B | RGB | Grayscale | |
|---|---|---|---|---|---|
| Original Image | 7.8109 | 7.7828 | 7.1683 | 7.7963 | 7.5446 |
| Encrypted Image | 7.9965 | 7.9974 | 7.9971 | 7.9991 | 7.9972 |
| References | RGB Image | Greyscale Image | ||
|---|---|---|---|---|
| Red | Green | Blue | ||
| This work | 3.7362 | −4.8187 | −6.1081 | 9.2066 |
| [45] | 0.0001 | −0.0002 | 0.0003 | N/A |
| [59] | 0.0019 | −0.0025 | −0.0031 | N/A |
| [60] | 0.0008 | 0.0035 | −0.0059 | N/A |
| [61] | 0.0316 | 0.0498 | 0.0296 | 0.0352 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nuñez-Perez, J.-C.; Afolabi, O.-M.; Adeyemi, V.-A.; Sandoval-Ibarra, Y.; Tlelo-Cuautle, E. FPGA Implementation of Secure Image Transmission System Using 4D and 5D Fractional-Order Memristive Chaotic Oscillators. Fractal Fract. 2025, 9, 506. https://doi.org/10.3390/fractalfract9080506
Nuñez-Perez J-C, Afolabi O-M, Adeyemi V-A, Sandoval-Ibarra Y, Tlelo-Cuautle E. FPGA Implementation of Secure Image Transmission System Using 4D and 5D Fractional-Order Memristive Chaotic Oscillators. Fractal and Fractional. 2025; 9(8):506. https://doi.org/10.3390/fractalfract9080506
Chicago/Turabian StyleNuñez-Perez, Jose-Cruz, Opeyemi-Micheal Afolabi, Vincent-Ademola Adeyemi, Yuma Sandoval-Ibarra, and Esteban Tlelo-Cuautle. 2025. "FPGA Implementation of Secure Image Transmission System Using 4D and 5D Fractional-Order Memristive Chaotic Oscillators" Fractal and Fractional 9, no. 8: 506. https://doi.org/10.3390/fractalfract9080506
APA StyleNuñez-Perez, J.-C., Afolabi, O.-M., Adeyemi, V.-A., Sandoval-Ibarra, Y., & Tlelo-Cuautle, E. (2025). FPGA Implementation of Secure Image Transmission System Using 4D and 5D Fractional-Order Memristive Chaotic Oscillators. Fractal and Fractional, 9(8), 506. https://doi.org/10.3390/fractalfract9080506










