Abstract
In this study, we focus on solving the nonlinear time-fractional Hirota–Satsuma coupled Korteweg–de Vries (KdV) and modified Korteweg–de Vries (MKdV) equations, using the Yang transform iterative method (YTIM). This method combines the Yang transform with a new iterative scheme to construct reliable and efficient solutions. Readers can understand the procedures clearly, since the implementation of Yang transform directly transforms fractional derivative sections into algebraic terms in the given problems. The new iterative scheme is applied to generate series solutions for the provided problems. The fractional derivatives are considered in the Caputo sense. To validate the proposed approach, two numerical examples are analysed and compared with exact solutions, as well as with the results obtained from the fractional reduced differential transform method (FRDTM) and the q-homotopy analysis transform method (q-HATM). The comparisons, presented through both tables and graphical illustrations, confirm the enhanced accuracy and reliability of the proposed method. Moreover, the effect of varying the fractional order is explored, demonstrating convergence of the solution as the order approaches an integer value. Importantly, the time-fractional Hirota–Satsuma coupled KdV and modified Korteweg–de Vries (MKdV) equations investigated in this work are not only of theoretical and computational interest but also possess significant implications for achieving global sustainability goals. Specifically, these equations contribute to the Sustainable Development Goal (SDG) “Life Below Water” by offering advanced modelling capabilities for understanding wave propagation and ocean dynamics, thus supporting marine ecosystem research and management. It is also relevant to SDG “Climate Action” as it aids in the simulation of environmental phenomena crucial to climate change analysis and mitigation. Additionally, the development and application of innovative mathematical modelling techniques align with “Industry, Innovation, and Infrastructure” promoting advanced computational tools for use in ocean engineering, environmental monitoring, and other infrastructure-related domains. Therefore, the proposed method not only advances mathematical and numerical analysis but also fosters interdisciplinary contributions toward sustainable development.
1. Introduction
Recent research has shown that a variety of physical phenomena in engineering, physics, chemistry, and other scientific fields can be effectively represented using models and mathematical techniques from fractional calculus, namely, the concept of non-integer order derivatives and integrals. The applications of fractional order calculus in fractional order integration and differentiation make it an essential component of calculus. The idea of fractional calculus is not new. It is a variation of classical calculus that deals with ordinary differentiation and integration of arbitrary order. It basically started with a letter that Leibniz wrote to L’Hospital in the late seventeenth century. The basic idea behind fractional calculus is that natural events are modelled using fractional operators rather than integer operators. As a result, the main focus of fractional calculus is on properties that traditional theory cannot adequately describe [1,2,3,4]. The two main categories of fractional derivatives are Liouville–Caputo and Riemann–Liouville derivatives. Periodically, new definitions of integrals and fractional operators are presented. These are basically extensions to the Liouville–Caputo operator that provide new features that were not available before and are fundamental to the development of fractional calculus theory. As a result, fractional calculus has been shown to be a useful tool for studying topics associated to applied science. In recent years, fractional calculus has been applied extensively. Numerous linear and non-linear phenomena have been studied, using fractional calculus [5,6]. A few domains that employ fractional order modelling are education [7], agriculture [8], ocean waves [9], health [10], robotics [11], and construction [12].
In the applied sciences, including fluid mechanics, quantum mechanics, plasma physics, ocean engineering, and nonlinear optics, nonlinear fractional differential equations (NFDEs) provide an efficient description of a wide range of physical phenomena. Numerous studies in fields such as control theory, biology, economics, and electrodynamics have demonstrated that NFDEs play a vital role in modelling and understanding complex systems and dynamic behaviours observed in real-life applications. In recent years, these equations have garnered significant attention, due to their applicability in diverse scientific domains, notably in optical fibres, chemical physics, and solid-state physics. Obtaining accurate analytical or approximate solutions to such equations is essential for deepening our understanding of nonlinear processes in natural and engineered environments. Finding the solution to NFDEs might be complicated at times. The exact analytical solutions of many NFDEs are not known; hence, approximation and numerical methods must be employed to obtain the desired outcomes. Therefore, effective computational techniques may be needed to solve NFDEs. In recent years, a number of significant works on fractional calculus have been researched, and several books have been written by different writers, including Podlubny [13], Miller and Ross [14], Kilbas et al. [15], and Baleanu et al. [16,17]. These books provide a thorough analysis of fractional calculus, which could aid researchers in understanding the fundamental concepts of the subject. Consequently, a number of semi-analytical and numerical methods have been developed for the resolution of these kinds of physical model issues, including the homotopy perturbation method [18], the conformal decomposition method [19], the Adomian decomposition method [20,21], and the modified decomposition method [22]. Some other researches can be found in [23,24,25,26,27,28] relating to the complex study of fractional calculus and various methods.
The generalised time-fractional Hirota–Satsuma coupled KdV and MKdV equations with appropriate initial conditions are solved and explored in the current research. The most important nonlinear equations in physics and mathematics are the generalised Hirota–Satsuma coupled KdV and MKdv systems. The Toda lattice equation, a well-known soliton equation in one space and one time dimension, which is used to simulate the interaction of nearby particles of similar weight in a crystal lattice formation, is the general case of the Hirota–Satsuma coupled KdV equation. These models have numerous applications in numerous domains of nonlinear research. For strings and multi-strings, these systems can be employed to describe general properties of string dynamics in constant curvature space. The interaction of two long waves with distinct dispersion relationships is also explored by these equations. Furthermore, wave propagation is described by these models in the study of shallow-water waves.
The system of partial FDES of the following type represents the time-fractional Hirota–Satsuma coupled KdV:
and a time-fractional coupled mKdV system is
where ℓ is a constant and is a parameter describing the order of the time-fractional derivative of , ), and , respectively. Our target is to achieve solutions in the form of recurrence relations by applying the Yang transform iterative method (YTIM), the novel iterative methodology provided by Gejji and Jafari [29]. In 2006, Jafari and Daftardar-Gejji [29,30] presented a novel iterative technique for obtaining numerical solutions to nonlinear functional equations. The iterative method has been employed to address a large number of fractional boundary value problems [31] and nonlinear differential equations of both integer and fractional order [32]. In this method, we use Yang transform (YT) with the iterative approach. It is also advantageous to use this process to obtain an accurate approximation of the solution. We can say that the projected approach can reduce the time and work of the computation in comparison to the established schemes while preserving great efficiency in the approximate results; the size decreasing amounts to an enhancement of the execution of technique. The following is the paper’s order. We provide a few foundational definitions in Section 2. Section 3 provides a brief presentation of the Yang transform and an analysis of the new iterative technique. The convergence analysis of the suggested method is discussed in Section 4 of the manuscript. The time-fractional coupled KdV and mKdV systems’ approximate solutions, graphs, and tables are shown in Section 5 and Section 6. The conclusions are given in Section 7.
2. Basic Definitions
In this section, we offer some basic definitions related to our current research.
Definition 1.
The Caputo definition of a fractional derivative is given as [33,34]
Definition 2.
The Yang transform (YT) of the function is given as [35,36]
with inverse transformation as
Definition 3.
The YT of a non-integer derivative is given as [35,36]
Definition 4.
The YT of an nth derivative is given as [35,36]
3. Roadmap of the YTIM
In this section, we present a general description of the YTIM. We consider the general nonlinear FPDE of the form
with
where represents the Caputo derivative, and are linear and nonlinear terms, respectively, and is the source term.
By implementing YT to (8),
By using the YT differentiation property, we have
By implementing the inverse Yang transform, Equation (10) can be written as
By the iterative approach, we obtain
and the nonlinear term is decomposed as
By using Equations (12)–(14) into Equation (11), we obtain
In terms of an iterative formula, we obtain
At the end, the solution in series form to Equation (8) for the m-term illustrates
4. Convergence Analysis
Theorem 1.
The outcome of (19) is unique at
Proof.
Assume a Banach space ∀ continuous function on J with the norm Let H be a Banach space, and is a non-linear mapping, where
Suppose that and , where and are two separate function values and , are Lipschitz constants.
I is a contraction as . The outcome of (8) is unique, in terms of the Banach fixed point theorem. □
Theorem 2.
The outcome of (19) is convergent.
Proof.
Assume . To show that is a Cauchy sequence in H, consider
Let ; then,
where . Similarly, we have
As , we obtain . Hence,
Since when . Hence, is a Cauchy sequence in H, demonstrating that the series is convergent. □
5. Applications
5.1. Example
We consider the time-fractional Hirota–Satsuma coupled KdV [37],
with
where and are arbitrary constants.
5.2. Example
We consider the time-fractional coupled modified KdV [37],
with
where and are arbitrary constants.
6. Results and Discussion
Here, we report the results of our numerical simulations of the nonlinear time-fractional Hirota–Satsuma coupled KdV and MKdV equations using the proposed technique. We used 2D and 3D graphs and tables to show the behaviour of the obtained solution. Figure 1, Figure 2 and Figure 3 represent the 3D comparison plots of the exact and YTIM solutions of Example 5.1 for ,, and , while Figure 4, Figure 5 and Figure 6 represent the 3D solution graph at of Example 5.1 for ,, and . Similarly, Figure 7, Figure 8 and Figure 9 represent the 3D as well as the 2D solution graph at different fractional orders of Example 5.1. Also, Table 1, Table 2 and Table 3 show a comparison of the exact solution with the proposed method solution at different fractional orders of for , , and . We compare the solution of the third-order approximation with FRDTM in Table 4, Table 5 and Table 6. The comparison shows a high degree of agreement between the analytical and exact results. This suggests that the solutions generated by YTIM are more suitable than those obtained FRDTM. Thus, compared to FRDTM, the suggested strategy is a dependable, innovative method that needs less calculation time and is simpler and more adaptable. In the same manner, Figure 10 and Figure 11 represent the 3D comparison plots of the exact and YTIM solutions of Example 5.2 for and , while Figure 12 and Figure 13 represent the 3D solution graph at of Example 5.2 for and . Similarly, Figure 14 and Figure 15 represent the 3D and 2D solution graph at different fractional orders of Example 5.2. Also, we compared the absolute error of the third-order approximation with q-HATM in Table 7 and Table 8 for and . These error tables were essential for evaluating both methods’ accuracy and convergence. A smaller absolute error suggests a more accurate approximation, suggesting that our approach is capable of accurately simulating the behaviour of the associated nonlinear partial differential equations. The tabular and graphical representations have verified that fractional-order solutions converge to integer-order solutions. Our solution series quickly converges to the precise solution when we simply compute the iteration up to three terms. A few more iterations could be investigated, in order to improve the accuracy of the estimated results. We can simulate and visualise the physical characteristics of a non-linear problem with FC, which allows us to examine and evaluate its physical behaviour. The method that has been proposed is more effective and appropriate for examining complicated coupled fractional-order problems. By Maple 2015, all of the numerical computations have been performed.
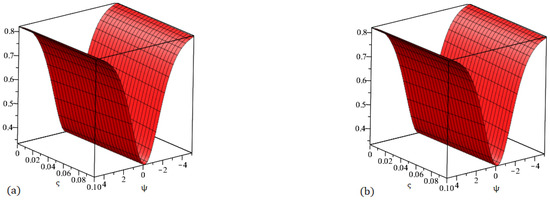
Figure 1.
Graph (a) demonstrating the accurate solution and (b) demonstrating our method solution for .

Figure 2.
Graph (a) demonstrating the accurate solution and (b) demonstrating our method solution for .
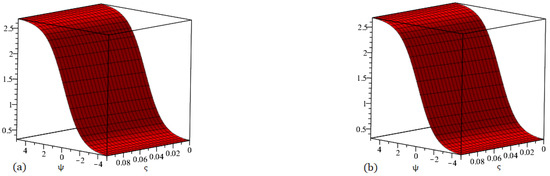
Figure 3.
Graph (a) demonstrating the accurate solution and (b) demonstrating our method solution for .
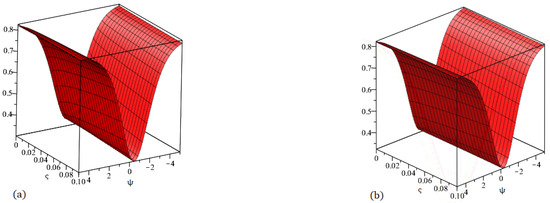
Figure 4.
Graphs demonstrating our method solution for at (a) and (b) .

Figure 5.
Graphs demonstrating our method solution for at (a) and (b) .
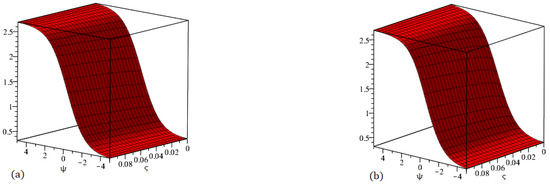
Figure 6.
Graphs demonstrating our method solution for at (a) and (b) .
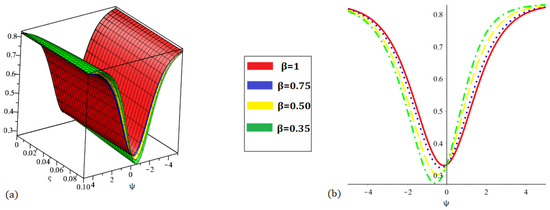
Figure 7.
Graph (a) demonstrating three-dimensional and (b) demonstrating two-dimensional nature of the proposed method result for at various fractional orders of .
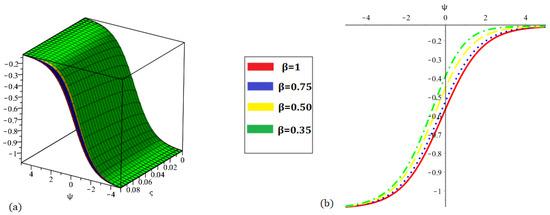
Figure 8.
Graph (a) demonstrating three-dimensional and (b) demonstrating two-dimensional nature of the proposed method result for at various fractional orders of .
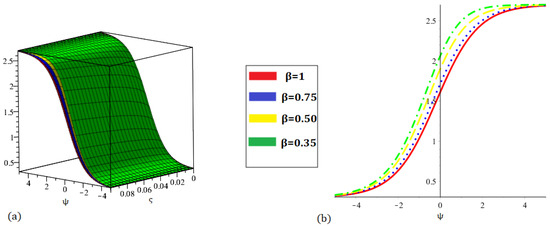
Figure 9.
Graph (a) demonstrating three-dimensional and (b) demonstrating two-dimensional nature of the proposed method result for at various fractional orders of .

Table 1.
Numerical comparison between accurate and proposed method solution at different fractional orders for .

Table 2.
Numerical comparison between accurate and proposed method solutions at different fractional orders for .

Table 3.
Numerical comparison between accurate and proposed method solutions at different fractional orders for .

Table 4.
Numerical comparison between proposed method solution with accurate solution and fractional reduced differential transform method (FRDTM) for .

Table 5.
Numerical comparison between proposed method solution with accurate solution and FRDTM for .

Table 6.
Numerical comparison between proposed method solution with accurate solution and FRDTM for .

Figure 10.
Graph (a) demonstrating the accurate solution and (b) demonstrating our method solution for .
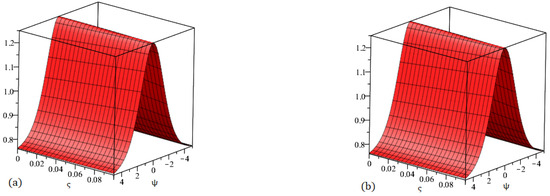
Figure 11.
Graph (a) demonstrating the accurate solution and (b) demonstrating our method solution for .
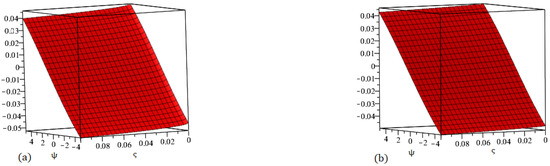
Figure 12.
Graphs demonstrating our method solution for at (a) and (b) .
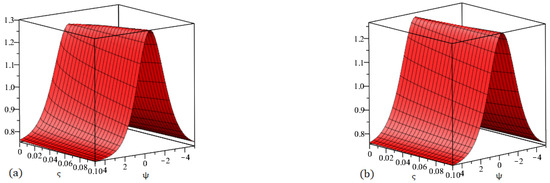
Figure 13.
Graphs demonstrating our method solution for at (a) and (b) .
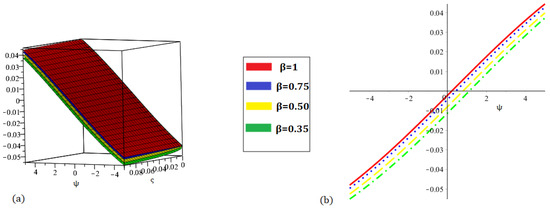
Figure 14.
Graph (a) demonstrating three-dimensional and (b) demonstrating two-dimensional nature of the proposed method result for at various fractional orders of .
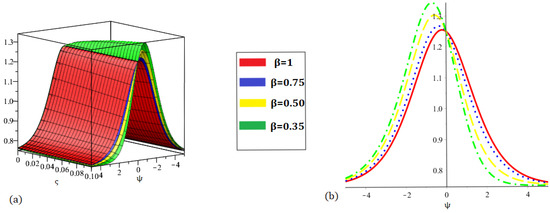
Figure 15.
Graph (a) demonstrating three-dimensional and (b) demonstrating two-dimensional nature of the proposed method result for at various fractional orders of .

Table 7.
Numerical comparison between proposed method solution and q-homotopy analysis transform method (q-HATM) for .

Table 8.
Numerical comparison between proposed method solution and q-homotopy analysis transform method (q-HATM) for .
7. Conclusions
In this research, we used a coupling technique that combines the new iterative method and the Yang transform to achieve approximate solutions to a coupled mKdV system and a time-fractional generalised Hirota–Satsuma coupled KdV system. When the outcomes of this approach are compared to the precise solution, it becomes clear that the suggested approach is remarkably straightforward and allows for dealing with the nonlinear terms easily. The suggested approach solution exhibits strong agreement with the exact solution when two nonlinear systems are solved. It has been verified that the suggested approach, which demonstrates quick convergence, requires considerably lower computational effort. When the approximate and exact solutions are compared, it is found that the approximate series solutions for the first few terms are extremely accurate and converge quickly to the solutions of the actual physical problems. The findings demonstrate that the current method is very precise, trustworthy, and best suited for computer algorithms. It is also a useful mathematical tool for many researchers studying linear or nonlinear fractional differential equations in the applied sciences and engineering fields. In addition, the current method can be used in combination with a number of other numerical techniques to obtain an approximate and analytical solution for fractional differential equations.
Author Contributions
Conceptualization, M.M.A.; Methodology, M.M.A. and R.A.; Software, M.M.A. and R.A.; Validation, M.M.A.; Formal analysis, M.M.A. and R.A.; Project administration, M.M.A.; Funding acquisition, M.M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by Prince Sattam bin Abdulaziz University under project number (PSAU/2025/R/1446).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Mainardi, F.; Raberto, M.; Gorenflo, R.; Scalas, E. Fractional calculus and continuous-time finance II: The waiting-time distribution. Phys. A Stat. Mech. Its Appl. 2000, 287, 468–481. [Google Scholar] [CrossRef]
- He, J.H. Some applications of nonlinear fractional differential equations and their approximations. Bull. Sci. Technol. 1999, 15, 86–90. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus. In Integrations and Differentiations of Arbitrary Order; Descartes Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Saad, K.M. Comparative study on fractional isothermal chemical model. Alex. Eng. J. 2021, 60, 3265–3274. [Google Scholar] [CrossRef]
- Ahmad, H.; Alam, N.; Omri, M. New computational results for a prototype of an excitable system. Results Phys. 2021, 28, 104666. [Google Scholar] [CrossRef]
- Qayyum, M.; Ahmad, E.; Afzal, S.; Sajid, T.; Jamshed, W.; Musa, A.; Tag El Din, E.S.M.; Iqbal, A. Fractional analysis of unsteady squeezing flow of casson fluid via homotopy perturbation method. Sci. Rep. 2022, 12, 18406. [Google Scholar] [CrossRef]
- Yusuf, A.; Qureshi, S.; Mustapha, U.T.; Musa, S.S.; Sulaiman, T.A. Fractional modeling for improving scholastic performance of students with optimal control. Int. J. Appl. Comput. Math. 2022, 8, 37. [Google Scholar] [CrossRef]
- Nisar, K.S.; Logeswari, K.; Vijayaraj, V.; Baskonus, H.M.; Ravichandran, C. Fractional order modeling the gemini virus in capsicum annuum with optimal control. Fractal Fract. 2022, 6, 61. [Google Scholar] [CrossRef]
- Qayyum, M.; Ahmad, E.; Saeed, S.T.; Ahmad, H.; Askar, S. Homotopy perturbation methodbased soliton solutions of the time-fractional (2+1)-dimensional wu-zhang system describing long dispersive gravity water waves in the ocean. Front. Phys. 2023, 11, 1178154. [Google Scholar] [CrossRef]
- Hassani, H.; Machado, J.A.T.; Avazzadeh, Z.; Naraghirad, E.; Mehrabi, S. Optimal solution of the fractional-order smoking model and its public health implications. Nonlinear Dyn. 2022, 108, 2815–2831. [Google Scholar] [CrossRef]
- Batiha, I.M.; Njadat, S.A.; Batyha, R.M.; Zraiqat, A.; Dababneh, A.; Momani, S. Design fractionalorder PID controllers for single-joint robot arm model. Int. J. Adv. Soft Comput. Appl. 2022, 14, 97–114. [Google Scholar]
- Wang, C.; Zhou, X.; Shi, X.; Jin, Y. Variable fractional order sliding mode control for seismic vibration suppression of uncertain building structure. J. Vib. Eng. Tech. 2021, 10, 299–312. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Miller, S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley and Sons: New York, NY, USA, 1993. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier Science B.V.: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific Publishing Company: Boston, MA, USA, 2012. [Google Scholar]
- Baleanu, D.; Machado, J.A.T.; Luo, A.C. Fractional Dynamics and Control; Springer: New York, NY, USA, 2012. [Google Scholar]
- Wu, Y.; He, J.H. Homotopy perturbation method for nonlinear oscillators with coordinate dependent mass. Results Phys. 2018, 10, 270–271. [Google Scholar] [CrossRef]
- Edeki, S.O.; Akinlabi, G.O.; Jena, R.M.; Ogundile, O.P.; Chakravertys, S. Conformable decomposition method for timespace fractional intermediate scalar transportation model. J. Theor. Appl. Inf. Technol. 2019, 97, 4251–4258. [Google Scholar]
- Momani, S.; Odibat, Z. Analytical solution of a time-fractional Navier-Stokes equation by Adomian decomposition method. Appl Math Comput. 2006, 177, 488–494. [Google Scholar] [CrossRef]
- Yavuz, M.; Ozdemir, N. A quantitative approach to fractional option pricing problems with decomposition series. Konuralp J. Math. 2018, 6, 102–109. [Google Scholar]
- Edeki, S.O.; Motsepa, T.; Khalique, C.M.; Akinlabi, G.O. The Greek parameters of a continuous arithmetic Asian option pricing model via Laplace Adomian decomposition method. Open Phys. 2018, 16, 780–785. [Google Scholar] [CrossRef]
- Hemeda, A.A. Homotopy perturbation method for solving partial differential equations of fractional order. J. Math. Anal. 2012, 6, 2431–2448. [Google Scholar]
- Sakar, M.G.; Erdogan, F.; Yildirim, A. Variational iteration method for the time-fractional Fornberg-Whitham equation. Comput. Math. Appl. 2012, 63, 1382–1388. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, S. Residual power series method for fractional Burger types equations. Nonlinear Eng. 2016, 5, 235–244. [Google Scholar] [CrossRef]
- Yokus, A.; Yavuz, M. Novel comparison of numerical and analytical methods for fractional burger-fisher equation. Discret. Contin. Dyn. Syst.-Ser. S 2021, 14, 2591–2606. [Google Scholar] [CrossRef]
- AlBaidani, M.M. Comparative Study of the Nonlinear Fractional Generalized Burger-Fisher Equations Using the Homotopy Perturbation Transform Method and New Iterative Transform Method. Fractal Fract. 2025, 9, 390. [Google Scholar] [CrossRef]
- Cattani, C. Harmonic wavelet solutions of the Schrodinger equation. Int. J. Fluid Mech. Res. 2003, 30, 463–472. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Jafari, H. An iterative method for solving nonlinear functional equations. J. Math. Anal. Appl. 2006, 316, 753–763. [Google Scholar] [CrossRef]
- Jafari, H. Iterative Methods for Solving System of Fractional Differential Equations. Doctoral Dissertation, Pune University, Pune, India, 2006. [Google Scholar]
- Daftardar-Gejji, V.; Bhalekar, S. Solving fractional boundary value problems with Dirichlet boundary conditions using a new iterative method. Comput. Math. Appl. 2010, 59, 1801–1809. [Google Scholar] [CrossRef]
- Bhalekar, S.; Daftardar-Gejji, V. Solving evolution equations using a new iterative method. Numer. Methods Part. Differ. Equ. Int. J. 2010, 26, 906–916. [Google Scholar] [CrossRef]
- Liu, H.; Khan, H.; Mustafa, S.; Mou, L.; Baleanu, D. Fractional-order investigation of diffusion equations via analytical approach. Front. Phys. 2021, 8, 568554. [Google Scholar] [CrossRef]
- AlBaidani, M.M. Analytical Insight into Some Fractional Nonlinear Dynamical Systems Involving the Caputo Fractional Derivative Operator. Fractal Fract. 2025, 9, 320. [Google Scholar] [CrossRef]
- Dattu, M.K.U. New integral transform: Fundamental properties, investigations and applications. IAETSD J. Adv. Res. Appl. Sci. 2018, 5, 534–539. [Google Scholar]
- Ganie, A.H.; Khan, A.; Alhamzi, G.; Saeed, A.M. A new solution of the nonlinear fractional logistic differential equations utilizing efficient techniques. AIP Adv. 2024, 14, 035134. [Google Scholar] [CrossRef]
- Fan, E. Soliton solutions for a generalized Hirota-Satsuma coupled KdV equation and a coupled MKdV equation. Phys. Lett. A 2001, 282, 18–22. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).