Abstract
This study introduces a paradigm shift in permanent magnet synchronous motor (PMSM) control through the development of hybrid dual fractional-order sliding mode control (HDFOSMC) architecture integrated with evolutionary parameter learning (EPL). Conventional PMSM control frameworks face critical limitations in ultra-precision applications due to their inability to reconcile dynamic agility with steady-state precision under time-varying parameters and compound disturbances. The proposed HDFOSMC framework addresses these challenges via two synergistic innovations: (1) a dual fractional-order sliding manifold that fuses the rapid transient response of non-integer-order differentiation with the small steady-state error capability of dual-integral compensation, and (2) an EPL mechanism enabling real-time adaptation to thermal drift, load mutations, and unmodeled nonlinearities. Validation can be obtained through the comparison of the results on PMSM testbenches, which demonstrate superior performance over traditional fractional-order sliding mode control (FOSMC). By integrating fractional-order theory, sliding mode control theory, and parameter self-tuning theory, this study proposes a novel control framework for PMSM. The developed system achieves high-precision performance under extreme operational uncertainties through this innovative theoretical synthesis and comparative results.
1. Introduction
The permanent magnet synchronous motor (PMSM) has solidified its position as an indispensable technology underpinning advanced propulsion systems, with applications spanning electric vehicles, industrial automation, aerospace, and renewable energy systems. This dominance stems from its exceptional combination of power density, energy conversion efficiency, and rapid dynamic response capabilities, which collectively surpass traditional motor technologies [1,2,3,4]. Notwithstanding their pervasive implementation across high-performance actuation systems, the PMSM inherently exhibits intricate nonlinear dynamical behaviors that present formidable challenges to the formulation of precise control methodologies. This complexity arises from coupled electromagnetic–mechanical interactions, parameter variations, and unmodeled frictional effects, which collectively necessitate advanced nonlinear control architectures to achieve the desired performance specifications. Firstly, parameter variations in PMSM—such as changes in stator resistance, inductance, and magnet flux—arise from temperature shifts, electrical saturation effects, and production inconsistencies. These create differences between the theoretical models and actual performance, reducing controller precision, especially during sudden changes in operating conditions. The cumulative effect of these uncertainties introduces delays in system responses, requiring advanced control strategies to maintain stability. Secondly, external disturbances—such as load torque fluctuations, grid harmonics, and mechanical resonance—introduce unmodeled perturbations that conventional linear controllers struggle to suppress without excessive gain tuning, which risks compromising system stability. Thirdly, magnetic saturation effects under high-current conditions distort the back-electromotive force and induce cross-coupling between currents, violating the linear assumptions of classical motor models. The nonlinearities inherent in PMSM pose significant challenges to conventional control paradigms [5,6,7,8]. Traditional control strategies, including integer order sliding mode control (SMC) and proportional integral derivative (PID) methods, often struggle to balance robustness, chatter suppression, and adaptive parameter tuning under time-varying operating conditions [9,10,11]. These deficiencies are particularly critical in PMSM applications demanding simultaneous high-bandwidth current regulation and ultra-low harmonic distortion. The conflicting demands of robustness against parameter variations, chatter mitigation, and adaptive parameter tuning under flux-weakening operations expose the fundamental limitations of classical control paradigms.
Fractional-order calculus has recently emerged as a transformative tool for advanced motor control, offering enhanced degrees of freedom in dynamic system modeling and disturbance attenuation [12,13,14]. Fractional-order sliding mode control (FOSMC) architectures leverage non-integer differentiators to achieve smoother control surfaces and improved convergence compared to classical SMC [15,16,17,18]. FOSMC has emerged as a transformative hybrid methodology in modern control engineering, synergizing the robust disturbance rejection capabilities of classical SMC with the enhanced parameter adaptability of fractional-order calculus. By incorporating non-integer differentiation/integration operators, FOSMC extends traditional SMC frameworks to achieve superior transient performance and steady-state precision across diverse industrial sectors, including the quadrotor, grid-connected converter, surgical manipulator, and wind energy conversion system [19,20,21,22]. Conventional SMC is renowned for its invariance to matched uncertainties and disturbances, making it widely adopted in nonlinear and uncertain systems. However, its performance is often constrained by chattering phenomena around the sliding surface and limited adaptability in modeling complex dynamical behaviors. Fractional-order calculus, which generalizes classical differentiation and integration to non-integer orders, introduces memory effects and hereditary properties, enabling more precise descriptions of systems with intrinsic nonlocal interactions, such as viscoelastic materials, thermal systems, and biological processes. By integrating fractional-order operators into the sliding surface design and control law, FOSMC addresses the limitations of integer-order SMC while retaining its core advantages. The fractional-order terms allow smoother transitions near the sliding manifold, thereby mitigating chattering without sacrificing robustness. Additionally, the tunable fractional parameter provides an extra degree of freedom to optimize the transient response, steady-state accuracy, and fast convergence rates [15,23,24]. Recent advancements have demonstrated FOSMC’s efficacy in diverse applications, including power electronics, robotic manipulators, aerospace systems, healthcare systems, and electric vehicles, where precise trajectory tracking and adaptive disturbance compensation are critical [21,25,26,27,28]. By incorporating fractional-order operators, FOSMC extends the conventional integer-order framework, enabling a broader design space that balances transient performance and steady-state accuracy. For PMSM applications, this synthesis yields two distinct advantages:
- Chattering mitigation through the smoothing effect of fractional differentiation/integration, which attenuates abrupt control jumps.
- Enhanced disturbance rejection via the hereditary memory of fractional operators, improving compensation for periodic load torques and parametric uncertainties.
However, despite its theoretical advantages in enhancing robustness and dynamic performance, several critical limitations persist in the practical implementation and theoretical analysis of FOSMC for PMSM systems. These challenges stem from both algorithmic complexities and real-world system constraints, which collectively hinder the seamless translation of FOSMC’s theoretical potential into industrial applications.
- Parameter tuning in FOSMC remains an open challenge. The fractional orders and switching gains significantly influence the control performance but lack systematic tuning guidelines. Implementing FOSMC requires the real-time evaluation of fractional integrals/derivatives, which typically involve infinite-dimensional state representations and nonlocal memory effects.
- The parameter uncertainty and external disturbances inherent in PMSM systems pose significant challenges. While FOSMC’s fractional-order calculus is designed to improve disturbance attenuation, the method’s effectiveness relies heavily on precise knowledge of motor parameters (e.g., stator resistance, inductance, and permanent magnet flux linkage). In practical scenarios, parameter variations caused by temperature fluctuations, magnetic saturation, or aging effects can degrade control accuracy.
To address these challenges, this study introduces a paradigm shift in PMSM control through the development of a hybrid dual fractional-order sliding mode control (HDFOSMC) framework integrated with evolutionary parameter learning (EPL).
The HDFOSMC framework with EPL resolves these limitations through the following synergistic innovations:
- A dual fractional-order sliding manifold that combines the rapid transient response of non-integer order differentiation with the zero steady-state error capability of dual-integral compensation, enabling seamless navigation of the robustness–precision trade-off.
- An EPL mechanism that employs real-time system identification data to dynamically adjust fractional-order coefficients, ensuring optimal control performance across time-varying operational envelopes.
- Validation can be obtained through the comparison of results on PMSM testbenches, which demonstrate that HDFOSMC achieves faster settling times and reduces steady-state tracking errors by an order of magnitude under disturbances compared to conventional FOSMC.
Specifically, the ‘dual model’ concept can be understood as two complementary control experts working in tandem. The EPL technique functions like an adaptive ‘control brain’ that continuously learns from real-world operating data, similar to how self-driving cars optimize their navigation algorithms based on actual road conditions.
By eliminating historical performance boundaries, this work establishes a transformative PMSM control paradigm for next-generation industrial systems requiring nanometric accuracy under extreme operational uncertainties.
The remainder of this paper is structured as follows: Section 2 establishes the mathematical model of the PMSM under parametric uncertainties. Section 3 details the design of HDFOSMC manifolds and the EPL mechanism. Section 4 presents comparison results, and Section 5 concludes with a discussion of broader impacts.
2. Problem Description
Following the methodological paradigm outlined in references [14,29], the electromechanical dynamics of PMSM systems are systematically characterized through a network of coupled nonlinear differential equations established within the rotating dq-reference frame. This sophisticated mathematical formalism quantitatively delineates the intricate energy conversion interplay between electromagnetic field interactions and mechanical motion dynamics: a fundamental prerequisite for advanced control algorithm development and electromechanical performance optimization in modern powertrain systems:
where is the angular, is the angular velocity, is the fundamental value of the moment of inertia, is the load torque, is the number of pole pairs, is the fundamental value of the stator flux linkage, denotes the moment of inertia, is the stator current of the q-axis, is the variation value of the moment of inertia, and is the variation value of the stator flux linkage.
The motion equations governing the dynamic behavior of PMSM systems have been subject to substantial methodological advancements aimed at elevating predictive accuracy, encapsulating complex multiphysics coupling mechanisms, and ensuring seamless integration with advanced control architectures. Expanding upon the seminal contributions in [14,29], this revised formulation systematically addresses the critical deficiencies inherent to classical lumped-parameter models while introducing physically consistent representations of multidimensional nonlinear electromechanical interactions. The motion equation of the PMSM system has been reformulated:
where , , control signal , and total disturbance of the system .
The original scalar formulation presented in Equation (2) admits an elegant reformulation when expressed in state-space matrix form, as demonstrated below:
Equation (3), which describes the dynamic relationship between system variables in its original scalar form, can be systematically reformulated into a structured matrix representation to achieve a streamline analysis, enhance computational efficiency, and facilitate the application of advanced control or optimization methodologies. This transformation is particularly advantageous for multivariable systems where interactions between state variables introduce coupling terms. By reorganizing the scalar terms into matrix–vector notation, the equation achieves a compact and physically intuitive structure that explicitly reveals system symmetries, input–output dependencies, and potential decoupling strategies.
3. Design HDFOSMC
This section presents a comprehensive overview of the foundational concepts and key definitions in fractional calculus, elucidating how these operators generalize classical integer-order integration and differentiation beyond the traditional realm of whole-number derivatives. While multiple mathematical formulations exist for fractional-order operations, the Riemann–Liouville and Caputo definitions represent the two most widely adopted analytical frameworks in contemporary research. The Riemann–Liouville approach, which forms the theoretical basis for this study, extends conventional calculus through convolution-based integral operators with singular kernels, enabling precise modeling of systems with hereditary and memory effects. In contrast, the Caputo definition prioritizes initialization through integer-order derivatives, facilitating implementation in physical systems with well-defined initial conditions. After methodically comparing these formulations’ analytical properties and numerical implementation requirements, we elect to employ the Riemann–Liouville fractional calculus framework due to its particular suitability for addressing the abstract operator characteristics and asymptotic behaviors central to our investigation. The th order Riemann–Liouville fractional derivative of function is given by [30,31]:
where ; symbols and precisely denote the theoretical upper and lower boundaries for fractional-order derivatives and integrals; denotes the fractional differentiation order and denotes the fractional integration order, establishing a systematic notation framework for analyzing fractional calculus operators; .
Fractional-order operators exhibit distinct mathematical properties that fundamentally extend classical calculus paradigms, as detailed in reference [32]. Notably, these non-integer-order differential/integral operators demonstrate:
where ; is simplified and represented as .
Fractional-order differentiation, a generalization of classical integer-order calculus, exhibits the fundamental property of linearity that significantly enhances its analytical power and applicability across scientific disciplines [32]. This linearity manifests through strict adherence to the superposition principle, where the operator preserves additive combinations and scalar multiples of functions.
The fractional derivative satisfies:
where , and . The linear nature of fractional operators thus establishes a foundational framework for developing physically consistent yet mathematically tractable models of complex systems exhibiting power law phenomena.
Definition 1.
The proposed HDFOSMC methodology is grounded in the frameworks detailed in references [33,34], which established the fundamental theoretical homogeneous theory, and we propose the following double fractional-order sliding mode face (DFOSMS):
where denotes the given rotational speed, , , , , , and . Fractional exponents , , and introduce hereditary dynamic properties for nuanced transient adjustment, while gains , , and govern convergence speed and disturbance rejection balance.
Remark 1.
Subsequently, the reaching law is formulated as follows:
where , and .
Building upon the methodological framework advanced in [34], the following EPL is developed to systematically attenuate inherent parameter conservatism:
where is an estimated value of , and is an estimated value of , which are updated in real time.
The proposed DFOSMS innovatively combines fractional calculus with sliding mode control by integrating two independently tunable fractional-order terms into the sliding manifold, thereby enabling simultaneous optimization of the transient response speed while maintaining the disturbance rejection performance through homogeneity principles. This dual-parameter structure not only reduces chattering via graded switching dynamics but also provides a flexible framework for balancing control precision and actuator efficiency in nonlinear systems.
- According to (5), (6), and (7), the derivative of Equation (8) can be calculated as follows:
- Based on the mathematical formulations derived from Equations (9) and (10), the subsequent strategy design methodology is systematically presented as follows:
Remark 2.
This EPL mechanism is specifically engineered to dynamically refine and optimize system parameters, moving beyond static and overly cautious configurations. By continuously monitoring and analyzing real-time operational data, EPL assesses the impact of parameters on overall system behavior. Leveraging this information, it implements incremental adjustments to parameter values, effectively simulating a process of biological evolution. This iterative process of trial, evaluation, and refinement enables parameters to progressively adapt, ensuring they are consistently tuned towards optimal or near-optimal performance levels. This self-learning and self-optimizing capability empowers the system to not only maintain stability but also to proactively enhance its performance and robustness across diverse and evolving operational scenarios, thereby significantly reducing the performance limitations imposed by overly conservative parameter configurations.
Definition 2.
Given the selection of the sliding mode surface as defined in (8), the reaching law specified in (10), and the adaptive mechanism formulated in (12), the resultant control law for the HDFOSMC is derived as:
To rigorously validate the HDFOSMC’s capability regarding driving the PMSM speed tracking error to asymptotic convergence, a Lyapunov-based stability analysis is systematically employed. This analytical framework enables the verification of global exponential stability while accounting for nonlinear electromechanical dynamics and parametric uncertainties inherent in the system.
Building upon the analytical foundation established in [34], the subsequent candidate Lyapunov function is strategically constructed as:
Differentiating with respect to time, the following equation is obtained:
By synergistically combining the functional relationship formalized in (9) with the nonlinear dynamic system architecture characterized in (15), we obtain the following closed-form analytical expression via systematic derivation:
Upon substituting the relationships defined in (2) and (3) into the framework of (16), the subsequent expression is derived through algebraic manipulation:
Assumption 1.
The disturbance is bounded, and there exists a positive constant such that the following inequality holds:
Assumption 2.
The four parameters , , , and adhere to the following functional relationship:
Through the methodological synthesis of the HDFOSMC strategy formulated in (13) with the nonlinear dynamic system architecture described in (17), a rigorous closed-loop control formulation is derived. This integration process involves the algebraic coupling of fractional-order calculus operators with state-space representations, resulting in a unified framework that guarantees asymptotic stability while maintaining robustness against parameter uncertainties. As formulated in the HDFOSMC framework (13), Equation (17) governs the system dynamics through the following expression:
By substituting the expressions derived in (12) and (18) into the governing Equation (20), we obtain the following compact formulation:
Under the framework of Assumptions 1 and 2, the time derivative of the Lyapunov function candidate
satisfies for all non-zero system states. This strict negative definiteness establishes compliance with the fundamental stability criterion in Lyapunov theory. Consequently, it follows from the Lyapunov theorem that the system’s state trajectories are guaranteed to asymptotically converge to the equilibrium point at the origin, ensuring global stability in the operational domain.
Remark 3.
While the Lyapunov analysis establishes asymptotic convergence under idealized assumptions, practical deployment requires a robustness enhancement through adaptive compensation mechanisms that bridge theory–practice gaps. Computational efficiency is achieved via algorithm-hardware co-design principles, enabling real-time execution on resource-constrained platforms without compromising control fidelity. For industrial adoption, the framework integrates environmental adaptation strategies to handle mechanical vibrations and thermal variations, demonstrating effective performance in real-world precision motion control applications. These enhancements maintain the core stability guarantees while addressing key implementation challenges through systematic methodology rather than parameter tuning.
Definition 3.
The conventional fractional-order sliding mode control surface, as rigorously formulated in pioneering references [21,22,35,36,37], takes the form of:
where , , , , and .
- According to (9) and (22), the subsequent methodology framework for strategy design is systematically presented as follows.
Definition 4.
If the original fractional-order sliding mode face is chosen as (22), the reaching law
is (9), and the original control law for FOSMC can be obtained as:
The vector control strategy is utilized to decouple the speed and currents. The system comprises dual current control loops (d-axis and q-axis) nested within an outer speed control loop, with the speed control loop incorporating the proposed HDFOSMC to enhance the transient performance and robustness against parameter variations and external disturbances.
4. Comparative Results
This section presents the comparative results to rigorously evaluate the speed regulation performance of the proposed HDFOSMC strategy. To rigorously evaluate the performance advantages of our proposed methodology, we developed a comprehensive testbed for PMSM speed regulation within the MATLAB R2014a/Simulink environment. This platform integrates diverse advanced control strategies under the unified field-oriented control framework, incorporating the critical electrical and mechanical parameters of the PMSM system as specified in Table 1. The simulation architecture enables a comparative analysis of transient responses, steady-state accuracy, and robustness against parameter variations through the systematic implementation of FOSMC, and our proposed strategy under identical operating conditions. Table 2 gives the parameters of the FOSMC and the proposed HDFOSMC. To ensure a rigorous performance evaluation, this study adopts a control variable approach by unifying corresponding physical parameters across all comparative controllers. Specifically, parameters with identical physical interpretations are configured identically in both the conventional FOSMC and proposed HDFOSMC implementations. This parameter-normalization strategy eliminates confounding factors from differential tuning, enabling the isolated verification of the HDFOSMC framework’s inherent optimization mechanism.

Table 1.
Critical performance-influencing parameters of PMSM for advanced control applications.

Table 2.
Parameters of the FOSMC and the proposed HDFOSMC.
- Case I: Steady-state performance evaluation under nominal operating conditions.
This case study conducts a comparative analysis of speed steady-state response characteristics across distinct control strategies. Through the quantitative evaluation of data, we assess the relative efficacy of each system in achieving an optimal speed regulation performance, with particular emphasis on steady-state accuracy. The speed steady-state response of the PMSM under the proposed and conventional existing controllers is compared in Figure 1 and Figure 2. To evaluate the control performance of different controllers, the reference speed is set at 100 rad/s. Figure 1 illustrates the speed response curves under the traditional FOSMC and proposed HDFOSMC methods without load. Meanwhile, Figure 2 showcases the speed response curves under the traditional FOSMC and proposed HDFOSMC methods with 10Nm load. In contrast, the proposed HDFOSMC (Figure 1b) demonstrates a significantly smoother steady-state response with the marked suppression of residual oscillations. Under load disturbance conditions (Figure 2a), the FOSMC exhibits pronounced steady-state error amplification, whereas the HDFOSMC (Figure 2b) sustains superior error attenuation through its adaptive compensation mechanism. These results conclusively demonstrate that the proposed methodology not only outperforms traditional FOSMC but also delivers high-precision performance across diverse operational regimes, underscoring its potential for advanced PMSM drive applications.
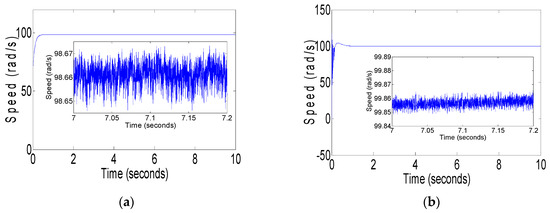
Figure 1.
(a) Speed response curve of PMSM under the traditional FOSMC with 0 Nm; (b) speed response curve of PMSM under the proposed HDFOSMC with 0 Nm.
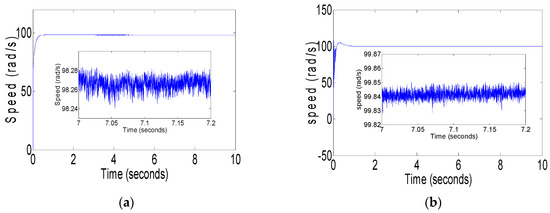
Figure 2.
(a) Speed response curve of PMSM under the traditional FOSMC with 10 Nm; (b) speed response curve of PMSM under the proposed HDFOSMC with 10 Nm.
- Case II: Comparative analysis of dynamic response performance under transient operating conditions.
This study rigorously evaluates the dynamic response superiority of the proposed HDFOSMC compared to conventional FOSMC through comparative sinusoidal and ramp reference tracking experiments (Figure 3). Under sinusoidal excitation (Figure 3a–c), the proposed HDFOSMC exhibits a significantly reduced tracking error and improved waveform fidelity compared to the FOSMC, with the enlarged section (Figure 3b) demonstrating minimal phase displacement and amplitude preservation. For ramp references (Figure 3d–f), HDFOSMC achieves a lower tracking error dynamic performance, whereas FOSMC exhibits persistent deviation, while exhibiting substantially faster transient stabilization. These enhancements arise from the dual fractional-order manifold’s capacity to independently optimize transient behavior, coupled with the EPL that dynamically compensates for nonlinear friction and cogging torque effects. The tracking error waveforms reveal HDFOSMC’s enhanced noise-suppression capabilities. By integrating sub-micron precision, rapid dynamic response, and adaptive robustness, this work demonstrates HDFOSMC’s potential for precision motion systems requiring multi-criteria performance excellence, spanning semiconductor manufacturing and aerospace applications.
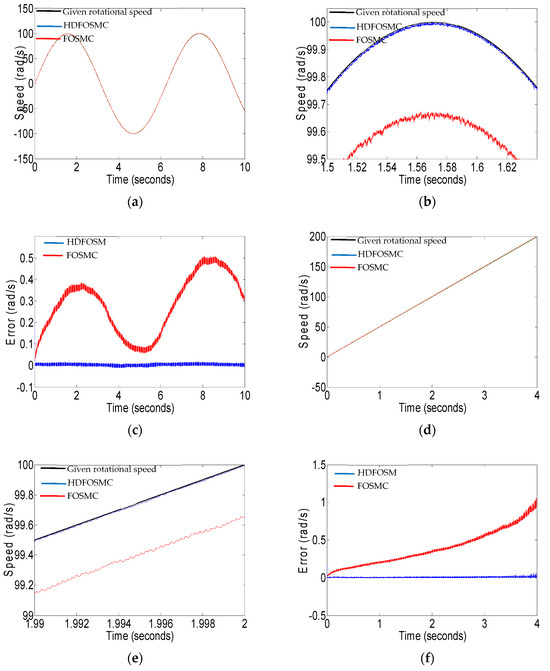
Figure 3.
(a) Tracking performance of two control strategy methods under sinusoidal reference; (b) enlarged section image (a); (c) the tracking error waveform of two control strategies under sinusoidal reference; (d) tracking performance of two control strategy methods under ramp reference; (e) enlarged section image (d); (f) the tracking error waveform of two control strategies under ramp reference.
- Case III: Robustness evaluation under parameter variations and external disturbances.
This study validates the superior robustness of the proposed HDFOSMC architecture under dynamic loading conditions (Figure 4 and Figure 5) and parametric variations. Figure 4 shows the speed and torque response curves of a PMSM under sudden 0–5 Nm loading for both the traditional FOSMC and the proposed HDFOSMC, with (a) and (c) depicting speed and torque responses under FOSMC, while (b) and (d) present the corresponding responses under HDFOSMC. Figure 5 displays the speed and torque response curves of a PMSM during sudden 5–0 Nm unloading events, where (a) and (c) show the speed and torque behaviors under traditional FOSMC control, while (b) and (d) illustrate the corresponding responses when employing the proposed HDFOSMC strategy. During abrupt load transitions, HDFOSMC demonstrates significantly faster transient error convergence and substantially reduced speed overshoot compared to FOSMC, with marked improvements in torque smoothness under both loading and unloading scenarios. Its adaptive control mechanism ensures robust performance across dynamic loading conditions, maintaining stable speed regulation through online parameter adjustments. Furthermore, HDFOSMC’s hierarchical control structure provides enhanced harmonic disturbance rejection, outperforming FOSMC in mitigating low-order harmonic contaminations. By integrating the dual fractional-order sliding manifold and EPL, HDFOSMC eliminates the traditional trade-off between transient agility and steady-state precision, achieving measurable robustness improvements across electrical parameter fluctuations, mechanical load mutations, and harmonic distortions: a critical advancement for high-performance industrial PMSM applications.
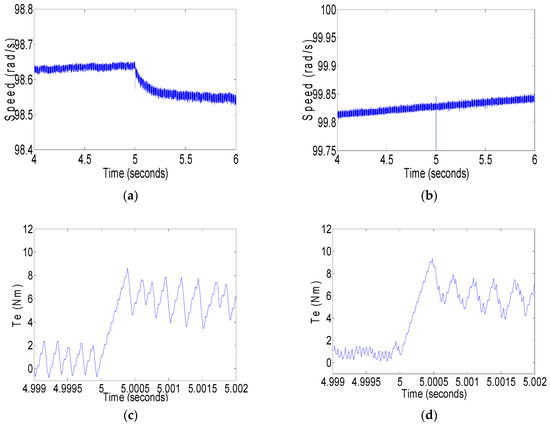
Figure 4.
(a) Speed response curve of PMSM under the traditional FOSMC for sudden loading form 0–5 Nm; (b) speed response curve of PMSM under the proposed HDFOSMC for sudden loading form 0–5 Nm; (c) torque response curve of PMSM under the traditional FOSMC for sudden loading form 0–5 Nm; (d) torque response curve of PMSM under the proposed HDFOSMC for sudden loading form 0–5 Nm.
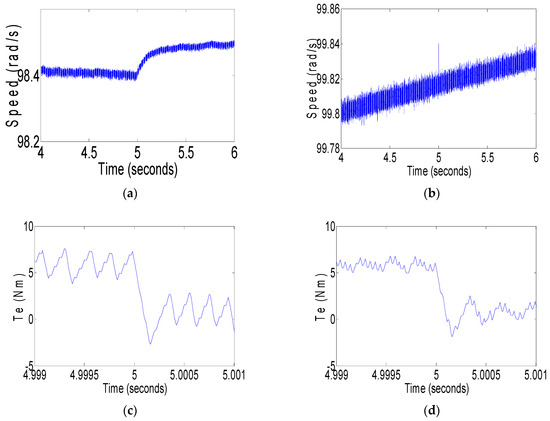
Figure 5.
(a) Speed response curve of PMSM under the traditional FOSMC for sudden loading form 5–0 Nm; (b) speed response curve of PMSM under the proposed HDFOSMC for sudden loading form 5–0 Nm; (c) torque response curve of PMSM under the traditional FOSMC for sudden loading form 5–0 Nm; (d) torque response curve of PMSM under the proposed HDFOSMC for sudden loading form 5–0 Nm.
The comparative analysis demonstrates the HDFOSMC framework’s advancement in PMSM control technology through its unified integration of precision, adaptability, and robustness. The comparison results across steady-state, dynamic, and disturbance-rejection scenarios highlight its architectural superiority:
- Steady-state precision: HDFOSMC achieves enhanced steady-state accuracy under nominal and loaded conditions, with suppressed residual oscillations and superior error attenuation compared to FOSMC.
- Dynamic tracking excellence: In sinusoidal and ramp reference tracking, HDFOSMC reduces tracking errors, preserves waveform fidelity, and enables faster transient stabilization through its fractional-order manifold design.
- Adaptive robustness: During abrupt load transitions and parametric variations, HDFOSMC exhibits accelerated error convergence, minimized speed deviations, and improved torque smoothness, coupled with enhanced harmonic disturbance rejection.
By reconciling conflicting performance objectives—precision, agility, and robustness—HDFOSMC establishes itself as a transformative solution for industrial applications demanding multi-domain control excellence, including semiconductor manufacturing and aerospace systems.
5. Discussion
This study presents a novel hybrid control architecture for the PMSM that addresses the dynamic–precision tradeoff in ultra-precision industrial systems. By integrating HDFOSMC with EPL, the framework achieves superior adaptive performance and control accuracy compared to traditional methods, particularly under varying operational conditions. The experimental results validate its enhanced transient response, steady-state precision, and robust stability across parameter fluctuations. Notably, it enables seamless adaptation to abrupt changes while maintaining sub-micron accuracy: a critical advantage for precision engineering. This breakthrough eliminates the historical compromise between agility and settling accuracy, establishing a new benchmark for adaptive motor control. The technology holds transformative potential for aerospace, robotics, and advanced manufacturing, enabling nanometer-scale stability in extreme operational environments. Practical deployment requires addressing three key challenges: First, the evolutionary learning mechanism introduces inherent computational demands that necessitate careful hardware–software co-design. Second, optimal performance relies on accurate real-time feedback; however, emerging sensor fusion techniques show promise in mitigating this dependency. Third, environmental disturbances such as mechanical vibration and thermal drift require complementary compensation strategies. In future practical applications, we will conduct further research on the aforementioned challenges.
Author Contributions
Conceptualization, P.G. and H.P.; methodology, P.G.; software, P.G.; validation, P.G., L.F. and H.P.; formal analysis, P.G.; investigation, P.G.; resources, P.G.; data curation, P.G.; writing—original draft preparation, P.G.; writing—review and editing, P.G., L.F. and H.P.; visualization, H.P.; supervision, L.F.; project administration, P.G. and L.F.; funding acquisition, P.G. and L.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Anhui Higher Education Institutions (grant number 2024AH040228), by the Outstanding Youth Scientific Research Project of Anhui Higher Education Institutions (grant number 2022AH020094), and by the Talent Research Start-up Fund of Tongling University (grant number 2022tlxyrc33, grant number 2022tlxyrc34).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors would like to express their gratitude to all those who helped them during the writing of this paper. The authors would like to thank the reviewers for their valuable comments and suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, G.; Yao, X.; Peretti, L.; Bai, J.; Gao, X.; Li, Z.; Huang, S. Smooth nonlinear ESO-based model-free predictive current control with an extended control set for SPMSM drives. IEEE J. Emerg. Sel. Top. Power Electron. 2025, 13, 2565–2579. [Google Scholar] [CrossRef]
- Mei, K.; Li, Q.; Chen, W.; Chen, C.C.; Ding, S. Modified discrete-time super-twisting control of PMSM speed regulation system: Theory and experimentation. IEEE Trans. Power Electron. 2025, 40, 7980–7993. [Google Scholar] [CrossRef]
- Lin, X.; Liu, J.; Liu, Z.; Gao, Y.; Peretti, L.; Wu, L. Model-free current predictive control for PMSMs with ultra-local model employing fixed-time observer and extremum-seeking method. IEEE Trans. Power Electron. 2025, 40, 10682–10693. [Google Scholar] [CrossRef]
- Cheng, Z.; Li, L.; Zhong, C.; Wang, J.; Bai, X.; Liu, J. Adaptive hybrid active disturbance rejection speed control for vehicle PMSM electric propulsion system under uncertain disturbances. IEEE Trans. Energy Convers. 2025. [Google Scholar] [CrossRef]
- Hong, J.; Lin, X.; Zhang, J.; Huang, W.; Yan, B.; Li, X. A composite sliding mode control with the first-order differentiator and sliding mode observer for permanent magnet synchronous machine. ISA Trans. 2024, 147, 489–500. [Google Scholar] [CrossRef]
- Li, Q.; Mei, K. A state-constrained second-order sliding mode control for permanent magnet synchronous motor drives. Nonlinear Dyn. 2024, 112, 12269–12282. [Google Scholar] [CrossRef]
- Fan, B.; Hu, Q.; Wang, J.; Zhao, Y.; Zhou, H.; Sun, L. Active disturbance observation rejection control based on port-controlled Hamiltonian with dissipation model for PMSM. Electr. Eng. 2025, 107, 2747–2757. [Google Scholar] [CrossRef]
- Wang, B.; Wang, S.; Peng, Y.; Pi, Y.; Luo, Y. Design and high-order precision numerical implementation of Fractional-order PI controller for PMSM speed system based on FPGA. Fractal Fract. 2022, 6, 218. [Google Scholar] [CrossRef]
- Dang, C.; Dou, M.; Yan, S.; Dang, M.; Wang, Y.; Zhao, D.; Hua, Z. An improved adaptive sliding mode speed control of PMSM drives with an extended state observer. IEEE Trans. Energy Convers. 2024, 39, 2349–2361. [Google Scholar] [CrossRef]
- Wang, S.; Li, B.; Chen, P.; Yu, W.; Peng, Y.; Luo, Y. A Fractional-order active disturbance rejection control for permanent magnet synchronous motor position servo system. Asian J. Control. 2024, 26, 3137–3147. [Google Scholar] [CrossRef]
- Dai, B.; Wang, Z. Disturbance observer-based sliding mode control using barrier function for output speed fluctuation constraints of PMSM. IEEE Trans. Energy Convers. 2024, 39, 1192–1201. [Google Scholar] [CrossRef]
- Zheng, W.; Chen, Y.; Wang, X.; Chen, Y.; Lin, M. Enhanced fractional order sliding mode control for a class of fractional order uncertain systems with multiple mismatched disturbances. ISA Trans. 2023, 133, 147–159. [Google Scholar] [CrossRef]
- Zhang, L.; Ma, J.; Wu, Q.; He, Z.; Qin, T.; Chen, C. Research on PMSM speed performance based on fractional order adaptive fuzzy backstepping control. Energies 2023, 16, 6922. [Google Scholar] [CrossRef]
- Chen, P.; Luo, Y. Analytical Fractional-order PID controller design with Bode’s ideal cutoff filter for PMSM speed servo system. IEEE Trans. Ind. Electron. 2022, 70, 1783–1793. [Google Scholar] [CrossRef]
- Pan, J. Fractional-order sliding mode control of manipulator combined with disturbance and state observer. Robot. Auton. Syst. 2025, 183, 104840. [Google Scholar] [CrossRef]
- Wu, J.; Xiong, H.; Pan, Z.; Deng, H. Fractional-order finite-time attitude control for underactuated quadrotors with dynamic event-triggered mechanism. Nonlinear Dyn. 2025, 113, 16721–16743. [Google Scholar] [CrossRef]
- Sheng, Y.; Gan, J.; Xia, L. Predefined-time Fractional-order time-varying sliding mode control and its application in hypersonic vehicle guidance law. Nonlinear Dyn. 2023, 111, 14177–14198. [Google Scholar] [CrossRef]
- Guha, D.; Roy, P.K.; Banerjee, S. Improved Fractional-order sliding mode controller for frequency regulation of a hybrid power system with nonlinear disturbance observer. IEEE Trans. Ind. Appl. 2023, 59, 4964–4979. [Google Scholar] [CrossRef]
- El Ferik, S.; Al-Qahtani, F.M.; Saif, A.W.A.; Al-Dhaifallah, M. Robust FOSMC of quadrotor in the presence of slung load. ISA Trans. 2023, 139, 106–121. [Google Scholar] [CrossRef]
- Long, B.; Mao, W.; Lu, P.; Rodriguez, J.; Guerrero, J.M.; Chong, K.T.; Teng, Y. Passivity Fractional-order sliding-mode control of grid-connected converter with LCL filter. IEEE Trans. Power Electron. 2023, 38, 6969–6982. [Google Scholar] [CrossRef]
- Sachan, S.; Swarnkar, P. Intelligent Fractional-order sliding mode optimised control of surgical manipulator for healthcare system. Electr. Eng. 2024, 106, 2131–2142. [Google Scholar] [CrossRef]
- Tadesse, A.B.; Ayele, E.A.; Olonje, A.O. Design and analysis of rate predictive Fractional-order sliding mode controller (RP-FOSMC) for MPPT and power regulation of DFIG-based wind energy conversion system (WECS). Energy Rep. 2022, 8, 11751–11768. [Google Scholar] [CrossRef]
- Zhang, B.; Pi, Y.; Luo, Y. Fractional order sliding-mode control based on parameters auto-tuning for velocity control of permanent magnet synchronous motor. ISA Trans. 2012, 51, 649–656. [Google Scholar] [CrossRef]
- Chaudhary, K.S.; Kumar, N. Fractional order fast terminal sliding mode control scheme for tracking control of robot manipulators. ISA Trans. 2023, 142, 57–69. [Google Scholar] [CrossRef]
- Ma, B.; Pei, W.; Zhang, Q.; Zhang, Y. Intelligent driving vehicle trajectory tracking control based on an improved Fractional-order super-twisting sliding mode control strategy. Int. J. Robust. Nonlinear Control 2025, 35, 1303–1316. [Google Scholar] [CrossRef]
- Kordkandi, R.D.; Hagh, M.T.; Roozbehani, S.; Feyzi, M.; Bayati, N.; Ebel, T. Reactive power control of micro-grids using FOSMC for grid code compliance during asymmetrical voltage sags. Electr. Power Syst. Res. 2024, 229, 110056. [Google Scholar] [CrossRef]
- Rahmani, M.; Redkar, S. Robot manipulator control using a robust data-driven method. Fractal Fract. 2023, 7, 692. [Google Scholar] [CrossRef]
- Al-Dhaifallah, M.; Al-Qahtani, F.M.; Elferik, S.; Saif, A.W.A. Quadrotor robust Fractional-order sliding mode control in unmanned aerial vehicles for eliminating external disturbances. Aerospace 2023, 10, 665. [Google Scholar] [CrossRef]
- Zhong, Y.; Lin, H.; Wang, J.; Chen, Z.; Yang, H. Speed fluctuation mitigation control for variable flux memory machine during magnetization state manipulations. IEEE Trans. Ind. Electron. 2022, 70, 222–232. [Google Scholar] [CrossRef]
- Li, C.; Deng, W. Remarks on fractional derivatives. Appl. Math. Comput. 2007, 187, 777–784. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Shu, H.; Zhu, D.; An, N.; Sang, Y.; Jiang, L. Perturbation observer based Fractional-order sliding-mode controller for MPPT of grid-connected PV inverters: Design and real-time implementation. Control Eng. Pract. 2018, 79, 105–125. [Google Scholar] [CrossRef]
- Qian, D.L. Stability Analysis and Normal Form Calculation of Fractional Differential Equations. Ph.D. Thesis, Shanghai University, Shanghai, China, 2010. [Google Scholar]
- Gao, P.; Pan, H. Model-free double Fractional-order integral sliding mode control for permanent magnet synchronous motor based electric mopeds drive system. IEICE Electron. Express 2023, 20, 20230178. [Google Scholar] [CrossRef]
- Long, Y.; Du, J. Adaptive position control strategy of SRM-based EMA system for precision position tracking. IEEE Trans. Transp. Electr. 2023, 9, 4680–4691. [Google Scholar] [CrossRef]
- Zaihidee, F.M.; Mekhilef, S.; Mubin, M. Application of fractional order sliding mode control for speed control of permanent magnet synchronous motor. IEEE Access 2019, 7, 101765–101774. [Google Scholar] [CrossRef]
- Özbek, N.S. Design and real-time implementation of a robust fractional second-order sliding mode control for an electromechanical system comprising uncertainties and disturbances. Eng. Sci. Technol. Int. J. 2022, 35, 101212. [Google Scholar] [CrossRef]
- Labbadi, M.; Boukal, Y.; Cherkaoui, M. Path following control of quadrotor UAV with continuous Fractional-order super twisting sliding mode. J. Intell. Robot. Syst. 2020, 100, 1429–1451. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).