Quantum Dynamics in a Comb Geometry: Green Function Solutions with Nonlocal and Fractional Potentials
Abstract
1. Introduction
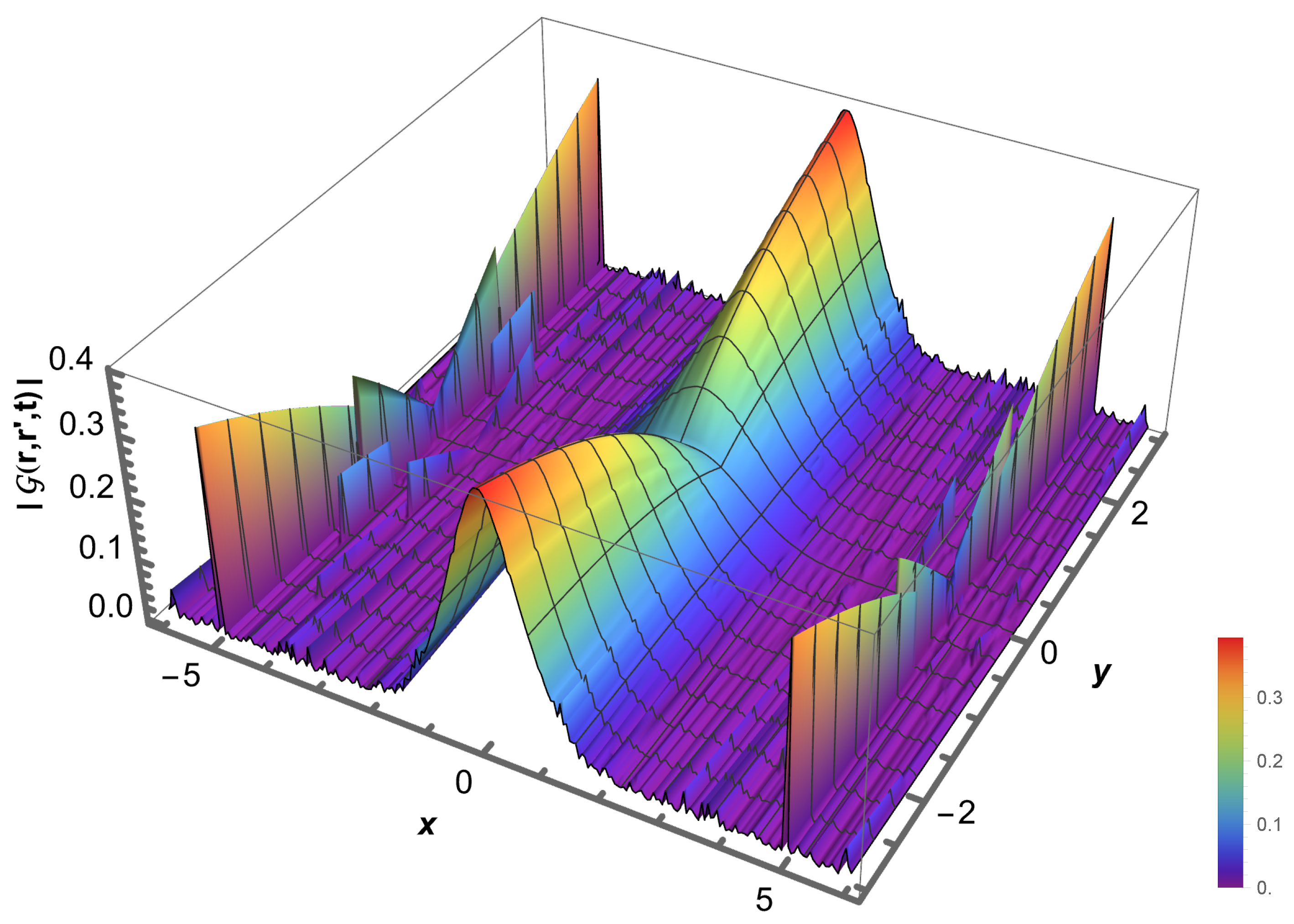
2. Schrödinger Equation in a Comb-Model
2.1. Nonlocal Dependence on Time
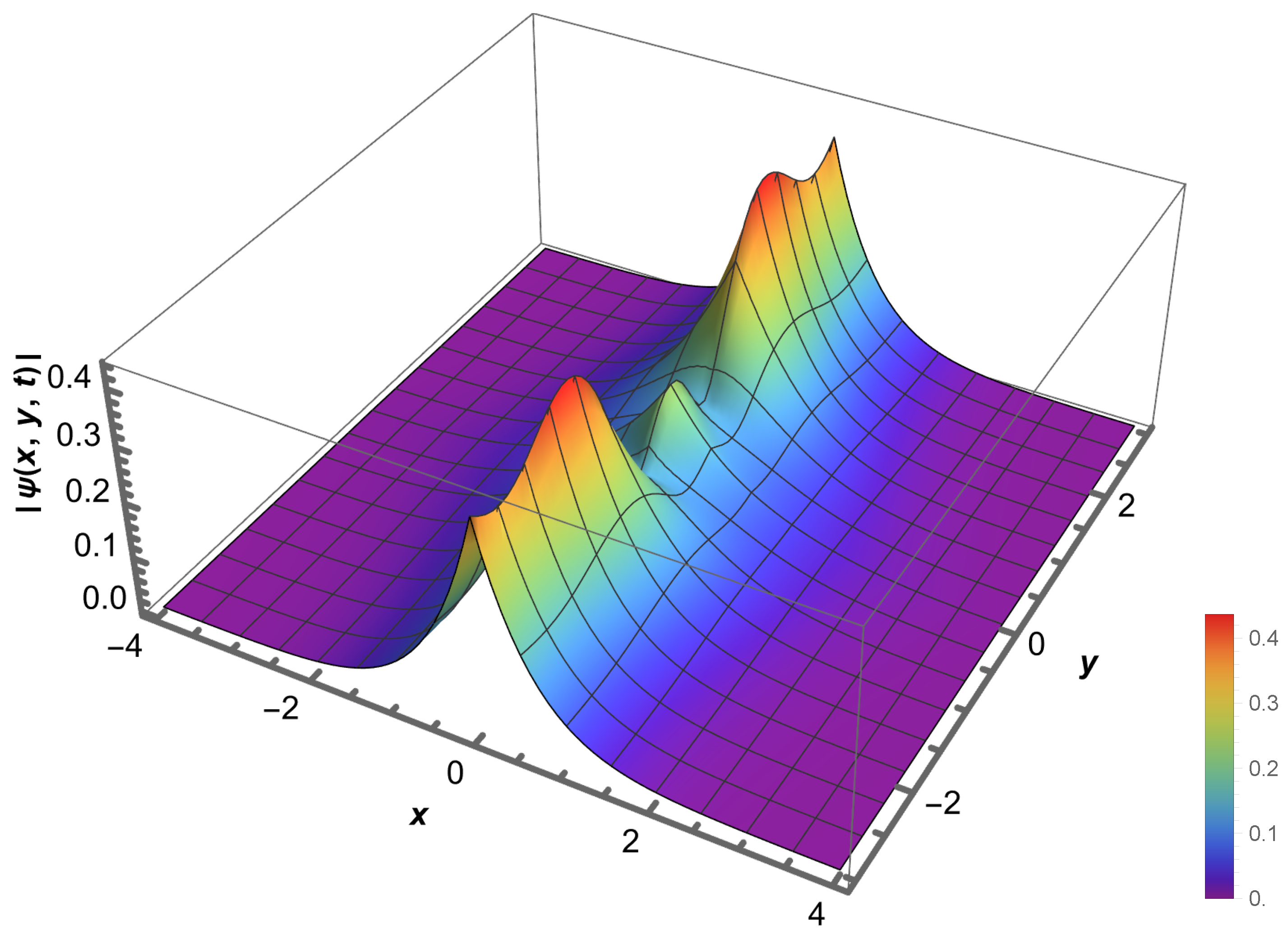
2.2. Nonlocal Dependence on Space and Time
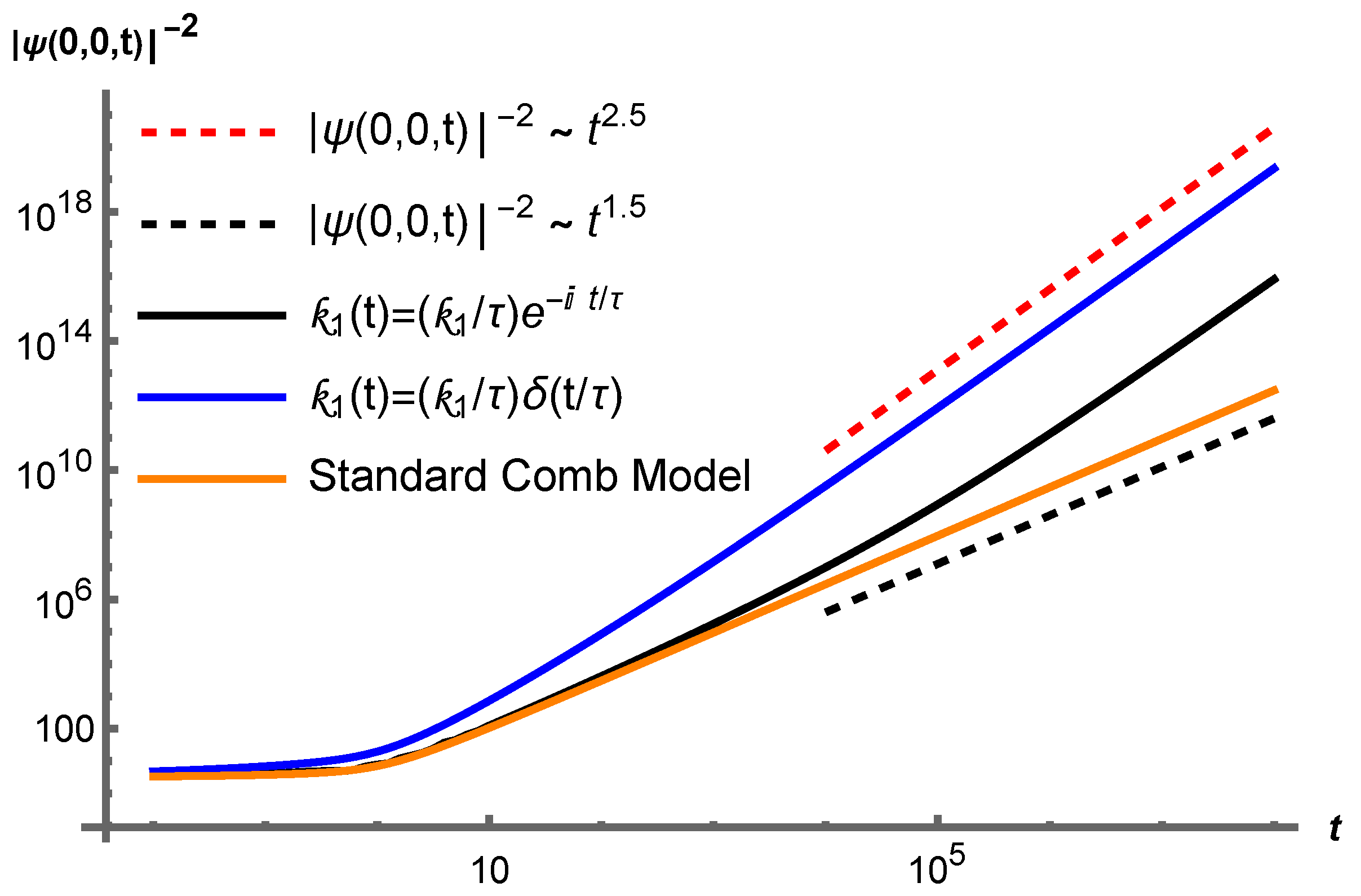
2.3. Nonlocal Dependence and Memory Kernels
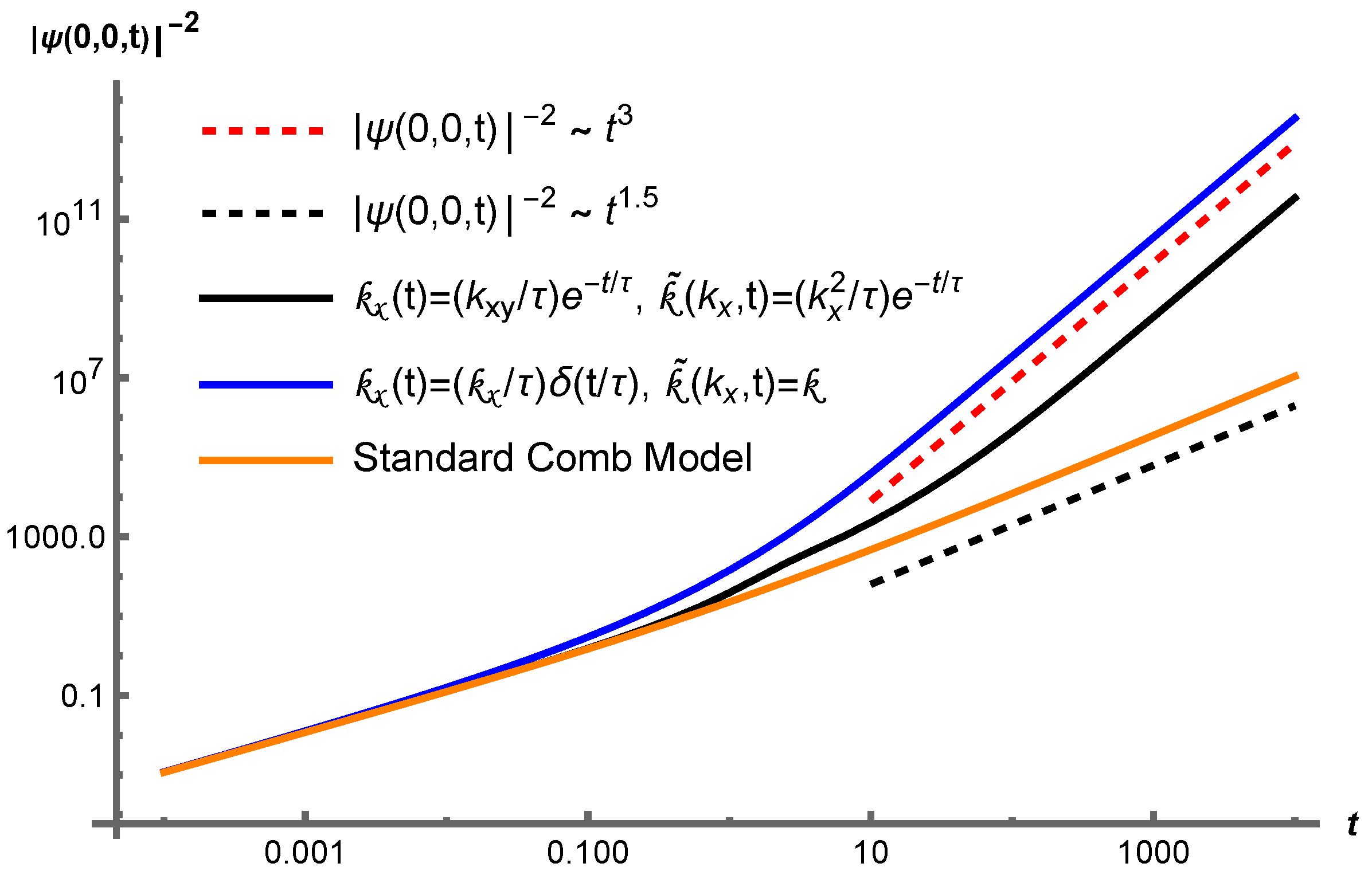
2.4. Fractional Spatial Operator and Nonlocal Terms
3. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sakurai, J.J.; Napolitano, J. Modern Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar] [CrossRef]
- Schrödinger, E. Quantisierung als Eigenwertproblem. Ann. Phys. 1926, 384, 489–527. [Google Scholar] [CrossRef]
- Schrödinger, E. Quantisierung als Eigenwertproblem. Ann. Phys. 1926, 384, 361–376. [Google Scholar] [CrossRef]
- Gabrick, E.; Sayari, E.; de Castro, A.; Trobia, J.; Batista, A.; Lenzi, E. Fractional Schrödinger equation and time dependent potentials. Commun. Nonlinear Sci. Numer. Simul. 2023, 123, 107275. [Google Scholar] [CrossRef]
- Cohen-Tannoudji, C.; Diu, B.; Laloe, F. Quantum Mechanics; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Lenzi, E.K.; Gabrick, E.C.; Sayari, E.; de Castro, A.S.M.; Trobia, J.; Batista, A.M. Anomalous Relaxation and Three-Level System: A Fractional Schrödinger Equation Approach. Quantum Rep. 2023, 2023, 442–458. [Google Scholar] [CrossRef]
- Evangelista, L.R.; Lenzi, E.K. Fractional Diffusion Equations and Anomalous Diffusion; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Evangelista, L.R.; Ribeiro, H.V.; Magin, R.L. Schrödinger Equation with Geometric Constraints and Position-Dependent Mass: Linked Fractional Calculus Models. Quantum Rep. 2022, 4, 296–308. [Google Scholar] [CrossRef]
- Longhi, S. Fractional Schrödinger equation in optics. Opt. Lett. 2015, 40, 1117–1120. [Google Scholar] [CrossRef]
- Afek, G.; Davidson, N.; Kessler, D.A.; Barkai, E. Colloquium: Anomalous statistics of laser-cooled atoms in dissipative optical lattices. Rev. Mod. Phys. 2023, 95, 031003. [Google Scholar] [CrossRef]
- Laskin, N. Fractional Quantum Mechanics; World Scientific Publishing Company: Singapore, 2018. [Google Scholar]
- Naber, M. Time fractional Schrödinger equation. J. Math. Phys. 2004, 45, 3339–3352. [Google Scholar] [CrossRef]
- Cius, D.; Menon, L., Jr.; dos Santos, M.A.F.; de Castro, A.S.M.; Andrade, F.M. Unitary evolution for a two-level quantum system in fractional-time scenario. Phys. Rev. E 2022, 106, 054126. [Google Scholar] [CrossRef]
- Cius, D. Unitary description of the Jaynes-Cummings model under fractional-time dynamics. Phys. Rev. E 2025, 111, 024110. [Google Scholar] [CrossRef]
- Plastino, A.R.; Tsallis, C. Nonlinear Schroedinger equation in the presence of uniform acceleration. J. Math. Phsy. 2013, 54, 041505. [Google Scholar] [CrossRef]
- Schwämmle, V.; Nobre, F.D.; Tsallis, C. q-Gaussians in the porous-medium equation: Stability and time evolution. Eur. Phys. J. B 2008, 66, 537–546. [Google Scholar] [CrossRef]
- Serkin, V.N.; Hasegawa, A. Novel Soliton Solutions of the Nonlinear Schrödinger Equation Model. Phys. Rev. Lett. 2000, 85, 4502. [Google Scholar] [CrossRef] [PubMed]
- Rafiq, M.H.; Raza, N.; Jhangeer, A. Nonlinear dynamics of the generalized unstable nonlinear Schrödinger equation: A graphical perspective. Opt. Quantum Electron. 2023, 55, 628. [Google Scholar] [CrossRef]
- Ibrahim, S.; Baleanu, D. Classes of solitary solution for nonlinear Schrödinger equation arising in optical fibers and their stability analysis. Opt. Quantum Electron. 2023, 55, 1158. [Google Scholar] [CrossRef]
- Olavo, L.; Bakuzis, A.; Amilcar, R. Generalized Schrödinger equation using Tsallis entropy. Phys. A 1999, 271, 303–323. [Google Scholar] [CrossRef]
- Iomin, A. Subdiffusion on a fractal comb. Phys. Rev. E 2011, 83, 052106. [Google Scholar] [CrossRef]
- Baskin, E.; Iomin, A. Superdiffusion on a Comb Structure. Phys. Rev. Lett. 2004, 93, 120603. [Google Scholar] [CrossRef]
- Iomin, A.; Méndez, V.; Horsthemke, W. Fractional Dynamics in Comb-like Structures; World Scientific: Singapore, 2018. [Google Scholar] [CrossRef]
- Hefny, M.M.; Tawfik, A.M. Tempered fractional diffusion in comb-like structures with numerical investigation. Phys. Scr. 2023, 98, 125258. [Google Scholar] [CrossRef]
- Tateishi, A.A.; Ribeiro, H.V.; Sandev, T.; Petreska, I.; Lenzi, E.K. Quenched and annealed disorder mechanisms in comb models with fractional operators. Phys. Rev. E 2020, 101, 022135. [Google Scholar] [CrossRef]
- Sandev, T.; Iomin, A.; Kantz, H. Fractional diffusion on a fractal grid comb. Phys. Rev. E 2015, 91, 032108. [Google Scholar] [CrossRef] [PubMed]
- Masó-Puigdellosas, A.; Sandev, T.; Méndez, V. Random walks on comb-like structures under stochastic resetting. Entropy 2023, 25, 1529. [Google Scholar] [CrossRef] [PubMed]
- Trajanovski, P.; Jolakoski, P.; Kocarev, L.; Sandev, T. Ornstein–uhlenbeck process on three-dimensional comb under stochastic resetting. Mathematics 2023, 11, 3576. [Google Scholar] [CrossRef]
- Méndez, V.; Iomin, A. Comb-like models for transport along spiny dendrites. Chaos, Solitons Fractals 2013, 53, 46–51. [Google Scholar] [CrossRef]
- Iomin, A. Fractional-time Schrödinger equation: Fractional dynamics on a comb. Chaos Solitons Fractals 2011, 44, 348–352. [Google Scholar] [CrossRef]
- Witthaut, D.; Rapedius, K.; Korsch, J. The Nonlinear Schrödinger Equation for the Delta-Comb Potential: Quasi-Classical Chaos and Bifurcations of Periodic Stationary Solutions. J. Nonlinear Math. Phys. 2009, 16, 207–233. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, L.; Ge, Z.; Liu, Y.; Feng, L.; Wang, J. Numerical simulation of the two-dimensional fractional Schrödinger equation for describing the quantum dynamics on a comb with the absorbing boundary conditions. Commun. Nonlinear Sci. Numer. Simul. 2025, 140, 108407. [Google Scholar] [CrossRef]
- Lenzi, E.; Evangelista, L. Space–time fractional diffusion equations in d-dimensions. J. Math. Phys. 2021, 62, 083304. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Evangelista, L.R.; Zola, R.S.; Scarfone, A.M. Fractional Schrödinger equation for heterogeneous media and Lévy like distributions. Chaos Solitons Fractals 2022, 163, 112564. [Google Scholar] [CrossRef]
- Sandev, T.; Petreska, I.; Lenzi, E.K. Time-dependent Schrödinger-like equation with nonlocal term. J. Math. Phys. 2014, 55. [Google Scholar] [CrossRef]
- Petreska, I.; Trajanovski, P.; Sandev, T.; Rocha, J.A.A.; de Castro, A.S.M.; Lenzi, E.K. Solutions to the Schrödinger Equation: Nonlocal Terms and Geometric Constraints. Mathematics 2025, 13, 137. [Google Scholar] [CrossRef]
- Coz, M.; Arnold, L.G.; MacKellar, A.D. Nonlocal potentials and their local equivalents. Ann. Phys. 1970, 59, 219–247. [Google Scholar] [CrossRef]
- Li, C.; Wan, L.; Wei, Y.; Wang, J. Definition of current density in the presence of a non-local potential. Nanotechnology 2008, 19, 155401. [Google Scholar] [CrossRef]
- Chechkin, A.V.; Metzler, R.; Klafter, J.; Gonchar, V.Y. Introduction to the theory of Lévy flights. In Anomalous Transport: Foundations and Applications; John Wiley & Sons, Ltd.: Weinheim, Germany, 2008; pp. 129–162. [Google Scholar] [CrossRef]
- Allegrini, P.; Grigolini, P.; West, B.J. Dynamical approach to Lévy processes. Phys. Rev. E 1996, 54, 4760–4767. [Google Scholar] [CrossRef]
- Ali, I.; Kalla, S. A generalized Hankel transform and its use for solving certain partial differential equations. ANZIAM J. 1999, 41, 105–117. [Google Scholar] [CrossRef][Green Version]
- Garg, M.; Rao, A.; Kalla, S.L. On a generalized finite Hankel transform. Appl. Math. Comput. 2007, 190, 705–711. [Google Scholar] [CrossRef]
- Nakhi, Y.B.; Kalla, S.L. Some boundary value problems of temperature fields in oil strata. Appl. Math. Comput. 2003, 146, 105–119. [Google Scholar] [CrossRef]
- Xie, K.; Wang, Y.; Wang, K.; Cai, X. Application of Hankel transforms to boundary value problems of water flow due to a circular source. Appl. Math. Comput. 2010, 216, 1469–1477. [Google Scholar] [CrossRef]
- Einevoll, G.; Hemmer, P.; Thomsen, J. Operator ordering in effective-mass theory for heterostructures. I. Comparison with exact results for superlattices, quantum wells, and localized potentials. Phys. Rev. B 1990, 42, 3485. [Google Scholar] [CrossRef]
- Einevoll, G. Operator ordering in effective-mass theory for heterostructures. II. Strained systems. Phys. Rev. B 1990, 42, 3497. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. A generalized self-consistent approach to study position-dependent mass in semiconductors organic heterostructures and crystalline impure materials. Phys. E Low-Dimens. Syst. Nanostruct. 2020, 124, 114295. [Google Scholar] [CrossRef]
- Cao, L.q.; Luo, J.l.; Wang, C.y. Multiscale analysis and numerical algorithm for the Schrödinger equations in heterogeneous media. Appl. Math. Comput. 2010, 217, 3955–3973. [Google Scholar] [CrossRef]
- Arvedson, E.; Wilkinson, M.; Mehlig, B.; Nakamura, K. Staggered ladder spectra. Phys. Rev. Lett. 2006, 96, 030601. [Google Scholar] [CrossRef] [PubMed]
- Mota-Furtado, F.; O’Mahony, P.F. Exact propagator for generalized Ornstein-Uhlenbeck processes. Phys. Rev. E 2007, 75, 041102. [Google Scholar] [CrossRef][Green Version]
- Mota-Furtado, F.; O’Mahony, P. Eigenfunctions and matrix elements for a class of eigenvalue problems with staggered ladder spectra. Phys. Rev. A 2006, 74, 044102. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gabrick, E.C.; Lenzi, E.K.; de Castro, A.S.M.; Trobia, J.; Batista, A.M. Quantum Dynamics in a Comb Geometry: Green Function Solutions with Nonlocal and Fractional Potentials. Fractal Fract. 2025, 9, 446. https://doi.org/10.3390/fractalfract9070446
Gabrick EC, Lenzi EK, de Castro ASM, Trobia J, Batista AM. Quantum Dynamics in a Comb Geometry: Green Function Solutions with Nonlocal and Fractional Potentials. Fractal and Fractional. 2025; 9(7):446. https://doi.org/10.3390/fractalfract9070446
Chicago/Turabian StyleGabrick, Enrique C., Ervin K. Lenzi, Antonio S. M. de Castro, José Trobia, and Antonio M. Batista. 2025. "Quantum Dynamics in a Comb Geometry: Green Function Solutions with Nonlocal and Fractional Potentials" Fractal and Fractional 9, no. 7: 446. https://doi.org/10.3390/fractalfract9070446
APA StyleGabrick, E. C., Lenzi, E. K., de Castro, A. S. M., Trobia, J., & Batista, A. M. (2025). Quantum Dynamics in a Comb Geometry: Green Function Solutions with Nonlocal and Fractional Potentials. Fractal and Fractional, 9(7), 446. https://doi.org/10.3390/fractalfract9070446






