Pell and Pell–Lucas Sequences of Fractional Order

Abstract

The purpose of this paper is to introduce the fractional Pell numbers, together with several properties, via a Grünwald–Letnikov fractional operator of orders $q\in (0,1)$ and $q\in (1,2)$. This paper also explores the fractional Pell–Lucas numbers and their properties.Due to the long-term memory property, fractional Pell sequences and fractional Pell–Lucas sequences present potential applications in modeling and computation. The closed form is deduced, and the numerical schemes are determined. The fractional characteristic equation is introduced, and it is shown that its solutions include a fractional silver ratio depending on the fractional order. In addition, the tiling problem and the concept of the fractional silver spiral are considered.A MATLAB program for applying the use of the fractional silver ratio is presented.

1. Introduction

The Pell numbers are named after English mathematician John Pell (1611–1685). Details about Pell can be found in, e.g., [1,2,3], while some properties can be found in [4]. Pell numbers may be calculated by means of a recurrence relation similar to that for the Fibonacci numbers. Pell–Lucas numbers, or companion Pell numbers, are defined similarly to the Pell numbers by recurrence relation, the difference consisting of the initial condition.

Background on fractional calculus and fractional differences can be found in, e.g., [5,6,7,8], while an appropriate bibliography for the fractional q-calculus is provided in [9].

This paper continues the work started in [10], where the Fibonacci’s numbers of fractional order were introduced and analyzed.

The Fibonacci numbers are the most famous example of a linear recurrence relation. Both the Fibonacci and Pell sequences are interesting recursively defined sequences, but they differ significantly in their prominence and application across different fields. So, compared with Pell sequences that arise in number theory, particularly in Pell’s equation $x^2-2y^2=1$, or continuous fractions of square roots, Fibonacci sequences have far wider and deeper mathematical exposure (e.g., in number theory, combinatorics, algebra, and geometry). Also, in computer science, Fibonacci’s numbers are common in algorithm design and data structures and used in teaching recursion, dynamic programming, and time complexity, while Pell’s numbers might be used only in niche recurrence problems compared to Fibonacci’s numbers. These sequences serve as benchmarks for solving recurrence relations (e.g., via characteristic equations). They illustrate the impact of initial conditions and coefficients on closed-form solutions. However, in domains like number theory, continuous fractions, cryptography, algebraic number theory, and theoretical physics, Fibonacci sequences are more widespread. Fractional Pell sequences serve as recursive structures for developing fractional difference methods with better accuracy in modeling anomalous dynamics. They can help to generate generalized orthogonal polynomials for spectral methods, which are helpful in numerical PDE solvers. Fractional Pell sequences possess long-term memory due to fractional-order recursions. So, they can be applied in viscoelastic materials, anomalous diffusion, fractional-order delay systems, wave propagation in fractal media, biological growth and branching processes, as well as in neural networks, viscoelastic materials, epidemiology, and finance. These sequences can also solve fractional dynamic equations on time scales, giving rise to new special functions and stability behaviors. Introducing fractional versions of Fibonacci and Pell numbers enables new analytical tools and models in discrete fractional calculus. However, their usefulness would depend on whether they provide meaningful insights or solve problems that classical discrete sequences cannot.

Some of the properties of Pell’s numbers have been shown to be demonstrable by the fractional approach, such as the property that the silver ratio can be expressed as the ratio of two consecutive Pell numbers, the deduction of the characteristic equation generating the fractional silver ratio, or the deduction of the closed (explicit) form of fractional Pell numbers. Similarly to the fractional golden ratio determined via the fractional Fibonacci numbers, where the fractional golden spiral is used to cover the tiling with fractional Fibonacci numbers, the fractional Pell numbers are used to generate the fractional silver spiral covering a square tiling. While previous studies [11,12] showed thatthe generalization of discrete systems via a fractional approach breaks the symmetry, in this article, it is shown that the symmetry is not destroyed by the use of a silver ratio or golden ratio of fractional order.

Among the various definitions for fractional differences, the most widely used are the Grünwald–Letnikov, the Riemann–Liouville, and the Caputo definitions.Among the three definitions, the Grünwald–Letnikov definition, which stems from the limitation of integer-order difference, plays an outstanding role in numerical calculation. It also provides the discrete approximation of a fractional derivative. Moreover, the definitions for fractional sum and differences can be expressed in a unified manner. The Caputo approach is equivalent to the Grünwald–Letnikov approach in the case of homogeneous initial conditions. However, in the case of inhomogeneous initial conditions, both approaches are not the same (in the context of fractional sequences and their applications; see, e.g., [13,14,15,16,17,18,19]).

This paper is structured as follows: Section 2 presents the utilized notions in the paper; Section 3 introduces the fractional Pell numbers with the closed explicit form, the numerical scheme, the fractional silver ratio, and some related properties; Section 4 deals with the fractional Pell–Lucas numbers, explicit form, and numerical scheme; Section 5 concludes the manuscript; and Appendix A presents a MATLAB (https://www.mathworks.com/products/matlab.html, accessed on 21 June 2025) script generating a pinecone.

2. Preliminaries

We shall use the following fundamentals of discrete fractional calculus throughout the article. For any $a\in \mathbb{R}$, denote by ${\mathbb{N}}_a=\{a,a+1,a+2,\dots \}$.

Definition 1

([20]). The Pell numbers are defined by the recurrence relation

$$\begin{array}{c}P\left(0\right)=0,P\left(1\right)=1,\end{array}$$

(1)

$$\begin{array}{c}P(n+2)=P\left(n\right)+2P(n+1),n\in {\mathbb{N}}_0.\end{array}$$

(2)

The first terms are

$$0,1,2,5,12,29,70,169,408,985,2378,5741,13860,\dots$$

Definition 2

([20]). The Pell–Lucas numbers are defined by the recurrence relation

$$\begin{array}{c}Q\left(0\right)=2,Q\left(1\right)=2,\end{array}$$

(3)

$$\begin{array}{c}Q(n+2)=Q\left(n\right)+2Q(n+1),n\in {\mathbb{N}}_0,\end{array}$$

(4)

with the first terms

$$2,2,6,14,34,82,198,478,1154,2786,6726,16238,39202,\dots$$

Definition 3

([21]). Let $u:{\mathbb{N}}_a\to \mathbb{R}$. The first-order nabla difference of u is defined by

$$\nabla u\left(n\right)=u\left(n\right)-u(n-1),n\in {\mathbb{N}}_{a+1},$$

and the second-order nabla difference of u is defined by

$${\nabla }^{2}u\left(n\right)=u\left(n\right)-2u(n-1)+u(n-2),n\in {\mathbb{N}}_{a+2}.$$

Definition 4

([7]). The Euler gamma function is defined by

$$\mathrm{\Gamma }\left(z\right)={\int }_0^{\infty }{e}^{-s}{s}^{z-1}ds,\Re \left(z\right)>0.$$

Using the reduction formula

$$\mathrm{\Gamma }(z+1)=z\mathrm{\Gamma }\left(z\right),\Re \left(z\right)>0,$$

the Euler gamma function can also be extended to the half-plane $\Re \left(z\right)\le 0$, except for $z\in \{\dots ,-2,-1,0\}$.

Definition 5

([22]). Let $u:{\mathbb{N}}_a\to \mathbb{R}$ and $\nu \in \mathbb{R}$. The ${\nu }^{\mathit{th}}$ Grünwald–Letnikov fractional difference/sum of u based on a is given by

$${\nabla }_a^{\nu }u\left(n\right)={\displaystyle \frac{1}{\mathrm{\Gamma }(-\nu )}}\sum _{s=a}^n{\displaystyle \frac{\mathrm{\Gamma }(n-s-\nu )}{\mathrm{\Gamma }(n-s+1)}}u\left(s\right),n\in {\mathbb{N}}_a.$$

3. Fractional Pell Sequence

A two-dimensional system of linear difference equations that describes (2) is

$$\left(\begin{array}{c}P(n+2)\\ P(n+1)\end{array}\right)=\left(\begin{array}{cc}2& 1\\ 1& 0\end{array}\right)\left(\begin{array}{c}P(n+1)\\ P\left(n\right)\end{array}\right),n\in {\mathbb{N}}_0.$$

Then,

$$\left(\begin{array}{c}\nabla P(n+2)\\ \nabla P(n+1)\end{array}\right)=\left(\begin{array}{cc}1& 1\\ 1& -1\end{array}\right)\left(\begin{array}{c}P(n+1)\\ P\left(n\right)\end{array}\right),n\in {\mathbb{N}}_0.$$

Consequently, we have the following initial value problem

$$\begin{array}{c}\nabla \overline{P}\left(n\right)=A\overline{P}(n-1),n\in {\mathbb{N}}_1,\end{array}$$

(5)

$$\begin{array}{c}\overline{P}\left(0\right)={\overline{P}}_0,\end{array}$$

(6)

associated with the Pell numbers. Here,

$$\begin{array}{cc}\hfill \overline{P}\left(n\right)& =\left(\begin{array}{c}P(n+1)\\ P\left(n\right)\end{array}\right),\hfill \\ \hfill A& =\left(\begin{array}{cc}1& 1\\ 1& -1\end{array}\right),\hfill \\ \hfill {\overline{P}}_0& =\left(\begin{array}{c}P\left(1\right)\\ P\left(0\right)\end{array}\right)=\left(\begin{array}{c}1\\ 0\end{array}\right).\hfill \end{array}$$

Now, for $0<q<1$, we consider the $q^{\mathrm{th}}$-order difference equation

$${\nabla }_0^q\overline{x}\left(n\right)=A\overline{x}(n-1),n\in {\mathbb{N}}_1,$$

(7)

together with the initial condition

$$\overline{x}\left(0\right)=\left(\begin{array}{c}1\\ 0\end{array}\right),$$

(8)

analogous to (5) and (6). Here,

$$\overline{x}\left(n\right)=\left(\begin{array}{c}x(n+1)\\ x\left(n\right)\end{array}\right),A=\left(\begin{array}{cc}1& 1\\ 1& -1\end{array}\right).$$

3.1. The Solution of the Initial Value Problem (7) and (8)

Theorem 1.

The unique solution of (7) and (8) is given by

$$\overline{x}\left(n\right)=\sum _{k=0}^n{A}^k{\displaystyle \frac{\mathrm{\Gamma }(n-k+kq+q)}{\mathrm{\Gamma }(n-k+1)\mathrm{\Gamma }(kq+q)}}\overline{x}\left(0\right),n\in {\mathbb{N}}_0.$$

(9)

Proof. 

Denote by

$$u\left(n\right)=\sum _{k=0}^n{A}^k{\displaystyle \frac{\mathrm{\Gamma }(n-k+kq+q)}{\mathrm{\Gamma }(n-k+1)\mathrm{\Gamma }(kq+q)}},n\in {\mathbb{N}}_0.$$

First, we show that u satisfies the fractional difference equation

$${\nabla }_0^{q}u\left(n\right)=Au(n-1),n\in {\mathbb{N}}_1.$$

(10)

To see this, for $n\in {\mathbb{N}}_1$, consider

$$\begin{array}{cc}\hfill {\nabla }_0^{q}u\left(n\right)& ={\displaystyle \frac{1}{\mathrm{\Gamma }(-q)}}\sum _{s=0}^n{\displaystyle \frac{\mathrm{\Gamma }(n-s-q)}{\mathrm{\Gamma }(n-s+1)}}u\left(s\right)\left(\mathrm{By}\mathrm{Definition}5\right)\hfill \\ & ={\displaystyle \frac{1}{\mathrm{\Gamma }(-q)}}\sum _{s=0}^n{\displaystyle \frac{\mathrm{\Gamma }(n-s-q)}{\mathrm{\Gamma }(n-s+1)}}\left[\sum _{k=0}^s{A}^k{\displaystyle \frac{\mathrm{\Gamma }(s-k+kq+q)}{\mathrm{\Gamma }(s-k+1)\mathrm{\Gamma }(kq+q)}}\right]\hfill \\ & =\sum _{k=0}^n{A}^k\left[\sum _{s=k}^n{\displaystyle \frac{\mathrm{\Gamma }(n-s-q)}{\mathrm{\Gamma }(n-s+1)\mathrm{\Gamma }(-q)}}{\displaystyle \frac{\mathrm{\Gamma }(s-k+kq+q)}{\mathrm{\Gamma }(s-k+1)\mathrm{\Gamma }(kq+q)}}\right]\hfill \\ & =\sum _{k=0}^n{A}^k{\displaystyle \frac{\mathrm{\Gamma }(n-k+kq)}{\mathrm{\Gamma }(n-k+1)\mathrm{\Gamma }\left(kq\right)}}\hfill \\ & =\sum _{k=1}^n{A}^k{\displaystyle \frac{\mathrm{\Gamma }(n-k+kq)}{\mathrm{\Gamma }(n-k+1)\mathrm{\Gamma }\left(kq\right)}}\hfill \\ & =A\sum _{k=0}^{n-1}{A}^k{\displaystyle \frac{\mathrm{\Gamma }(n-1-k+kq+q)}{\mathrm{\Gamma }(n-1-k+1)\mathrm{\Gamma }(kq+q)}}\hfill \\ & =Au(n-1),\hfill \end{array}$$

implying that (10) holds. Therefore, any solution of (7) is of the form

$$\overline{x}\left(n\right)=u\left(n\right)c,n\in {\mathbb{N}}_0,$$

where c is any constant vector. Since $u\left(0\right)=I$, we obtain $c=\overline{x}\left(0\right)$. Thus, the unique solution of the initial value problem (7) and (8) is given by (9).    □

3.2. Closed-Form Expression of Fractional Pell Sequence

The following result is the generalization of Binet’s formula for the fractional Pell numbers.

Theorem 2.

The closed-form expression of the fractional Pell sequence is given by

$$x\left(n\right)={\displaystyle \frac{1}{2\phi }}\sum _{k=0}^n\left[{\phi }^k-{\left(-\phi \right)}^k\right]{\displaystyle \frac{\mathrm{\Gamma }(n-k+kq+q)}{\mathrm{\Gamma }(n-k+1)\mathrm{\Gamma }(kq+q)}},n\in {\mathbb{N}}_0.$$

Here, ${\displaystyle \phi =\sqrt{2}}$.

Proof. 

The eigenvalues of A are $\phi$ and $-\phi$. The corresponding eigenvectors are $\left(\begin{array}{c}1\\ \phi -1\end{array}\right)$ and $\left(\begin{array}{c}1\\ -\phi -1\end{array}\right)$, respectively. Now, we diagonalize the matrix A through the use of its eigendecomposition:

$$A=S\mathrm{\Omega }{S}^{-1},$$

and

$$A^k=S{\mathrm{\Omega }}^k{S}^{-1},k=1,2,\dots ,n,$$

where

$$\mathrm{\Omega }=\left(\begin{array}{cc}\phi & 0\\ 0& -\phi \end{array}\right),S=\left(\begin{array}{cc}1& 1\\ \phi -1& -\phi -1\end{array}\right).$$

Consequently, from (9), we have

$$\overline{x}\left(n\right)=\sum _{k=0}^n\left[S{\mathrm{\Omega }}^k{S}^{-1}\overline{x}\left(0\right)\right]{\displaystyle \frac{\mathrm{\Gamma }(n-k+kq+q)}{\mathrm{\Gamma }(n-k+1)\mathrm{\Gamma }(kq+q)}},n\in {\mathbb{N}}_0.$$

For $k=0,1,\dots ,n$, consider

$$\begin{array}{cc}\hfill S{\mathrm{\Omega }}^k{S}^{-1}& =\left(\begin{array}{cc}1& 1\\ \phi -1& -\phi -1\end{array}\right){\left(\begin{array}{cc}\phi & 0\\ 0& -\phi \end{array}\right)}^k{\left(\begin{array}{cc}1& 1\\ \phi -1& -\phi -1\end{array}\right)}^{-1}\hfill \\ & =-{\displaystyle \frac{1}{2\phi }}\left(\begin{array}{cc}1& 1\\ \phi -1& -\phi -1\end{array}\right)\left(\begin{array}{cc}{\phi }^k& 0\\ 0& {\left(-\phi \right)}^k\end{array}\right)\left(\begin{array}{cc}-\phi -1& -1\\ -\phi +1& 1\end{array}\right).\hfill \end{array}$$

Since $\overline{x}\left(n\right)=\left(\begin{array}{c}x(n+1)\\ x\left(n\right)\end{array}\right)$, the closed form, which is an explicit expression for the nth element in the fractional Pell sequence, is given by

$$x\left(n\right)={\displaystyle \frac{1}{2\phi }}\sum _{k=0}^n\left[{\phi }^k-{\left(-\phi \right)}^k\right]{\displaystyle \frac{\mathrm{\Gamma }(n-k+kq+q)}{\mathrm{\Gamma }(n-k+1)\mathrm{\Gamma }(kq+q)}},$$

for $n\in {\mathbb{N}}_0$.    □

Remark 1.

For $q=1$, we obtain the expression of the closed integer-order (IO) form for the nth element in Pell sequences (1) and (2) as follows:

$$\begin{array}{cc}\hfill x\left(n\right)& ={\displaystyle \frac{1}{2\phi }}\sum _{k=0}^n\left[{\phi }^k-{\left(-\phi \right)}^k\right]{\displaystyle \frac{\mathrm{\Gamma }(n+1)}{\mathrm{\Gamma }(n-k+1)\mathrm{\Gamma }(k+1)}}\hfill \\ \hfill & ={\displaystyle \frac{1}{2\phi }}\sum _{k=0}^n\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right){\phi }^k-{\displaystyle \frac{1}{2\phi }}\sum _{k=0}^n\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right){\left(-\phi \right)}^k\hfill \\ \hfill & ={\displaystyle \frac{1}{2\phi }}{\left(1+\phi \right)}^n-{\displaystyle \frac{1}{2\phi }}{\left(1-\phi \right)}^n\hfill \\ \hfill & ={\displaystyle \frac{1}{2\sqrt{2}}}\left[{\left(1+\sqrt{2}\right)}^n-{\left(1-\sqrt{2}\right)}^n\right],\hfill \end{array}$$

for $n\in {\mathbb{N}}_0$.

Theorem 3.

$x\left(n\right)>0$ for all $n\in {\mathbb{N}}_1$.

Proof. 

Clearly, $x\left(1\right)=1>0$. From (7), we have

$${\nabla }_0^{q}x(n+1)=x\left(n\right)+x(n-1),n\in {\mathbb{N}}_1.$$

(11)

Expanding the left-hand side of (11) using Definition 5 and rearranging the terms, we get

$$\begin{array}{cc}\hfill x(n+1)& =x\left(n\right)+x(n-1)-{\displaystyle \frac{1}{\mathrm{\Gamma }(-q)}}\sum _{j=0}^n{\displaystyle \frac{\mathrm{\Gamma }(n-j-q+1)}{\mathrm{\Gamma }(n-j+2)}}x\left(j\right)\hfill \\ & =x\left(n\right)+x(n-1)+{\displaystyle \frac{q}{\mathrm{\Gamma }(1-q)}}\sum _{j=0}^n{\displaystyle \frac{\mathrm{\Gamma }(n-j-q+1)}{\mathrm{\Gamma }(n-j+2)}}x\left(j\right),\hfill \end{array}$$

for $n\in {\mathbb{N}}_1$. Since $\mathrm{\Gamma }(1-q)>0$, $\mathrm{\Gamma }(n-j-q+1)>0$ and $\mathrm{\Gamma }(n-j+2)>0$ for all $0\le j\le n$ and $n\in {\mathbb{N}}_1$, it successively follows that $x(n+1)>0$ for all $n\in {\mathbb{N}}_1$.    □

3.3. Numerical Scheme for the Fractional Pell Sequence

To obtain the numerical integral for the fractional Pell sequence, one rewrites (2) in the normal form, one replaces the classical ∇ difference operator with the Grünwald–Letnikov fractional difference operator, one expands the Grünwald–Letnikov fractional difference operator, and, finally, one rearranges the terms to express $x\left(n\right)$.

Using Definition 3, (2) can be rewritten as

$${\nabla }^{2}P\left(n\right)=f\left(P(n-1),P(n-2)\right),n\in {\mathbb{N}}_2,$$

(12)

where

$$f\left(P(n-1),P(n-2)\right)=2P(n-2),n\in {\mathbb{N}}_2.$$

Now, for $1<q<2$, we consider the $q^{\mathrm{th}}$-order difference equation

$${\nabla }_0^{q}x\left(n\right)=f\left(x(n-1),x(n-2)\right),n\in {\mathbb{N}}_2,$$

(13)

together with the initial condition

$$x\left(0\right)=0,x\left(1\right)=1,$$

analogous to (1)–(12).

Theorem 4.

The numerical scheme for the fractional Pell sequence is given by

$$\begin{array}{c}x\left(n\right)=qx(n-1)+\left[2-{\displaystyle \frac{q(q-1)}{2}}\right]x(n-2)\hfill \\ \hfill -\sum _{j=0}^{n-3}{\displaystyle \frac{\mathrm{\Gamma }(n-j-q)}{\mathrm{\Gamma }(n-j+1)\mathrm{\Gamma }(-q)}}x\left(j\right),n\in {\mathbb{N}}_2.\end{array}$$

(14)

Proof. 

From Definition 5, we have

$$\begin{array}{cc}\hfill {\nabla }_0^{q}x\left(n\right)& =\sum _{j=0}^n{\displaystyle \frac{\mathrm{\Gamma }(n-j-q)}{\mathrm{\Gamma }(n-j+1)\mathrm{\Gamma }(-q)}}x\left(j\right)\hfill \\ & =x\left(n\right)-qx(n-1)+{\displaystyle \frac{q(q-1)}{2}}x(n-2)+\sum _{j=0}^{n-3}{\displaystyle \frac{\mathrm{\Gamma }(n-j-q)}{\mathrm{\Gamma }(n-j+1)\mathrm{\Gamma }(-q)}}x\left(j\right).\hfill \end{array}$$

(15)

Using (15) in (13) and rearranging the terms, we obtain

$$\begin{array}{c}\hfill x\left(n\right)=f(x(n-1),x(n-2))+qx(n-1)-{\displaystyle \frac{q(q-1)}{2}}x(n-2)\\ \hfill -\sum _{j=0}^{n-3}{\displaystyle \frac{\mathrm{\Gamma }(n-j-q)}{\mathrm{\Gamma }(n-j+1)\mathrm{\Gamma }(-q)}}x\left(j\right),n\in {\mathbb{N}}_2.\end{array}$$

That is,

$$\begin{array}{c}x\left(n\right)=qx(n-1)+\left[2-{\displaystyle \frac{q(q-1)}{2}}\right]x(n-2)\hfill \\ \hfill -\sum _{j=0}^{n-3}{\displaystyle \frac{\mathrm{\Gamma }(n-j-q)}{\mathrm{\Gamma }(n-j+1)\mathrm{\Gamma }(-q)}}x\left(j\right),n\in {\mathbb{N}}_2.\end{array}$$

   □

In Table 1, the fractional Pell sequences are presented for $q=1.99$, $q=1.995$, $q=1.999$, and $q=2$ (IO), respectively.

Table 1. Fractional Pell sequences for $q=1.99$, $q=1.995$, $q=1.999$, and IO ($q=2$), respectively.

#	$\mathit{q}=1.99$	$\mathit{q}=1.995$	$\mathit{q}=1.999$	IO
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15	0 1 1.99000000000 4.97505000000 11.92008817890 28.77036010178 69.35116600455 167.20881853340 403.13188359617 971.93524756072 2343.28804106191 5649.51967020207 13620.45119203567 32836.32193044393 79147.45145012428	0 1 1.99500000000 4.98751250000 11.96001913091 28.88507358306 69.67521980455 168.10317529800 405.56193312317 978.45500806016 2360.60539480727 5695.14417610542 13739.88521182454 33147.66861641826 79961.75170649997	0 1 1.99900000000 4.99750050000 11.99199983283 28.97699771786 69.93498596635 168.82043801696 407.51174632077 983.68898580072 2374.51490469204 5731.81033968845 13835.92258701109 33398.17489180408 80617.47387422606	0 1 2 5 12 29 70 169 408 985 2378 5741 13860 33461 80782

Remark 2.

We make the following observations:

(i) 

For $n\in {\mathbb{N}}_3$ and $0\le j\le n-3$, consider

$${\displaystyle \frac{\mathrm{\Gamma }(n-j-q)}{\mathrm{\Gamma }(n-j+1)\mathrm{\Gamma }(-q)}}=q(q-1){\displaystyle \frac{\mathrm{\Gamma }(n-j-q)}{\mathrm{\Gamma }(n-j+1)\mathrm{\Gamma }(2-q)}}.$$

Clearly, by [7], $\mathrm{\Gamma }(n-j-q)>0$, $\mathrm{\Gamma }(n-j+1)>0$, and $\mathrm{\Gamma }(2-q)>0$, implying that

$${\displaystyle \frac{\mathrm{\Gamma }(n-j-q)}{\mathrm{\Gamma }(n-j+1)\mathrm{\Gamma }(-q)}}>0,0\le j\le n-3,n\in {\mathbb{N}}_3;$$

(ii) 

For $q=2$, the numerical scheme (14) reduces to the IO form of Pell’s numbers (2).

Lemma 1.

Denote by

$$\underset{n\to \infty }{lim}{\displaystyle \frac{x(n+1)}{x\left(n\right)}}=\mathrm{\Lambda }.$$

(16)

Then, ${\displaystyle \mathrm{\Lambda }\le \frac{q+\sqrt{(4-q)(2+q)}}{2}}$.

Proof. 

Corresponding to (14), the numerical scheme is

$$\begin{array}{c}x(n+1)=qx\left(n\right)+\left[2-{\displaystyle \frac{q(q-1)}{2}}\right]x(n-1)\hfill \\ \hfill -\sum _{j=1}^{n-1}{\displaystyle \frac{\mathrm{\Gamma }(n-j-q+2)}{\mathrm{\Gamma }(n-j+3)\mathrm{\Gamma }(-q)}}x(j-1),n\in {\mathbb{N}}_1.\end{array}$$

(17)

Clearly,

$$\underset{n\to \infty }{lim}{\displaystyle \frac{x(n-1)}{x\left(n\right)}}={\displaystyle \frac{1}{\mathrm{\Lambda }}}.$$

(18)

From (17), we have

$$\begin{array}{c}{\displaystyle \frac{x(n+1)}{x\left(n\right)}}=q+\left[2-{\displaystyle \frac{q(q-1)}{2}}\right]{\displaystyle \frac{x(n-1)}{x\left(n\right)}}\hfill \\ \hfill -\sum _{j=1}^{n-1}{\displaystyle \frac{\mathrm{\Gamma }(n-j-q+2)}{\mathrm{\Gamma }(n-j+3)\mathrm{\Gamma }(-q)}}{\displaystyle \frac{x(j-1)}{x\left(n\right)}},n\in {\mathbb{N}}_1.\end{array}$$

(19)

For $n\in {\mathbb{N}}_1$ and $0\le j\le n-1$, consider

$${\displaystyle \frac{\mathrm{\Gamma }(n-j-q+2)}{\mathrm{\Gamma }(n-j+3)\mathrm{\Gamma }(-q)}}=q(q-1){\displaystyle \frac{\mathrm{\Gamma }(n-j-q+2)}{\mathrm{\Gamma }(n-j+3)\mathrm{\Gamma }(2-q)}}.$$

Clearly, by [7], $\mathrm{\Gamma }(n-j-q+2)>0$, $\mathrm{\Gamma }(n-j+3)>0$, and $\mathrm{\Gamma }(2-q)>0$, implying that

$${\displaystyle \frac{\mathrm{\Gamma }(n-j-q+2)}{\mathrm{\Gamma }(n-j+3)\mathrm{\Gamma }(-q)}}>0,0\le j\le n-1,n\in {\mathbb{N}}_1.$$

Also, $2-{\displaystyle \frac{q(q-1)}{2}}>0$, ${\displaystyle \frac{x(n-1)}{x\left(n\right)}}>0$, and

$${\displaystyle \frac{x(j-1)}{x\left(n\right)}}\ge 0,1\le j\le n-1,n\in {\mathbb{N}}_1.$$

Then, from (19), we have

$${\displaystyle \frac{x(n+1)}{x\left(n\right)}}\le q+\left[2-{\displaystyle \frac{q(q-1)}{2}}\right]{\displaystyle \frac{x(n-1)}{x\left(n\right)}},n\in {\mathbb{N}}_1.$$

(20)

Setting $n\to \infty$ on both sides of (20) and using (16) and (18), we obtain

$$\mathrm{\Lambda }\le q+\left[2-{\displaystyle \frac{q(q-1)}{2}}\right]{\displaystyle \frac{1}{\mathrm{\Lambda }}}.$$

(21)

Let us define A and B to simplify the inequality: $A=q$ and $B=\left[2-{\displaystyle \frac{q(q-1)}{2}}\right]$. Then, (21) is equivalent to

$${\mathrm{\Lambda }}^2-A\mathrm{\Lambda }-B\le 0.$$

(22)

Also, let

$${\lambda }_1={\displaystyle \frac{A+\sqrt{A^2+4B}}{2}},{\lambda }_2={\displaystyle \frac{A-\sqrt{A^2+4B}}{2}}.$$

Clearly, ${\lambda }_1>0$ and ${\lambda }_2<0$. Then, from (22), we obtain

$$\mathrm{\Lambda }\le {\lambda }_1.$$

That is,

$$\underset{n\to \infty }{lim}{\displaystyle \frac{x(n+1)}{x\left(n\right)}}\le {\displaystyle \frac{q+\sqrt{(4-q)(2+q)}}{2}}.$$

(23)

   □

If one denotes $E\left(q\right)={\displaystyle \frac{q+\sqrt{(4-q)(2+q)}}{2}}$, Figure 1 verifies the inequality ${\displaystyle \frac{x(n+1)}{x\left(n\right)}}<E\left(q\right)$ for $q=1.9$ and $n=1,2,\dots ,15$.

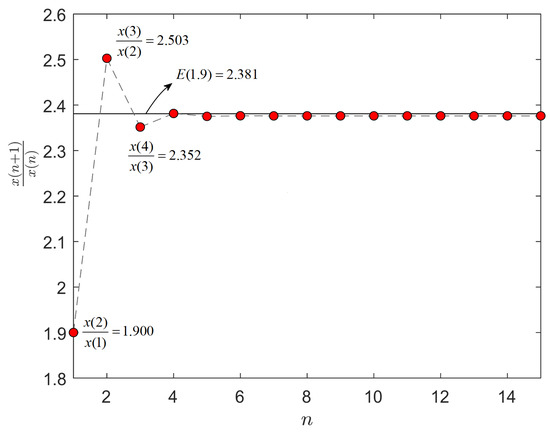
Figure 1. Numerical verification of the inequality (23) for $q=1.9$, $n=1,2,\dots ,15$. E represents the line ${\displaystyle \frac{2+\sqrt{(4-q)(2+q)}}{2}}$ in (23) for $q=1.9$.

Remark 3.

We now examine the special case when $q=2$. We have

$${\displaystyle \frac{\mathrm{\Gamma }(n-j-q+2)}{\mathrm{\Gamma }(n-j+3)\mathrm{\Gamma }(-q)}}=0,0\le j\le n-1,n\in {\mathbb{N}}_1.$$

Then, from (19), we have

$${\displaystyle \frac{x(n+1)}{x\left(n\right)}}=q+\left[2-{\displaystyle \frac{q(q-1)}{2}}\right]{\displaystyle \frac{x(n-1)}{x\left(n\right)}},n\in {\mathbb{N}}_1.$$

Consequently, we obtain

$$\mathrm{\Lambda }=\underset{n\to \infty }{lim}{\displaystyle \frac{P(n+1)}{P\left(n\right)}}={\lambda }_1={\displaystyle \frac{2+\sqrt{(4-2)(2+2)}}{2}}=1+\sqrt{2},$$

i.e., the known result for the integer order (IO) Pell’s numbers, $\delta =1+\sqrt{2}$ being the silver ratio.

3.4. Fractional Silver Ratio and Tiling Obtained with Fractional Pell’s Numbers

3.4.1. Fractional Silver Ratio

Definition 6

([23]). Let $v:{\mathbb{N}}_0\to \mathbb{R}$. The Z-transform of u is a complex function given by

$$\overline{u}\left(z\right)=Z\left[u\left(n\right)\right]=\sum _{k=0}^{\infty }u\left(k\right)z^{-k},$$

where z is a complex number for which this series converges absolutely.

Theorem 5.

The generalized characteristic equation for the fractional Pell sequence for $q\in (1,2)$ is given by

$$z^2{\left(1-{\displaystyle \frac{1}{z}}\right)}^q-2=0.$$

(24)

Proof. 

Denote by $Z\left[x\left(n\right)\right]=\overline{x}\left(z\right)$. Then,

$$Z\left[x(n+1)\right]=z\overline{x}\left(z\right)-zx\left(0\right),$$

and

$$Z\left[x(n+2)\right]=z^2\overline{x}\left(z\right)-z^{2}x\left(0\right)-zx\left(1\right).$$

Also, for $1<q<2$, by using Definitions 5 and 6, we have

$$\begin{array}{cc}\hfill Z\left[{\nabla }_0^{q}x\left(n\right)\right]& =\sum _{k=0}^{\infty }{\nabla }_0^{q}x\left(k\right)z^{-k}\hfill \\ & =\sum _{k=0}^{\infty }\left[\sum _{j=0}^k{\displaystyle \frac{\mathrm{\Gamma }(k-j-q)}{\mathrm{\Gamma }(k-j+1)\mathrm{\Gamma }(-q)}}x\left(j\right)\right]z^{-k}\hfill \\ & =\sum _{j=0}^{\infty }\left[\sum _{k=j}^{\infty }{\displaystyle \frac{\mathrm{\Gamma }(k-j-q)}{\mathrm{\Gamma }(k-j+1)\mathrm{\Gamma }(-q)}}{z}^{-k}\right]x\left(j\right)\hfill \\ & =\sum _{j=0}^{\infty }\left[\sum _{k=0}^{\infty }{\displaystyle \frac{\mathrm{\Gamma }(k-q)}{\mathrm{\Gamma }(k+1)\mathrm{\Gamma }(-q)}}{z}^{-k-j}\right]x\left(j\right)\hfill \\ & =\sum _{j=0}^{\infty }\left[\sum _{k=0}^{\infty }{\displaystyle \frac{\mathrm{\Gamma }(k-q)}{\mathrm{\Gamma }(k+1)\mathrm{\Gamma }(-q)}}{z}^{-k}\right]z^{-j}x\left(j\right)\hfill \\ & =\sum _{j=0}^{\infty }\left[{\left(1-{\displaystyle \frac{1}{z}}\right)}^q\right]z^{-j}x\left(j\right)\hfill \\ & ={\left(1-{\displaystyle \frac{1}{z}}\right)}^q\sum _{j=0}^{\infty }x\left(j\right)z^{-j}\hfill \\ & ={\left(1-{\displaystyle \frac{1}{z}}\right)}^q\overline{x}\left(z\right).\hfill \end{array}$$

Take

$$y\left(n\right)={\nabla }_0^{q}x\left(n\right)=\sum _{j=0}^n{\displaystyle \frac{\mathrm{\Gamma }(n-j-q)}{\mathrm{\Gamma }(n-j+1)\mathrm{\Gamma }(-q)}}x\left(j\right),n\in {\mathbb{N}}_0.$$

Then, $y\left(0\right)=x\left(0\right)=0$ and $y\left(1\right)=-qx\left(0\right)+x\left(1\right)=1$. Denote by $Z\left[y\left(n\right)\right]=\overline{y}\left(z\right)$. Then,

$$\begin{array}{cc}\hfill Z\left[{\nabla }_0^{q}x(n+2)\right]& =Z\left[y(n+2)\right]\hfill \\ & =z^2\overline{y}\left(z\right)-z^{2}y\left(0\right)-zy\left(1\right)\hfill \\ & =z^{2}Z\left[y\left(n\right)\right]-z\hfill \\ & =z^{2}Z\left[{\nabla }_0^{q}x\left(n\right)\right]-z\hfill \\ & =z^2{\left(1-{\displaystyle \frac{1}{z}}\right)}^q\overline{x}\left(z\right)-z.\hfill \end{array}$$

The equivalent form of the fractional Pell sequence is given by

$$\begin{array}{c}{\nabla }_0^{q}x(n+2)=2x\left(n\right),n\in {\mathbb{N}}_0.\end{array}$$

(25)

Taking the Z-transform of (25) and rearranging the terms, we get

$$z^2{\left(1-{\displaystyle \frac{1}{z}}\right)}^q\overline{x}\left(z\right)-z=2\overline{x}\left(z\right).$$

That is,

$$\overline{x}\left(z\right)={\displaystyle \frac{z}{z^2{\left(1-\frac{1}{z}\right)}^q-2}}.$$

Consequently, the fractional characteristic equation for the fractional Pell sequence is

$$z^2{\left(1-{\displaystyle \frac{1}{z}}\right)}^q-2=0.$$

   □

If one denotes with $\delta =\Re \left(z\right)$ the real part of z, then the characteristic equation becomes

$${\delta }^2{\left(1-{\displaystyle \frac{1}{\delta }}\right)}^q-2=0,$$

whose solutions are fractional silver ratio as function of q, $\delta =\delta \left(q\right)$.

For $q=1.5$, the generalized characteristic equation has the solution $\delta =2.2$; for $q=1.1$, one obtains $\delta =2.05$, while, for $q=2$, one obtains the characteristic equation of IO

$${\delta }^2-2\delta -1=0,$$

with the known silver ratio solution $\delta =1+\sqrt{2}$ (see also Remark 2 (ii)).

To determine the solutions graphically, denote the surface determined by the characteristic polynomial by $\mathrm{\Sigma }(\delta ,q):={\delta }^2{\left(1-{\displaystyle \frac{1}{\delta }}\right)}^q-2$, the surface $\overline{z}=\mathrm{\Sigma }(\delta ,q)$ being drawn in Figure 2. The intersection between $\mathrm{\Sigma }$ and the plane $\overline{z}=0$, denoted by $\mathrm{\Gamma }$ (red plot), represents the curve of solutions of the fractional characteristic equation. For example, for $q=1.5$, the numerical solution of the characteristic Equation (24) is $\delta =2.217$, which matches with the graphical solution; the intersection between the plane $q=1.5$ and $\mathrm{\Gamma }$ (point $P(2.217,1.5)$ in the plane $\overline{z}=0$).

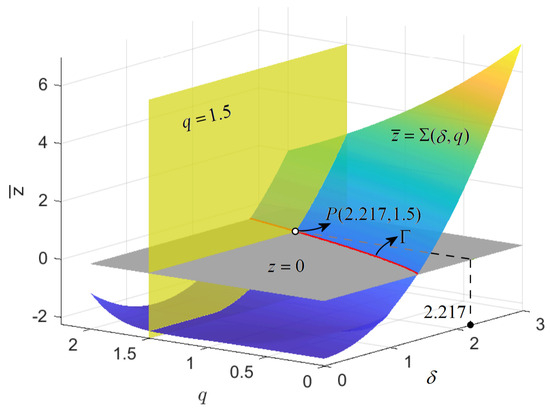
Figure 2. The curve $\mathrm{\Gamma }$ representing the solutions of the characteristic Equation (24) (red plot) as intersection between the plane $\overline{z}$ and the surface $\mathrm{\Sigma }$. For $q=1.5$, to obtain the solution of the characteristic equation, one crosses the curve $\mathrm{\Gamma }$ of the solution,with the plane $q=1.5$ and the point $P(2.217,1.5)$. The solution $\delta =2.217$ represents the fractional silver ratio for $q=1.5$.

3.4.2. Fractional Pell’s Tiling

As known, a domino tiling with Pell’s numbers is a tessellation of some region by dominoes by using rectangular tiles. For example, the kth rectangular tile has the length $P\left(k\right)$ and the width $2\times P(k-1)+P(k-2)$ (see, e.g., [24,25]). In Figure 3 the case of domino tiling with 8 Pell’s numbers is presented (the zoomed rectangle reveals the tiling steps).

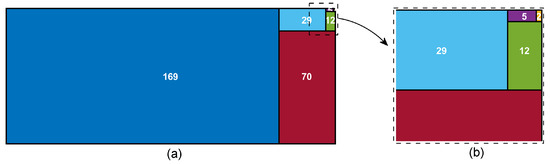
Figure 3. (a) Domino tiling with IOPell’s numbers; (b) zoomed detail reveals the construction of the tiling.

Also, the tiling can be generated with squares of Pell sequence lengths. To construct this tiling, start with the first square of size $1\times 1$, i.e., $P\left(1\right)$ ($P\left(0\right)$ is omitted, and then continue to the right with a square of size $2\times 2$, which means $P\left(2\right)$, then up with square of size $5\times 5$, i.e., $P\left(3\right)$, next left with a square of $12\times 12$, i.e., $P\left(5\right)$, down with a square $29\times 29$, i.e., $P\left(6\right)$, and so on, the rule being the rotation counterclockwise of each new rectangle, with 90 °C. Next, if one draws a quarter-circle arc inside each new square connecting opposite corners, one obtains the silver spiral (red plot in Figure 4a for a visual representation, where the IO case is considered).

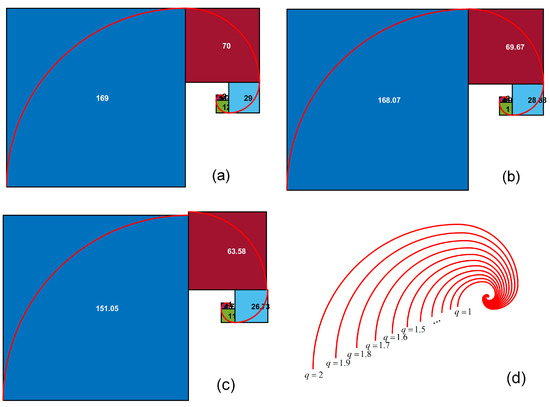
Figure 4. Silver spiral with 8 Pell numbers: (a) IO silver spiral; (b) fractional silver spiral for $q=1.995$; (c) fractional silver spiral for $q=1.9$; (d) fractional silver spiral for $q=1+10\times 0.1$ (for $q=2$, one obtains the IO silver spiral).

Considering now 8 fractional Pell’s numbers, the spiral and fractional silver spiral, plotted over the tiling for $q=1.995$ and $q=1.9$, are presented in Figure 4b and Figure 4c, respectively. For $q=1.995$, the fractional tiling and the fractional silver spiral are similar to the case of IO in Figure 4a; for $q=1.9$, the fitting differences become visible.

Figure 4d shows fractional silver spirals for $q=1+i\times 0.1$ for $i=0,\dots ,10$.

While in [11,12] it was shown that the fractional approach of discrete systems can break the symmetry, the fractional silver ratio introduced in this paper and also the fractional golden ratio (introduced in [10]) do not break the symmetry and the beauty of the perfection of nature. It is certainly known that the root mechanism that generates patterns in plants via the golden ratio, can be considered as an optimal packing, a fact first discovered by the German botanist Werner Hoffmeister in 19th century (see Figure 5). However, the fractional silver ratio generates artistic representations too. Thus, Figure 5 presents artistic representations of a pinecone using the MATLAB script presented in the appendix (the script can be found in [26]). The script, originally written to run with the golden ratio sequence as a factor of $\pi$ (see highlighted line 25), is easily adapted here to use the fractional silver ratio. In Figure 5a, the case of the IO silver ratio of IO is presented, in Figure 5b the case of fractional silver ratio $\delta =2.22$, corresponding to $q=1.5$, and in Figure 5c the case of the fractional silver ratio $\delta =2.05$, corresponding to $q=1.1$.

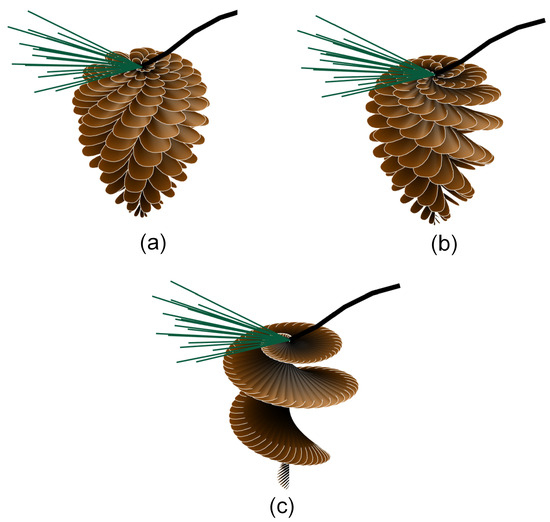
Figure 5. Artistic fractional pinecone obtained with the script [26] for (a) IO silver ratio, $\delta =1+\sqrt{2}$; (b) fractional silver ratio, $\delta =2.22$, corresponding to $q=1.5$; (c) fractional silver ratio, $\delta =2.05$, corresponding to $q=1.1$.

4. Fractional Pell–Lucas Sequence

A two-dimensional system of linear difference equations describing the Pell–Lucas sequence (4) is

$$\left(\begin{array}{c}Q(n+2)\\ Q(n+1)\end{array}\right)=\left(\begin{array}{cc}2& 1\\ 1& 0\end{array}\right)\left(\begin{array}{c}Q(n+1)\\ Q\left(n\right)\end{array}\right),n\in {\mathbb{N}}_0.$$

Then,

$$\left(\begin{array}{c}\nabla Q(n+2)\\ \nabla Q(n+1)\end{array}\right)=\left(\begin{array}{cc}1& 1\\ 1& -1\end{array}\right)\left(\begin{array}{c}Q(n+1)\\ Q\left(n\right)\end{array}\right),n\in {\mathbb{N}}_0.$$

Consequently, we have the following initial value problem

$$\begin{array}{c}\nabla \overline{Q}\left(n\right)=A\overline{Q}(n-1),n\in {\mathbb{N}}_1,\end{array}$$

(26)

$$\begin{array}{c}\overline{Q}\left(0\right)={\overline{Q}}_0,\end{array}$$

(27)

associated with the Pell–Lucas numbers. Here,

$$\begin{array}{cc}\hfill \overline{Q}\left(n\right)& =\left(\begin{array}{c}Q(n+1)\\ Q\left(n\right)\end{array}\right),\hfill \\ \hfill A& =\left(\begin{array}{cc}1& 1\\ 1& -1\end{array}\right),\hfill \\ \hfill {\overline{Q}}_0& =\left(\begin{array}{c}Q\left(1\right)\\ Q\left(0\right)\end{array}\right)=\left(\begin{array}{c}2\\ 2\end{array}\right).\hfill \end{array}$$

We observe that the matrix A in (26) is same as in (5). Now, for $0<q<1$, we consider the $q^{\mathrm{th}}$-order difference equation

$${\nabla }_0^q\overline{y}\left(n\right)=A\overline{y}(n-1),n\in {\mathbb{N}}_1,$$

together with the initial condition

$$\overline{y}\left(0\right)=\left(\begin{array}{c}2\\ 2\end{array}\right),$$

analogous to (26) and (27). Here,

$$\overline{y}\left(n\right)=\left(\begin{array}{c}y(n+1)\\ y\left(n\right)\end{array}\right),A=\left(\begin{array}{cc}1& 1\\ 1& -1\end{array}\right).$$

4.1. Closed Form of the Fractional Pell–Lucas Sequence

With the help of Theorem 1, we mimic the proof of Theorem 2 to obtain the following statement, the generalized Binet’s formula for fractional Pell–Lucas sequence.

Theorem 6.

The closed-form expression of the fractional Pell–Lucas sequence is given by

$$y\left(n\right)=\sum _{k=0}^n\left[{\phi }^k+{\left(-\phi \right)}^k\right]{\displaystyle \frac{\mathrm{\Gamma }(n-k+kq+q)}{\mathrm{\Gamma }(n-k+1)\mathrm{\Gamma }(kq+q)}},n\in {\mathbb{N}}_0.$$

Remark 4.

For $q=1$, we obtain the closed IO form expression for the nth element in Pell–Lucas sequences (3) and (4) as follows:

$$\begin{array}{cc}\hfill y\left(n\right)& ={\displaystyle \frac{1}{\phi }}\sum _{k=0}^n\left[{\phi }^k+{\left(-\phi \right)}^k\right]{\displaystyle \frac{\mathrm{\Gamma }(n+1)}{\mathrm{\Gamma }(n-k+1)\mathrm{\Gamma }(k+1)}}\hfill \\ \hfill & =\sum _{k=0}^n\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right){\phi }^k+\sum _{k=0}^n\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right){\left(-\phi \right)}^k\hfill \\ \hfill & ={\left(1+\phi \right)}^n+{\left(1-\phi \right)}^n\hfill \\ \hfill & ={\left(1+\sqrt{2}\right)}^n+{\left(1-\sqrt{2}\right)}^n,\hfill \end{array}$$

for $n\in {\mathbb{N}}_0$.

Theorem 7.

$y\left(n\right)>0$ for all $n\in {\mathbb{N}}_0$.

Proof. 

The proof is similar to the proof of Theorem 3. So, we omit it.    □

4.2. Numerical Scheme for the Fractional Pell–Lucas Sequence

Following the steps from the start of Section 3.3 and by considering (4) instead of (2), the numerical integral for the fractional Pell–Lucas sequence can be obtained.

Using Definition 3, (4) can be rewritten as

$${\nabla }^{2}Q\left(n\right)=f\left(Q(n-1),Q(n-2)\right),n\in {\mathbb{N}}_2,$$

(28)

where

$$f\left(Q(n-1),Q(n-2)\right)=2Q(n-2),n\in {\mathbb{N}}_2.$$

Now, for $1<q<2$, we consider the $q^{\mathrm{th}}$-order difference equation

$${\nabla }_0^{q}y\left(n\right)=f\left(y(n-1),y(n-2)\right),n\in {\mathbb{N}}_2,$$

together with the initial condition

$$y\left(0\right)=2,y\left(1\right)=2,$$

analogous to (3)–(28).

Theorem 8.

The numerical scheme for the fractional Pell–Lucas sequence is given by

$$\begin{array}{c}y\left(n\right)=qy(n-1)+\left[2-{\displaystyle \frac{q(q-1)}{2}}\right]y(n-2)\hfill \\ \hfill -\sum _{j=0}^{n-3}{\displaystyle \frac{\mathrm{\Gamma }(n-j-q)}{\mathrm{\Gamma }(n-j+1)\mathrm{\Gamma }(-q)}}y\left(j\right),n\in {\mathbb{N}}_2.\end{array}$$

(29)

Proof. 

The proof is similar to the proof of Theorem 4. So, we omit it.    □

Remark 5.

For $q=2$, the numerical scheme (29) reduces to the IO definition of the Pell–Lucas numbers.

For example, the first 15 fractional Pell–Lucas numbers displayed with 4 decimals for $q=1.999$ are

$$\begin{array}{c}2,2,6.0099,13.9999,33.9940,81.9739,197.9108,477.72047,1153.17036,2783.6227,\hfill \\ \hfill 6719.3551,16219.7623,39152.61760,94509.48860,228129.71839.\end{array}$$

By mimicking the proof of Lemma 1, we obtain the following statement:

Lemma 2.

${\displaystyle \underset{n\to \infty }{lim}\frac{y(n+1)}{y\left(n\right)}\le \frac{q+\sqrt{(4-q)(2+q)}}{2}}$.

Remark 6.

Similar to Remark 3, for $q=2$, we obtain

$$\underset{n\to \infty }{lim}{\displaystyle \frac{Q(n+1)}{Q\left(n\right)}}=1+\sqrt{2}.$$

Theorem 9.

The characteristic equation for the fractional Pell–Lucas sequence is given by (24).

Proof. 

The proof is similar to the proof of Theorem 5. So, we omit it.    □

5. Conclusions

In this paper, the fractional generalization of Pell and Pell–Lucas numbers is introduced by considering the Grünwald–Letnikov fractional operator of orders $q\in (0,1)$ and $q\in (1,2)$. Several properties of integer-order Pell and Pell–Lucas numbers extend naturally to the fractional case.The fractional silver ratio is deduced from the characteristic equation of the fractional Pell numbers as a function of the fractional order q. The numerical tests show that the fractional Pell numbers can be used to tile a region, and the fractional silver spiral fits the tiling, demonstrating that the fractional silver spiral aligns well with the fractional tiling pattern. This work, which continues the study in [10], offers a new perspective on the use of fractional calculus in recurrence-defined numbers.