Pore Structure and Multifractal Characteristics of the Upper Lianggaoshan Formation in the Northeastern Sichuan Basin, China
Abstract
1. Introduction
2. Geological Background
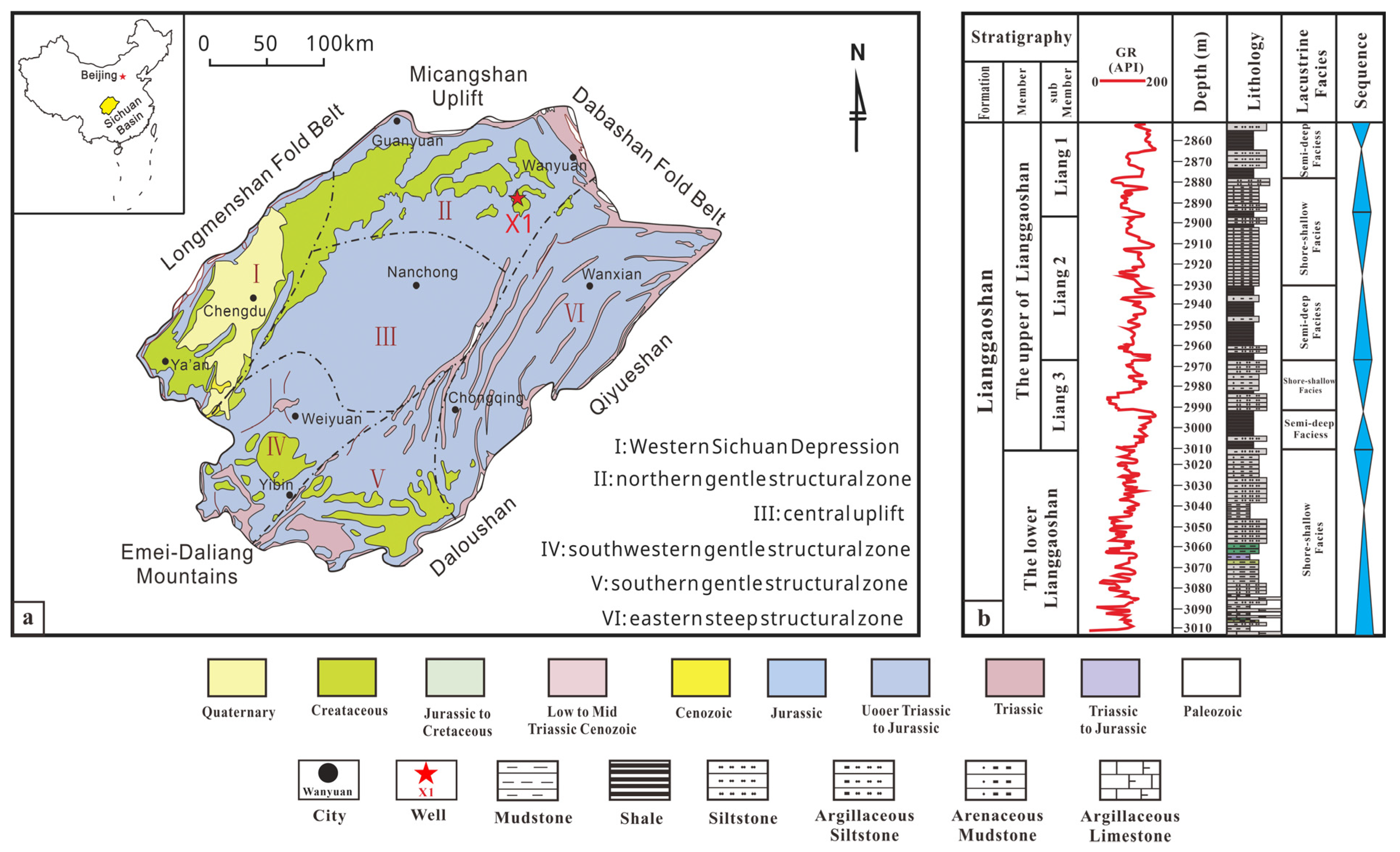
3. Methods
3.1. Experimental Samples
3.2. Gas Adsorption Experiments
3.3. HPMI
3.4. NMR
3.5. Single-Exponent Fractal Analysis Based on LTNA and HPMI
3.6. Multifractal Analysis Based on NMR
4. Results and Discussions
4.1. Pore Structure Characteristics
4.1.1. Pore Structure Characteristics Based on LTCA
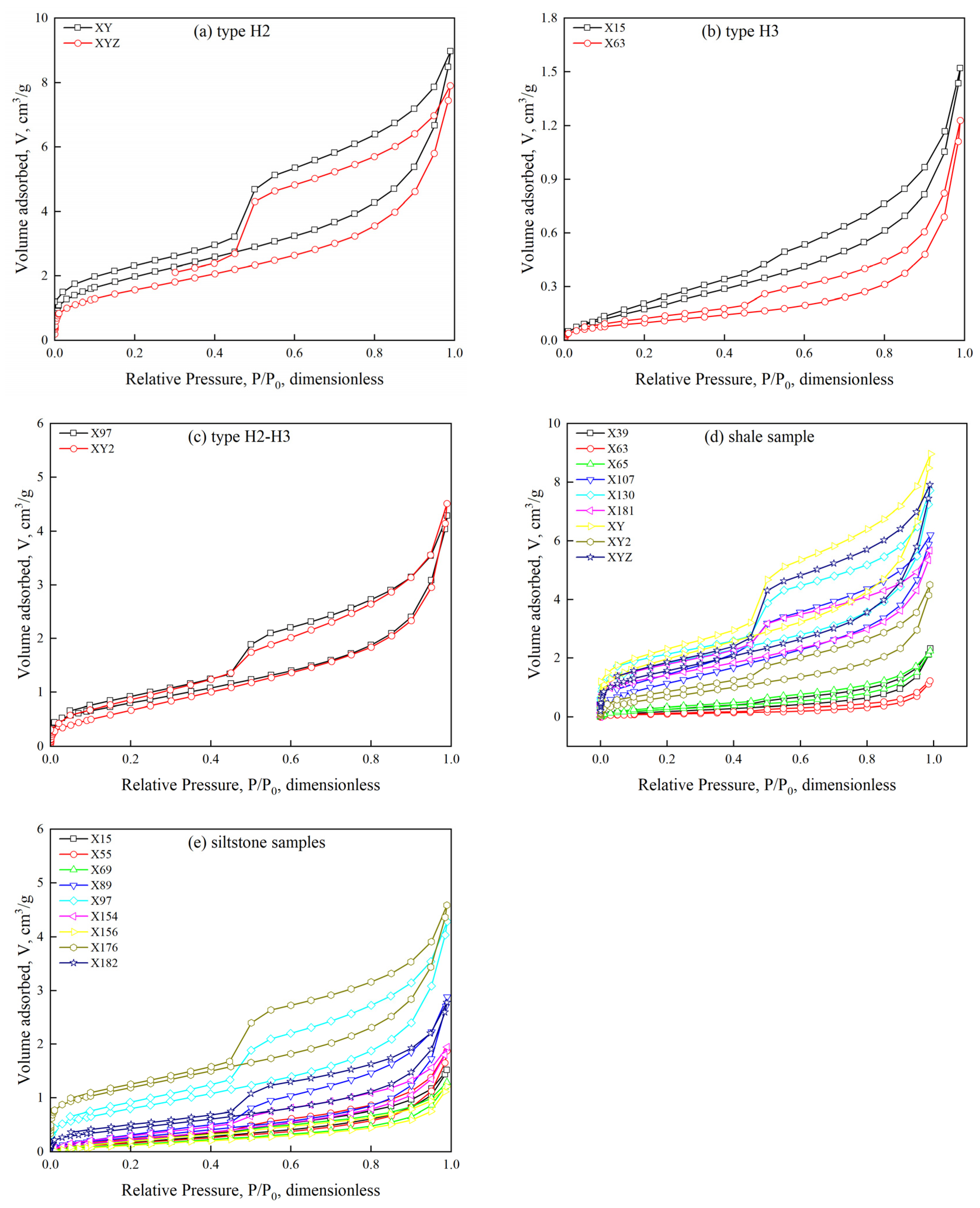
4.1.2. Pore Structure Characteristics Based on LTNA
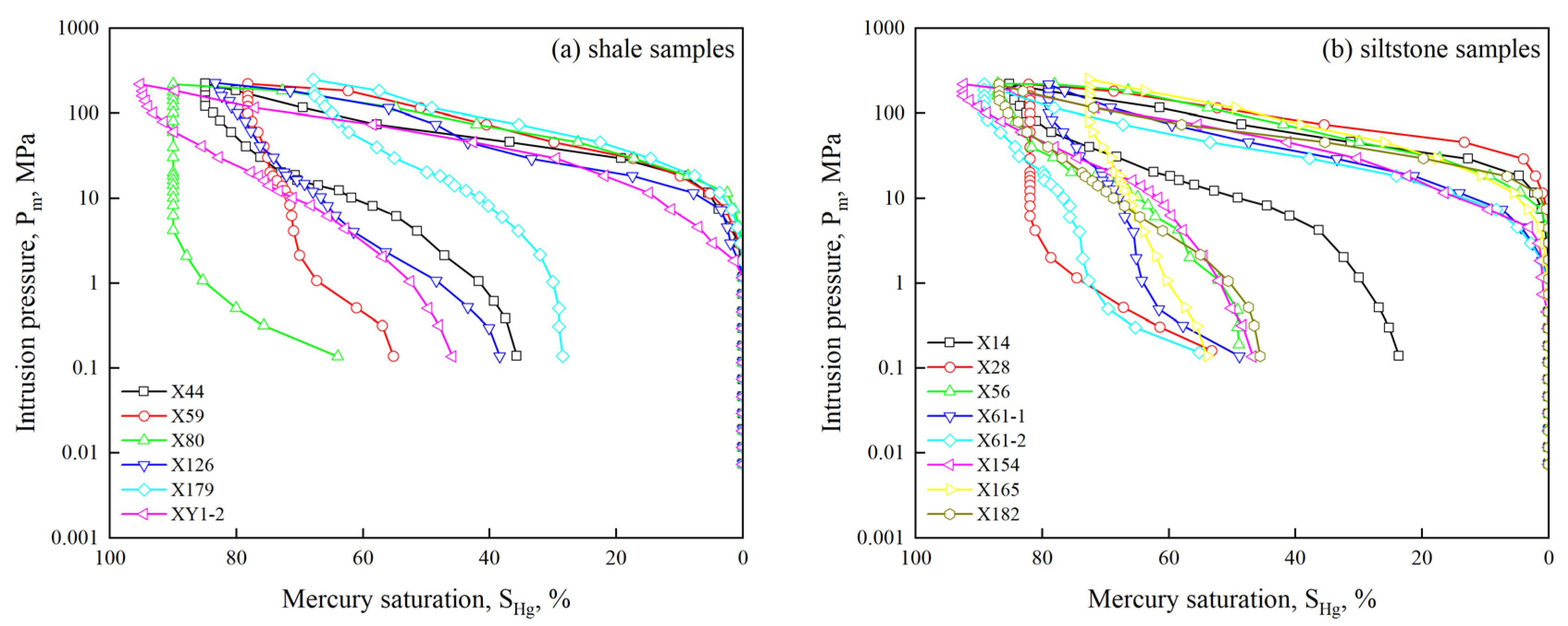
4.1.3. Pore Structure Characteristics Based on HPMI
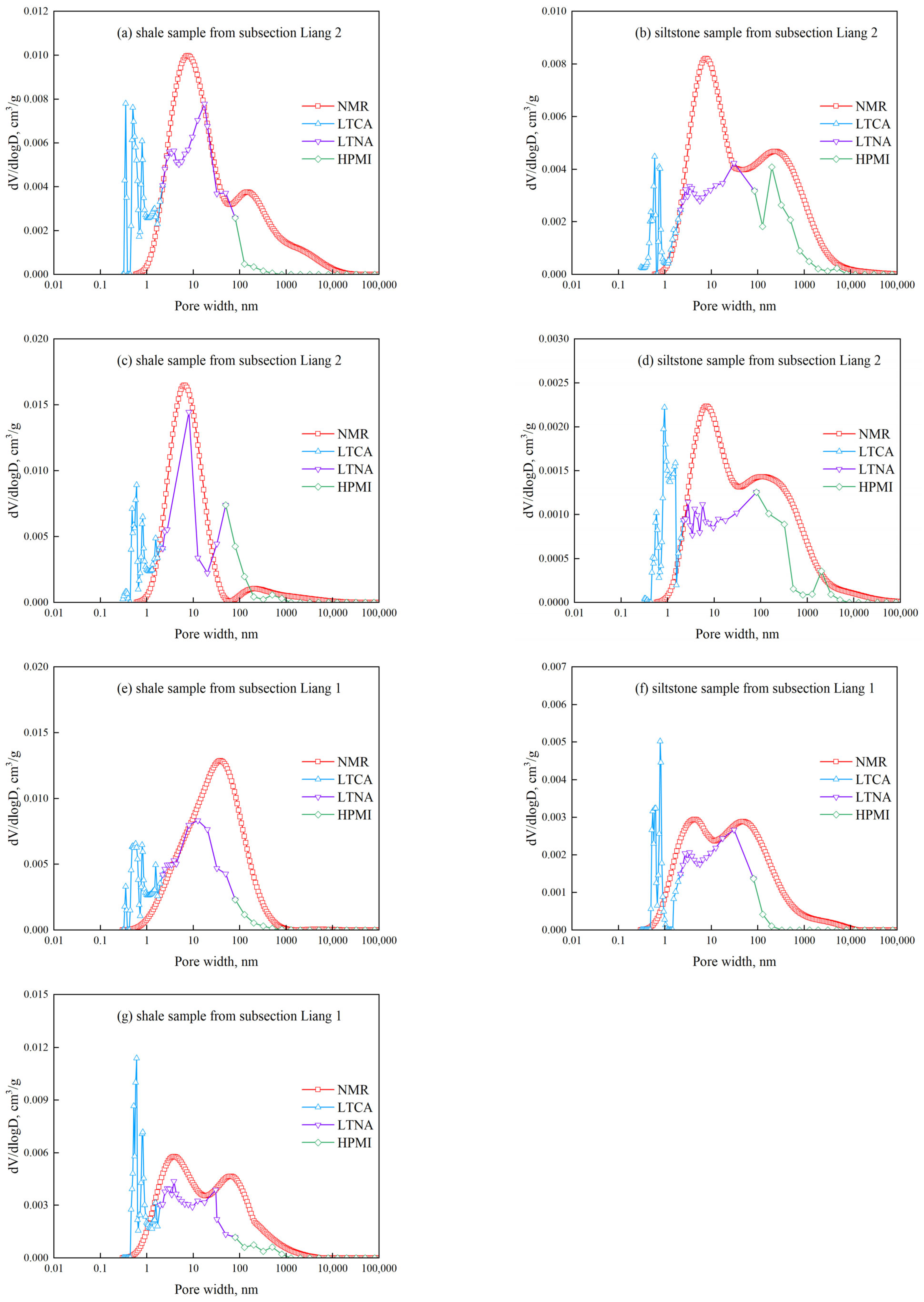
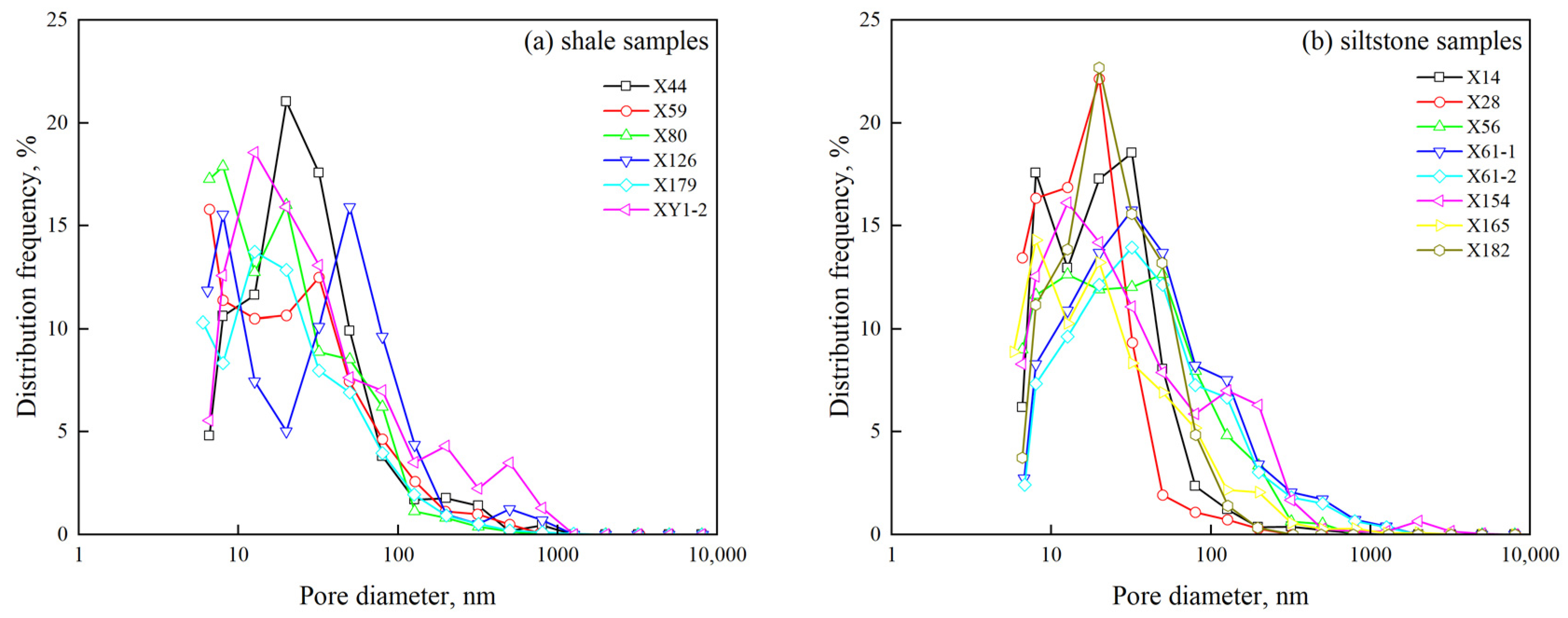
4.1.4. Pore Structure Characteristics Based on NMR
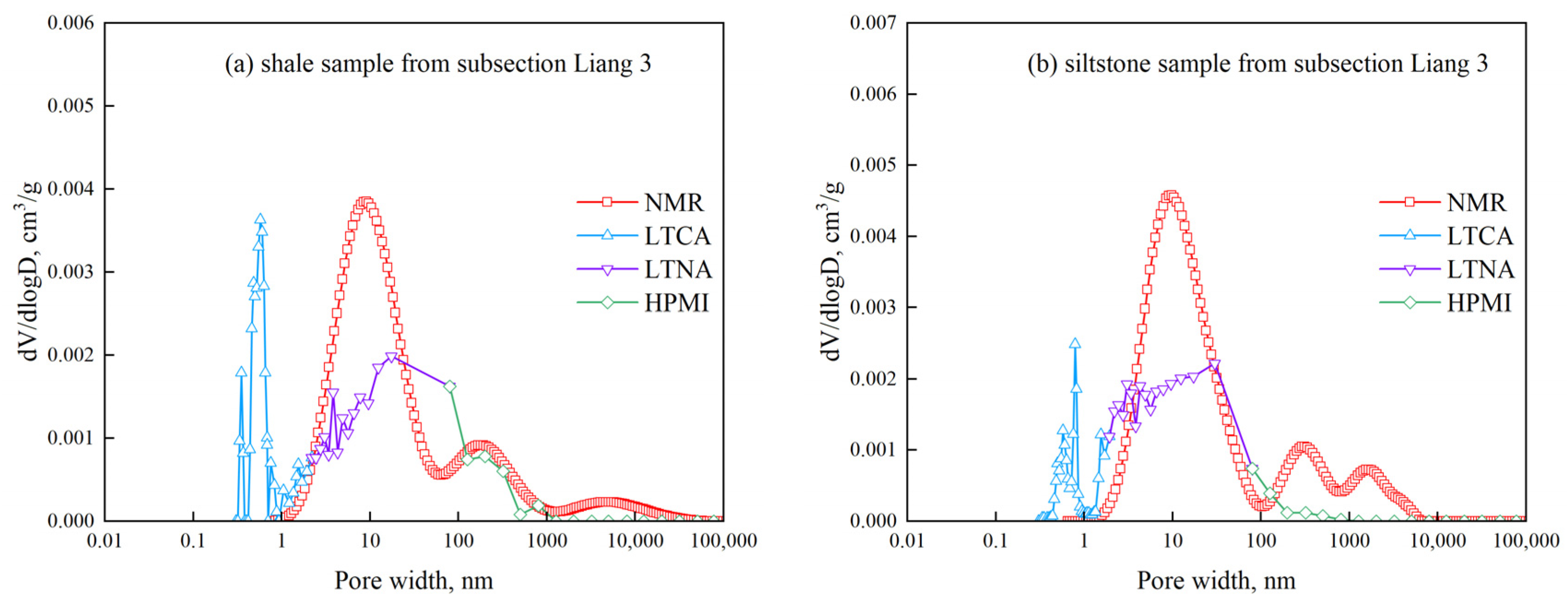
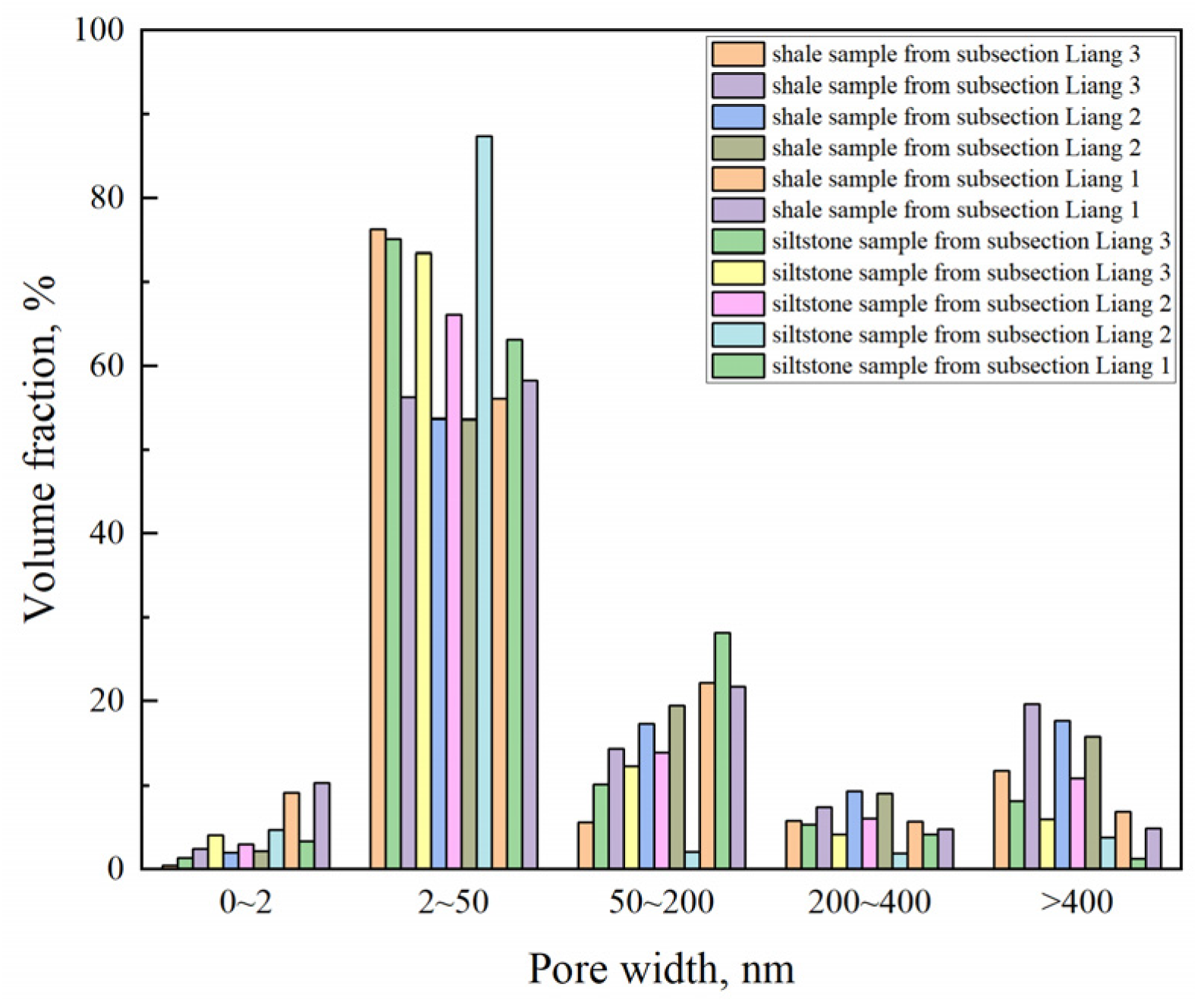
4.2. Characterization of Full-Scale Pore Size Distribution
4.3. Fractal Characteristics of Full-Scale Pores
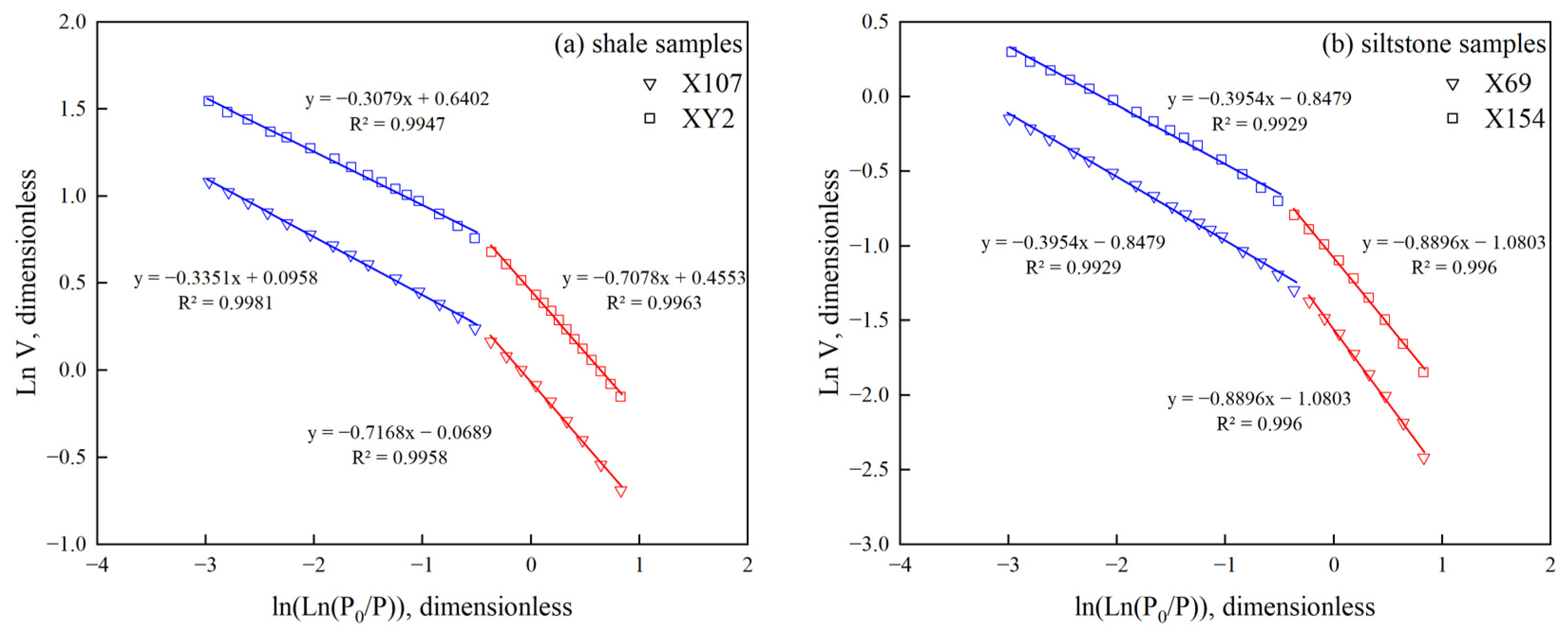
4.3.1. Fractal Dimensions Obtained by LTNA
4.3.2. Fractal Dimension Obtained by HPMI Curves
4.3.3. Multifractal Dimensions Obtained by NMR Curves
4.3.4. Fractal Characteristics of Multi-Scale Pore Structure and Fluid Diffusion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BJH | Barrette–Joyner–Halenda |
| BET | Brunauer–Emmett–Teller |
| CPMG | Carr-Purcell-Meiboom-Gill |
| FHH | Frenkel–Halsey–Hill |
| HPMI | high-pressure mercury intrusion |
| IUPAC | International Union of Pure and Applied Chemistry |
| LGS | Lianggaoshan |
| LTCA | low-pressure CO2 adsorption |
| LTNA | low-temperature N2 adsorption |
| NMR | nuclear magnetic resonance |
| NK | Neimark–Kiselev |
| PV | Pore Volume |
| PSD | pore size distribution |
| SSA | Specific Surface Area |
Appendix A
References
- Liu, G.; Liu, R.; Du, J.; Zhang, K.; Yu, J.; Liu, Q. Study on Pore Structure and Fractal Characterization during Thermal Evolution of Oil Shale Experiments. ACS Omega 2022, 7, 12922–12936. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Dong, X.; Zhang, J.; Chen, H.; Zhang, W. A 3D FIB-SEM technique for quantitative characterization of oil shale’s microstructure: A case study from the Shahejie Formation in Dongying Depression, China. Energy Sci. Eng. 2021, 9, 116–128. [Google Scholar] [CrossRef]
- He, W.; Meng, Q.; Feng, Z.; Zhang, J.; Wang, R. In-situ accumulation theory and exploration & development practice ofGulong shale oil in Songliao Basin. Acta Pet. Sin. 2022, 43, 1–14. [Google Scholar] [CrossRef]
- Lu, F.; Zhou, Y.; Wang, P.; Jia, K.; Han, G. Pore Characteristics of Oil Shales in Jilin Province, Northeast China: Investigations Using Gas Adsorption, Mercury Intrusion, and NMR Cryoporometry. Energy Fuels 2023, 37, 11914–11927. [Google Scholar] [CrossRef]
- Zhang, P.; Yin, Y.; Lu, S.; Li, J.; Chang, X.; Zhang, J.; Pang, Y.; Chen, G.; Liu, Y.; Li, Z. Insights into Pore Structures and Multifractal Characteristics of Shale Oil Reservoirs: A Case Study from Dongying Sag, Bohai Bay Basin, China. Energy Fuels 2022, 36, 8224–8237. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Solano, N.; Bustin, R.M.; Bustin, A.M.M.; Chalmers, G.R.L.; He, L.; Melnichenko, Y.B.; Radlinski, A.P.; Blach, T.P. Pore structure characterization of North American shale gas reservoirs using USANS/SANS, gas adsorption, and mercury intrusion. Fuel 2013, 103, 606–616. [Google Scholar] [CrossRef]
- Liu, X.; Xiong, J.; Liang, L. Investigation of pore structure and fractal characteristics of organic-rich Yanchang formation shale in central China by nitrogen adsorption/desorption analysis. J. Nat. Gas Sci. Eng. 2015, 22, 62–72. [Google Scholar] [CrossRef]
- Yan, J.; He, X.; Geng, B.; Hu, Q.; Feng, C.; Kou, X.; Li, X. Nuclear magnetic resonance T2 spectrum: Multifractal characteristics and pore structure evaluation. Appl. Geophys. 2017, 14, 205–215. [Google Scholar] [CrossRef]
- Hong, H.; Lu, J.; Qin, C.; Zhang, S.; Zhang, R.; Zhou, Y.; Xiao, Z.; Xiao, H.; Han, L. Shale oil reservoir characteristics and exploration implication in Da’anzhai Member of Jurassic Ziliujing Formation in central Sichuan Basin. Pet. Geol. Exp. 2024, 46, 11–21. [Google Scholar] [CrossRef]
- Wang, Z.; Fu, X.; Hao, M.; Li, G.; Pan, J.; Niu, Q.; Zhou, H. Experimental insights into the adsorption-desorption of CH4/N2 and induced strain for medium-rank coals. J. Pet. Sci. Eng. 2021, 204, 108705. [Google Scholar] [CrossRef]
- Lei, J.; Pan, B.; Guo, Y.; Fan, Y.; Xue, L.; Deng, S.; Zhang, L.; Ruhan, A. A comprehensive analysis of the pyrolysis effects on oil shale pore structures at multiscale using different measurement methods. Energy 2021, 227, 120359. [Google Scholar] [CrossRef]
- Maria, M.; Agnieszka, D.; Arndt, S. Porosity of Devonian and Mississippian New Albany Shale across a maturation gradient: Insights from organic petrology, gas adsorption, and mercury intrusion. AAPG Bull. 2013, 97, 1621–1643. [Google Scholar] [CrossRef]
- Lu, Z.; Liu, C.; Zang, Q.; Wu, Y.; Yang, X.; Yang, H.; Zeng, X.; Li, W. Analysis of the pore structure of tight sandstone by high-pressure mercury injection combined with fractal theory: A case study of the Heshui area in the Ordos Basin. Bull. Geol. Sci. Technol. 2023, 42, 264–273. [Google Scholar] [CrossRef]
- Yang, R.; He, S.; Yi, J.; Hu, Q. Nano-scale pore structure and fractal dimension of organic-rich Wufeng-Longmaxi shale from Jiaoshiba area, Sichuan Basin: Investigations using FE-SEM, gas adsorption and helium pycnometry. Mar. Pet. Geol. 2016, 70, 27–45. [Google Scholar] [CrossRef]
- Rui, Y.; Wang, C.; Zhang, F.; Yao, Y.; Guo, N.; Zheng, R. Characterization of micro-pore throats in the shale gas reservoirs of Zhaotong National Shale Gas Demonstration Area. Nat. Gas Ind. 2021, 41, 78–85. [Google Scholar]
- Zhao, Y.; Sun, Y.; Liu, S.; Wang, K.; Jiang, Y. Pore structure characterization of coal by NMR cryoporometry. Fuel 2017, 190, 359–369. [Google Scholar] [CrossRef]
- Zhang, P.; Lu, S.; Li, J. Characterization of pore size distributions of shale oil reservoirs: A case study from Dongying sag, Bohai Bay basin, China. Mar. Pet. Geol. 2019, 100, 297–308. [Google Scholar] [CrossRef]
- Jin, J.; Liu, W.; Wang, Z.; Guo, H.; Li, Q.; Li, Z.; Bai, N.; Liu, J. Quantitative Characterization of Shale Pore Size Distribution Based on Nuclear Magnetic Resonance T2 Spectrum. Sci. Technol. Eng. 2022, 22, 6448–6455. [Google Scholar]
- Chang, J.; Fan, X.; Jiang, Z.; Wang, X.; Chen, Z. Differential impact of clay minerals and organic matter on pore structure and its fractal characteristics of marine and continental shales in China. Appl. Clay Sci. 2022, 216, 106334. [Google Scholar] [CrossRef]
- Ma, B.; Hu, Q.; Yang, S.; Zhang, T.; Qiao, H.; Meng, M.; Zhu, X.; Sun, X. Pore structure typing and fractal characteristics of lacustrine shale from Kongdian Formation in East China. J. Nat. Gas Sci. Eng. 2020, 85, 103709. [Google Scholar] [CrossRef]
- Zhang, Q.; Liang, F.; Liang, P.; Zhou, S.; Guo, W.; Guo, W.; Lu, B.; Liu, W. Investigation of fractal characteristics and its main controlling factors of shalereservoir: A case study of the Longmaxi shale in Weiyuan shale gas field. J. China Univ. Min. Technol. 2020, 49, 110–122. [Google Scholar] [CrossRef]
- Yang, F.; Ning, Z.; Wang, Q.; Kong, D.; Peng, K.; Xiao, L. Fractal characteristics of nanopore in shales. Nat. Gas Geosci. 2014, 25, 618–623. [Google Scholar] [CrossRef]
- Ji, W.; Song, Y.; Jiang, Z.; Meng, M.; Liu, Q.; Chen, L.; Wang, P.; Gao, F.; Huang, H. Fractal characteristics of nano-pores in the Lower Silurian Longmaxi shales from the Upper Yangtze Platform, south China. Mar. Pet. Geol. 2016, 78, 88–98. [Google Scholar] [CrossRef]
- Tang, L.; Song, Y.; Jiang, Z.; Jiang, S.; Li, Q. Pore Structure and Fractal Characteristics of Distinct Thermally Mature Shales. Energy Fuels 2019, 33, 5116–5128. [Google Scholar] [CrossRef]
- Hu, D.; Li, Z.; Wei, Z.; Duan, J.; Miao, Z.; Pan, L.; Li, C.; Duan, H. Major advancement in oil and gas exploration of Jurassic channel sandstone in Well Bazhong 1HF in northern Sichuan Basin and its significance. Nat. Gas Ind. B 2023, 10, 270–282. [Google Scholar] [CrossRef]
- Wang, X.; Wang, M.; Zhao, C.; Yang, X.; Jia, Y.; Wu, R.; Li, T.; Zhao, X.; Tang, Y. Reservoir characteristics and controlling factors of the middle–high maturity multiple lithofacies reservoirs of the Lianggaoshan Formation shale strata in the northeastern Sichuan basin, China. Mar. Pet. Geol. 2024, 161, 106692. [Google Scholar] [CrossRef]
- He, W.; He, H.; Wang, Y.; Cui, B.; Meng, Q.; Guo, X.; Bai, X.; Wang, Y. Major breakthrough and significance of shale oil of the Jurassic Lianggaoshan Formation in Well Ping’an 1 in northeastern Sichuan Basin. China Pet. Explor. 2022, 27, 40–49. [Google Scholar] [CrossRef]
- Li, J.; Tao, S.; Wang, Z.; Zou, C.; Gao, X.; Wang, S. Characteristics of Jurassic Petroleum Geology and Main Factors of Hydrocarbon Accumulation in NE Sichuan Basin. Nat. Gas Geosci. 2010, 21, 732–741. [Google Scholar]
- Yang, Y.; Yang, J.; Yang, G.; Tao, S.; Ni, C.; Zhang, B.; He, X.; Lin, J.; Huang, D.; Liu, M.; et al. New research progress of Jurassie tight oil in central Sichuan Basin. Pet. Explor. Dev. 2016, 43, 873–882. [Google Scholar] [CrossRef]
- Chen, S.; Gao, X.; Wang, L.; Lu, J.; Liu, C.; Tang, H.; Zhang, H.X.; Huang, Y.; Ni, S. Factors controlling oiliness of Jurassic Lianggaoshan tight sands in central Sichuan Basin, SW China. J. Pet. Explor. Dev. 2014, 41, 421–427. [Google Scholar] [CrossRef]
- Chen, M.; Wang, L.; He, J.; Tan, J.; Hong, H.; Zhao, D.; Kong, L.; Cai, C.; Tan, Y. Application of rock pyrolysis experiment in oil-bearing property evaluation of shale oil reservoir: A case study of the Jurassic Lianggaoshan Formation in the northeastern Sichuan Basin. China Pet. Explor. 2024, 29, 166–176. [Google Scholar] [CrossRef]
- Wang, Y.; Mao, C.; Duan, X. Coupling of Paleosedimentary Environment and Lithofacies: Implications for Shale Oil Enrichment in the Lianggaoshan Formation, Northeastern Sichuan Basin, China. ACS Omega 2024, 9, 28237–28252. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Passoja, D.E.; Paullay, A.J. Fractal character of fracture surfaces of metals. Nature 1984, 308, 721–722. [Google Scholar] [CrossRef]
- Zhang, Z.; Weller, A. Fractal dimension of pore-space geometry of an Eocene sandstone formation. Geophysics 2014, 79, 377–387. [Google Scholar] [CrossRef]
- Lai, J.; Wang, G.; Wang, Z.; Chen, J.; Pang, X.; Wang, S.; Zhou, Z.; He, Z.; Qin, Z.; Fan, X. A review on pore structure characterization in tight sandstones. Earth Sci. Rev. 2018, 177, 436–457. [Google Scholar] [CrossRef]
- Huang, J.; Dong, D.; Li, J.; Hu, J.; Wang, Y. Reservoir fractal characteristics of continental shale: An example from Triassic Xujiahe Formation shale, Sichuan Basin, China. Nat. Gas Geosci. 2016, 27, 1611–1618. [Google Scholar] [CrossRef]
- Pratiksha, D.K.; Lalit, K.K.; Nandi, S. Characterization of heterogeneous petroleum reservoir of Indian Sub-continent: An integrated approach of hydraulic flow unit—Mercury intrusion capillary pressure—Fractal model. J. Pet. Sci. Eng. 2021, 205, 108788. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Lin, W.; Ma, L.; Liu, D.; Liu, J.; Zhang, Y. Micro-pore structure and fractal characteristics of deep shale from Wufeng Formation to Longmaxi Formation in Jingmen exploration area, Hubei Province, China. J. Nat. Gas Geosci. 2022, 7, 121–132. [Google Scholar] [CrossRef]
- Zhao, H.; Guo, Y.; Du, X.; Hu, Y.; Kang, R.; Shangguan, J.W. Micro-pore multifractal characteristics of Benxi Formation sandstone reservoir in Gaogiao area, Ordos Basin. Bull. Geol. Sci. Technol. 2020, 39, 175–184. [Google Scholar] [CrossRef]
- Peng, Y.; Du, Y.; Jiang, L.; Fang, Z.; Chao, J.; Yang, Y.; Sun, N.; Cao, Z. Micropore structure and fractal characteristics of shale oil reservoir in gentle slope zone of jiyang Depression. Fault-Block Oil Gas Field 2023, 30, 535–544. [Google Scholar]
- Zhao, D.; Guo, Y.; Xie, D.; Su, C.; Yang, Y.; Yu, Y. Fractal characteristics of shale reservoir pores based on low-temperature nitrogen adsorption experiments. J. Northeast Pet. Univ. 2014, 38, 100–108. [Google Scholar] [CrossRef]
- Bu, H.; Ju, Y.; Tan, J.; Wang, G.; Li, X. Fractal characteristics of pores in non-marine shales from the Huainan coalfield, eastern China. J. Nat. Gas Sci. Eng. 2015, 24, 166–177. [Google Scholar] [CrossRef]
- Wang, J. Fine Characterization of Shale Reservoir of Taiyuan and Shanxi Formations in Yulin Area, Ordos Basin. Ph.D. Thesis, China University of Geosciences, Beijing, China, 2021. [Google Scholar]
- Li, P.; Zheng, M.; Bi, H.; Wu, S.; Wang, X. Pore throat structure and fractal characteristics of tight oil sandstone: A case study in the Ordos Basin, China. J. Pet. Sci. Eng. 2017, 149, 665–674. [Google Scholar] [CrossRef]
- Wang, F.; Zai, Y. Fractal and multifractal characteristics of shale nanopores. Results Phys. 2021, 25, 104277. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, C.; Ouyang, S.; Luo, B.; Zhao, D.; Sun, W.; Awan, R.S.; Lu, Z.; Li, G.; Zang, Q. Investigation of pore-throat structure and fractal characteristics of tight sandstones using HPMI, CRMI, and NMR methods: A case study of the lower Shihezi Formation in the Sulige area, Ordos Basin. J. Pet. Sci. Eng. 2022, 210, 110053. [Google Scholar] [CrossRef]
- Wang, X.; Qi, M.; Hu, Y.; Qiu, Y. Analysis Of The Shale Pore Structures By The Combination Of High-Pressure Mercury Injection and Fractal Theory. Pet. Geol. Oilfield Dev. Daqin 2015, 34, 165–169. [Google Scholar] [CrossRef]
- Gouyet, J.-F.; Bug, A.L.R. Physics and Fractal Structures. Am. J. Phys. 1997, 65, 676. [Google Scholar] [CrossRef]
- Maslov, N.; Haris, K.; Latha, G.; Chakraborty, B. Multifractal Approach for Seafloor Characterization. IEEE Geosci. Remote Sens. Lett. 2014, 11, 54–58. [Google Scholar] [CrossRef]
- Ge, X.; Xiao, Y.; Fan, Y.; Liu, J.; Zhang, Y. Laboratory investigation of the relationship between static rock elastic parameters and low field nuclear magnetic resonance data. Int. J. Rock Mech. Min. Sci. 2020, 127, 104207. [Google Scholar] [CrossRef]
- Yang, X.; Wang, M.; Bai, X.; Wang, X.; Ying, Y.; Li, T.; Dong, J.; Huang, S.; Chen, J. Reservoir Space Characteristics and Exploration of Shale Oil Mobility of the Jurassic Lianggaoshan Formation Shale in the northeasten Sichuan Basin. Petroleum. Science. Bulletin. 2024, 9, 196–212. [Google Scholar] [CrossRef]
- Wu, J. Study on Pore Structure and Wettability of Shale Reservoir in Lianggaosahn Formation in Eastern Sichuan. Master’s Thesis, Yangtze University, Jingzhou, China, 2023. [Google Scholar]
- Yu, H.; Yang, R.; He, Z.; Bao, H.; Han, Y.; Zhang, W.; Xiong, S.; Wang, F.; Hu, Q.; He, S. Full-Scale Pore Structure and Fractal Characteristics of Continental Organic-Rich Shale: A Case Study of the Dongyuemiao Member of Jurassic Ziliujing Formation in the Fuxing Area, Eastern Sichuan Basin. Energy Fuels 2023, 37, 10426–10443. [Google Scholar] [CrossRef]
- Xiao, L.; Li, Z.; Yang, Y.; Tang, L.; Liang, Z.; Yu, H.; Hou, Y.; Wang, L. Pore structure and fractal characteristics of different lithofacies shales of the Lower Silurian Longmaxi Formation in southeast Chongqing. Sci. Technol. Eng. 2021, 21, 512–521. [Google Scholar]
- Rajyaguru, A.; Metzler, R.; Cherstvy, A.G.; Berkowitz, B. Quantifying anomalous chemical diffusion through disordered porous rock materials. Phys. Chem. Chem. Phys. PCCP 2025, 27, 9056–9067. [Google Scholar] [CrossRef] [PubMed]
- Fomin, S.A.; Chugunov, V.A.; Hashida, T. Non-Fickian mass transport in fractured porous media. Adv. Water Resour. 2011, 34, 205–214. [Google Scholar] [CrossRef]
- Li, Y. Fractal Characteristics of Multi-Scale Porestructure and Gas Diffusion in Tectonic Coal. Ph.D. Thesis, Henan Polytechnic University, Jiaozuo, China, 2019. [Google Scholar]





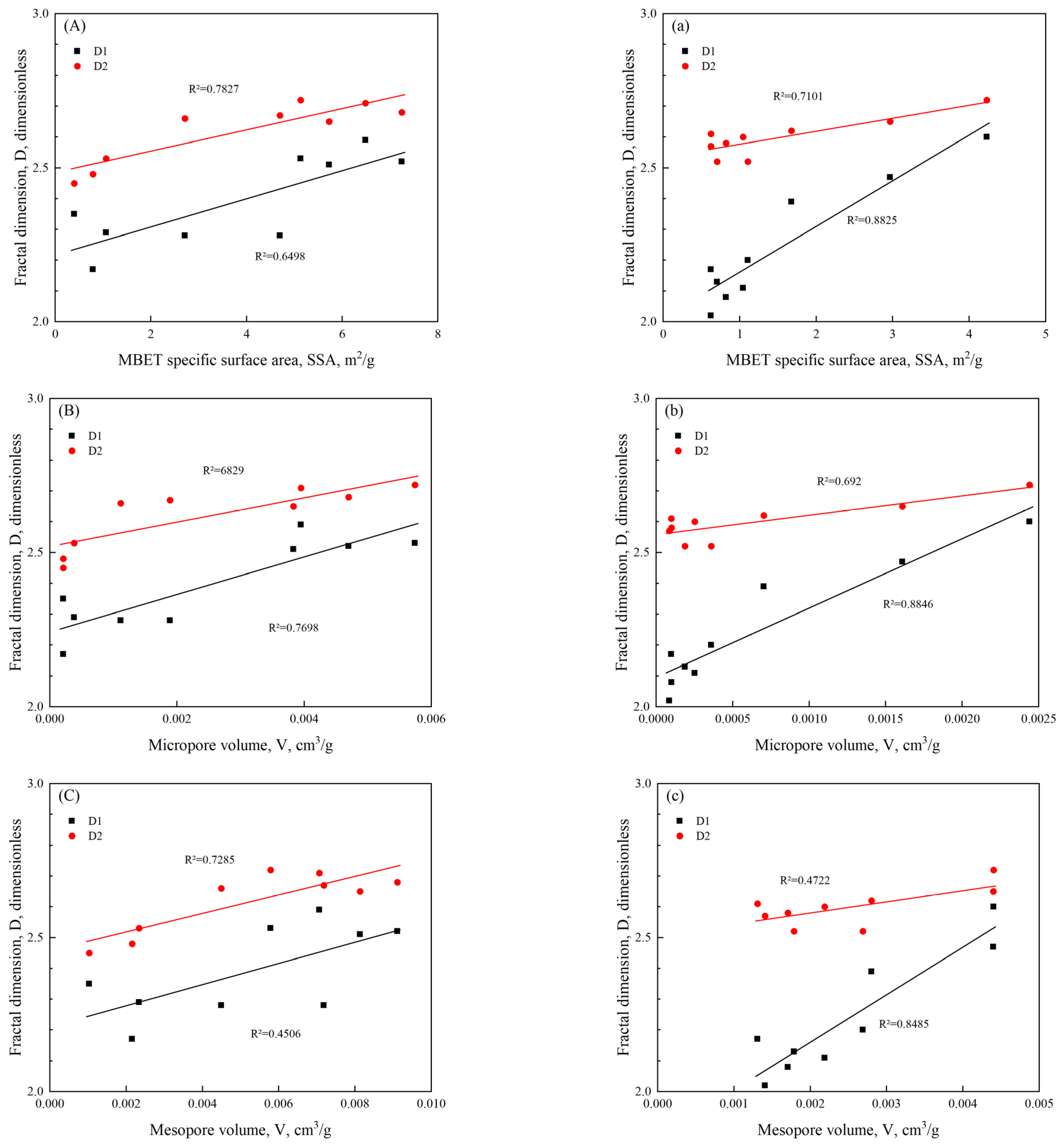
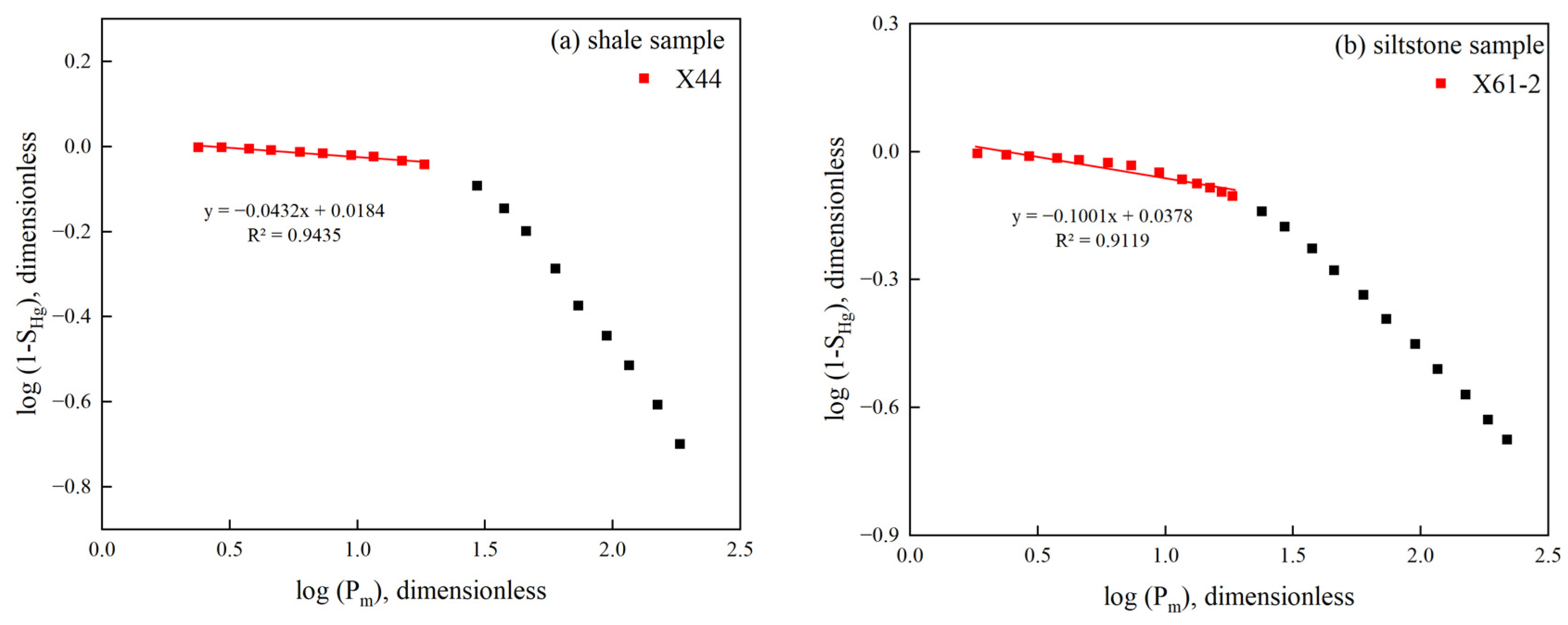

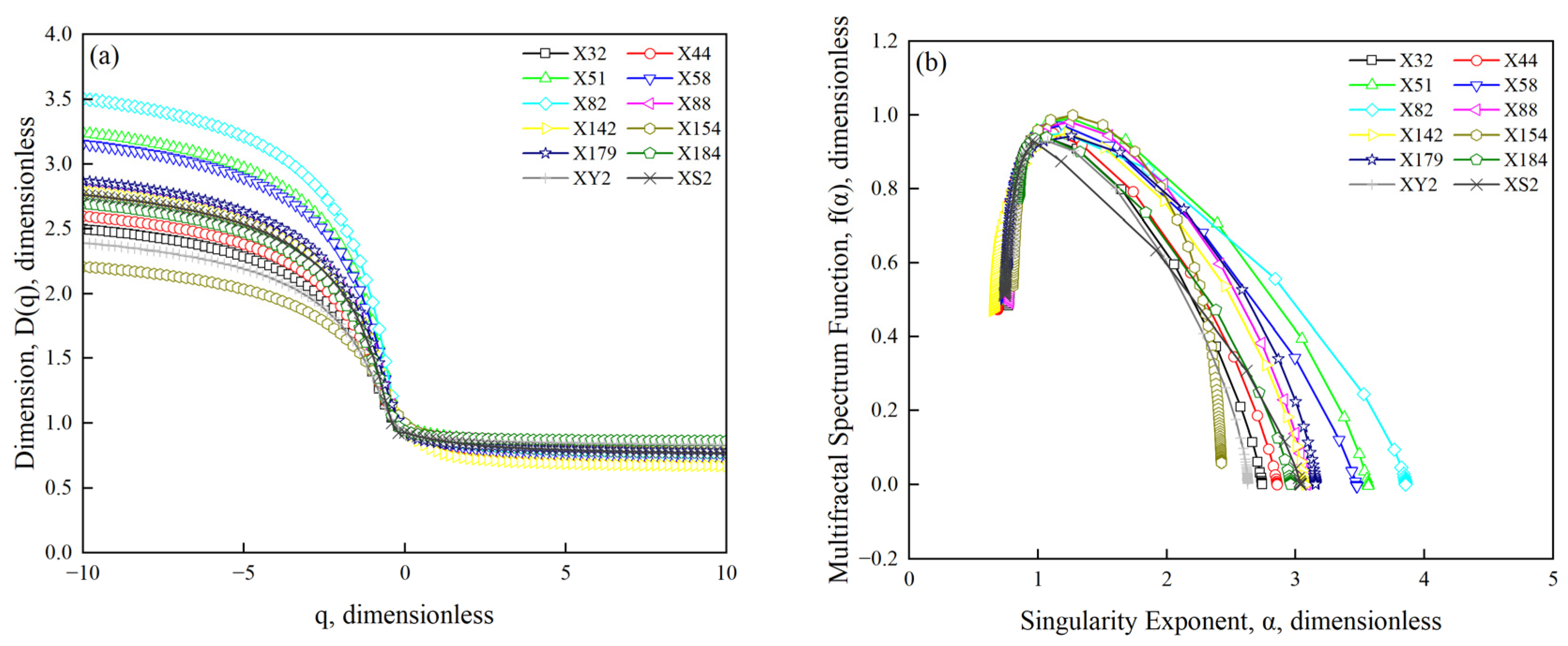

| Sample ID | Stratum | Depth (m) | Maximum Adsorption Capacity (cm3/g) | SSA (m2/g) | PV (cm3/g) |
|---|---|---|---|---|---|
| X15 | Liang 3 | 3012.81 | 1.519 | 0.823 | 0.003 |
| X39 | Liang 3 | 3025.85 | 2.317 | 0.791 | 0.004 |
| X55 | Liang 3 | 3035.80 | 1.879 | 0.706 | 0.003 |
| X63 | Liang 3 | 3046.14 | 1.228 | 0.396 | 0.002 |
| X65 | Liang 3 | 3046.94 | 2.245 | 1.061 | 0.003 |
| X69 | Liang 3 | 3047.99 | 1.290 | 0.626 | 0.002 |
| X89 | Liang 2 | 3065.43 | 2.884 | 1.106 | 0.004 |
| X97 | Liang 2 | 3069.41 | 4.287 | 2.965 | 0.007 |
| X107 | Liang 2 | 3075.98 | 6.206 | 4.701 | 0.010 |
| X130 | Liang 2 | 3089.73 | 7.717 | 6.487 | 0.012 |
| X154 | Liang 2 | 3104.61 | 1.945 | 1.046 | 0.003 |
| X156 | Liang 2 | 3106.62 | 1.215 | 0.625 | 0.002 |
| X176 | Liang 1 | 3119.21 | 4.584 | 4.231 | 0.007 |
| X181 | Liang 1 | 3123.91 | 5.671 | 5.129 | 0.009 |
| X182 | Liang 1 | 3124.06 | 2.775 | 1.678 | 0.005 |
| XY | Liang 1 | 3142.20 | 8.966 | 7.247 | 0.014 |
| XY2 | Liang 1 | 3142.70 | 4.510 | 2.714 | 0.007 |
| XYZ | Liang 1 | 3143.20 | 7.902 | 5.726 | 0.012 |
| Sample ID | Median Pore Radius (nm) | Threshold Pressure (MPa) | Median Pressure (MPa) | Sorting Coefficient | Mean Coefficient | Average Pore Radius (nm) |
|---|---|---|---|---|---|---|
| X14 | 9.400 | 23.888 | 78.591 | 1.130 | 15.681 | 8.800 |
| X28 | 6.700 | 37.553 | 110.215 | 0.930 | 16.097 | 7.100 |
| X44 | 11.600 | 23.968 | 63.291 | 1.290 | 15.347 | 10.500 |
| X56 | 11.300 | 9.509 | 64.760 | 1.470 | 15.247 | 10.000 |
| X59 | 6.600 | 14.940 | 111.998 | 1.430 | 15.635 | 7.900 |
| X61-1 | 14.200 | 9.499 | 51.894 | 1.570 | 14.750 | 13.700 |
| X61-2 | 17.400 | 9.509 | 42.212 | 1.540 | 14.748 | 13.200 |
| X80 | 7.300 | 14.979 | 100.071 | 1.270 | 15.852 | 7.400 |
| X126 | 9.000 | 14.985 | 82.072 | 1.620 | 15.262 | 9.100 |
| X154 | 11.700 | 5.975 | 62.901 | 1.720 | 15.126 | 10.100 |
| X165 | 6.200 | 15.081 | 118.659 | 1.500 | 15.575 | 8.300 |
| X179 | 5.800 | 24.079 | 127.253 | 1.360 | 15.665 | 8.200 |
| X182 | 11.500 | 14.850 | 63.738 | 1.050 | 15.463 | 10.500 |
| XY1-2 | 12.500 | 3.770 | 58.869 | 1.730 | 15.075 | 10.600 |
| Sample ID | Subsection | Depth (m) | Lithology | D1 | R2 | D2 | R2 |
|---|---|---|---|---|---|---|---|
| X15 | Liang 3 | 3012.81 | siltstone | 2.08 | 0.9954 | 2.58 | 0.9915 |
| X39 | Liang 3 | 3025.85 | shale | 2.17 | 0.9954 | 2.48 | 0.9995 |
| X55 | Liang 3 | 3035.80 | siltstone | 2.13 | 0.9979 | 2.52 | 0.9975 |
| X63 | Liang 3 | 3046.14 | shale | 2.35 | 0.9992 | 2.45 | 0.9998 |
| X65 | Liang 3 | 3046.94 | shale | 2.29 | 0.9983 | 2.53 | 0.9967 |
| X69 | Liang 3 | 3047.99 | siltstone | 2.02 | 0.9946 | 2.57 | 0.9949 |
| X89 | Liang 2 | 3065.43 | siltstone | 2.20 | 0.9969 | 2.52 | 0.9997 |
| X97 | Liang 2 | 3069.41 | siltstone | 2.47 | 0.9997 | 2.65 | 0.9991 |
| X107 | Liang 2 | 3075.98 | shale | 2.28 | 0.9978 | 2.67 | 0.9912 |
| X130 | Liang 2 | 3089.73 | shale | 2.59 | 0.9998 | 2.71 | 0.9999 |
| X154 | Liang 2 | 3104.61 | siltstone | 2.11 | 0.996 | 2.60 | 0.992 |
| X156 | Liang 2 | 3106.62 | siltstone | 2.17 | 0.9931 | 2.61 | 0.9937 |
| X176 | Liang 1 | 3119.21 | siltstone | 2.60 | 0.9998 | 2.72 | 0.9997 |
| X181 | Liang 1 | 3123.91 | siltstone | 2.39 | 0.9992 | 2.62 | 0.999 |
| X182 | Liang 1 | 3124.06 | shale | 2.53 | 0.9998 | 2.72 | 0.9946 |
| XY | Liang 1 | 3142.20 | shale | 2.52 | 0.9988 | 2.68 | 0.9987 |
| XY2 | Liang 1 | 3142.70 | shale | 2.28 | 0.9958 | 2.66 | 0.9975 |
| XYZ | Liang 1 | 3143.20 | shale | 2.51 | 0.9992 | 2.65 | 0.9995 |
| Sample ID | Subsection | D3 | R2 | Median Pore Radius (nm) | Average Pore Radius (nm) |
|---|---|---|---|---|---|
| X14 | Liang 3 | 2.9889 | 0.8936 | 9.4 | 8.8 |
| X28 | Liang 3 | 2.9763 | 0.968 | 6.7 | 7.1 |
| X44 | Liang 3 | 2.9619 | 0.9637 | 11.6 | 10.5 |
| X56 | Liang 3 | 2.9156 | 0.9015 | 11.3 | 10.0 |
| X59 | Liang 3 | 2.9722 | 0.9157 | 6.6 | 7.9 |
| X61-1 | Liang 3 | 2.9203 | 0.857 | 14.2 | 13.7 |
| X61-2 | Liang 3 | 2.906 | 0.9119 | 17.4 | 13.2 |
| X80 | Liang 2 | 2.9828 | 0.9604 | 7.3 | 7.4 |
| X126 | Liang 2 | 2.9733 | 0.921 | 9.0 | 9.1 |
| X154 | Liang 2 | 2.9438 | 0.7343 | 11.7 | 10.1 |
| X165 | Liang 2 | 2.9946 | 0.9029 | 6.2 | 8.3 |
| X179 | Liang 1 | 2.9909 | 0.8688 | 5.8 | 8.2 |
| X182 | Liang 1 | 2.9314 | 0.9064 | 11.5 | 10.5 |
| XY1-2 | Liang 1 | 2.9053 | 0.9623 | 12.5 | 10.6 |
| Sample ID | − | − | ||||||
|---|---|---|---|---|---|---|---|---|
| X32 | 2.494 | 0.802 | 0.936 | 0.887 | 0.868 | 0.135 | 1.557 | 1.692 |
| X44 | 2.596 | 0.712 | 0.951 | 0.850 | 0.792 | 0.239 | 1.645 | 1.884 |
| X51 | 3.241 | 0.801 | 0.992 | 0.906 | 0.878 | 0.191 | 2.249 | 2.440 |
| X58 | 3.158 | 0.737 | 0.972 | 0.862 | 0.812 | 0.236 | 2.186 | 2.421 |
| X82 | 3.504 | 0.774 | 0.951 | 0.883 | 0.848 | 0.177 | 2.553 | 2.730 |
| X88 | 2.807 | 0.816 | 0.982 | 0.894 | 0.877 | 0.167 | 1.824 | 1.991 |
| X142 | 2.795 | 0.668 | 0.951 | 0.782 | 0.727 | 0.283 | 1.844 | 2.127 |
| X154 | 2.209 | 0.837 | 1.000 | 0.903 | 0.886 | 0.163 | 1.209 | 1.372 |
| X179 | 2.869 | 0.781 | 0.944 | 0.849 | 0.827 | 0.163 | 1.925 | 2.089 |
| X184 | 2.693 | 0.861 | 0.940 | 0.897 | 0.883 | 0.079 | 1.753 | 1.832 |
| XY2 | 2.390 | 0.831 | 0.930 | 0.884 | 0.871 | 0.098 | 1.460 | 1.559 |
| XS2 | 2.762 | 0.768 | 0.930 | 0.869 | 0.838 | 0.162 | 1.832 | 1.994 |
| Sample ID | αmin | αmax | α0 | Δα |
|---|---|---|---|---|
| X32 | 0.770 | 2.743 | 1.091 | 1.973 |
| X44 | 0.688 | 2.856 | 1.118 | 2.168 |
| X51 | 0.771 | 3.566 | 1.256 | 2.795 |
| X58 | 0.714 | 3.475 | 1.190 | 2.762 |
| X82 | 0.750 | 3.854 | 1.208 | 3.104 |
| X88 | 0.783 | 3.087 | 1.251 | 2.304 |
| X142 | 0.648 | 3.074 | 1.230 | 2.426 |
| X154 | 0.807 | 2.424 | 1.271 | 1.617 |
| X179 | 0.760 | 3.156 | 1.262 | 2.396 |
| X184 | 0.853 | 2.963 | 1.065 | 2.110 |
| XY2 | 0.810 | 2.629 | 1.078 | 1.819 |
| XS2 | 0.742 | 3.038 | 0.976 | 2.296 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Luo, G.; Wang, H.; Zhang, L. Pore Structure and Multifractal Characteristics of the Upper Lianggaoshan Formation in the Northeastern Sichuan Basin, China. Fractal Fract. 2025, 9, 430. https://doi.org/10.3390/fractalfract9070430
Guo J, Luo G, Wang H, Zhang L. Pore Structure and Multifractal Characteristics of the Upper Lianggaoshan Formation in the Northeastern Sichuan Basin, China. Fractal and Fractional. 2025; 9(7):430. https://doi.org/10.3390/fractalfract9070430
Chicago/Turabian StyleGuo, Jingjing, Guotao Luo, Haitao Wang, and Liehui Zhang. 2025. "Pore Structure and Multifractal Characteristics of the Upper Lianggaoshan Formation in the Northeastern Sichuan Basin, China" Fractal and Fractional 9, no. 7: 430. https://doi.org/10.3390/fractalfract9070430
APA StyleGuo, J., Luo, G., Wang, H., & Zhang, L. (2025). Pore Structure and Multifractal Characteristics of the Upper Lianggaoshan Formation in the Northeastern Sichuan Basin, China. Fractal and Fractional, 9(7), 430. https://doi.org/10.3390/fractalfract9070430





