Heterogeneity of Deep Tight Sandstone Reservoirs Using Fractal and Multifractal Analysis Based on Well Logs and Its Correlation with Gas Production
Abstract
1. Introduction
2. Geological Setting

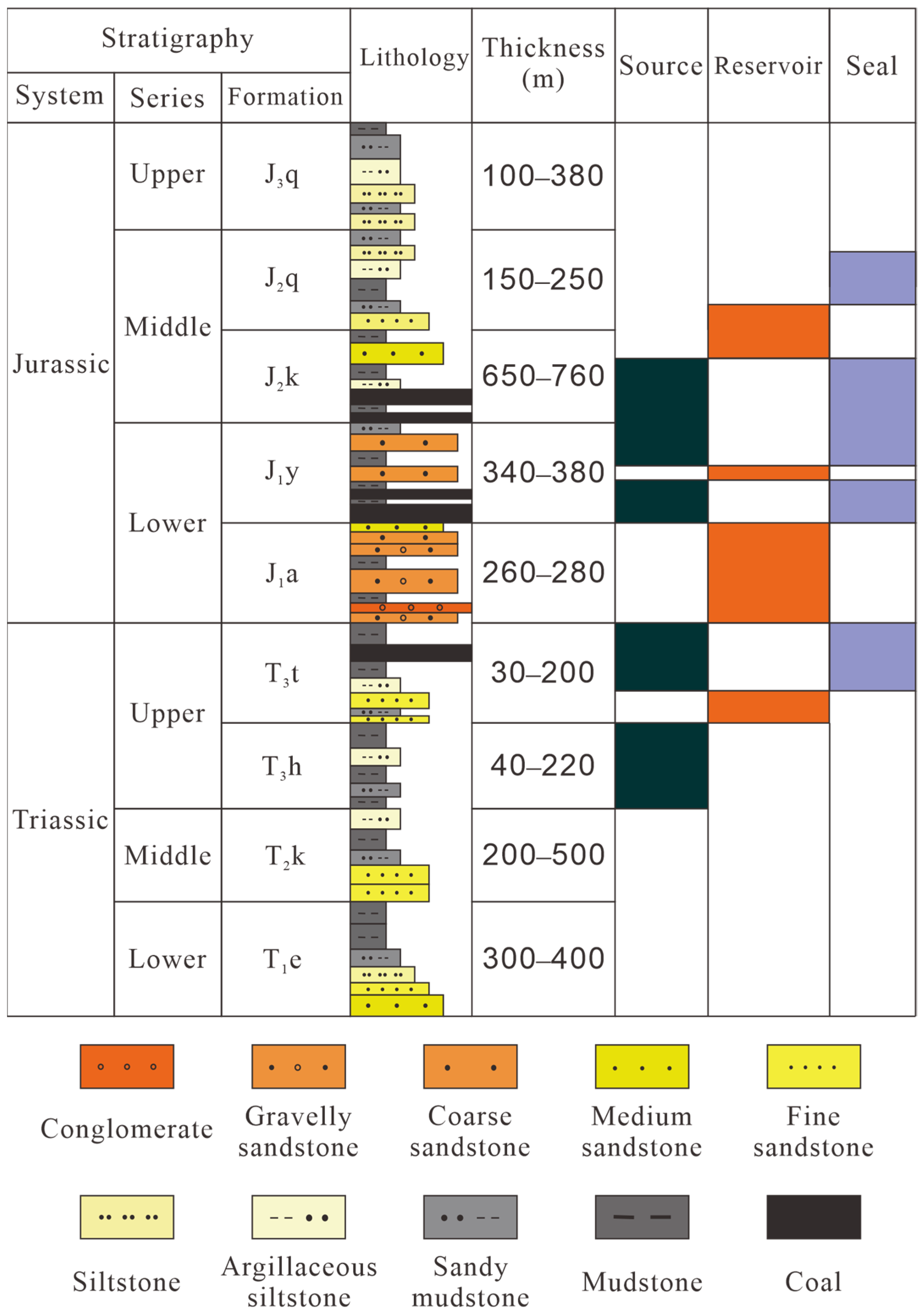
3. Calculation of Heterogeneity
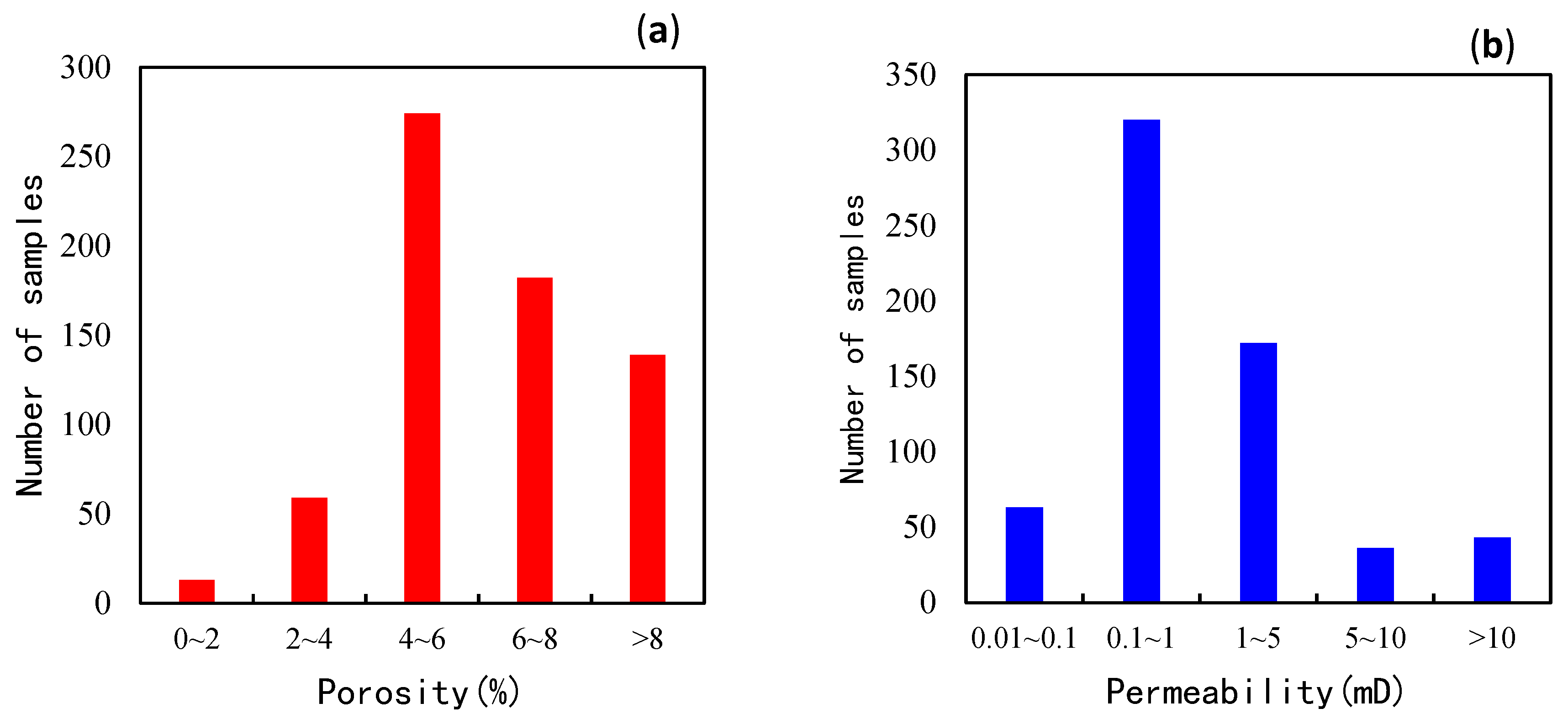
3.1. Heterogeneity Based on Core Permeability
3.2. Methods for Calculating Fractal Dimensions
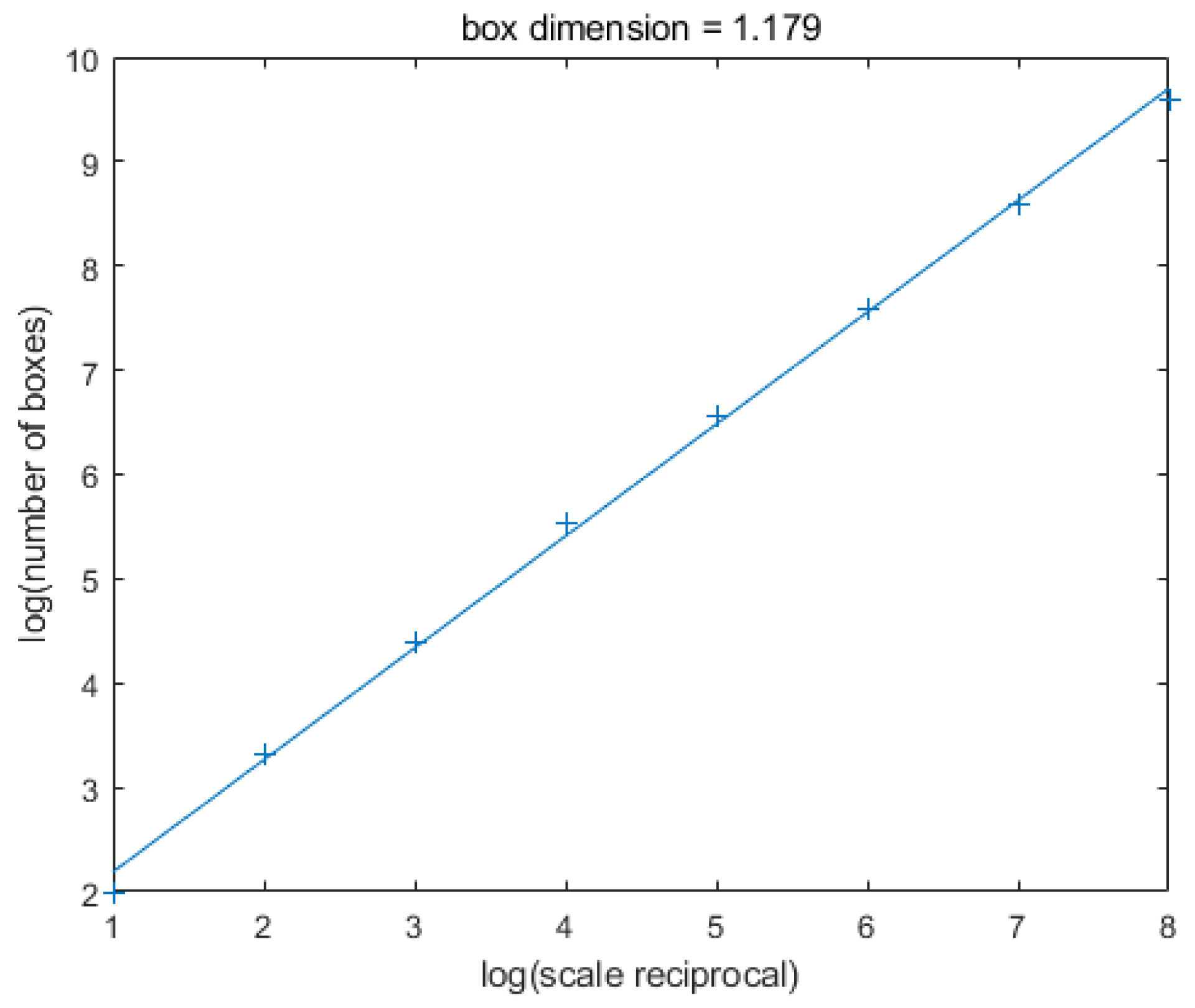
3.2.1. Box Dimension Method
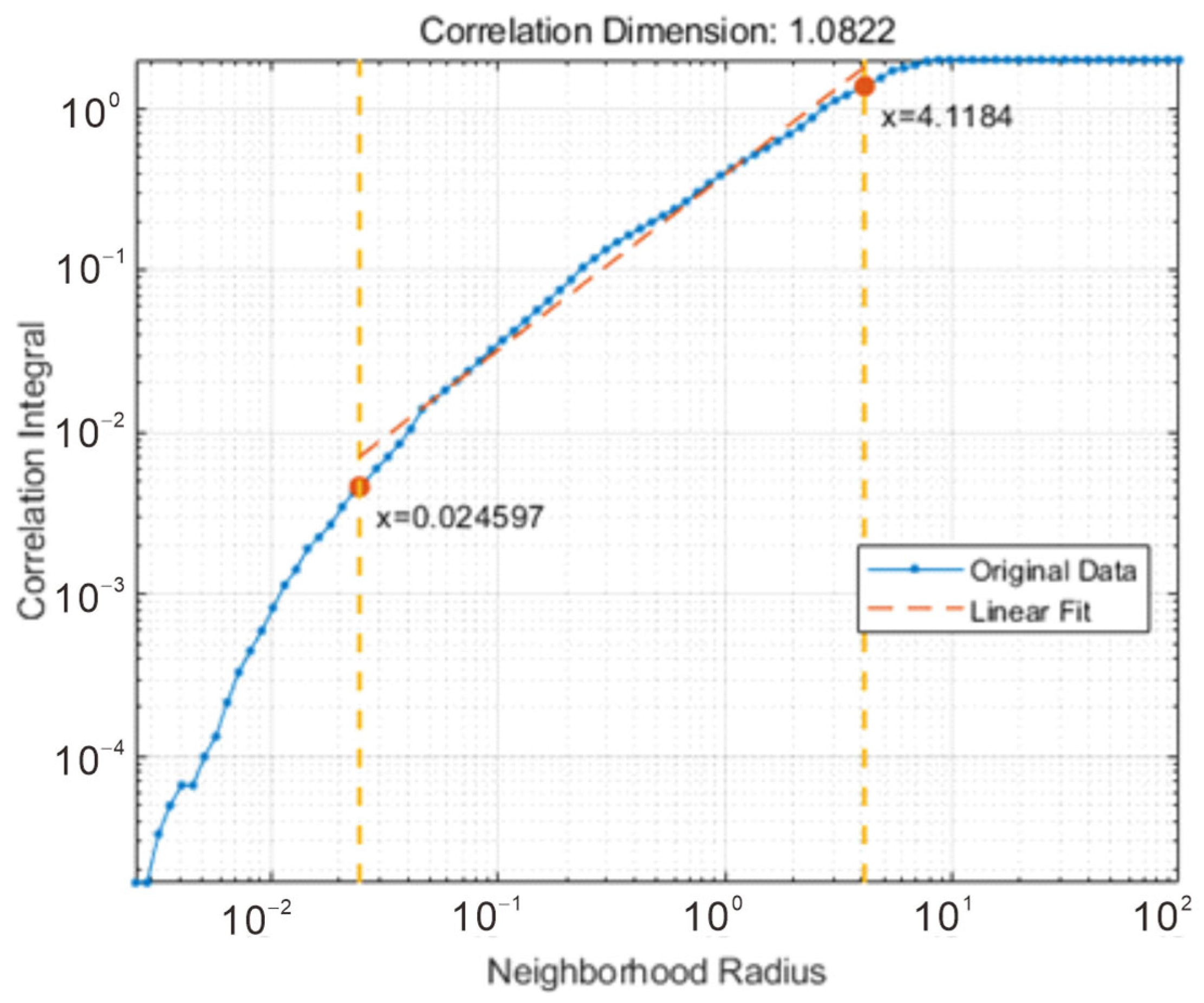
3.2.2. Correlation Dimension Method
3.2.3. Multifractal Calculation Based on Wave Leader Method
4. Results and Analysis
4.1. Heterogeneity Analysis Based on Core Permeability
4.2. Fractal Analysis of Well Logs
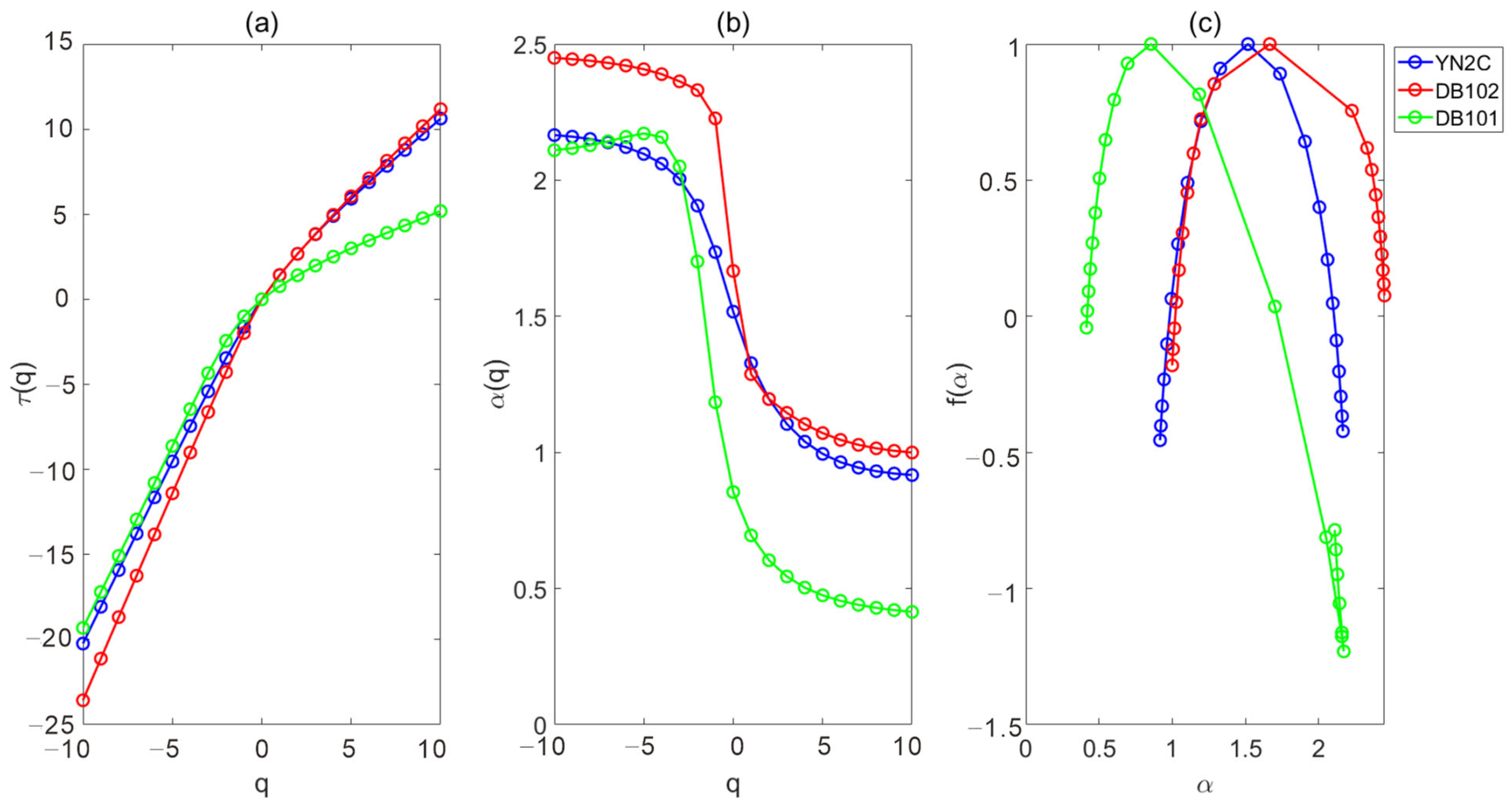
4.3. Correlation Between Heterogeneity and Production
5. Conclusions
- (1)
- In the analysis of core permeability, the heterogeneity of gas layers is small, and that of dry layers is the largest.
- (2)
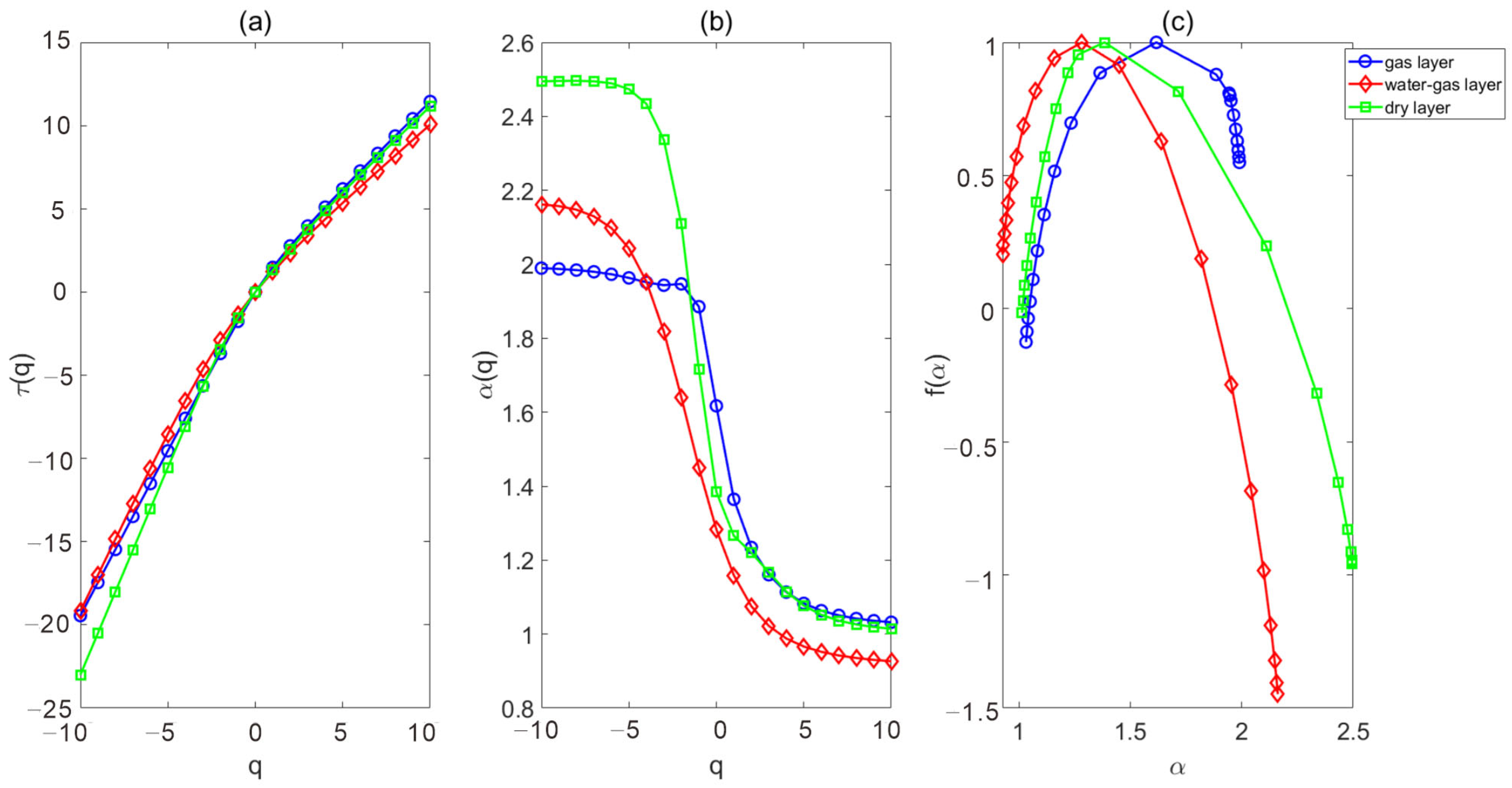
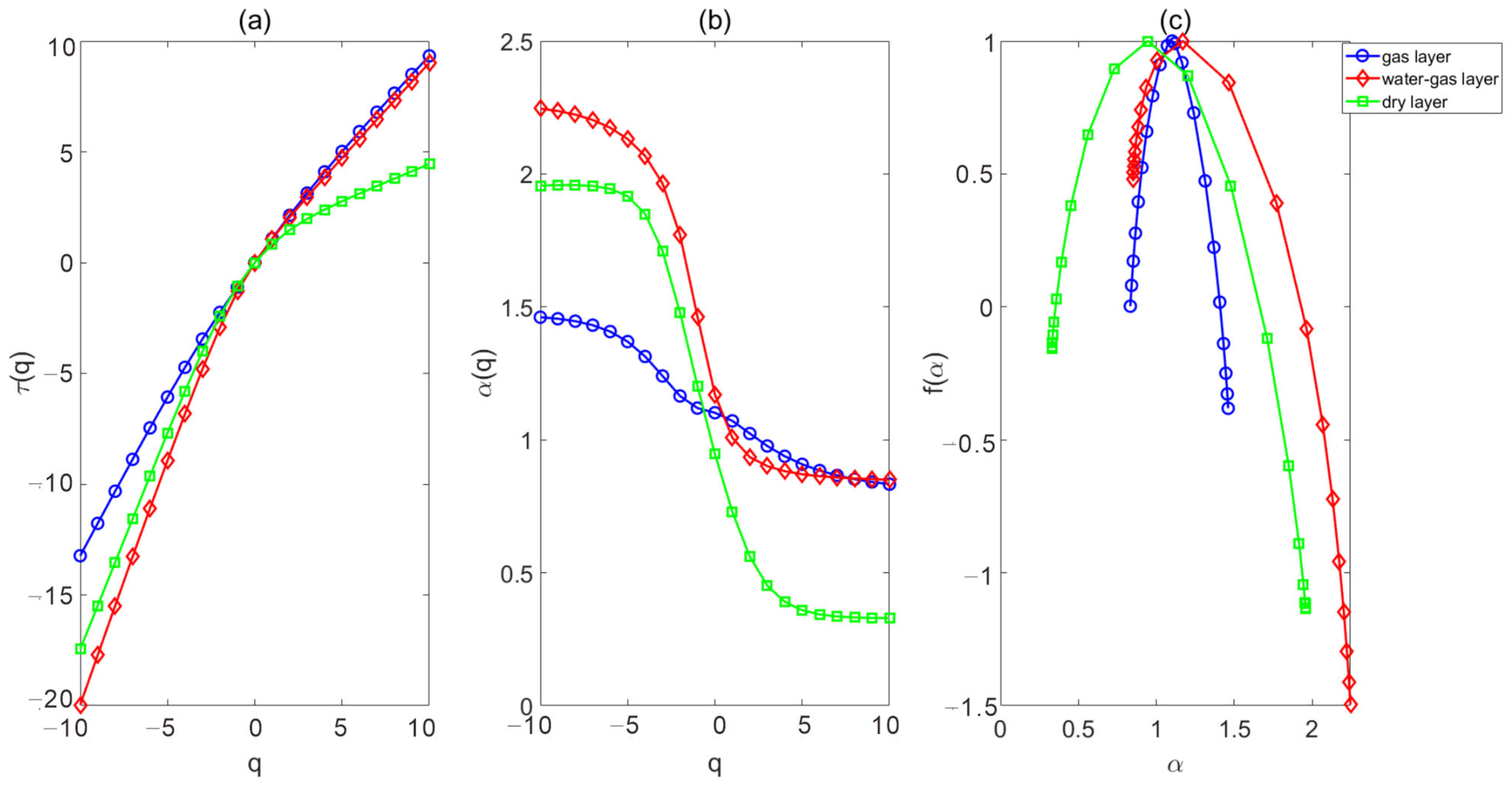
- The box dimension, correlation dimension, and multifractal parameter of gas layers, dry layers, and water–gas layers were calculated using well logs. The fractal dimension of the GR log reflects the intralayer heterogeneity within the layer, while the fractal dimension of the acoustic log indicates microscopic heterogeneity. This analysis also examines the two types of heterogeneity in different reservoirs. The two heterogeneity and gas content results were consistent. The calculation results also have good consistency with the results based on core permeability. Layers with high gas content exhibit lower fractal dimensions and weaker heterogeneity, while the dry layers exhibit a larger fractal dimension and stronger heterogeneity.
- (3)
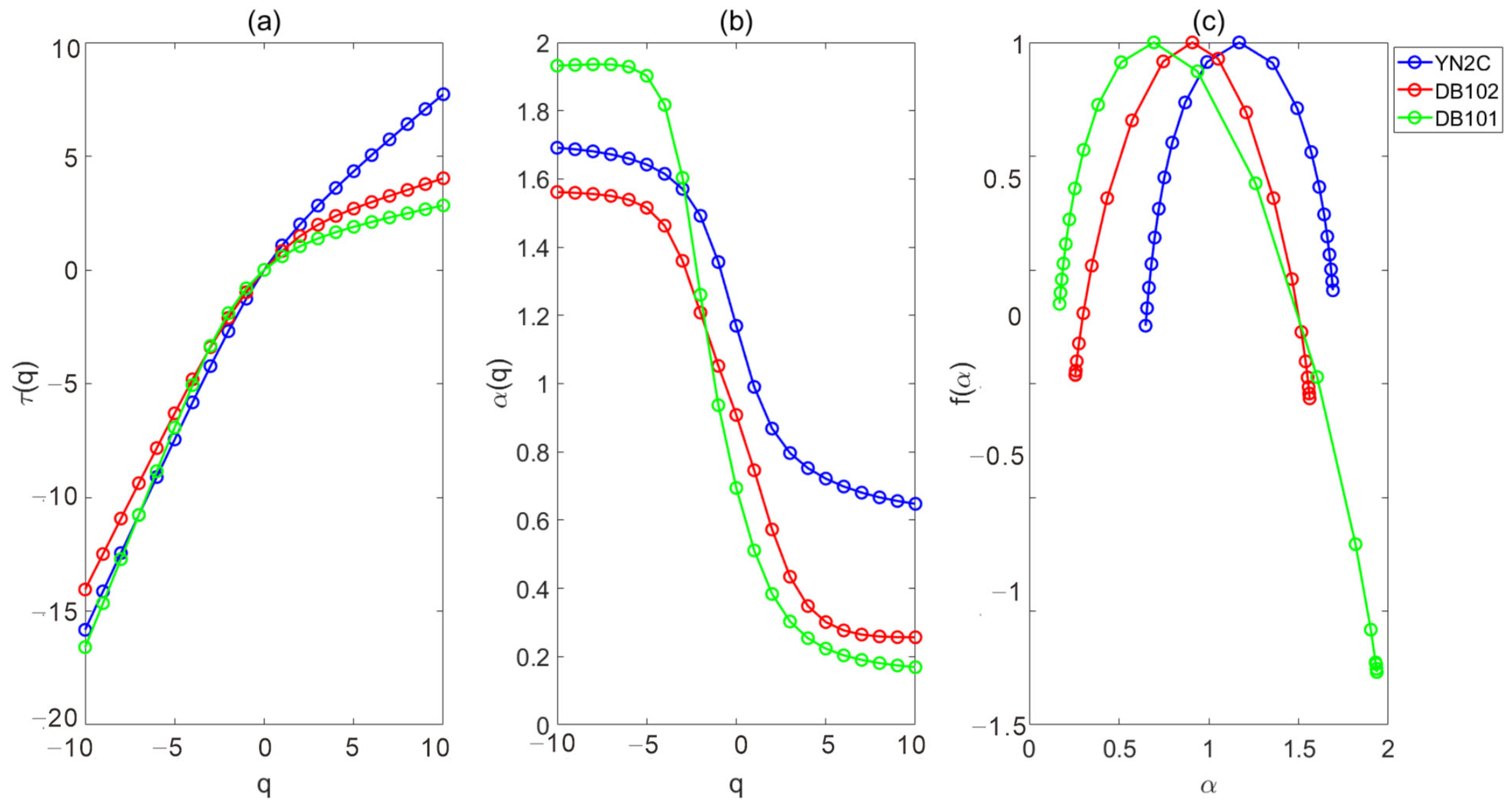
- The fractal dimensions and multifractal parameters of the wells with gas production were calculated using GR and acoustic logs, and the heterogeneity of different wells was analyzed. As a result, it was determined that the weaker the heterogeneity, the higher the production. Therefore, the reservoir heterogeneity could be used as an indicator for production estimation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hong, D.; Cao, J.; Wu, T.; Dang, S.; Hu, W.; Yao, S. Authigenic Clay Minerals and Calcite Dissolution Influence Reservoir Quality in Tight Sandstones: Insights from the Central Junggar Basin, NW China. Energy Geosci. 2020, 1, 8–19. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, H.; Yang, W. New progress and future exploration targets in petroleum geological research of ultra-deep clastic rocks in Kuqa Depression, Tarim Basin, NW China. Pet. Explor. Dev. 2025, 52, 79–94. [Google Scholar] [CrossRef]
- Wang, G.-X.; Wu, W.; Li, Q.; Liu, W.-Q.; Zhou, Y.-S.; Liang, S.-Q.; Sui, Y.-P. Sequence stratigraphy and sedimentary evolution from Late Cretaceous to Quaternary in the Romney 3D seismic area, deep-water Taranaki Basin (New Zealand). Pet. Sci. 2025, 22, 1854–1875. [Google Scholar] [CrossRef]
- Tao, K.; Cao, J.; Chen, X.; Nueraili, Z.; Hu, W.; Shi, C. Deep Hydrocarbons in the Northwestern Junggar Basin (NW China): Geochemistry, Origin, and Implications for the Oil vs. Gas Generation Potential of Post-Mature Saline Lacustrine Source Rocks. Mar. Pet. Geol. 2019, 109, 623–640. [Google Scholar] [CrossRef]
- Mao, Z.; Zeng, L.; Liu, G.; Gao, Z.; Tian, H.; Liao, Q.; Zhang, Y. Fractures and Their Effectiveness in the Deep Jurassic Tight Sandstone Reservoir in the Southern Margin of the Junggar Basin. Pet. Geol. 2020, 41, 1212–1221. [Google Scholar] [CrossRef]
- Lai, J.; Li, D.; Bai, T.; Zhao, F.; Ai, Y.; Liu, H.; Cai, D.; Wang, G.; Chen, K.; Xie, Y. Reservoir Quality Evaluation and Prediction in Ultra-Deep Tight Sandstones in the Kuqa Depression, China. J. Struct. Geol. 2023, 170, 104850. [Google Scholar] [CrossRef]
- Wang, J.Y.; Wang, B.; Hu, Z.Q.; Shang, F.; Liu, D.; Li, Z.; Qiu, Q.; Song, Z.; Hu, Z. Genetic Mechanism of High-Quality Reservoirs in Deep-Ultra-Deep Clastic Rocks: A Case Study of the Permian-Triassic in the Central Junggar Basin, NW China. Pet. Nat. Gas Geol. 2025, 46, 151–166. [Google Scholar]
- Xiao, D.; Lu, S.; Lu, Z.; Huang, W.; Gu, M. Combining Nuclear Magnetic Resonance and Rate-Controlled Porosimetry to Probe the Pore-Throat Structure of Tight Sandstones. Pet. Explor. Dev. 2016, 43, 1049–1059. [Google Scholar] [CrossRef]
- Schmitt, M.; Fernandes, C.P.; Cunha Neto, J.A.B.; Wolf, G.F. Characterization of Pore Systems in Seal Rocks Using Nitrogen Gas Adsorption Combined with Mercury Injection Capillary Pressure Techniques. Mar. Pet. Geol. 2013, 39, 138–149. [Google Scholar] [CrossRef]
- Fitch, P.J.; Lovell, M.A.; Davies, S.J.; Pritchard, T.; Harvey, P.K. An Integrated and Quantitative Approach to Petrophysical Heterogeneity. Mar. Pet. Geol. 2015, 63, 82–96. [Google Scholar] [CrossRef]
- Zheng, C.; Xie, J.; Wang, J.K.; Zhao, X.; Duan, Y.; Sun, Y. Application of Lorenz Coefficient in Reservoir Heterogeneity Evaluation. J. Shandong Univ. Sci. Technol. 2018, 37, 103–110. [Google Scholar] [CrossRef]
- Lake, L.; Jensen, J. A Review of Heterogeneity Measures Used in Reservoir Characterization. Situ 1991, 15, 409–439. [Google Scholar]
- Fitch, P.; Davies, S.; Lovell, M.; Pritchard, T. Reservoir Quality and Reservoir Heterogeneity: Petrophysical Application of the Lorenz Coefficient. Petrophysics 2013, 54, 465–474. [Google Scholar]
- Hosseinzadeh, M.; Tavakoli, V. Analyzing the Impact of Geological Features on Reservoir Heterogeneity Using Heterogeneity Logs: A Case Study of Permian Reservoirs in the Persian Gulf. Geoenergy Sci. Eng. 2024, 237, 212810. [Google Scholar] [CrossRef]
- Farooq, U.; Ahmed, J.; Ali, S.; Pakistan, M.; Siddiqi, F.; Kazmi, S.A.A.; Mushir, K. Heterogeneity in the Petrophysical Properties of Carbonate Reservoirs in Tal Block. In Proceedings of the SPWLA 60th Annual Logging Symposium, The Woodlands, TX, USA, 15–19 June 2019. [Google Scholar] [CrossRef]
- Tavoosi, I.P.; Mehrabi, H.; Rahimpour-Bonab, H.; Ranjbar-Karami, R. Quantitative Analysis of Geological Attributes for Reservoir Heterogeneity Assessment in Carbonate Sequences; A Case from Permian–Triassic Reservoirs of the Persian Gulf. J. Pet. Sci. Eng. 2021, 200, 108356. [Google Scholar] [CrossRef]
- Davies, A.; Cowliff, L.; Simmons, M.D. A Method for Fine-Scale Vertical Heterogeneity Quantification from Well Data and Its Application to Siliciclastic Reservoirs of the UKCS. Mar. Pet. Geol. 2023, 149, 106077. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman: San Francisco, CA, USA, 1982. [Google Scholar]
- Ghanbarian, B.; Hunt, A.G. Fractals: Concepts and Applications in Geosciences; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Jafari, A.; Babadagli, T. Relationship between Percolation–Fractal Properties and Permeability of 2-D Fracture Networks. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2013, 60, 353–362. [Google Scholar] [CrossRef]
- Pia, G.; Sanna, U. An Intermingled Fractal Units Model to Evaluate Pore Size Distribution Influence on Thermal Conductivity Values in Porous Materials. Appl. Therm. Eng. 2014, 65, 330–336. [Google Scholar] [CrossRef]
- Karimpouli, S.; Tahmasebi, P. 3D Multi-Fractal Analysis of Porous Media Using 3D Digital Images: Considerations for Heterogeneity Evaluation. Geophys. Prospect. 2019, 67, 1082–1093. [Google Scholar] [CrossRef]
- Billi, A.; Storti, F. Fractal Distribution of Particle Size in Carbonate Cataclastic Rocks from the Core of a Regional Strike-Slip Fault Zone. Tectonophysics 2004, 384, 115–128. [Google Scholar] [CrossRef]
- Xie, S.; Cheng, Q.; Ling, Q.; Li, B.; Bao, Z.; Fan, P. Fractal and Multifractal Analysis of Carbonate Pore-Scale Digital Images of Petroleum Reservoirs. Mar. Pet. Geol. 2010, 27, 476–485. [Google Scholar] [CrossRef]
- Xia, W.; Xi, K.; Xin, H.; Ma, W.; Zhao, H.; Feng, S.; Dan, W. The Influence of Pore Throat Heterogeneity and Fractal Characteristics on Reservoir Quality: A Case Study of Chang 8 Member Tight Sandstones, Ordos Basin. Unconv. Resour. 2025, 5, 100123. [Google Scholar] [CrossRef]
- Liu, H.; Roquete, M.; Kou, S.; Lindqvist, P.-A. Characterization of Rock Heterogeneity and Numerical Verification. Eng. Geol. 2004, 72, 89–119. [Google Scholar] [CrossRef]
- Liu, P.; Yuan, Z.; Li, K. An Improved Capillary Pressure Model Using Fractal Geometry for Coal Rock. J. Pet. Sci. Eng. 2016, 145, 473–481. [Google Scholar] [CrossRef]
- Zhou, Y.; Xu, J.; Lan, Y.; Zi, H.; Cui, Y.; Chen, Q.; You, L.; Fan, X.; Wang, G. New Insights into Pore Fractal Dimension from Mercury Injection Capillary Pressure in Tight Sandstone. Geoenergy Sci. Eng. 2023, 228, 212059. [Google Scholar] [CrossRef]
- Liu, Y.; Pang, X.Q.; Ding, C.; Chen, D.; Li, M. Pore Structure and Fractal Characteristics of Tight Sandstone Reservoirs in Yan 10 Member of Wuqi Area. Sci. Technol. Eng. 2023, 23, 12474–12483. [Google Scholar]
- Peng, J.; Han, H.; Xia, Q.; Li, B. Fractal Characteristic of Microscopic Pore Structure of Tight Sandstone Reservoirs in Kalpintag Formation in Shuntuoguole Area, Tarim Basin. Pet. Res. 2020, 5, 1–17. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Zhang, Q.; Li, C.; Feng, Y.; Wang, Y.; Xue, Y.; Ma, H. Petrophysical Static Rock Typing for Carbonate Reservoirs Based on Mercury Injection Capillary Pressure Curves Using Principal Component Analysis. J. Pet. Sci. Eng. 2019, 181, 106175. [Google Scholar] [CrossRef]
- Wen, H.M. Research on Fractal Well Logging Interpretation Theory and Methods. Ph.D. Thesis, Chengdu University of Technology, Chengdu, China, 2003. [Google Scholar]
- Mou, D.; Wang, Z.W. Fractal Dimension of Well Logging Curves Associated with the Texture of Volcanic Rocks. In Proceedings of the Industrial and Control Engineering. Ind. Control. Eng. 2014, 278–281. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, Z.; Sun, Z.; Cai, J.; Wang, L. Investigation on the Pore Structure and Multifractal Characteristics of Tight Oil Reservoirs Using NMR Measurements: Permian Lucaogou Formation in Jimusaer Sag, Junggar Basin. Mar. Pet. Geol. 2017, 86, 1067–1081. [Google Scholar] [CrossRef]
- Yan, J.-P.; He, X.; Geng, B.; Hu, Q.-H.; Feng, C.-Z.; Kou, X.-P.; Li, X.-W. Nuclear magnetic resonance T2 spectrum multifractal characteristics and pore structure evaluation. Appl. Geophys. 2017, 14, 205–215. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, X.; Cai, J.; Luo, M.; Zhang, J.; Liu, Y.; Rabiei, M.; Li, C. Multifractal Analysis of Pore Structure of Middle Bakken Formation Using Low Temperature N2 Adsorption and NMR Measurements. J. Pet. Sci. Eng. 2019, 176, 312–320. [Google Scholar] [CrossRef]
- Lv, H.; Guo, J.; Gu, B.; Zhu, Z.; Zhang, Z. A Fracture Identification Method Using Fractal Dimension and Singular Spectrum Entropy in Array Acoustic Logging: Insights from the Asmari Formation in the M Oilfield, Iraq. J. Appl. Geophys. 2025, 233, 105631. [Google Scholar] [CrossRef]
- Lozada-Zumaeta, M.; Arizabalo, R.; Ronquillo-Jarillo, G.; Coconi-Morales, E.; Rivera-Recillas, D.; Castrejón-Vácio, F. Distribution of Petrophysical Properties for Sandy-Clayey Reservoirs by Fractal Interpolation. Nonlinear Process. Geophys. 2012, 19, 239–250. [Google Scholar] [CrossRef]
- Partovi, S.M.A.; Sadeghnejad, S. Fractal Parameters and Well-Logs Investigation Using Automated Well-to-Well Correlation. Comput. Geosci. 2017, 103, 59–69. [Google Scholar] [CrossRef]
- López, M.; Aldana, M. Facies Recognition Using Wavelet Based Fractal Analysis and Waveform Classifier at the Oritupano-A Field, Venezuela. Nonlinear Process. Geophys. 2007, 14, 325–335. [Google Scholar] [CrossRef]
- Subhakar, D.; Chandrasekhar, E. Reservoir Characterization Using Multifractal Detrended Fluctuation Analysis of Geophysical Well-Log Data. Stat. Mech. Its Appl. 2016, 445, 57–65. [Google Scholar] [CrossRef]
- Amoura, S.; Gaci, S.; Barbosa, S.; Farfour, M.; Bounif, M. Investigation of Lithological Heterogeneities from Velocity Logs Using EMD-Hölder Technique Combined with Multifractal Analysis and Unsupervised Statistical Methods. J. Pet. Sci. Eng. 2022, 208, 109588. [Google Scholar] [CrossRef]
- Prajapati, R.; Kumar, R.; Singh, U.K. Assessment of Reservoir Heterogeneities and Hydrocarbon Potential Zones Using Wavelet-Based Fractal and Multifractal Analysis of Geophysical Logs of Cambay Basin, India. Mar. Pet. Geol. 2024, 160, 106633. [Google Scholar] [CrossRef]
- Wang, Q.H.; Zhang, R.H.; Yang, X.Z.; Chen, X.; Xiao, D.; Wang, B.; Wu, C.; Yu, H. Major Breakthrough and Geological Significance of Tight Sandstone Gas Ex-ploration in Jurassic Ahe Formation of Dibei Area, Eastern Kuqa Depression. Acta Pet. Sinica. 2022, 43, 1049–1064. [Google Scholar] [CrossRef]
- Zhao, M.J.; Zhang, S.C. Genetic Types and Accumulation Conditions of Natural Gas in Tarim Basin. China Pet. Explor. 2001, 6, 27–31. [Google Scholar]
- Wei, G.; Wang, K.; Zhang, R.; Wang, B.; Yu, C. Structural Diagenesis and High-Quality Reservoir Prediction of Tight Sandstones: A Case Study of the Jurassic Ahe Formation of the Dibei Gas Reservoir, Kuqa Depression, Tarim Basin, NW China. J. Asian Earth Sci. 2022, 239, 105399. [Google Scholar] [CrossRef]
- Yang, Y.-B.; Xiao, W.; Zheng, L.-L.; Lei, Q.-H.; Qin, C.-Z.; He, Y.-A.; Liu, S.-S.; Li, M.; Li, Y.-M.; Zhao, J.-Z.; et al. Pore Throat Structure Heterogeneity and Its Effect on Gas-Phase Seepage Capacity in Tight Sandstone Reservoirs: A Case Study from the Triassic Yanchang Formation, Ordos Basin. Pet. Sci. 2023, 20, 2892–2907. [Google Scholar] [CrossRef]
- Liang, D.G.; Jia, C.Z. Achievements and Prospect Prediction of Natural Gas Exploration in Tarim Basin. Nat. Gas Ind. 1999, 19, 3–12. [Google Scholar]
- Li, D.; Wang, G.; Bie, K.; Lai, J.; Lei, D.-W.; Wang, S.; Qiu, H.-H.; Guo, H.-B.; Zhao, F.; Zhao, X.; et al. Formation Mechanism and Reservoir Quality Evaluation in Tight Sandstones under a Compressional Tectonic Setting: The Jurassic Ahe Formation in Kuqa Depression, Tarim Basin, China. Pet. Sci. 2024, 22, 998–1020. [Google Scholar] [CrossRef]
- Hu, H.; Wang, G.C.; Wang, Y.Z.; Huang, R. Yan’an Oilfield Fuchang Development Unit Chang 2 Heterogeneity Study. J. Hebei GEO Univ. 2024, 47, 34–42. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Measuring the Strangeness of Strange Attractors. Nonlinear Phenom. 1983, 9, 189–208. [Google Scholar] [CrossRef]
- Liao, Z.; Wang, L.; He, Z. Feature Extraction and Classification of Mining Microseismic Signals Based on EEMD and Correlation Dimension. Gold Sci. Technol. 2020, 28, 585–594. [Google Scholar]
- Tan, Z.; Huang, J.; Ye, C. Identification of major turning points in the Chinese stock market: A Bayesian approach based on improved wavelet leader method and approximation techniques. China Manag. Sci. 2018, 26, 12–24. [Google Scholar] [CrossRef]
- Zhang, L.; Li, R.J.; Liu, X.L. Analysis of Stock Market Effectiveness and Risk Detection Based on Wavelet Leader Multifractal Method. Chin. J. Manag. Sci. 2014, 22, 17–26. [Google Scholar]




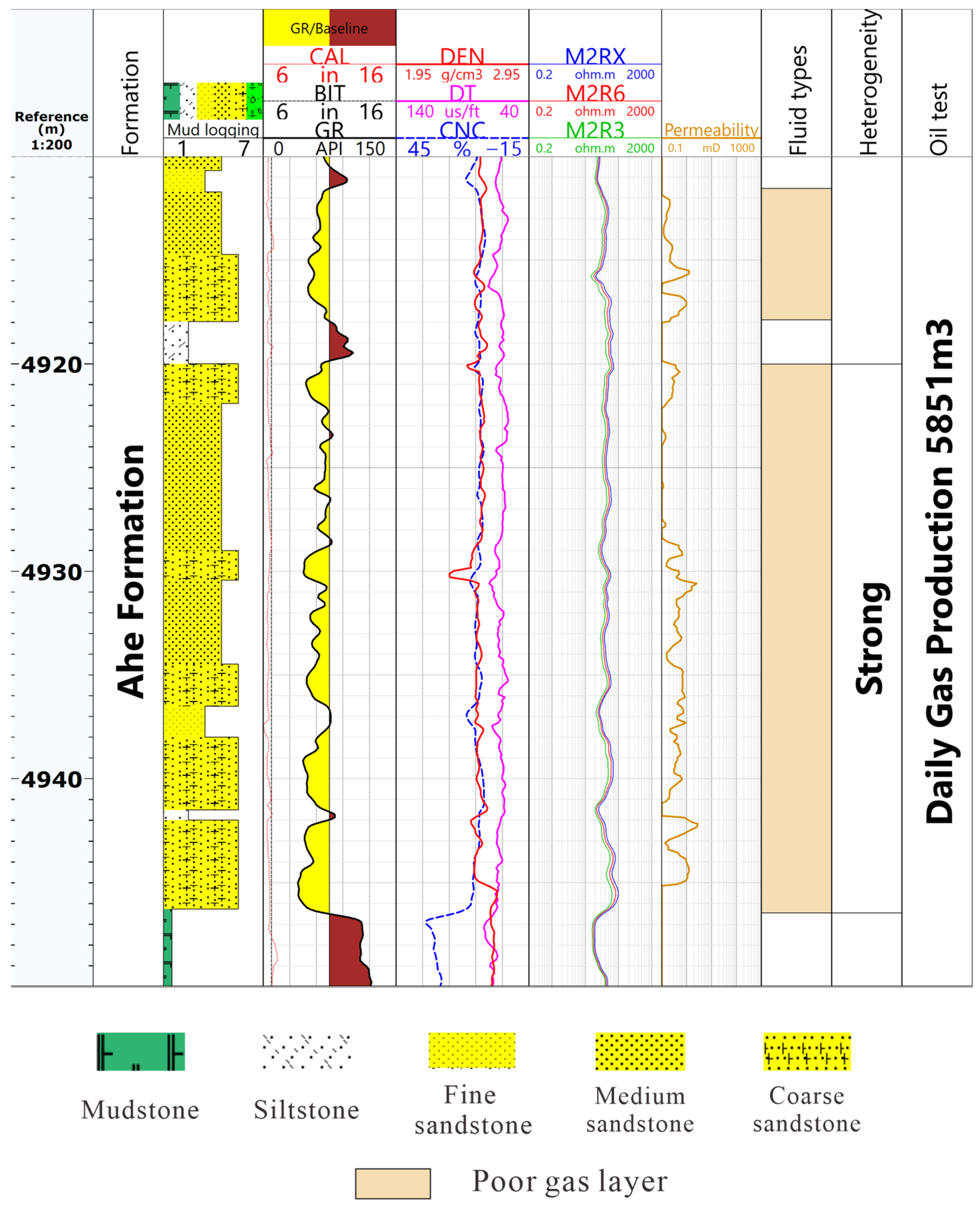
| Wells | YN4 | YN2C | DB101 | DB102 |
|---|---|---|---|---|
| Depth intervals (m) | 285 | 32 | 297 | 284 |
| Average core permeability (mD) | 0.704 | 0.44 | / | 0.04 |
| Oil test (m3/day) | / | 67,320 (gas) | 5851 (gas) | 16,328 (gas) |
| Dry Layer _1 | Water–Gas Layer | Dry Layer _2 | Gas Layer _1 | Gas Layer _2 | |
|---|---|---|---|---|---|
| Wells | YN4 | YN4 | YN4 | YN2C | YN2C |
| Thickness (m) | 10.5 | 5.5 | 8.5 | 5.9 | 7.1 |
| Number of data | 101 | 44 | 88 | 57 | 70 |
| MN (mD) | 0.57 | 1.38 | 0.61 | 0.65 | 0.26 |
| MAX (mD) | 11.9 | 9.07 | 5.61 | 3.09 | 1.81 |
| SD | 1.51 | 1.65 | 0.80 | 0.68 | 0.29 |
| TK | 20.84 | 6.56 | 8.93 | 4.71 | 6.84 |
| CV | 2.65 | 1.19 | 1.32 | 1.04 | 1.11 |
| Heterogeneity | Strong | Moderate | Strong | Weak | Weak |
| Dry Layer _1 | Water–Gas Layer | Dry Layer _2 | Gas Layer _1 | Gas Layer _2 | |
|---|---|---|---|---|---|
| Wells | YN4 | YN4 | YN4 | YN2C | YN2C |
| Thickness (m) | 10.5 | 5.5 | 8.5 | 5.9 | 7.1 |
| Box dimension | 1.179 | 1.138 | 1.208 | 1.082 | 1.081 |
| Correlation dimension | 1.401 | 1.365 | 1.368 | 0.917 | 1.205 |
| Δα | 1.480 | 1.235 | 1.314 | 0.958 | 1.290 |
| α (−10) | 2.495 | 2.162 | 2.202 | 1.990 | 2.094 |
| α (0) | 1.385 | 1.283 | 1.355 | 1.617 | 1.498 |
| α (10) | 1.015 | 0.927 | 0.888 | 1.032 | 0.805 |
| Heterogeneity | Strong | Moderate | Strong | Weak | Weak |
| Dry Layer _1 | Water–Gas Layer | Dry Layer _2 | Gas Layer _1 | Gas Layer _2 | |
|---|---|---|---|---|---|
| Wells | YN4 | YN4 | YN4 | YN2C | YN2C |
| Thickness (m) | 10.5 | 5.5 | 8.5 | 5.9 | 7.1 |
| Box dimension | 1.158 | 1.081 | 1.173 | 1.108 | 1.140 |
| Correlation dimension | 1.175 | 1.044 | 0.975 | 0.978 | 1.057 |
| Δα | 1.627 | 1.396 | 1.728 | 0.863 | 0.628 |
| α (−10) | 1.956 | 2.246 | 1.791 | 1.825 | 1.461 |
| α (0) | 0.947 | 1.171 | 1.037 | 1.394 | 1.102 |
| α (10) | 0.330 | 0.850 | 0.063 | 0.962 | 0.833 |
| Heterogeneity | Strong | Moderate | Strong | Weak | Weak |
| YN2C | DB102 | DB101 | |
|---|---|---|---|
| Box dimension | 1.228 | 1.232 | 1.334 |
| Correlation dimension | 1.581 | 1.686 | 1.659 |
| Δα | 1.044 | 1.305 | 1.762 |
| α (−10) | 1.691 | 1.562 | 1.932 |
| α (0) | 1.169 | 0.908 | 0.694 |
| α (10) | 0.648 | 0.257 | 0.169 |
| YN2C | DB102 | DB101 | |
|---|---|---|---|
| Box dimension | 1.130 | 1.187 | 1.342 |
| Correlation dimension | 1.137 | 1.079 | 1.799 |
| Δα | 1.248 | 1.450 | 1.695 |
| α (−10) | 2.165 | 2.449 | 2.110 |
| α (0) | 1.517 | 1.667 | 0.855 |
| α (10) | 0.916 | 1.000 | 0.414 |
| YN2C | DB102 | DB101 | |
|---|---|---|---|
| Δα based on GR logs | 1.044 | 1.305 | 1.763 |
| Δα based on acoustic logs | 1.248 | 1.450 | 1.695 |
| Oil test (m3/day) | 67,320 (gas) | 16,328 (gas) | 5851 (gas) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, P.; Lv, Q.; Xin, Y.; Wu, N. Heterogeneity of Deep Tight Sandstone Reservoirs Using Fractal and Multifractal Analysis Based on Well Logs and Its Correlation with Gas Production. Fractal Fract. 2025, 9, 431. https://doi.org/10.3390/fractalfract9070431
Zhao P, Lv Q, Xin Y, Wu N. Heterogeneity of Deep Tight Sandstone Reservoirs Using Fractal and Multifractal Analysis Based on Well Logs and Its Correlation with Gas Production. Fractal and Fractional. 2025; 9(7):431. https://doi.org/10.3390/fractalfract9070431
Chicago/Turabian StyleZhao, Peiqiang, Qiran Lv, Yi Xin, and Ning Wu. 2025. "Heterogeneity of Deep Tight Sandstone Reservoirs Using Fractal and Multifractal Analysis Based on Well Logs and Its Correlation with Gas Production" Fractal and Fractional 9, no. 7: 431. https://doi.org/10.3390/fractalfract9070431
APA StyleZhao, P., Lv, Q., Xin, Y., & Wu, N. (2025). Heterogeneity of Deep Tight Sandstone Reservoirs Using Fractal and Multifractal Analysis Based on Well Logs and Its Correlation with Gas Production. Fractal and Fractional, 9(7), 431. https://doi.org/10.3390/fractalfract9070431






