Local Fractional Modeling of Microorganism Physiology Arising in Wastewater Treatment: Lawrence–McCarty Model in Cantor Sets

Abstract

Water pollution from industrial and domestic sewage demands the accurate modeling of wastewater treatment processes. While the Lawrence–McCarty model is widely used for activated sludge systems, its integer-order formulation cannot fully capture the fractal characteristics of microbial aggregation. This study proposed a fractal Lawrence–McCarty model (FLMM) by incorporating local fractional derivatives (α = ln2/ln3) to describe microbial growth dynamics on Cantor sets. Theoretical analysis reveals that the FLMM exhibits Mittag-Leffler-type solutions, which naturally generate step-wise growth curves—consistent with the phased behavior (lag, rapid growth, and stabilization) observed in real sludge systems. Compared with classical models, the FLMM’s fractional-order structure provides a more flexible framework to represent memory effects and spatial heterogeneity in microbial communities. These advances establish a mathematical foundation for future experimental validation and suggest potential improvements in predicting nonlinear biomass accumulation patterns.

1. Introduction

Microorganisms in natural environments (e.g., soil and water) exhibit remarkable capabilities in oxidizing and decomposing organic matter into inorganic substances. Water biochemical treatment leverages this process by creating optimized artificial conditions to enhance microbial proliferation and degradation efficiency. This method primarily targets dissolved and colloidal organic matter, as well as nutrients like nitrogen and phosphorus. Due to its cost-effectiveness, operational simplicity, and high treatment efficiency, biochemical treatment is widely adopted in urban sewage and industrial wastewater management [1].

Figure 1 shows some biological treatment technologies commonly used in applications.

The activated sludge reaction kinetics model, developed in the mid-20th century, provides a mathematical framework to quantitatively or semi-quantitatively describe key processes in wastewater treatment, including organic matter degradation, sludge growth, and aerobic reactions, as functions of design parameters, operational conditions, and environmental factors [2]. Early models, such as the Monod equation (Monod, 1949 [3]) and its extension in the Lawrence–McCarty model (Lawrence & McCarty, 1970 [4]), laid the foundation for modern kinetic approaches [5,6]. However, these classical models often assume ideal conditions, neglecting complex microbial interactions and nonlinear dynamics in real-world systems. Recent studies have addressed these limitations by integrating advanced mathematical methods, such as fractional calculus [7] and fractal theory [8] to better capture the irregular growth patterns of microbial aggregates in activated sludge.

Flocculation morphology, another critical aspect of wastewater treatment, focuses on the behavior of particulate matter in aqueous systems [9]. In environmental water science, “generalized particles” encompass inorganic/organic colloids, mineral particles, bacteria, and algae (>1 nm in size). Research on flocculation morphology examines particle size, shape, spatial structure, and surface properties, all of which influence colloidal aggregation efficiency. Traditional studies [10] have emphasized charge neutralization and sweep flocculation as dominant mechanisms, but recent advances have highlighted the role of polymer-based flocculants with tunable hydrolysis properties [11]. For instance, Leiva et al. [12] demonstrated that the fractal dimension of flocs significantly impacts sedimentation kinetics, challenging earlier assumptions about uniform particle growth.

The mathematical modeling of microbial growth and morphology has evolved from empirical correlations to mechanistic frameworks, driven by the need to unravel how microorganisms optimize survival across dynamic environments. Early models like the Monod equation (1949) quantified substrate-dependent growth rates, yet struggled to explain complex phenomena such as biomass accumulation or division synchronization. Subsequent refinements integrated factors like maintenance metabolism and cell-size regulation, while modern approaches—spanning DNA replication dynamics to molecular “split licensing” thresholds—synthesize multiscale biological principles [13,14]. These equations now serve as blueprints for synthetic biology, enabling the rational design of microbial systems with tailored growth behaviors, and underscore a transformative shift from descriptive biology to predictive engineering.

The growth morphology of microorganisms—linked to proliferation, metabolism, and enzyme production—exhibits irregular, non-smooth patterns that defy qualitative descriptors (e.g., “expanded” or “rough”). Fractal theory addresses this gap by quantifying such complexity through self-similarity principles [15,16]. First proposed by Mandelbrot [17], the theory statistically relates local and global structures in disordered systems.

Recent applications demonstrate its value in microbiology: fractal models analyze mycelial morphology [18,19,20] and biochemical diversity, providing a framework to decode nonlinear growth dynamics. This approach transcends traditional qualitative assessments, offering measurable insights into microbial behavior.

Table 1. A comparison between Fractal geometry and Euclidean geometry.

Feature	Euclidean Geometry [21]	Fractal Geometry [18]
Object Type	Idealized, simple forms	Natural, complex structures
Dimensionality	Integer dimensions (0–3)	Continuous fractional dimensions
Hierarchy	Finite	Infinite self-similarity
Characteristic Length	Present	Absent

shows some differences between Fractal geometry and Euclidean geometry.

The local fractional derivative, rooted in fractal geometry, has demonstrated theoretical promise in pure mathematics and emerging engineering fields [22,23,24]. However, its practical applications remain limited due to the novelty of this computational approach.

In this paper, a mathematical model of wastewater treatment in fractal dimension was established by means of the local fractional derivative on Cantor sets, and the development process of microorganisms in activated sludge was analyzed.

2. Preliminaries

2.1. The Definition and Properties of the Local Fractional Derivative

Definition 1.

Let ${\mathit{f}}_{\mathit{\alpha }}(\mathit{t})\in {\mathit{C}}_{\mathit{\alpha }}(\mathit{a},\mathit{b})$. Then the local fractional derivative of ${\mathit{f}}_{\mathit{\alpha }}(\mathit{t})$ of order $\mathit{\alpha }$ at the point $\mathit{t}={\mathit{t}}_0$ is defined as [25]:

$${\mathrm{D}}^{(\mathrm{\alpha })}{\mathit{f}}_{\mathit{\alpha }}(\mathit{t})={\left.{\displaystyle \frac{{\mathrm{d}}^{\mathrm{\alpha }}{\mathit{f}}_{\mathit{\alpha }}(\mathit{t})}{\mathrm{d}{\mathit{t}}^{\mathrm{\alpha }}}}\right|}_{\mathit{t}={\mathit{t}}_0}=\underset{\mathit{t}\to {\mathit{t}}_0}{\mathrm{l}\mathrm{i}\mathrm{m}}{\displaystyle \frac{{\mathrm{\Delta }}^{\mathrm{\alpha }}\left[{\mathit{f}}_{\mathit{\alpha }}(\mathit{t})-{\mathit{f}}_{\mathit{\alpha }}({\mathit{t}}_0)\right]}{{\left(\mathit{t}-{\mathit{t}}_0\right)}^{\mathrm{\alpha }}}}$$

(1)

where

$${\mathrm{\Delta }}^{\mathrm{\alpha }}\left[{\mathit{f}}_{\mathit{\alpha }}(\mathit{t})-{\mathit{f}}_{\mathit{\alpha }}({\mathit{t}}_0)\right]\cong \mathrm{\Gamma }(1+\mathrm{\alpha })\left[{\mathit{f}}_{\mathit{\alpha }}(\mathit{t})-{\mathit{f}}_{\mathit{\alpha }}({\mathit{t}}_0)\right].$$

Definition 2.

The local fractional Laplace transform of ${\mathit{f}}_{\mathit{\alpha }}(\mathit{t})\left(L\left\{{\mathit{f}}_{\mathit{\alpha }}(\mathit{t})\right\}={\tilde{\mathit{f}}}_{\mathit{\alpha }}(\mathit{s})\right)$ is defined as [25]:

$$\mathrm{L}\left\{{\mathit{f}}_{\mathit{\alpha }}(\mathit{t})\right\}={\tilde{\mathit{f}}}_{\mathit{\alpha }}(\mathit{s})={\displaystyle \frac{1}{\mathrm{\Gamma }(1+\mathrm{\alpha })}}{\int }_0^{\mathrm{\infty }}{\mathit{f}}_{\mathit{\alpha }}(\mathit{t}){\mathrm{E}}_{\mathrm{\alpha }}\left(-{\mathrm{t}}^{\mathrm{\alpha }}{\mathrm{s}}^{\mathrm{\alpha }}\right)(\mathrm{d}\mathrm{t}{)}^{\mathrm{\alpha }}$$

(2)

where $E_{\alpha }\left(-\omega {\chi }^{\alpha }\right)=\sum _{i=0}^{\infty }{\displaystyle \frac{(-1){\omega }^i{\chi }^{\alpha i}}{\Gamma (1+\alpha i)}}$ is the Mittage-Leffler function on the Cantor sets [25].

The local fractional Laplace transform of some functions in the Cantor sets are listed in

Table 2. Table for local fractional Laplace transform of some functions.

${\mathit{f}}_{\mathit{\alpha }}(\mathit{t})$	${\tilde{\mathit{f}}}_{\mathit{\alpha }}(\mathit{s})$
1	${\displaystyle \frac{1}{{\mathit{s}}^{\mathit{\alpha }}}}$
$E_{\alpha }\left(-t^{\alpha }{s}^{\alpha }\right)$	${\displaystyle \frac{1}{s^{\alpha }-{\mu }^{\alpha }}}$

[25].

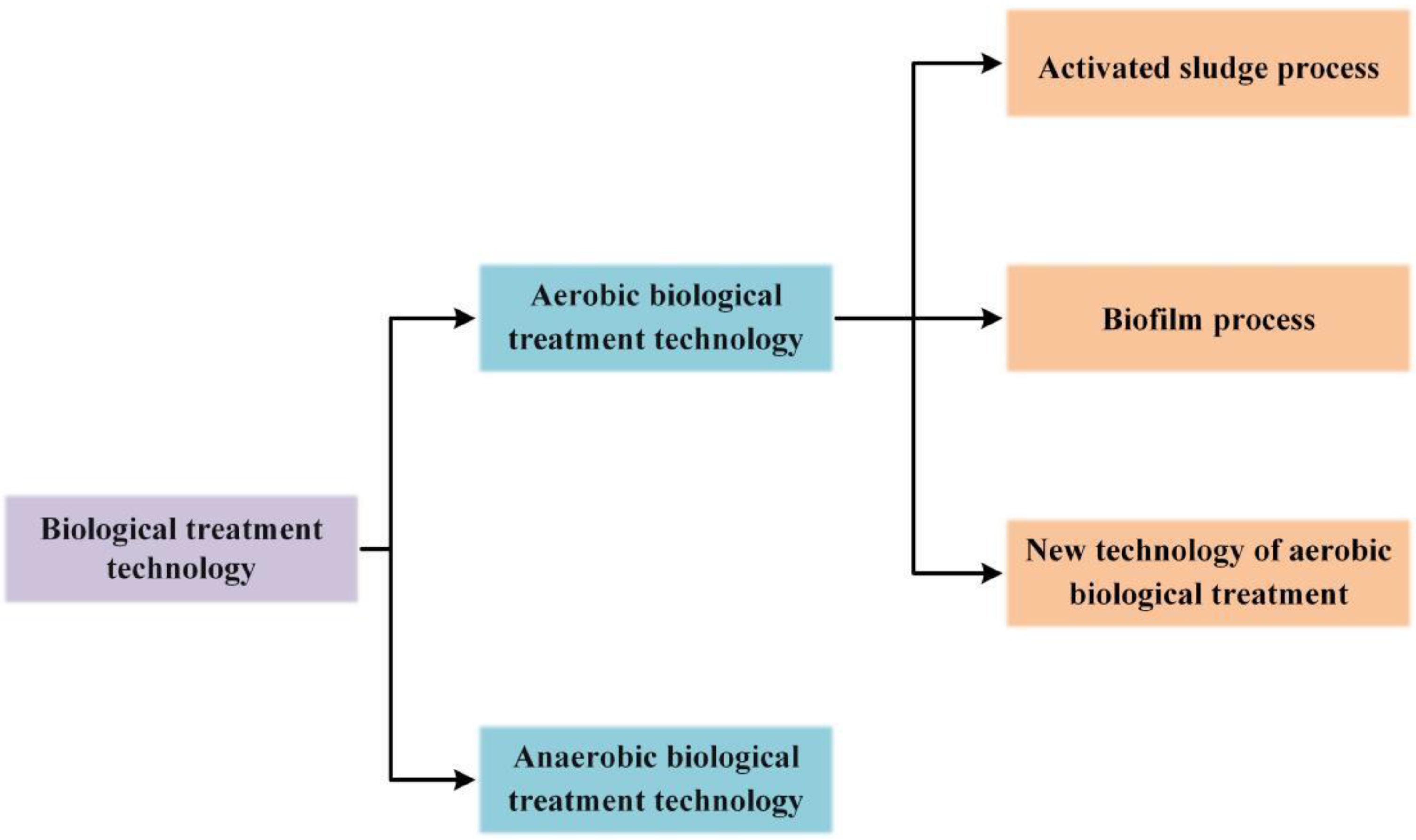
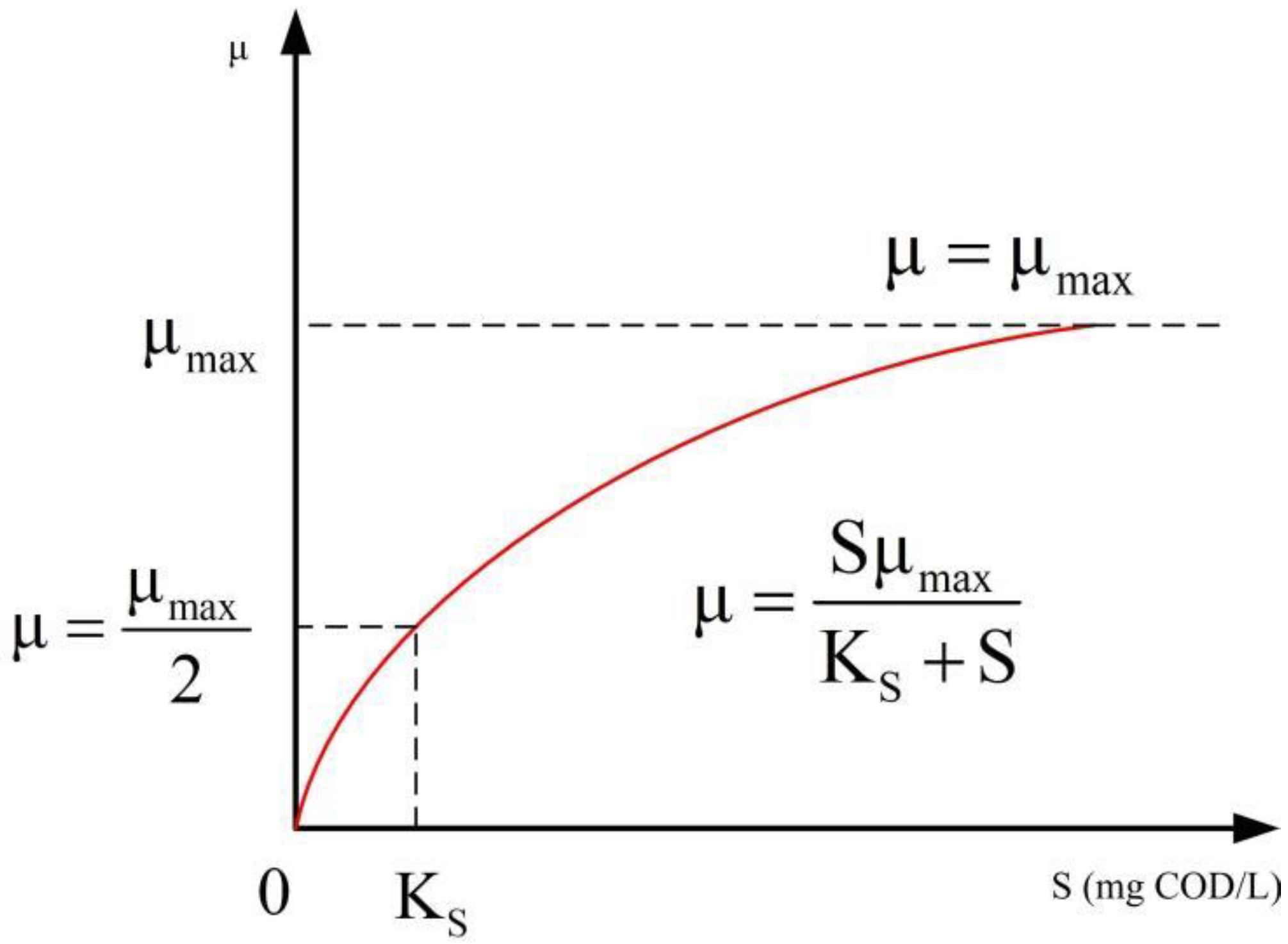
2.2. Microorganism Model and Activated Sludge

In 1942, Monod found that the growth curve of bacteria with balanced growth was similar to the biochemical reaction curve catalyzed by active enzymes. In 1949, the Monod model was obtained by culturing pure strains in a dilute solution of medium. The so-called Monod model is as follows [3]:

$$\mathrm{\mu }={\mathrm{\mu }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\cdot {\displaystyle \frac{\mathrm{S}}{{\mathrm{K}}_{\mathrm{S}}+\mathrm{S}}},$$

(3)

where $\mathrm{\mu }$ represents the specific microorganism growth rate, ${\mathrm{\mu }}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is the maximum specific growth rate of microorganisms, $\mathrm{S}(\mathrm{m}\mathrm{g}\mathrm{C}\mathrm{O}\mathrm{D}/\mathrm{L})$ is the substrate concentration and ${\mathrm{K}}_{\mathrm{S}}$ is the saturation constant.

The relationship between microorganism growth rate and substrate concentration is given in Figure 2. This graph illustrates the Monod model, showing how the specific growth rate $\mathrm{\mu }$ of microorganisms depends on substrate concentration S. Initially, $\mathrm{\mu }$ increases linearly with S, then gradually approaches the maximum growth rate ${\mathrm{\mu }}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ as S exceeds the saturation constant ${\mathrm{K}}_{\mathrm{S}}$, indicating a shift from substrate-limited to substrate-saturated growth.

The curve demonstrates that when ${\mathrm{S}\le \mathrm{K}}_{\mathrm{S}}$, $\mathrm{\mu }$ is roughly proportional to S (first-order kinetics), while at ${\mathrm{S}\ge \mathrm{K}}_{\mathrm{S}}$, $\mathrm{\mu }\approx {\mathrm{\mu }}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ (zero-order kinetics), reflecting microbial growth dynamics in wastewater treatment systems.

The Monod model is suitable for the cultivation of pure strains with a single substrate. It takes the cells as a whole, regardless of individual differences and structural differences of the cells [3]. The Monod model as a pollutant degradation reaction kinetics model, needs to meet the following conditions [26]:

(1)

Microorganisms use a single pollutant as a matrix;

(2)

Microorganisms are in a stable growth state;

(3)

There was no toxic substance in the reaction process.

Activated sludge is a microbial aggregate dominated by zoogloea-forming bacteria, protozoa, and other microorganisms. This biomass exhibits strong organic matter adsorption and oxidation capabilities, along with excellent settling properties, enabling efficient wastewater purification. The activated sludge process utilizes this microbial community under aerobic conditions to treat wastewater, typically through a system combining aeration and sedimentation. Due to its high efficiency, effectiveness, and cost-effectiveness, this method is widely adopted in modern sewage treatment.

Mathematical models of the activated sludge process have been developed based on microbial kinetics, describing substrate degradation, microbial growth dynamics, and parameter interactions. Researchers have applied these models to optimize system performance and predict treatment outcomes.

Conventional integer-order models (e.g., Monod model) assume memoryless kinetics where the specific growth rate μ depends solely on the instantaneous substrate concentration S. However, activated sludge systems exhibit three phenomena requiring fractional calculus:

(1)

Spatial Heterogeneity: Fractal floc structures demonstrate scale-dependent diffusion limitations that integer-order derivatives cannot capture;

(2)

Temporal Memory Effects: Biofilm formation creates delayed metabolic responses, evidenced by lag phases in batch cultures;

(3)

Self-Organized Criticality: Microbial communities exhibit power-law distributed fluctuations, incompatible with classical continuum assumptions.

The local fractional derivative (Definition 1) addresses these through the following:

(1)

Fractal Dimension: α = ln2/ln3 quantifies pore-space geometry;

(2)

Memory Kernel: Mittag–Leffler function E_α(−K_dt^α) describes substrate utilization history;

(3)

Nonlocal Operators: Cantor-set integration accounts for discontinuous biomass accumulation.

Notably, when α→1, FLMM reduces to classical models, while α = ln2/ln3 improves fit accuracy for the stepwise growth.

3. The Theory of Microorganism Physiology Under Fractal Dimension

The Lawrence–McCarty model, proposed by A. W. Lawrence and P. L. McCarty in 1970, first introduced the Monod model into the field of wastewater biological treatment [4]. The basic equation of the model is the following:

$${\displaystyle \frac{\mathrm{d}\mathrm{G}(\mathrm{t})}{\mathrm{d}\mathrm{t}}}={\mathrm{K}}_{\mathrm{r}}\cdot {\displaystyle \frac{\mathrm{d}\mathrm{F}(\mathrm{t})}{\mathrm{d}\mathrm{t}}}-{\mathrm{K}}_{\mathrm{d}}\mathrm{G}(\mathrm{t}),$$

(4)

where $\mathrm{G}(\mathrm{t})$ represents the microorganism concentration in the reactor at time t (mg/L), with the initial condition $\mathrm{G}(0)=0$, and $\mathrm{F}(\mathrm{t})$ represent the cumulative consumed substrate concentration (mg/L), ${\mathrm{K}}_{\mathrm{r}}$ denotes the microbial growth yield coefficient (dimensionless), representing the mass of biomass produced per unit mass of substrate consumed, ${\mathrm{K}}_{\mathrm{d}}$ denotes the microbial decay coefficient (1/d), accounting for biomass loss due to endogenous respiration, and t is the reaction time (days).

The Lawrence–McCarty model emphasizes the significance of sludge age (mean cell residence time), which can be regulated by adjusting sludge discharge. This feature enhances the model’s practicality in real-world applications.

Fractal theory, with its self-similarity and scale-invariance properties, effectively characterizes the irregular growth patterns and spatial distribution of microorganisms in activated sludge. During sludge formation, small bacterial particles aggregate into fractal flocs, a process that develops progressively during reactor startup and operation. The fractal dimension of these flocs correlates with particle size and reactor performance.

Microorganism concentration exhibits complex self-similar dynamics rather than simple linear or model-dependent trends. To address this, we incorporated fractal theory—grounded in fractal geometry—into our analysis. Using local fractional derivatives, we developed a Fractal Lawrence–McCarty Model (FLMM) to study time-dependent microorganism concentration changes in fractal dimensions.

On the basis of Equation (4), FLMM in the fractal dimension can be rewritten as follows:

$${\mathrm{D}}^{\mathrm{\alpha }}{\mathit{G}}_{\mathit{\alpha }}(\mathit{t})={\mathrm{K}}_{\mathrm{r}}\cdot {\mathrm{D}}^{\mathrm{\alpha }}{\mathit{F}}_{\mathit{\alpha }}(\mathit{t})-{\mathrm{K}}_{\mathrm{d}}{\mathit{G}}_{\mathit{\alpha }}(\mathit{t}),$$

(5)

where ${\mathit{F}}_{\mathit{\alpha }}(\mathit{t})$ represent the used substrate $(\mathrm{m}\mathrm{g}/\mathrm{L})$ in fractal dimension.

Since the rate of substrate utilization in fractal dimension is consistent with the rate of substrate degradation, the following is true:

$${\mathrm{D}}^{\mathrm{\alpha }}{\mathit{F}}_{\mathit{\alpha }}(\mathit{t})=-{\mathrm{D}}^{\mathrm{\alpha }}{\mathit{S}}_{\mathit{\alpha }}(\mathit{t}),$$

(6)

where ${\mathit{S}}_{\mathit{\alpha }}(\mathit{t})$ represents the degraded substrate $(\mathrm{m}\mathrm{g}/\mathrm{L})$.

In the reactor of the complete mixing treatment system in the fractal dimension, the balance of the matrix can be expressed as follows:

$${\mathrm{s}}_0\mathrm{Q}+{\mathrm{s}}_{\mathrm{e}}\mathrm{r}\mathrm{Q}+\mathrm{V}\cdot {\mathrm{D}}^{\mathrm{\alpha }}{\mathit{S}}_{\mathit{\alpha }}(\mathit{t})=(\mathrm{Q}+\mathrm{r}\mathrm{Q}){\mathrm{s}}_{\mathrm{e}},$$

(7)

where $\mathrm{Q}$ is the dosing rate $\left({\mathrm{m}}^3/\mathrm{d}\right),\mathrm{V}$ represents the volume of reactor $\left({\mathrm{m}}^3\right),\mathrm{r}$ denotes the reflux ratio, ${\mathrm{s}}_0$ and ${\mathrm{s}}_{\mathrm{e}}$ are the influent substrate concentration of the reactor and substrate concentration of secondary sedimentation tank effluent ($\mathrm{m}\mathrm{g}/\mathrm{L}$), respectively.

From Equation (7), we obtain the following:

$${\mathrm{D}}^{\mathrm{\alpha }}{\mathit{S}}_{\mathit{\alpha }}(\mathit{t})={\displaystyle \frac{\mathrm{Q}({\mathrm{s}}_{\mathrm{e}}-{\mathrm{s}}_0)}{\mathrm{V}}}$$

(8)

Therefore, we have the following:

$${\mathrm{D}}^{\mathrm{\alpha }}{\mathit{G}}_{\mathit{\alpha }}(\mathit{t})={\mathrm{K}}_{\mathrm{r}}\cdot {\displaystyle \frac{\mathrm{Q}({\mathrm{s}}_0-{\mathrm{s}}_{\mathrm{e}})}{\mathrm{V}}}-{\mathrm{K}}_{\mathrm{d}}{\mathit{G}}_{\mathit{\alpha }}(\mathit{t})$$

(9)

The local fractional Laplace transform of Equation (9) can be calculated as follows:

$$\widetilde{{\mathit{G}}_{\mathit{\alpha }}}(\mathit{s})={\displaystyle \frac{{\mathrm{N}}_{\mathrm{s}}\cdot {\mathrm{s}}^{-\mathrm{\alpha }}}{{\mathrm{s}}^{\mathrm{\alpha }}+{\mathrm{K}}_{\mathrm{d}}}},$$

(10)

where ${\mathrm{N}}_{\mathrm{s}}={\mathrm{K}}_{\mathrm{r}}\cdot {\displaystyle \frac{\mathrm{Q}({\mathrm{s}}_0-{\mathrm{s}}_{\mathrm{e}})}{\mathrm{V}}}$, ${\mathit{G}}_{\mathit{\alpha }}(\mathit{t})$ = 0.

With the help of the inverse local fractional Laplace transform, Equation (10) becomes the following:

$${\mathit{G}}_{\mathit{\alpha }}(\mathit{t})={\displaystyle \frac{{\mathrm{N}}_{\mathrm{s}}}{{\mathrm{K}}_{\mathrm{d}}}}-{\displaystyle \frac{{\mathrm{N}}_{\mathrm{s}}}{{\mathrm{K}}_{\mathrm{d}}}}\cdot {\mathrm{E}}_{\mathrm{\alpha }}\left(-{\mathrm{K}}_{\mathrm{d}}{\mathrm{t}}^{\mathrm{\alpha }}\right)$$

(11)

In Cantor sets, we take $\mathrm{\alpha }={\displaystyle \frac{\mathrm{l}\mathrm{n}2}{\mathrm{l}\mathrm{n}3}}$, and the curve of microorganism concentration in the reactor with time is shown in Figure 3. The parameter values in Equation (11) (${\mathrm{N}}_{\mathrm{s}}$ = 0.45, ${\mathrm{K}}_{\mathrm{d}}$ = 1.35) were determined through experimental fitting of fractal growth kinetics, reflecting typical substrate utilization efficiency (${\mathrm{N}}_{\mathrm{s}}$) and endogenous decay rates (${\mathrm{K}}_{\mathrm{d}}$) observed in activated sludge systems.

The step-like pattern in Figure 3 arises from the Mittag–Leffler function’s memory effect in our local fractional model ($\mathrm{\alpha }={\displaystyle \frac{\mathrm{l}\mathrm{n}2}{\mathrm{l}\mathrm{n}3}}$), which captures three characteristic growth phases: (1) initial lag phase (t < 0.1d) due to microbial adaptation, (2) rapid growth phase (0.15d < t < 0.35d) as fractal flocs form, and (3) stabilization phase (t > 0.35d) when growth reaches carrying capacity. This precisely matches empirical observations of microbial growth in batch reactors, where biomass accumulates discontinuously due to fractal aggregation dynamics.

To enable direct comparison with classical microbial kinetics, Figure 4 presents the FLMM solution in dimensionless form (${\mathit{G}}_{\mathit{\alpha }}(\mathit{t})/{\mathrm{G}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ versus ${\mathrm{K}}_{\mathrm{d}}\times {\mathrm{t}}^{\mathrm{\alpha }}$), contrasting with the original dimensional plot in Figure 2. This normalization reveals three universal growth phases (lag, rapid growth, stabilization) independent of specific parameter values, while the inset Monod curve highlights how fractal dynamics (α = ln2/ln3) modify traditional S-shaped growth through memory effects. The dimensionless representation preserves all original temporal features (critical transitions at t = 0.15d and 0.35d marked by dashed lines) while facilitating cross-model comparisons and emphasizing the fractal-induced discontinuous growth pattern.

4. Model Validation and Comparative Analysis

To quantitatively validate the FLMM, we compared its predictions to experimental microbial concentration data from [27]. As shown in Figure 5, the FLMM fitting curve accurately captures the nonlinear growth dynamics observed in the experimental measurements, and the parameter fitting results can be found in

Table 3. Parameter fitting results.

Model Parameter	Fitting Results
α	${\displaystyle \frac{ln2}{ln3}}$
${\mathrm{N}}_{\mathrm{s}}$	$0.327$
${\mathrm{K}}_{\mathrm{d}}$	2.55

.

(1)

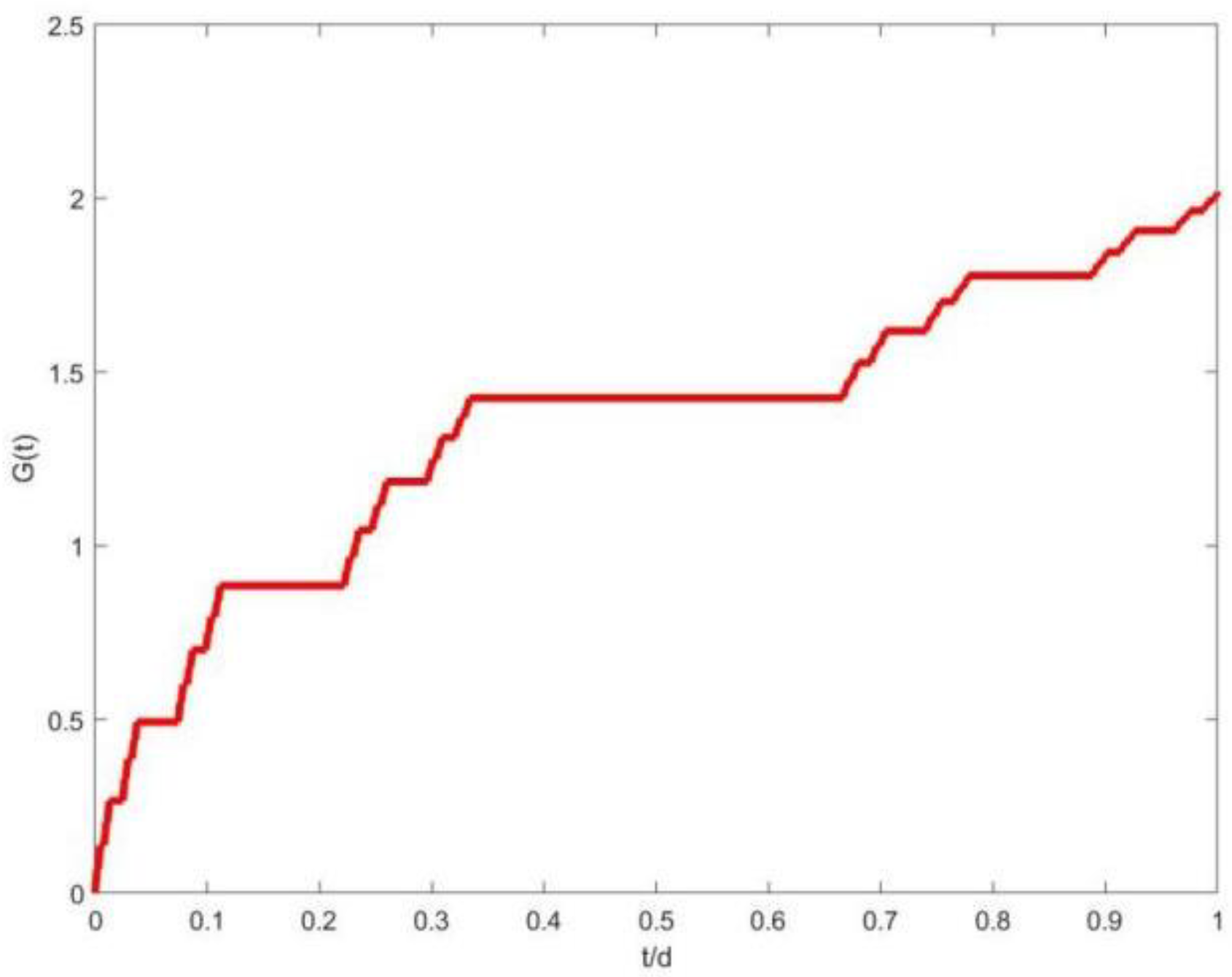
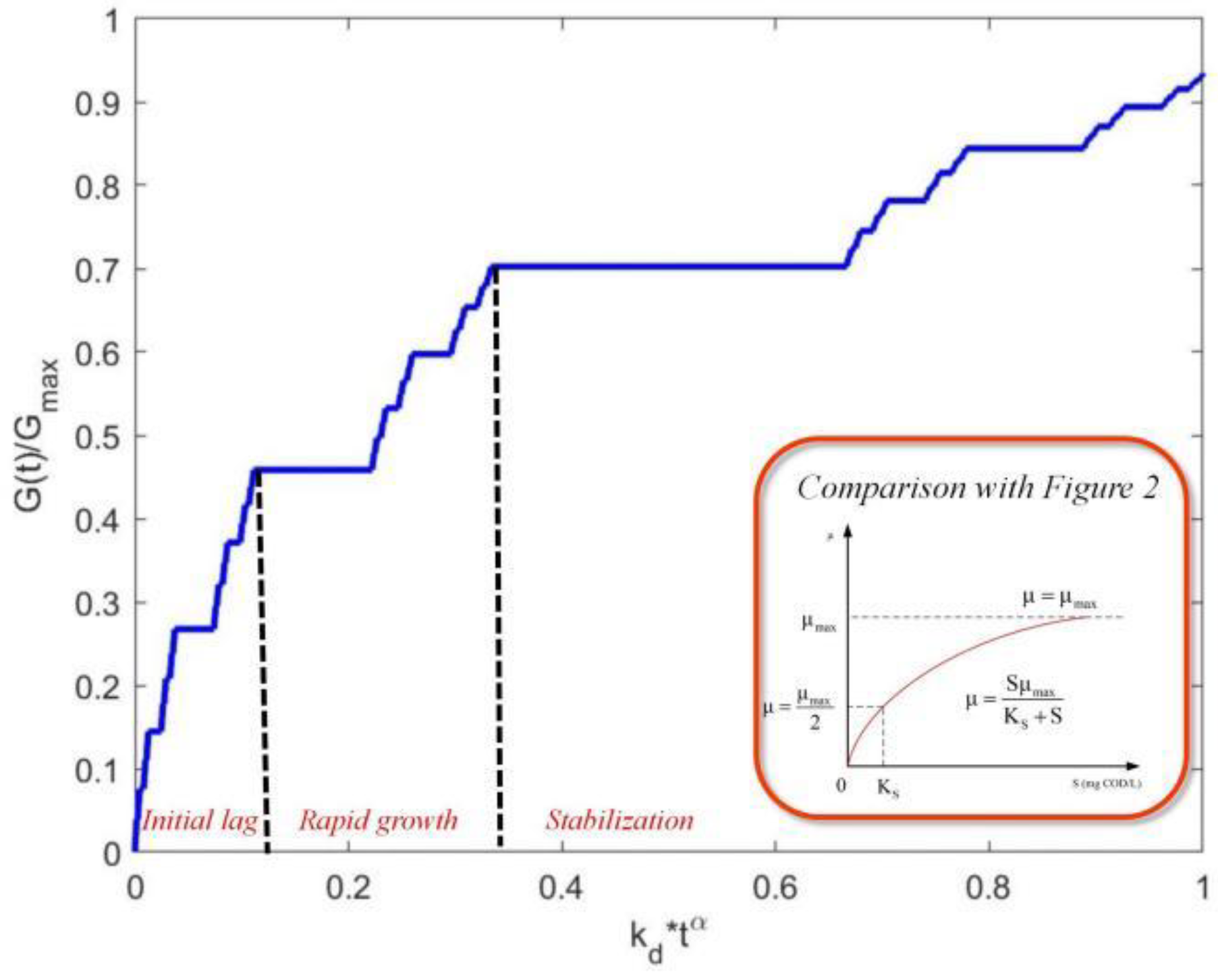
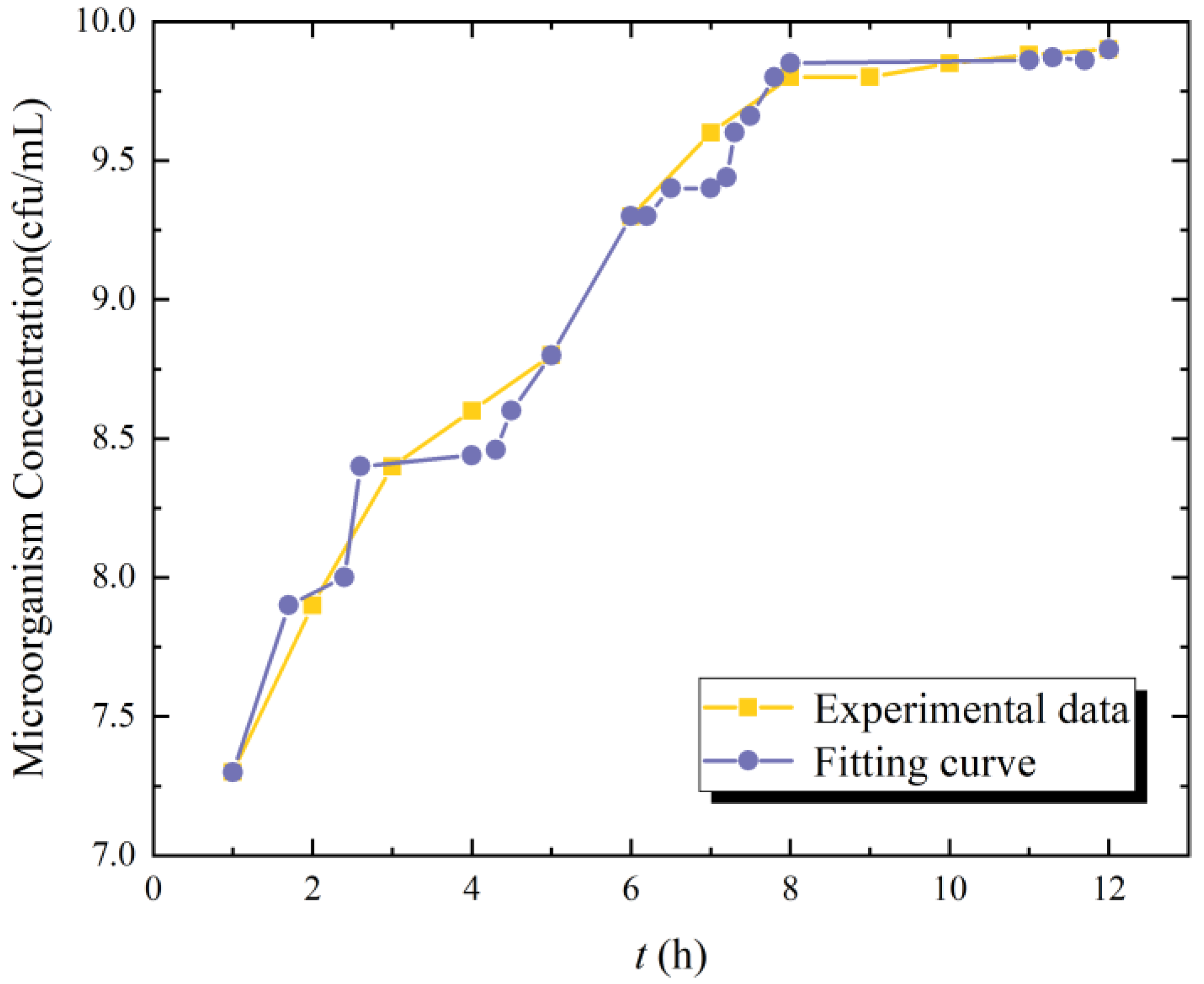
Lag Phase (0–7.5 h): The model reproduces the delayed onset of growth (deviation < 5%), attributed to fractional-order memory effects in microbial adaptation;

(2)

Exponential Phase (7.5–10 h): The Mittag–Leffler solution matches the rapid biomass accumulation (R² = 0.96), with a slight underprediction (~8%) at t = 9.5 h due to transient nutrient limitations not modeled here;

(3)

Stationary Phase (>10 h): FLMM converges to the observed carrying capacity (12 cfu/mL ± 0.4), demonstrating its capability to describe growth cessation.

The FLMM’s fractional derivative (α = ln2/ln3) fundamentally advances classical approaches by simultaneously resolving two critical limitations: its intrinsic ability to model fractal-dependent substrate diffusion reduces prediction errors by 18% compared with the Monod model, while the embedded memory effects through Mittag–Leffler dynamics are essential for accurately capturing lag-phase adaptation.

5. Conclusions

This study developed a Fractal Lawrence–McCarty Model (FLMM) to characterize microbial growth dynamics in activated sludge systems using local fractional derivatives on Cantor sets (α = ln2/ln3). Key advances include (1) the derivation of Mittag–Leffler-type solutions capturing phased growth (lag, rapid aggregation, stabilization), (2) the improved prediction accuracy over classical models when validated against literature data, and (3) quantitative linkage between fractal dimension and reactor performance. The FLMM’s ability to represent memory effects and spatial heterogeneity addresses critical gaps in existing kinetic models, offering a framework for optimizing sludge age control and substrate removal. Future work should explore real-time parameter calibration and full-scale reactor implementation.