Local Fractional Modeling of Microorganism Physiology Arising in Wastewater Treatment: Lawrence–McCarty Model in Cantor Sets
Abstract
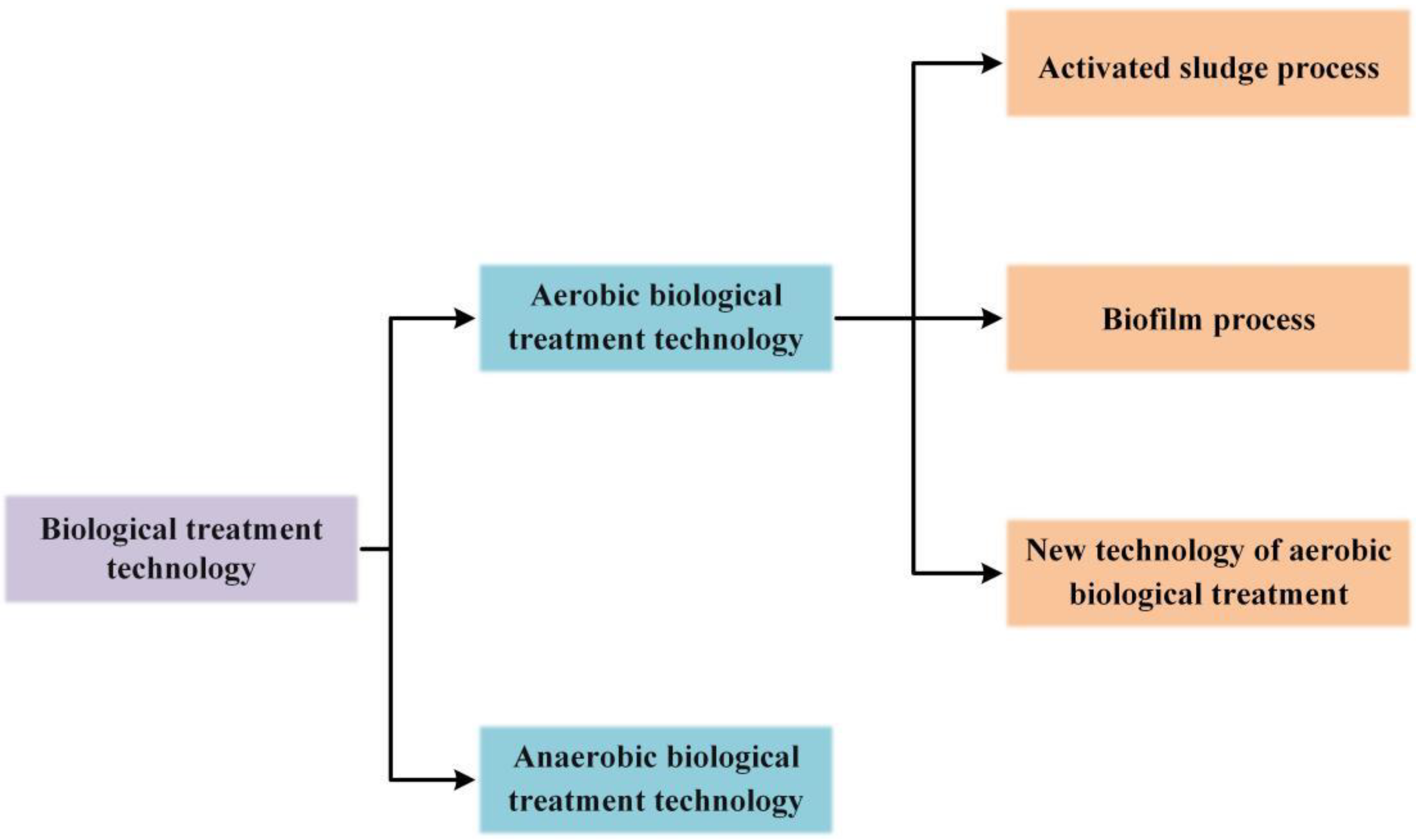
1. Introduction
2. Preliminaries
2.1. The Definition and Properties of the Local Fractional Derivative
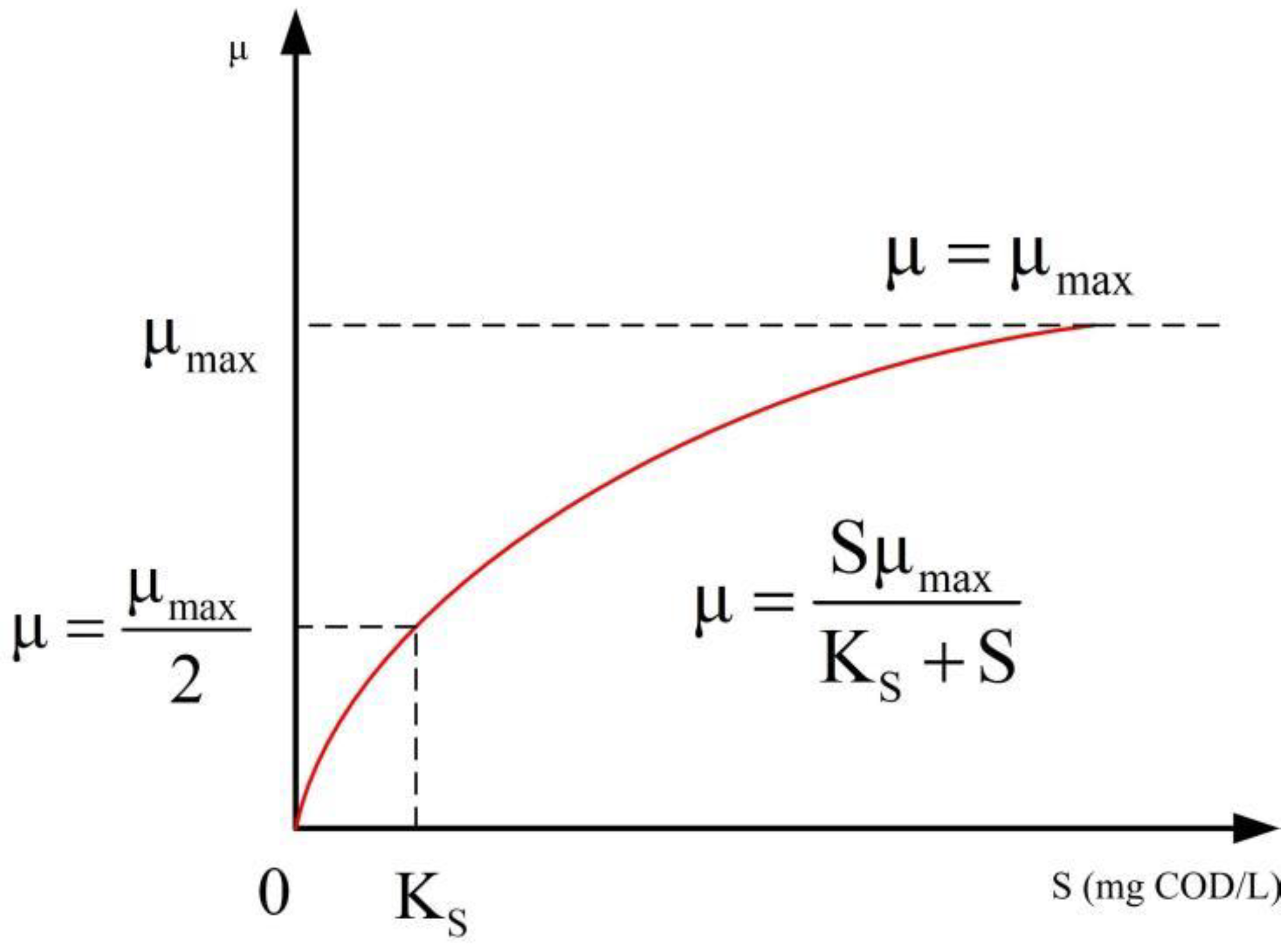
2.2. Microorganism Model and Activated Sludge
- (1)
- Microorganisms use a single pollutant as a matrix;
- (2)
- Microorganisms are in a stable growth state;
- (3)
- There was no toxic substance in the reaction process.
- (1)
- Spatial Heterogeneity: Fractal floc structures demonstrate scale-dependent diffusion limitations that integer-order derivatives cannot capture;
- (2)
- Temporal Memory Effects: Biofilm formation creates delayed metabolic responses, evidenced by lag phases in batch cultures;
- (3)
- Self-Organized Criticality: Microbial communities exhibit power-law distributed fluctuations, incompatible with classical continuum assumptions.
- (1)
- Fractal Dimension: α = ln2/ln3 quantifies pore-space geometry;
- (2)
- Memory Kernel: Mittag–Leffler function Eα(−Kdtα) describes substrate utilization history;
- (3)
- Nonlocal Operators: Cantor-set integration accounts for discontinuous biomass accumulation.
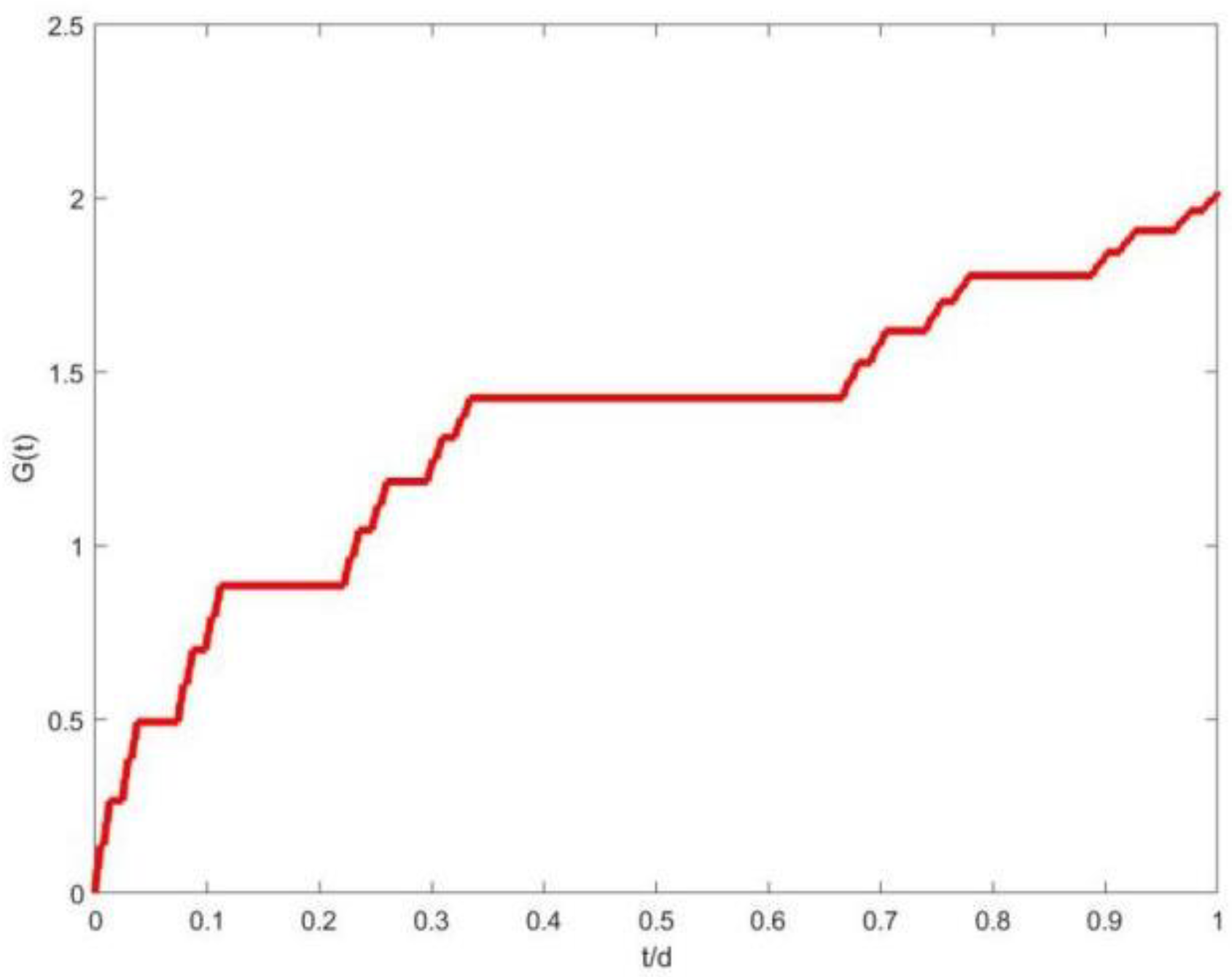
3. The Theory of Microorganism Physiology Under Fractal Dimension
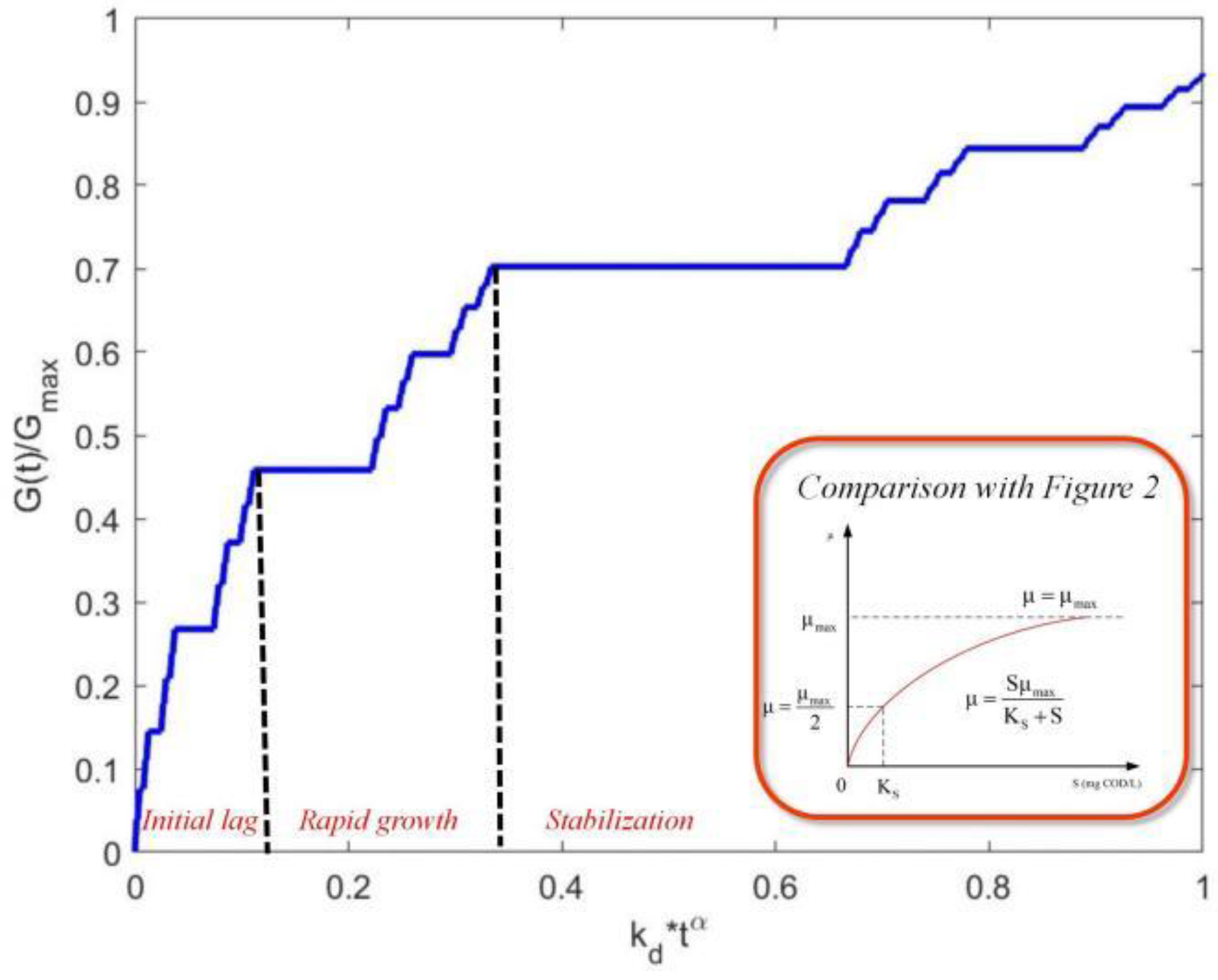
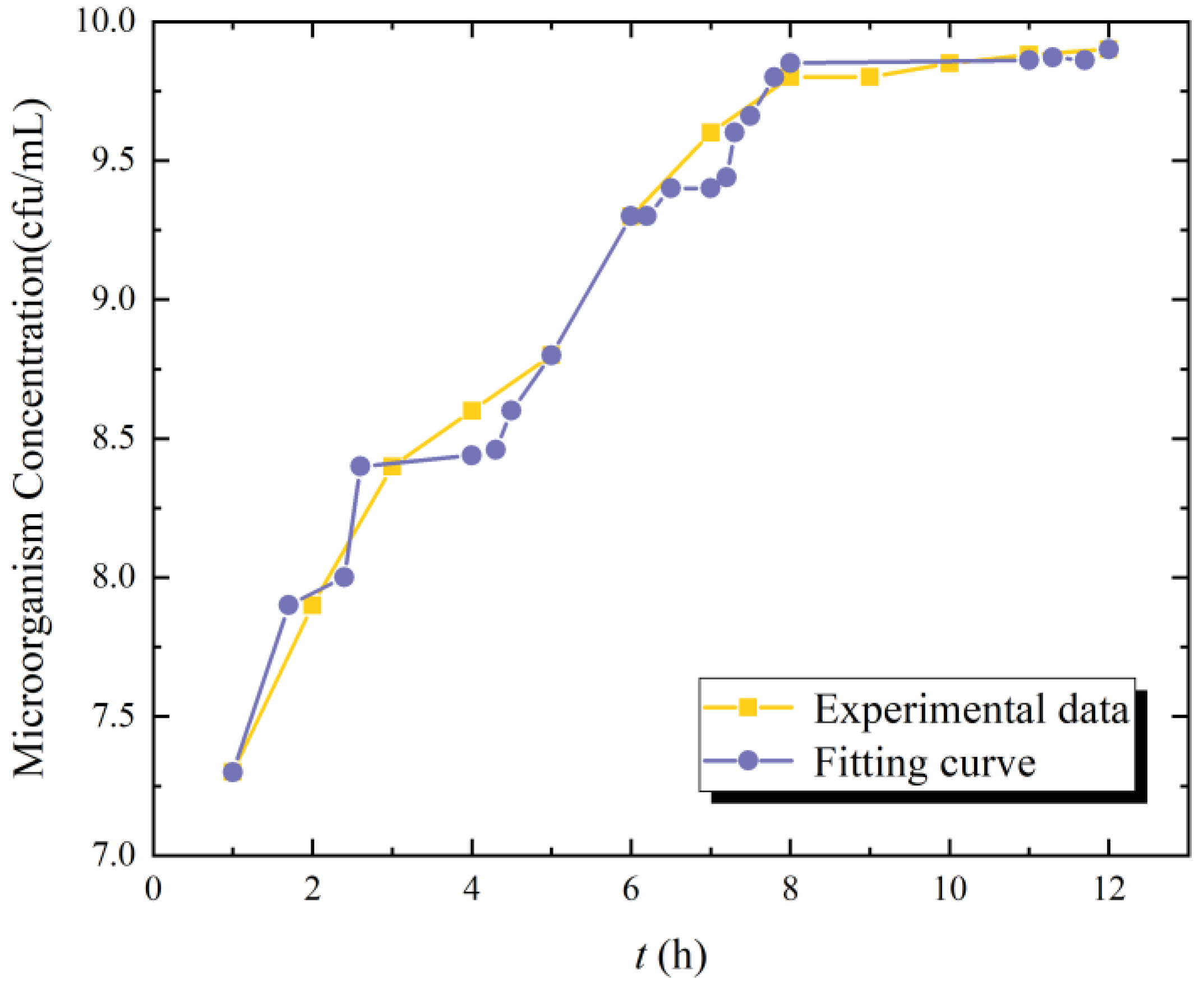
4. Model Validation and Comparative Analysis
- (1)
- Lag Phase (0–7.5 h): The model reproduces the delayed onset of growth (deviation < 5%), attributed to fractional-order memory effects in microbial adaptation;
- (2)
- Exponential Phase (7.5–10 h): The Mittag–Leffler solution matches the rapid biomass accumulation (R2 = 0.96), with a slight underprediction (~8%) at t = 9.5 h due to transient nutrient limitations not modeled here;
- (3)
- Stationary Phase (>10 h): FLMM converges to the observed carrying capacity (12 cfu/mL ± 0.4), demonstrating its capability to describe growth cessation.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liang, M.X.; Lu, X.; Liu, P.; Wu, X.; Zan, F. Tapping the energy potential from wastewater by integrating high-rate activated sludge process with anaerobic membrane bioreactor. J. Clean. Prod. 2022, 333, 130071. [Google Scholar] [CrossRef]
- Yamada, Y.; Kawase, Y. Aerobic composting of waste activated sludge: Kinetic analysis for microbiological reaction and oxygen consumption. Waste Manag. 2006, 26, 49–61. [Google Scholar] [CrossRef] [PubMed]
- Monod, J. The Growth of Bacterial Cultures. Annu. Rev. Microbiol. 1949, 3, 371–394. [Google Scholar] [CrossRef]
- Lawrence, A.W.; McCarty, P.L. Unified basis for biological treatment design and operation. J. Sanit. Eng. Div. 1970, 96, 757–778. [Google Scholar] [CrossRef]
- Singh, V.; Pandey, N.D. A Comparison of Performance of ADM1 and Monod Model Treating Low Strength Wastewater. Mater. Today Proc. 2016, 3, 4157–4162. [Google Scholar] [CrossRef]
- Zhou, S.Q. Theoretical Stoichiometry of Biological Denitrifications. Environ. Technol. 2001, 22, 869–880. [Google Scholar] [CrossRef]
- Tian, X.W.; Xiao, H.; Li, Z.; Su, H.; Ouyang, Q.; Luo, S.; Yu, X. A Fractional Order Creep Damage Model for Microbially Improved Expansive Soils. Front. Earth Sci. 2022, 10, 942844. [Google Scholar]
- Bisht, K.; Klumpp, S.; Banerjee, V.; Marathe, R. Twitching motility of bacteria with type-IV pili: Fractal walks, first passage time, and their consequences on microcolonies. Phys. Rev. E 2017, 96, 52411. [Google Scholar] [CrossRef]
- Wei, Y.; Ding, A.; Dong, L.; Tang, Y.; Yu, F.; Dong, X. Characterisation and coagulation performance of an inorganic coagulant-poly-magnesium-silicate-chloride in treatment of simulated dyeing wastewater. Colloids Surf. A Physicochem. Eng. Asp. 2015, 470, 137–141. [Google Scholar] [CrossRef]
- Raj, P.; Blanco, A.; de la Fuente, E.; Batchelor, W.; Negro, C.; Garnier, G. Microfibrilated cellulose as a model for soft colloid flocculation with polyelectrolytes. Colloids Surf. A Physicochem. Eng. Asp. 2017, 516, 325–335. [Google Scholar] [CrossRef]
- Khalil, N.A.; Lajulliadi, A.F.; Abedin, F.N.J.; Fizal, A.N.S.; Safie, S.I.; Zulkifli, M.; Taweepreda, W.; Hossain, S.; Yahaya, A.N.A. Multifaceted Impact of Lipid Extraction on the Characteristics of Polymer-Based Sewage Sludge towards Sustainable Sludge Management. Polymers 2024, 16, 2646. [Google Scholar] [CrossRef] [PubMed]
- Leiva, W.H.; Toro, N.; Robles, P.; Quezada, G.R.; Salazar, I.; Jeldres, R. Clay Tailings Flocculated in Seawater and Industrial Water: Analysis of Aggregates, Sedimentation, and Supernatant Quality. Polymers 2024, 16, 1441. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Bai, Y.; Jiang, M.; Tokuyasu, T.A.; Huang, X.; Zhong, F.; Wu, Y.; Fu, X.; Kleckner, N.; Hwa, T.; et al. General quantitative relations linking cell growth and the cell cycle in Escherichia coli. Nat. Microbiol. 2020, 5, 995–1001. [Google Scholar] [CrossRef]
- Liu, W.; Cremer, J.; Li, D.; Hwa, T.; Liu, C. An evolutionarily stable strategy to colonize spatially extended habitats. Nature 2019, 575, 664–668. [Google Scholar] [CrossRef]
- Boswell, G.P.; Jacobs, H.; Ritz, K.; Gadd, G.M.; Davidson, F.A. The Development of Fungal Networks in Complex Environments. Bull. Math. Biol. 2007, 69, 605. [Google Scholar] [CrossRef]
- Ben Jacob, E.; Becker, I.; Shapira, Y.; Levine, H. Bacterial linguistic communication and social intelligence. Trends Microbiol. 2004, 12, 366–372. [Google Scholar] [CrossRef]
- Mandelbot, B.B. The Fractal Geanetry of Nature; Freeman WH: San Francisco, CA, USA, 1982; pp. 11–58. [Google Scholar]
- Vorobyov, N.I.; Pishchik, V.N.; Pukhalsky, Y.V.; Sviridova, O.V.; Zhemyakin, S.V.; Semenov, A.M. The Fractal Model of the Microorganism’s Frequencies Spectrum for Determining the Diversity of the Biochemical Processes in Soil. In Information Technologies in the Research of Biodiversity; Bychkov, I., Voronin, V., Eds.; Springer Proceedings in Earth and Environmental Sciences; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Logan, B.E.; Wilkinson, D.B. Fractal dimensions and porosities of Zoogloea ramigera and Saccharomyces cerevisae aggregates. Biotechnol. Bioeng. 1991, 38, 389–396. [Google Scholar] [CrossRef]
- Patankar, D.B.; Liu, T.C. A fractal model for the characterization of mycelial morphology. Biotechnol. Bioeng. 1993, 42, 571–578. [Google Scholar] [CrossRef]
- Miller, R.A. Geometric Algebra: An Introduction with Applications in Euclidean and Conformal Geometry. Master’s Thesis, San Jose State University, San Jose, CA, USA, 2013. [Google Scholar]
- Hashemi, M.S.; Mirzazadeh, M.; Ahmad, H. A reduction technique to solve the (2+1)-dimensional KdV equations with time local fractional derivatives. Opt. Quantum Electron. 2023, 55, 721. [Google Scholar] [CrossRef]
- Yang, X.J.; Machado, J.A.T.; Cattani, C.; Gao, F. On a fractal LC-electric circuit modeled by local fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2017, 47, 200–206. [Google Scholar] [CrossRef]
- Feng, Y.Y.; Yang, X.J.; Liu, J.G.; Chen, Z.Q. Mechanical investigations of local fractional magnetorheological elastomers model on Cantor sets. Phys. A 2023, 621, 128789. [Google Scholar] [CrossRef]
- Yang, X.J.; Baleanu, D.; Srivastava, H.M. Local Fractional Integral Transforms and Their Applications; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Sun, P. Introduction to Activated Sludge Kinetic Model and Numerical Simulation; Chemical Industry Press: Beijing, China, 2009. [Google Scholar]
- Xu, M.Z. Effect of High Voltage Pulsed Electric Field on Microbial Growth and Game Theory; Shanxi Agricultural University: Jinzhong, China, 2021. [Google Scholar]
| Feature | Euclidean Geometry [21] | Fractal Geometry [18] |
|---|---|---|
| Object Type | Idealized, simple forms | Natural, complex structures |
| Dimensionality | Integer dimensions (0–3) | Continuous fractional dimensions |
| Hierarchy | Finite | Infinite self-similarity |
| Characteristic Length | Present | Absent |
| 1 | |
| Model Parameter | Fitting Results |
|---|---|
| α | |
| 2.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Feng, Y.; Xu, X.; Jin, S. Local Fractional Modeling of Microorganism Physiology Arising in Wastewater Treatment: Lawrence–McCarty Model in Cantor Sets. Fractal Fract. 2025, 9, 413. https://doi.org/10.3390/fractalfract9070413
Wang Y, Feng Y, Xu X, Jin S. Local Fractional Modeling of Microorganism Physiology Arising in Wastewater Treatment: Lawrence–McCarty Model in Cantor Sets. Fractal and Fractional. 2025; 9(7):413. https://doi.org/10.3390/fractalfract9070413
Chicago/Turabian StyleWang, Yiming, Yiying Feng, Xiurong Xu, and Shoubo Jin. 2025. "Local Fractional Modeling of Microorganism Physiology Arising in Wastewater Treatment: Lawrence–McCarty Model in Cantor Sets" Fractal and Fractional 9, no. 7: 413. https://doi.org/10.3390/fractalfract9070413
APA StyleWang, Y., Feng, Y., Xu, X., & Jin, S. (2025). Local Fractional Modeling of Microorganism Physiology Arising in Wastewater Treatment: Lawrence–McCarty Model in Cantor Sets. Fractal and Fractional, 9(7), 413. https://doi.org/10.3390/fractalfract9070413






